Оглавление:
Рассмотрим основные вопросы интегрирования функций двух переменных. Полученные определения и результаты могут быть перенесены на функции трех и более переменных.
Двойные интегралы
Двойной интеграл представляет собой обобщение понятия определенного интеграла на случай функций двух переменных.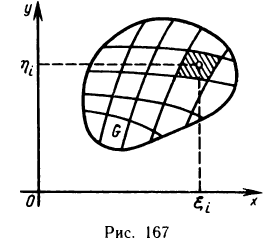
Определение и условия существования двойного интеграла
Пусть G — некоторая замкнутая ограниченная область, a z=f(x, у) — произвольная функция, определенная и ограниченная в этой области.
Предполагается, что граница области G состоит из конечного числа кривых, заданных уравнениями вида y=f(x) или 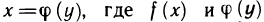 — непрерывные функции. Такой областью, например, является замкнутый многоугольник, граница которого состоит из конечного числа отрезков, представляющих собой графики непрерывных функций вида y=kx+b или х=а. Другой пример — область, ограниченная эллипсом (здесь граница состоит из двух кривых:
— непрерывные функции. Такой областью, например, является замкнутый многоугольник, граница которого состоит из конечного числа отрезков, представляющих собой графики непрерывных функций вида y=kx+b или х=а. Другой пример — область, ограниченная эллипсом (здесь граница состоит из двух кривых: 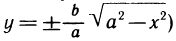 и т. д.
и т. д.
Разобьем область G произвольно на n частей  не имеющих общих внутренних точек, с площадями
не имеющих общих внутренних точек, с площадями 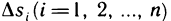 (рис. 167). В каждой части
(рис. 167). В каждой части 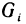 выберем произвольную точку
выберем произвольную точку 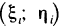 и составим сумму
и составим сумму 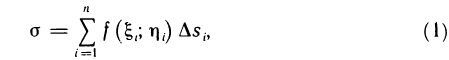
которую назовем интегральной суммой для функции f (х, у) в области G. Назовем диаметром d (G) области G наибольшее расстояние между граничными точками этой области. Обозначим через Я. наибольший из диаметров частичных областей 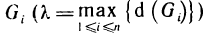
Определение:
Если интегральная сумма (1) при 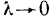 имеет предел, равный I*, то этот предел называется двойным интегралом от функции f (х, у) по области G и обозначается одним из следующих символов:
имеет предел, равный I*, то этот предел называется двойным интегралом от функции f (х, у) по области G и обозначается одним из следующих символов: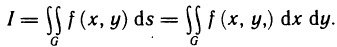
В этом случае функция f (х, у) называется интегрируемой в области G, G — областью интегрирования, х и у — переменными интегрирования, ds (или dx dу) —элементом площади.
Давая определение двойного интеграла, мы предполагаем, что функция f (х, у) ограничена. Как и для функции одной переменной, это условие является необходимым условием интегрируемости. Однако оно не является достаточным, т. е. существуют ограниченные, но не интегрируемые функции. Примером таких функций является функция, определенная на квадрате 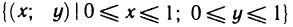 следующим образом:
следующим образом: 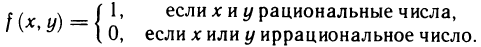
Доказательство неинтегрируемости такой функции непосредственно следует из определения двойного интеграла.
Для нахождения достаточных условий интегрируемости, как и в случае одной переменной, удобно воспользоваться теорией сумм Дарбу, которая полностью переносится на случай двойного интеграла. Аналогично доказательству соответствующей теоремы для определенного интеграла доказывается следующая теорема.
Теорема:
Функция f (x, у), непрерывная в замкнутой ограниченной области G, интегрируема в этой области. Однако не следует считать, что двойной интеграл существует только для непрерывных функций. Имеет место более общая теорема.
Теорема:
Функция f (х, у), ограниченная в замкнутой ограниченной области G и непрерывная в ней всюду, кроме точек, лежащих на конечном числе кривых, являющихся графиками непрерывных функций вида у=f (х) или 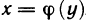 , интегрируема в этой области.
, интегрируема в этой области.
Геометрический смысл двойного интеграла
Пусть в пространстве дано тело Р (рис. 168), ограниченное сверху графиком непрерывной и неотрицательной функции z=f (х, у), которая определена в области G, с боков — цилиндрической поверхностью, направляющей которой служит граница области G, а образующие параллельны оси Oz, и снизу областью G, лежащей в плоскости Оху. Тело такого вида называют криволинейным цилиндром.
Аналогично тому как задача о вычислении площади криволинейной трапеции приводит к установлению геометрического смысла определенного интеграла, так и задача о вычислении объема тела Р приводит к геометрическому толкованию двойного интеграла.
Действительно, в данном случае интегральная сумма (1) представляет собой сумму объемов прямых цилиндров с площадями оснований 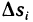 и высотами
и высотами 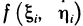 , которую можно принять за приближенное значение объема тела Р:
, которую можно принять за приближенное значение объема тела Р:
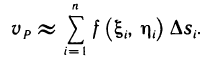
Это приближенное равенство тем точнее, чем мельче разбиение области G на части. При переходе к пределу при 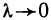 это приближенное равенство становится точным:
это приближенное равенство становится точным: 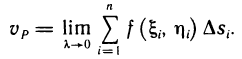

Так как функция f (x, у) интегрируема, то предел интегральной суммы существует и равен двойному интегралу от этой функции по области G. Следовательно, 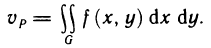
Отсюда следует геометрический смысл двойного интеграла: двойной интеграл от непрерывной, неотрицательной функции равен объему криволинейного цилиндра.
Замечание:
Если положить 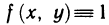 всюду в области G, то непосредственно из определения двойного интеграла получим выражение площади s области G в виде двойного интеграла:
всюду в области G, то непосредственно из определения двойного интеграла получим выражение площади s области G в виде двойного интеграла: 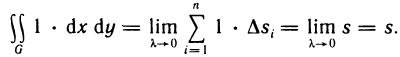
Свойства двойного интеграла
Основные свойства двойного интеграла аналогичны соответствующим свойствам определенного интеграла. Поэтому ограничимся формулировкой этих свойств, не останавливаясь на доказательствах.
1°. Если k — произвольное число и функция f (x, у) интегрируема в области G, то функция kf (х, у) тоже интегрируема в G и 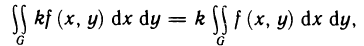 т. е. постоянный множитель можно выносить за знак интеграла.
т. е. постоянный множитель можно выносить за знак интеграла.
2°. Если функции f (х, у) и g (х, у) интегрируемы в области G, то их алгебраическая сумма также интегрируема в этой области и 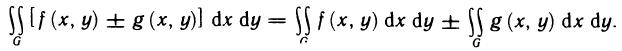
3°. Если область G является объединением областей 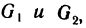 не имеющих общих внутренних точек, в каждой из которых функция f (х, у) интегрируема, то в области G эта функция также интегрируема и
не имеющих общих внутренних точек, в каждой из которых функция f (х, у) интегрируема, то в области G эта функция также интегрируема и 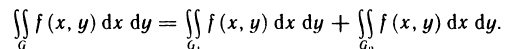
4°. Теорема о среднем. Если функция f(x, у) непрерывна в области G, то в этой области найдется такая точка 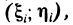 что
что 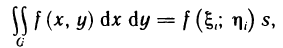
где s — площадь фигуры G.
Итак, рассмотрены определение и основные свойства двойного интеграла, условия существования, выяснен его геометрический смысл. Теперь рассмотрим способы вычисления двойных интегралов.
Сведение двойного интеграла к повторному
Случай прямоугольной области
Сначала рассмотрим двойной интеграл по некоторому прямоугольнику D со сторонами, параллельными осям координат.
Теорема:
Пусть для функции f (х, у) в прямоугольнике 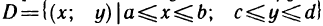 существует двойной интеграл
существует двойной интеграл 
Пусть, далее, для каждого х из отрезка [а, b] существует определенный интеграл 
Тогда существует интеграл 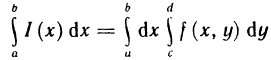
(он называется повторным) и справедливо равенство 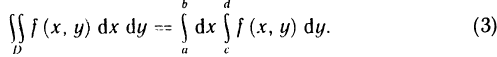
Доказательство:
Разобьем прямоугольник D с помощью точек 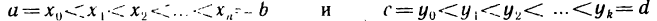 на nk частичных прямоугольников
на nk частичных прямоугольников 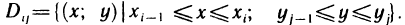 Положим
Положим 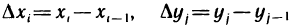 и обозначим через
и обозначим через 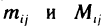 соответственно точную нижнюю и верхнюю грани функции f(x,y) на частичном прямоугольнике
соответственно точную нижнюю и верхнюю грани функции f(x,y) на частичном прямоугольнике 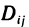 (рис. 169). Тогда всюду на этом прямоугольнике
(рис. 169). Тогда всюду на этом прямоугольнике 
Положим в этом неравенстве 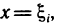 где
где 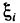 — произвольная точка отрезка
— произвольная точка отрезка 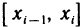 и затем проинтегрируем (4) по у в пределах от
и затем проинтегрируем (4) по у в пределах от 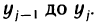 Получим
Получим 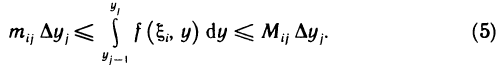
Суммируя (5) по всем j от 1 до k и используя обозначение (2) имеем 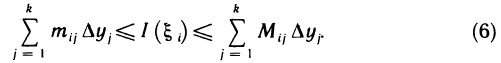
Далее, умножая (6) на 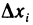 и суммируя по всем i от 1 до n, получаем
и суммируя по всем i от 1 до n, получаем 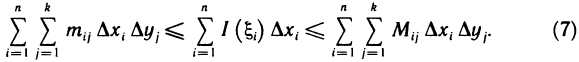
Пусть наибольший диаметр частичных прямоугольников 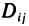 стремится к нулю
стремится к нулю  . Тогда и наибольшая из длин
. Тогда и наибольшая из длин 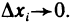 Крайние члены в (7), представляющие собой нижнюю и верхнюю суммы Дарбу, стремятся при этом к двойному интегралу (1) (см. сноску на с. 308). Таким образом, существует предел и среднего члена (7), равный тому же самому двойному интегралу. Но этот предел по определению определенного интеграла равен
Крайние члены в (7), представляющие собой нижнюю и верхнюю суммы Дарбу, стремятся при этом к двойному интегралу (1) (см. сноску на с. 308). Таким образом, существует предел и среднего члена (7), равный тому же самому двойному интегралу. Но этот предел по определению определенного интеграла равен 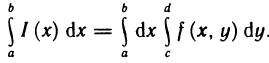
Тем самым доказано существование повторного интеграла и равенство (3). ■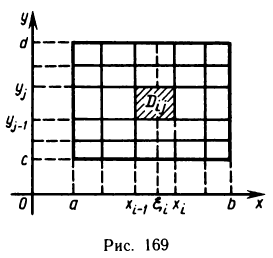
Замечание:
Если в теореме 13.3 поменять х и у ролями, то будет доказано существование повторного интеграла 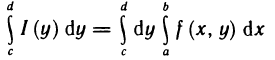
и справедливость равенства 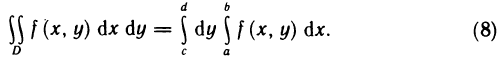
С помощью формул (3) и (8) двойной интеграл приводится к повторному. Например, в формуле (8) интегрирование сначала производится по х при постоянном у, а затем полученный результат интегрируется по у, т. е. последовательно вычисляются два определенных интеграла.
Пример:
Вычислить 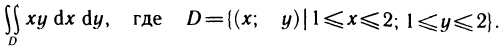
Решение:
Имеем 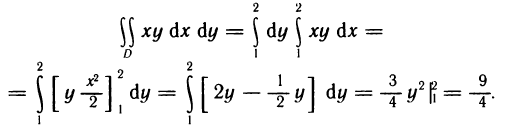
Случай криволинейной области
Теорема:
Пусть функция z=f(x, у) определена в области 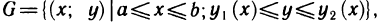 где
где 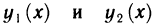 — непрерывные функции,
— непрерывные функции, 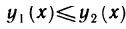 для
для 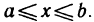 .Пусть также существует двойной интеграл
.Пусть также существует двойной интеграл 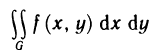
и для каждого х из отрезка [а, b] существует определенный интеграл 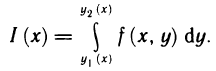
Тогда существует повторный интеграл 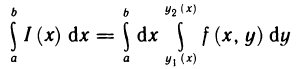
и справедливо равенство 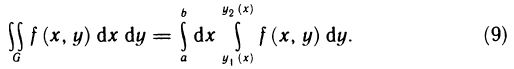 Доказательство:
Доказательство:
Положим 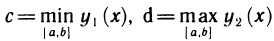 и заключим область G в прямоугольник
и заключим область G в прямоугольник 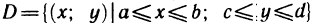 (рис. 170). Рассмотрим в этом прямоугольнике вспомогательную функцию
(рис. 170). Рассмотрим в этом прямоугольнике вспомогательную функцию 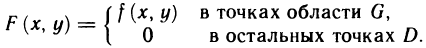
Эта функция удовлетворяет условиям предыдущей теоремы. Действительно, она интегрируема в области G, так как совпадает в ней с f (x, у), и интегрируема в остальной части D — G прямоугольника D, где она равна нулю. Следовательно, согласно свойству 3°
§ 1, она интегрируема и по всему прямоугольнику D. При этом 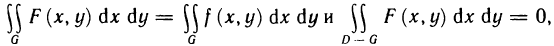
откуда 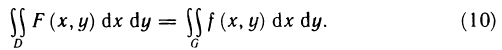
Далее, для каждого х из [а, b] существует интеграл  так как существует каждый из трех интегралов, стоящих справа. Действительно, отрезки
так как существует каждый из трех интегралов, стоящих справа. Действительно, отрезки  лежат вне области G и на них F (x, у) равна нулю, отсюда первый и третий интегралы
лежат вне области G и на них F (x, у) равна нулю, отсюда первый и третий интегралы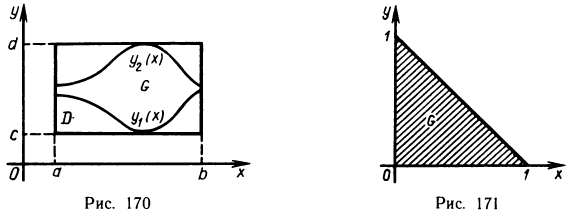
равны нулю, а второй интеграл существует по условию, так как 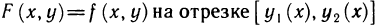 . Поэтому
. Поэтому 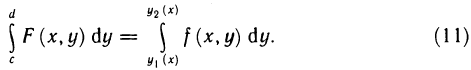
Таким образом, для функции F (х, у) выполнены все условия теоремы 13.3 и, следовательно, двойной интеграл от этой функции по прямоугольнику D может быть сведен к повторному 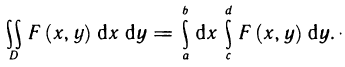
Отсюда и из равенств (10) и (11) получаем 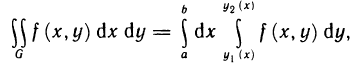
т. е. формулу (9). ■
Замечание:
Если в теореме 13.4 поменять ролями х и у, то теорема будет утверждать существование повторного интеграла 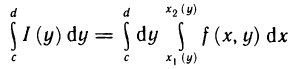
и равенства 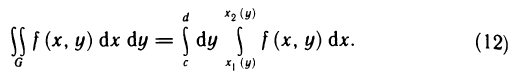
Пример:
Вычислить интеграл  по области
по области 
Решение:
Область G представляет собой треугольник, ограниченный осями координат и прямой 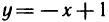 (рис. 171). Следовательно,
(рис. 171). Следовательно, 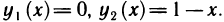 По формуле (9) имеем
По формуле (9) имеем 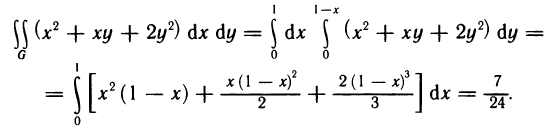
Данный интеграл можно вычислить и по формуле (12), если в G поменять х и у ролями. Тогда треугольник определяется неравенствами 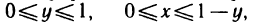 откуда
откуда 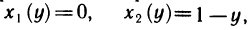 и легко проверить, что интеграл
и легко проверить, что интеграл 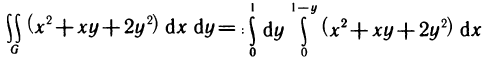 имеет то же самое значение.
имеет то же самое значение.
Замечание:
Если область G не удовлетворяет условиям теоремы 13.4 (например, прямые (вертикальные или горизонтальные) пересекают ее границу более чем в двух точках), то необходимо область G разбить на части, каждая из которых удовлетворяла бы условиям теоремы 13.4, и сводить к повторному каждый из соответствующих двойных интегралов отдельно.
Замена переменных в двойном интеграле
Пусть функция f (х, у) непрерывна в некоторой замкнутой ограниченной области G. Тогда для функции f (х, у) существует двойной интеграл 
Предположим, далее, что с помощью формул 
мы переходим к новым переменным 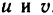 . Будем считать, что
. Будем считать, что 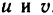 определяются из (2) единственным образом:
определяются из (2) единственным образом: 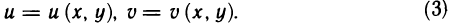
С помощью формул (3) каждой точке М (х; у) из области G ставится в соответствие некоторая точка 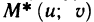 на координатной плоскости с прямоугольными координатами
на координатной плоскости с прямоугольными координатами 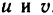 . Пусть множество всех точек
. Пусть множество всех точек 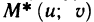 образует ограниченную замкнутую область G*. Формулы (2) называют формулами преобразования координат, а формулы (3) — формулами обратного преобразования.
образует ограниченную замкнутую область G*. Формулы (2) называют формулами преобразования координат, а формулы (3) — формулами обратного преобразования.
При сделанных предположениях можно доказать, что если функции (2) имеют в области G* непрерывные частные производные первого порядка и если определитель 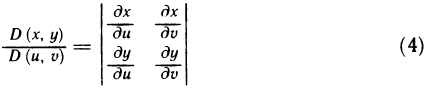
отличен в G от нуля, то для интеграла (1) справедлива формула замены переменных 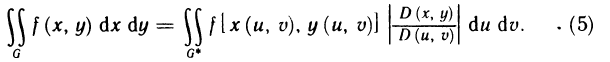
Определитель (4) называется функциональным определителем или якобианом (по имени немецкого математика Якоби) функций 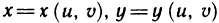 по переменным
по переменным 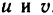 .
.
Коротко изложенное можно сформулировать в виде следующей теоремы.
Теорема:
Если преобразование (2) переводит замкнутую ограниченную область G в замкнутую ограниченную область G* и является взаимно однозначным и если функции (2) имеют в области G* непрерывные частные производные первого порядка и отличный от нуля якобиан (4), а функция f (х, у) непрерывна в области G, то справедлива формула замены переменных (5).
Доказательство теоремы достаточно сложное и здесь не приводится.
Как в двойном, так и в определенном интеграле замена переменных — важнейший способ приведения интеграла к виду, более удобному для вычисления.
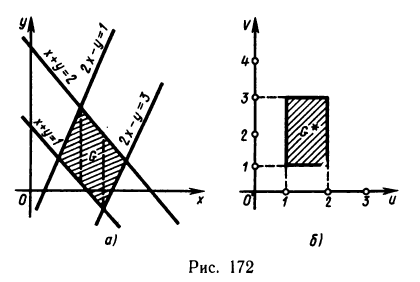
Пример:
Вычислить интеграл 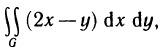 где G — параллелограмм, ограниченный прямыми
где G — параллелограмм, ограниченный прямыми 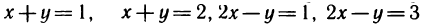 (рис. 172, а).
(рис. 172, а).
Решение:
Непосредственное вычисление этого интеграла достаточно громоздкое, так как для сведения его к повторному (сначала по у, а затем по х) необходимо область G разбить на три области (штриховые линии на рис. 172) и затем вычислить соответственно три интеграла. Однако простая замена переменных 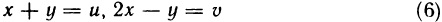
позволяет значительно упростить решение. Прямые 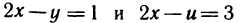 в системе координат Оху переходят в прямые
в системе координат Оху переходят в прямые 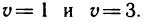 Осталось вычислить якобиан. Для этого выразим х и у через
Осталось вычислить якобиан. Для этого выразим х и у через  из равенств (6):
из равенств (6): 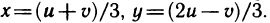
Следовательно, 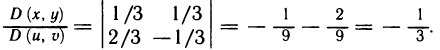
По формуле (5) окончательно получаем 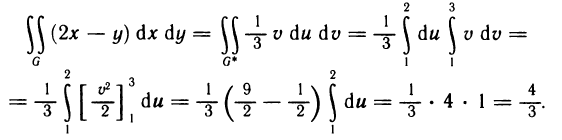
Замечание:
Если подынтегральная функция или уравнение границы области интегрирования содержат сумму 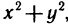 , то во многих случаях упрощение интеграла достигается преобразованием его к полярным координатам, так как данная сумма в полярных координатах
, то во многих случаях упрощение интеграла достигается преобразованием его к полярным координатам, так как данная сумма в полярных координатах 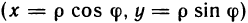 принимает достаточно простой вид
принимает достаточно простой вид 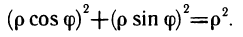
Пример:
Вычислить интеграл 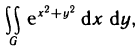 где G — четверть круга
где G — четверть круга 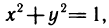 расположенная в I квадранте (рис. 173).
расположенная в I квадранте (рис. 173).
Решение:
Преобразуем интеграл к полярным координатам по формулам  Тогда
Тогда 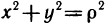 :
: 
Наглядно видно, что в области G р изменяется в пределах от 0 до 1, а  — от 0 до
— от 0 до  /2. Иначе говоря, область G преобразуется в прямоугольник
/2. Иначе говоря, область G преобразуется в прямоугольник 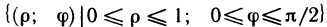 (рис. 173).
(рис. 173).
Таким образом, по формуле (5) получаем 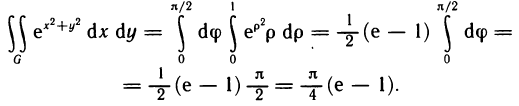
На практике при замене переменных нет необходимости детально строить область G*. Обычно выясняют пределы изменения новых координат, используя вид области G на плоскости Оху, что и сделано вначале в данном примере.
Некоторые геометрические и физические приложения двойных интегралов
Вычисление объема
Как известно, объем v криволинейного цилиндра, ограниченного сверху поверхностью z=f(x, у)>0, снизу плоскостью z=0 и с боковых сторон цилиндрической поверхностью, у которой образующие параллельны оси Oz, а направляющей служит контур области G, вычисляется по формуле 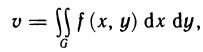
т. е. с помощью двойных интегралов можно вычислять объемы тел.
Пример:
Вычислить объем тела, ограниченного поверхностями  (рис. 174).
(рис. 174).
Решение:
Имеем 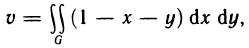
где G — треугольная область интегрирования, ограниченная прямыми 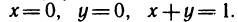 Расставляя пределы интегрирования в двойном интеграле, получаем
Расставляя пределы интегрирования в двойном интеграле, получаем 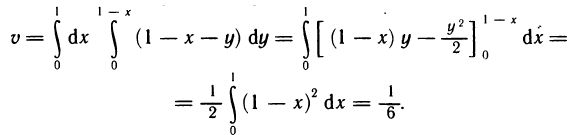
Вычисление площади
Как было установлено, площадь s области G может быть вычислена с помощью двойного интеграла по формуле 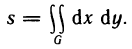
Эта формула более универсальна, чем соответствующая формула выражающая площадь криволинейной трапеции с помощью определенного интеграла, так как данная формула применима не только к криволинейным трапециям, но и к фигурам, расположенным произвольно по отношению к координатным осям.
Пример:
Вычислить площадь области G, ограниченной линиями 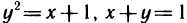 (рис. 175).
(рис. 175).
Решение:
Область G представляет собой фигуру, ограниченную слева параболой 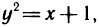 справа прямой
справа прямой 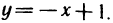 Решая совместно уравнения параболы и прямой, находим точки их пересечения:
Решая совместно уравнения параболы и прямой, находим точки их пересечения: 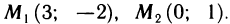 Следовательно, искомая площадь
Следовательно, искомая площадь 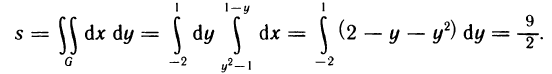
При вычислении двойных интегралов с помощью повторного интегрирования одним из главных моментов является расстановка пределов интегрирования. Если в данном примере выбрать другой порядок повторного интегрирования (сначала по у, а затем по х),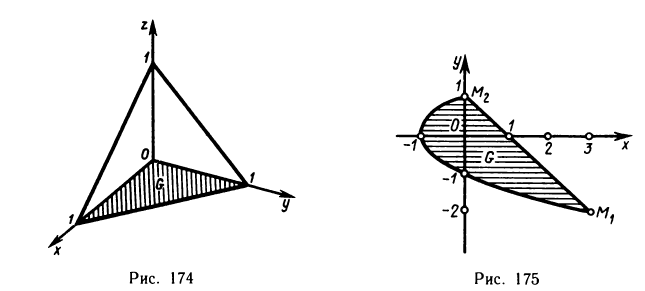
то область G предварительно пришлось бы разбить на две части (осью Оу), так как она ограничена сверху линией, заданной на отрезках 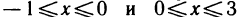 двумя различными уравнениями. Разумеется, был бы получен тот же результат, однако вычисления оказались бы более громоздкими.
двумя различными уравнениями. Разумеется, был бы получен тот же результат, однако вычисления оказались бы более громоздкими.
Поэтому полезно запомнить следующее правило: если все прямые, параллельные оси Оу, входят в область интегрирования G на линии, заданной одним уравнением, и выходят из области на линии, заданной одним уравнением, то внутренний интеграл целесообразно брать по переменной у, а внешний — по х аналогично, если все прямые, параллельные оси Ох, входят в область интегрирования на линии, заданной одним уравнением (в данном случае на параболе), и выходят на линии, заданной одним уравнением (в данном случае на прямой), то внутренний интеграл следует брать по переменной х, а внешний — по у: в этом случае область интегрирования не нужно разбивать на части.
Вычисление площади поверхности
С помощью двойных интегралов можно вычислять площади не только плоских фигур, но и кривых поверхностей.
Пусть поверхность S задана уравнением z=f (x, у), проекцией S на плоскость Оху является область G (рис. 176) и в этой области функция f (x, у) непрерывна и имеет непрерывные частные производные 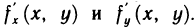
Для определения площади поверхности S разобьем область G произвольно на n частей G, без общих внутренних точек с площадями 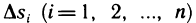 и обозначим через
и обозначим через 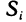 часть поверхности S, проекцией которой на плоскость Оху является частичная область
часть поверхности S, проекцией которой на плоскость Оху является частичная область 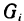 . Таким образом, поверхность S будет разбита на n частей.
. Таким образом, поверхность S будет разбита на n частей.
В каждой части 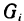 выберем произвольную точку
выберем произвольную точку  , на поверхности S ей будет соответствовать точка
, на поверхности S ей будет соответствовать точка 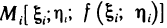 . Проведем через точку М, касательную плоскость к поверхности:
. Проведем через точку М, касательную плоскость к поверхности: 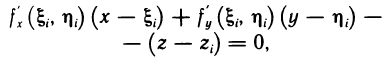
здесь х, у, z — координаты произвольной точки на плоскости; 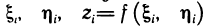 — координаты точки касания (см. гл. 12, § 4, п. 2). Напомним, что вектор
— координаты точки касания (см. гл. 12, § 4, п. 2). Напомним, что вектор 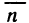 (нормаль), перпендикулярный касательной плоскости, имеет следующие координаты:
(нормаль), перпендикулярный касательной плоскости, имеет следующие координаты: 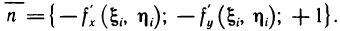 (Здесь вектор
(Здесь вектор 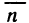 направлен противоположно вектору
направлен противоположно вектору 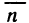 из гл. 12, § 4, п. 2. Данный вектор
из гл. 12, § 4, п. 2. Данный вектор 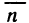 образует острый угол с осью Оz.)
образует острый угол с осью Оz.)
Рассмотрим на касательной плоскости ту ее часть, проекцией которой на плоскость Оху является область 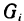 . Обозначим эту часть через
. Обозначим эту часть через 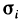 , а ее площадь через
, а ее площадь через 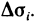 Площадь
Площадь 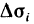 можно считать приближенно равной площади части S, поверхности, а сумму всех таких площадей
можно считать приближенно равной площади части S, поверхности, а сумму всех таких площадей 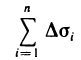
приближенным значением площади всей поверхности S.
За точное значение площади поверхности S примем по определению предел такой суммы 
где 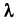 — наибольший из диаметров частичных областей
— наибольший из диаметров частичных областей 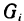 . Докажем, что этот предел существует и равен двойному интегралу
. Докажем, что этот предел существует и равен двойному интегралу 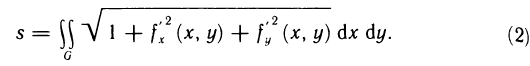
Обозначим через 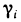 угол между вектором
угол между вектором 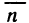 и осью Oz. Он равен углу между касательной плоскостью в точке
и осью Oz. Он равен углу между касательной плоскостью в точке 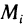 и плоскостью Оху. Так как область
и плоскостью Оху. Так как область 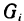 есть проекция
есть проекция 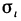 на плоскость Оху, то площади этих областей связаны соотношением
на плоскость Оху, то площади этих областей связаны соотношением 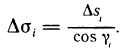
Действительно, данная формула, как известно, справедлива для треугольников. Она, очевидно, справедлива и для плоских многоугольников, так как плоский многоугольник можно разбить на несколько треугольников. Она также справедлива и для любой плоской фигуры площади 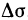 , ограниченной некоторой кривой, поскольку ее площадь можно рассматривать как предел площадей вписанных в нее многоугольников.
, ограниченной некоторой кривой, поскольку ее площадь можно рассматривать как предел площадей вписанных в нее многоугольников.
С другой стороны, как известно из аналитической геометрии, 
Следовательно,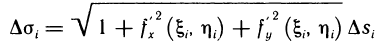
Подставляя значение 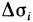 в сумму (1), получаем
в сумму (1), получаем 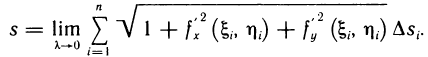
Стоящая под знаком предела сумма представляет собой интегральную сумму для функции 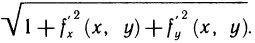
Так как эта функция по условию непрерывна в области G, то предел этой суммы при  существует и равен двойному интегралу (2), что и требовалось доказать.
существует и равен двойному интегралу (2), что и требовалось доказать.
Соотношение (2) представляет собой формулу, с помощью которой вычисляется площадь поверхностей, заданных уравнением z=f(x, у).
Пример:
Вычислить площадь той части плоскости 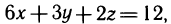 , которая заключена в первом октанте (рис. 177).
, которая заключена в первом октанте (рис. 177).
Решение:
Так как функция 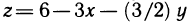 и область G, являющаяся проекцией данной части поверхности на плоскость Оху, удовлетворяют сформулированным выше условиям, то искомую площадь можно вычислить по формуле (2). Имеем
и область G, являющаяся проекцией данной части поверхности на плоскость Оху, удовлетворяют сформулированным выше условиям, то искомую площадь можно вычислить по формуле (2). Имеем 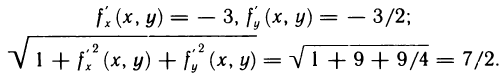
Областью G является треугольник, ограниченный осями Ох, Оу и прямой 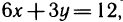 получаемой из уравнения данной плоскости при z=0. Расставляя пределы интегрирования в двойном интеграле, получаем
получаемой из уравнения данной плоскости при z=0. Расставляя пределы интегрирования в двойном интеграле, получаем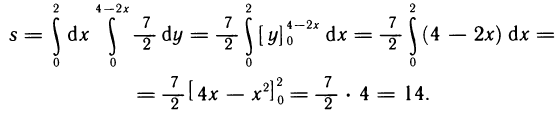
Вычисление массы пластинки
Рассмотрим на плоскости Оху материальную пластинку, т. е. некоторую область G, по которой распределена масса m с плотностью р (х, у). Вычислим по заданной плотности р (х, у) массу т этой пластинки, считая, что р (х, у)— непрерывная функция. Разобьем G произвольно на n частей  и обозначим через
и обозначим через  массы этих частей.
массы этих частей. 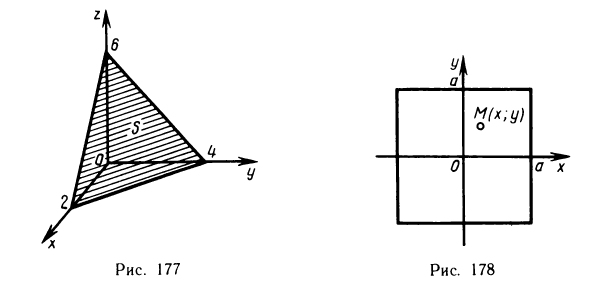
В каждой части произвольно возьмем точку  . Массу
. Массу  каждой такой части
каждой такой части 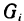 можно считать приближенно равной
можно считать приближенно равной 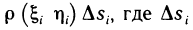 — площадь
— площадь 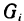 , а масса m всей пластинки приближенно равна сумме
, а масса m всей пластинки приближенно равна сумме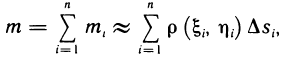
которая является интегральной суммой для непрерывной функции
р (х, у) в области G. В пределе при 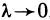 , очевидно, получим точное значение массы пластинки, равное двойному интегралу от функции р (х, у) по области G, т. е.
, очевидно, получим точное значение массы пластинки, равное двойному интегралу от функции р (х, у) по области G, т. е. 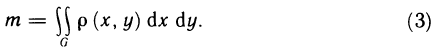
Пример:
Определить массу квадратной пластинки со стороной 2а, если плотность р (x, у) в каждой точке М (х; у) пропорциональна квадрату расстояния от точки М до точки пересечения диагоналей, и коэффициент пропорциональности равен k.
Решение:
Выберем систему координат так, как показано на рис. 178. После этого можно найти функцию р (х, у) исходя из условия задачи. Пусть М (х; у) — произвольная точка квадратной пластинки. Тогда квадрат расстояния от точки М до точки пересечения диагоналей равен 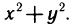 Следовательно, плотность в точке М
Следовательно, плотность в точке М 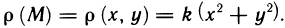
По формуле (3) имеем 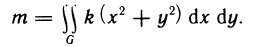
Учитывая, что подынтегральная функция четна относительно х и у, а область интегрирования симметрична относительно осей координат, можно ограничиться вычислением интеграла по той части области G, которая расположена в I четверти, т. е. 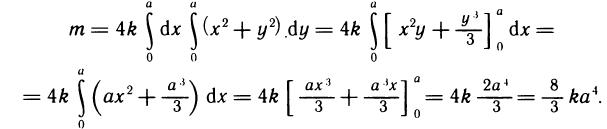
Вычисление координат центра масс пластинки
Найдем координаты центра масс пластинки, занимающей в плоскости Оху некоторую область G. Пусть р (х; у) — плотность этой пластинки в точке М (х; у), причем р (х; у)—непрерывная функция. Разбив область G на части  , выберем в каждой из этих частей некоторую точку
, выберем в каждой из этих частей некоторую точку  и будем приближенно считать массу
и будем приближенно считать массу 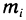 каждой из частей пластинки равной
каждой из частей пластинки равной 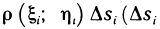 — площадь
— площадь 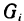 ).
).
Если считать, что каждая из этих масс сосредоточена в одной точке, а именно в точке 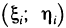 , то для координат
, то для координат 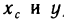 , центра масс такой системы материальных точек получим следующие выражения:
, центра масс такой системы материальных точек получим следующие выражения: 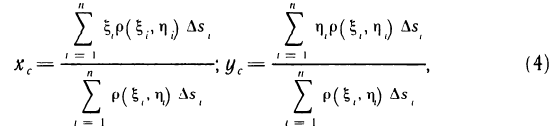
которые представляют собой приближенные значения координат центра масс пластинки. Чтобы получить точные значения этих координат, необходимо в (4) перейти к пределу при  . При этом интегральные суммы перейдут в соответствующие интегралы и мы получим, что координаты центра масс пластинки определяются формулами
. При этом интегральные суммы перейдут в соответствующие интегралы и мы получим, что координаты центра масс пластинки определяются формулами 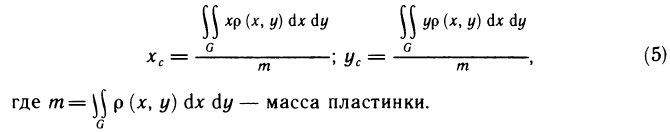
Если пластинка однородна, т. е. 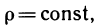 то формулы координат центра масс упрощаются:
то формулы координат центра масс упрощаются: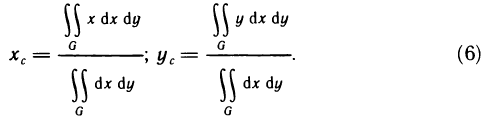
Величины 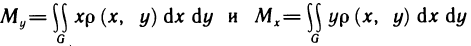 в формулах (5) называются статическими моментами пластинки относительно осей Оу и Ох.
в формулах (5) называются статическими моментами пластинки относительно осей Оу и Ох.
Таким образом, вычисление координат центра масс пластинки сводится к вычислению трех двойных интегралов.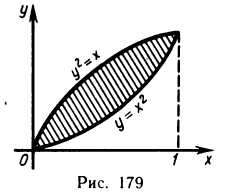
Пример:
Найти координаты центра масс однородной пластинки, ограниченной двумя параболами 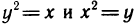 (рис. 179).
(рис. 179).
Решение:
Координаты центра масс данной пластинки найдем по формулам (6). Сначала вычислим массу пластинки 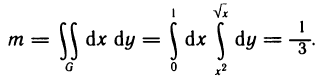
Далее вычислим статические моменты ее относительно осей координат: 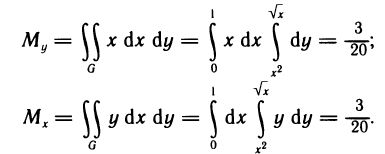
Затем по формулам (6) найдем 
Итак, 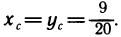
Вычисление момента инерции пластинки
Как известно, момент инерции материальной точки относительно некоторой оси равен произведению массы точки на квадрат ее расстояния до этой оси, а момент инерции системы материальных точек равен сумме моментов инерции этих точек.
Пусть область G плоскости Оху занята пластинкой, имеющей непрерывную плотность р (х, у). Разбив область G на части 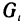 площади которых равны
площади которых равны 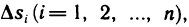 и выбрав в каждой из них некоторую точку
и выбрав в каждой из них некоторую точку 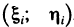 , заменим пластинку системой материальных точек с массами
, заменим пластинку системой материальных точек с массами 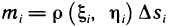 и координатами
и координатами 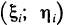 . Момент инерции такой системы точечных масс, например, относительно оси Оу равен
. Момент инерции такой системы точечных масс, например, относительно оси Оу равен 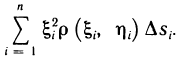
Примем это выражение за приближенное значение момента инерции пластинки. Но оно же представляет собой интегральную сумму для непрерывной функции 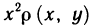 . Переходя к пределу при
. Переходя к пределу при 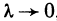 , получаем для момента инерции пластинки относительно оси Оу следующую формулу:
, получаем для момента инерции пластинки относительно оси Оу следующую формулу: 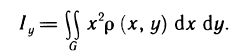
Аналогично, момент инерции пластинки относительно оси Ох равен 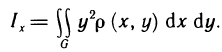
Найдем момент инерции 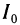 пластинки относительно начала координат. Принимая во внимание, что момент инерции материальной точки с массой m относительно начала координат равен
пластинки относительно начала координат. Принимая во внимание, что момент инерции материальной точки с массой m относительно начала координат равен 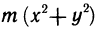 , рассуждая, как и выше, получаем, что
, рассуждая, как и выше, получаем, что 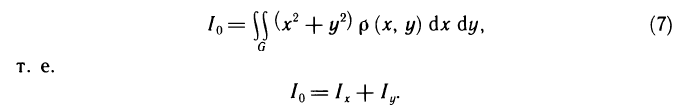
Пример:
Найти момент инерции круга радиуса R с постоянной плотностью р (x, у)=1 относительно начала координат.
Решение:
По формуле (7) имеем 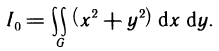
Перейдем к полярным координатам. Уравнение окружности (границы круга) в полярных координатах имеет вид 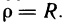 Поэтому
Поэтому 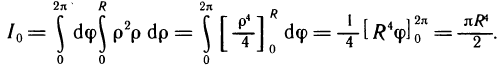
Криволинейные интегралы
Обобщим понятие определенного интеграла на случай, когда областью интегрирования является отрезок некоторой кривой, лежащей в плоскости.
Интегралы такого рода называются криволинейными. Они имеют широкое применение в различных разделах математики.
Различают два типа криволинейных интегралов: криволинейные интегралы первого и второго рода.
Определение криволинейного интеграла первого рода
Рассмотрим на плоскости Оху некоторую кривую АВ, гладкую или кусочно-гладкую, и предположим, что функция z=f(x, у) определена и ограничена на кривой АВ.
Разобьем кривую АВ произвольно на п частей точками  выберем на каждой из частичных дуг
выберем на каждой из частичных дуг 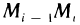 произвольную точку
произвольную точку 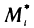 (рис. 180) и составим сумму
(рис. 180) и составим сумму 
где 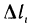 — длина дуги
— длина дуги  Сумма (1) называется интегральной суммой для функции
Сумма (1) называется интегральной суммой для функции 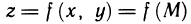 по кривой АВ. Обозначим через
по кривой АВ. Обозначим через 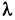 наибольшую из длин частичных дуг
наибольшую из длин частичных дуг 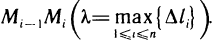
Определение:
Если интегральная сумма (1) при  имеет предел, равный I, то этот предел называется криволинейным интегралом первого рода от функции f (х, у) по кривой А В и обозначается одним из следующих символов
имеет предел, равный I, то этот предел называется криволинейным интегралом первого рода от функции f (х, у) по кривой А В и обозначается одним из следующих символов 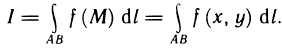
В этом случае функция f (x, у) называется интегрируемой вдоль кривой АВ, сама кривая АВ — контуром интегрирования, А — начальной, а В — конечной точками интегрирования.
Криволинейный интеграл первого рода легко сводится к определенному интегралу. Действительно, приняв на кривой АВ за параметр длину дуги 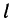 , отсчитываемую от точки А, получим параметрическое представление кривой
, отсчитываемую от точки А, получим параметрическое представление кривой 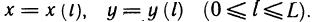 При этом функция f (х, у), заданная вдоль АВ, становится сложной функцией параметра
При этом функция f (х, у), заданная вдоль АВ, становится сложной функцией параметра 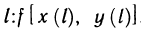 . Обозначив через
. Обозначив через 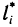 значение параметра
значение параметра 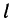 , отвечающее точке
, отвечающее точке 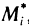 , а через
, а через 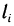 — отвечающее точке
— отвечающее точке 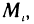 перепишем интегральную сумму (1) в виде
перепишем интегральную сумму (1) в виде 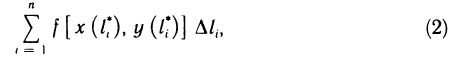
где 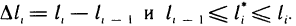 Сумма (2) является интегральной для определенного интеграла от функции
Сумма (2) является интегральной для определенного интеграла от функции 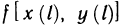 на отрезке [0, L]. Поскольку интегральные суммы (1) и (2) равны между собой, равны и соответствующие им интегралы, т. е.
на отрезке [0, L]. Поскольку интегральные суммы (1) и (2) равны между собой, равны и соответствующие им интегралы, т. е. 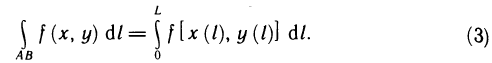
Заметим, что формула (3) не только выражает криволинейный интеграл через определенный, но и доказывает существование криволинейного интеграла от функции f (х, у), непрерывной вдоль рассматриваемой кривой АВ.
Как было показано, криволинейный интеграл первого рода непосредственно сводится к определенному, однако между этими понятиями имеется следующее различие. В интегральной сумме (1) величины 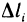 обязательно положительны, независимо от того, какую точку кривой АВ считать начальной, а какую — конечной, т. е.
обязательно положительны, независимо от того, какую точку кривой АВ считать начальной, а какую — конечной, т. е. 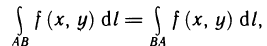
в то время как определенный интеграл 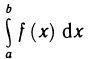 при перестановке пределов интегрирования меняет знак. В остальном криволинейный интеграл первого рода обладает теми же свойствами, что и определенный интеграл. Это непосредственно вытекает из формулы (3).
при перестановке пределов интегрирования меняет знак. В остальном криволинейный интеграл первого рода обладает теми же свойствами, что и определенный интеграл. Это непосредственно вытекает из формулы (3).
Криволинейный интеграл первого рода, так же как и определенный, имеет геометрический смысл. Если определенный интеграл 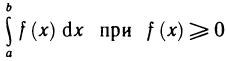 представляет собой площадь криволинейной трапеции, то криволинейный интеграл
представляет собой площадь криволинейной трапеции, то криволинейный интеграл 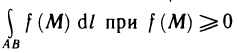 численно равен площади куска цилиндрической поверхности, которая составлена из перпендикуляров к плоскости Оху, восставленных в точках М (х; у) кривой АВ и имеющих переменную длину f (М) (рис. 181).
численно равен площади куска цилиндрической поверхности, которая составлена из перпендикуляров к плоскости Оху, восставленных в точках М (х; у) кривой АВ и имеющих переменную длину f (М) (рис. 181).
В частности, если АВ — не кривая, а отрезок прямой [а, b], расположенный на оси Ох, то 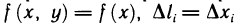 и криволинейный интеграл будет обычным определенным интегралом.
и криволинейный интеграл будет обычным определенным интегралом.
Наконец, если положить 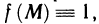 то получим криволинейный интеграл
то получим криволинейный интеграл 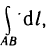 значение которого есть длина дуги кривой АВ.
значение которого есть длина дуги кривой АВ.
Таким образом, с помощью криволинейного интеграла первого рода можно вычислять площадь цилиндрических поверхностей и длины дуг. Кроме этого, криволинейный интеграл первого рода имеет широкое применение в физике. С его помощью можно, как это делали в случае двойных интегралов, находить массу материальной кривой по ее плотности, моменты инерции относительно координатных осей, координаты центра масс такой кривой и т. д.
Вычисление криволинейных интегралов первого рода
Вычисление криволинейных интегралов первого рода сводится к вычислению определенных интегралов.
Пусть кривая АВ задана параметрически уравнениями 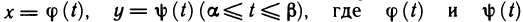 — непрерывные вместе со своими производными
— непрерывные вместе со своими производными 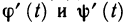 функции, a f(x, у) — функция, непрерывная вдоль этой кривой, причем для определенности будем считать, что точке А соответствует значение
функции, a f(x, у) — функция, непрерывная вдоль этой кривой, причем для определенности будем считать, что точке А соответствует значение 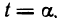 точке В — значение
точке В — значение 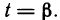 Тогда для любой точки
Тогда для любой точки 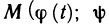 кривой АВ длину
кривой АВ длину 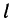 дуги AM можно рассматривать как функцию параметра
дуги AM можно рассматривать как функцию параметра 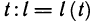 и вычислять ее (гл. 8, § 10, п. 3) по формуле
и вычислять ее (гл. 8, § 10, п. 3) по формуле 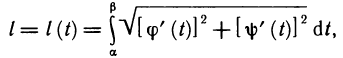
откуда, согласно правилу дифференцирования интеграла по верхнему пределу, 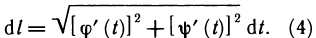
Заменяя переменную 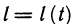 в определенном интеграле в правой части равенства (3) и учитывая (4), получаем
в определенном интеграле в правой части равенства (3) и учитывая (4), получаем 
Пример:
Вычислить криволинейный интеграл 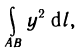
где АВ — часть окружности 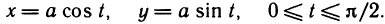
Решение:
Так как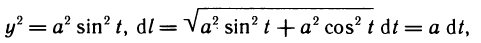
то по формуле (5) получаем 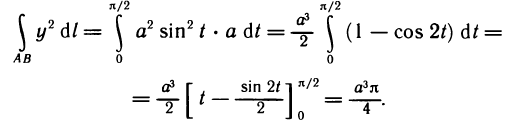
В частности, если кривая АВ задана уравнением у=у(х), 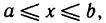 где у(х) — непрерывно дифференцируемая функция, то, принимая х за параметр (t=х), из формулы (5) имеем
где у(х) — непрерывно дифференцируемая функция, то, принимая х за параметр (t=х), из формулы (5) имеем 
Пример:
Вычислить криволинейный интеграл 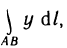
где АВ — дуга параболы 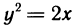 от точки (0; 0) до точки (2; 2). Решение:
от точки (0; 0) до точки (2; 2). Решение:
Имеем 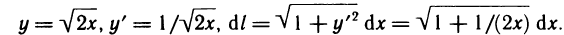 По формуле (6) получаем
По формуле (6) получаем 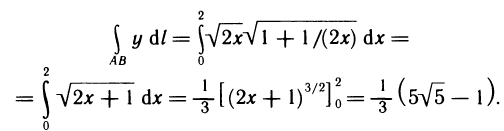
Замечание:
Формула (4) представляет самостоятельный интерес. Возводя в квадрат, получаем: 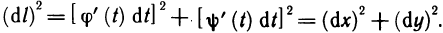 Это равенство дает простое геометрическое истолкование дифференциала дуги dl. Учитывая, что дифференциал функции у=у(х) равен приращению ординаты касательной (гл. 5, § 3, п. 1), получаем, что дифференциал дуги dl (см. рис. 185) равен длине отрезка касательной к кривой АВ от точки касания с абциссой х до точки
Это равенство дает простое геометрическое истолкование дифференциала дуги dl. Учитывая, что дифференциал функции у=у(х) равен приращению ординаты касательной (гл. 5, § 3, п. 1), получаем, что дифференциал дуги dl (см. рис. 185) равен длине отрезка касательной к кривой АВ от точки касания с абциссой х до точки 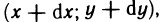 т. е. гипотенузе прямоугольного треугольника с катетами
т. е. гипотенузе прямоугольного треугольника с катетами 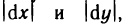 а равенство
а равенство 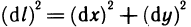 представляет собой теорему Пифагора.
представляет собой теорему Пифагора.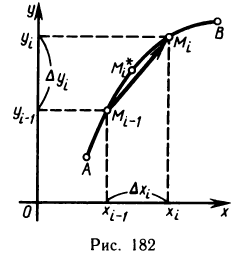
Определение криволинейного интеграла второго рода
Пусть на кривой АВ определены две ограниченные функции  . Разобьем кривую АВ на n частей точками
. Разобьем кривую АВ на n частей точками  Обозначим через
Обозначим через  , проекции вектора
, проекции вектора 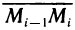 , на оси координат (рис. 182), на каждой частичной дуге
, на оси координат (рис. 182), на каждой частичной дуге 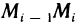 возьмем произвольную точку
возьмем произвольную точку 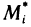 и составим интегральную сумму для функции
и составим интегральную сумму для функции 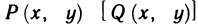 :
: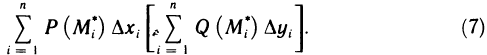
Определение:
Если интегральная сумма (7) при 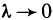
 — длина дуги
— длина дуги  ) имеет предел, равный I, то этот предел называется криволинейным интегралом второго рода от функции
) имеет предел, равный I, то этот предел называется криволинейным интегралом второго рода от функции 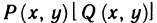 по кривой АВ и обозначается символом
по кривой АВ и обозначается символом 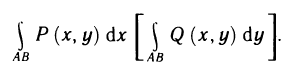
Сумму 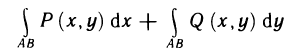
называют общим криволинейным интегралом второго рода и обозначают символом 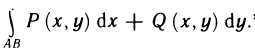
Криволинейные интегралы второго рода, как и интегралы первого рода, легко сводятся к определенным интегралам.
Действительно, пусть кривая АВ задана параметрически уравнениями 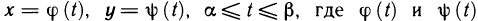 — непрерывные вместе со своими производными
— непрерывные вместе со своими производными 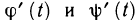 функции, причем точке А кривой соответствует значение
функции, причем точке А кривой соответствует значение 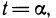 точке В — значение
точке В — значение 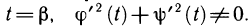 Пусть функции
Пусть функции
Р (х, у) и Q (х, у) непрерывны вдоль кривой АВ. Тогда справедливы следующие формулы: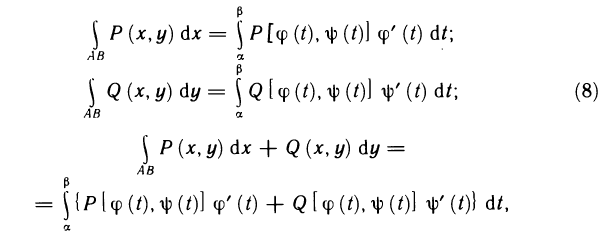 сводящие криволинейные интегралы к определенным интегралам.
сводящие криволинейные интегралы к определенным интегралам.
Докажем первую из формул (8): 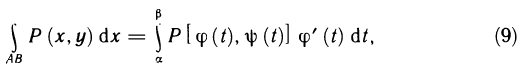
вторая формула доказывается аналогично, а третья получается в результате сложения первой и второй.
Пусть точкам 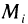 разбиения кривой АВ соответствуют значения
разбиения кривой АВ соответствуют значения 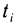 параметра t, точкам
параметра t, точкам 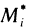 — значения
— значения 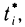 т. е.
т. е. 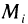 имеет координаты
имеет координаты 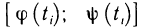 , а
, а 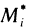 — координаты
— координаты 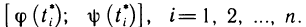 Функция Р (х, у) на кривой является сложной функцией параметра t:
Функция Р (х, у) на кривой является сложной функцией параметра t: 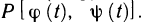 Так как функции
Так как функции 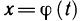 и
и 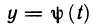 непрерывны на отрезке
непрерывны на отрезке 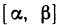 , а функция Р (х, у) непрерывна вдоль кривой АВ, то по теореме о непрерывности сложной функции функция
, а функция Р (х, у) непрерывна вдоль кривой АВ, то по теореме о непрерывности сложной функции функция 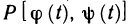 непрерывна на отрезке
непрерывна на отрезке 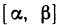 .
.
Составим интегральную сумму (7) для функции Р (х, у): 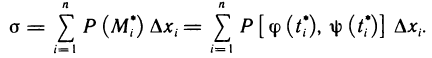
Так как 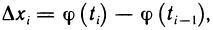 то по формуле Ньютона—Лейбница
то по формуле Ньютона—Лейбница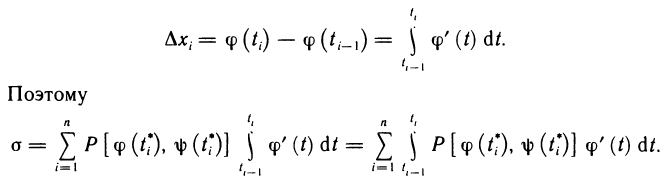
С другой стороны, так как функция 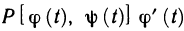 является непрерывной функцией на
является непрерывной функцией на 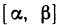 , то для нее существует определенный интеграл, стоящий в формуле (9) справа. Запишем его в виде суммы интегралов по частичным отрезкам
, то для нее существует определенный интеграл, стоящий в формуле (9) справа. Запишем его в виде суммы интегралов по частичным отрезкам 

Рассмотрим и оценим разность 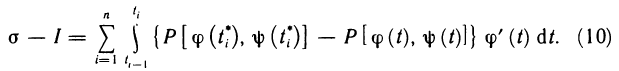
Из непрерывности функции 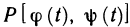 на
на 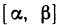 по теореме Кантора следует ее равномерная непрерывность на
по теореме Кантора следует ее равномерная непрерывность на 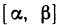 . А это означает, что для любого
. А это означает, что для любого 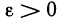 существует
существует 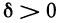 такое, что при
такое, что при  выполняется неравенство
выполняется неравенство 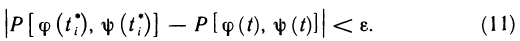
Из непрерывности функции 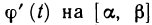 следует ее ограниченность на
следует ее ограниченность на 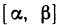 , т. е. существует число k такое, что
, т. е. существует число k такое, что 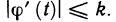
Используя (11) и (12), получаем для разности (10) следующую оценку: 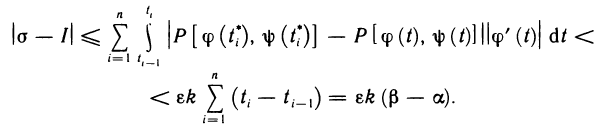
Отсюда, в силу произвольности  , следует, что
, следует, что 
Но при 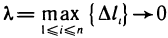 также
также 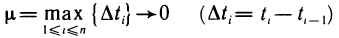 и наоборот. В самом деле,
и наоборот. В самом деле, 
Из непрерывности функций 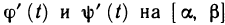 следует непрерывность функции
следует непрерывность функции 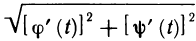 на
на 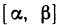 . Но тогда
. Но тогда 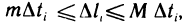 где m и М — минимальное и максимальное значения функции
где m и М — минимальное и максимальное значения функции 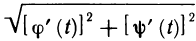 на отрезке
на отрезке 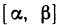 , причем m>0 и М>0 в силу условия
, причем m>0 и М>0 в силу условия 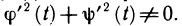 Из левого неравенства следует, что
Из левого неравенства следует, что  при
при  , а из правого, что
, а из правого, что  при
при  . Следовательно, из (13) имеем
. Следовательно, из (13) имеем 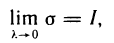
т. е. существует криволинейный интеграл 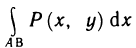 и справедлива формула (9).
и справедлива формула (9).
Криволинейный интеграл второго рода обладает свойствами, аналогичными свойствам определенного интеграла, что непосредственно вытекает из формул (8).
В отличие от криволинейного интеграла первого рода криволинейный интеграл второго рода зависит от того, в каком направлении (от А к В или от В к А) проходится кривая АВ, и меняет знак при изменении направления обхода кривой, т. е. 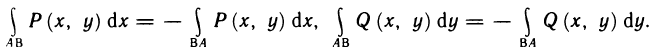
Действительно, изменив направление обхода кривой, мы соответственно изменим знаки проекций 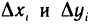 , в суммах (7), и, следовательно, сами суммы и их пределы изменят знак.
, в суммах (7), и, следовательно, сами суммы и их пределы изменят знак.
Таким образом, при вычислении криволинейных интегралов второго рода необходимо учитывать направление интегрирования.
В случае, когда L замкнутая кривая, т. е. когда точка В совпадает с точкой А, из двух возможных направлений обхода замкнутого контура L условимся называть положительным то направление, при котором область, лежащая внутри этого контура, остается слева по отношению к точке, совершающей обход. Противоположное направление обхода контура L условимся называть отрицательным.
Криволинейный интеграл по замкнутому контуру L, пробегаемому в положительном направлении, часто обозначают символом 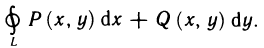
Вычисление криволинейных интегралов второго рода
Криволинейные интегралы второго рода вычисляют сведением их к определенным интегралам по формулам (8).
В частности, если кривая АВ задана уравнением вида  где у(х) — непрерывно дифференцируемая функция, то, принимая х за параметр (t=x), из формул (8) получаем
где у(х) — непрерывно дифференцируемая функция, то, принимая х за параметр (t=x), из формул (8) получаем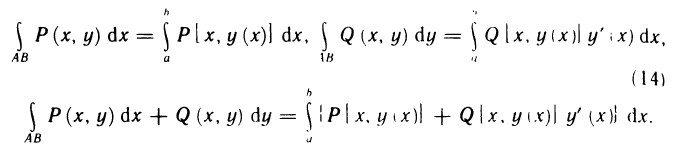
Аналогичные формулы имеют место, если кривая АВ задана уравнением вида х=х(у).
Пример:
Вычислить интеграл 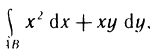 где АВ — четверть окружности
где АВ — четверть окружности 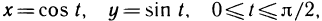 А соответствует t=0, В соответствует
А соответствует t=0, В соответствует 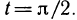
Решение:
Имеем  По третьей из формул (8) получаем
По третьей из формул (8) получаем 
Пример:
Вычислить интеграл 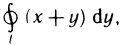 где L — контур прямоугольника, образованного прямыми х=0, y=0, х=1 и y=1 (рис. 183).
где L — контур прямоугольника, образованного прямыми х=0, y=0, х=1 и y=1 (рис. 183).
Решение:
На рис. 183 положительное направление обхода контура L обозначено стрелками. Разбивая весь контур интегрирования на части, запишем: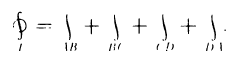
Легко заметить, что интегралы вдоль участков АВ и CD равны нулю, так как на них у является постоянным и, следовательно, dу=0. Поэтому остается вычислить интегралы по участкам ВС и DA. По формуле, аналогичной первой из формул (14) [заменяя 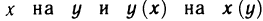 ], получаем
], получаем 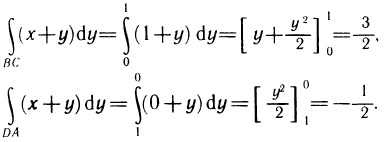
Таким образом, окончательно имеем 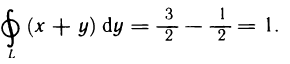
Пример:
Вычислить интеграл  где:
где:  Решение:
Решение:
По третьей формуле (14) имеем: 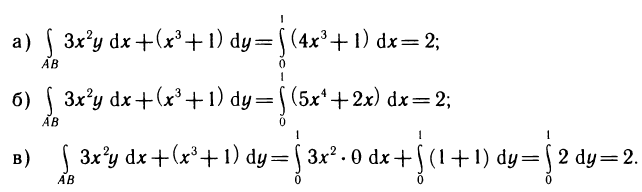
Заметим, что взяв три различных пути, соединяющих одни и те же точки, мы получили три одинаковых результата. Это обстоятельство не является случайным. Причина его будет раскрыта в § 7.
Связь между криволинейными интегралами первого и второго рода
Обозначим через 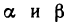 углы, составляемые с осями координат направленной касательной к кривой АВ в точке М (х; у) (рис. 185); тогда получим соотношения
углы, составляемые с осями координат направленной касательной к кривой АВ в точке М (х; у) (рис. 185); тогда получим соотношения 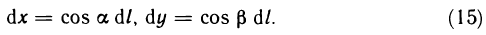
Заменяя в криволинейных интегралах второго рода dх и dу их выражениями (15), преобразуем эти интегралы в криволинейные интегралы первого рода: 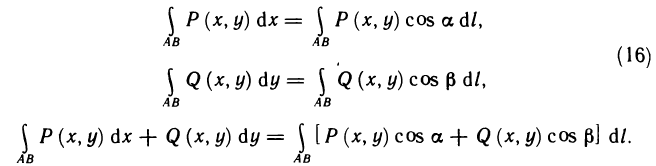
Таким образом, формулы (16) выражают криволинейные интегралы второго рода через криволинейные интегралы первого рода и устанавливают связь между ними. При изменении направления движения точки по кривой на противоположное  , dx и dy меняют знак, и формулы (16) остаются в силе.
, dx и dy меняют знак, и формулы (16) остаются в силе.
В заключение заметим, что были рассмотрены криволинейные интегралы для плоских кривых. Однако их определение и свойства нетрудно перенести и на пространственные кривые.
Пусть АВ — пространственная кривая и на этой кривой определены функции 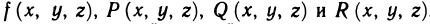 . Тогда по аналогии со случаем плоской кривой можно определить криволинейный интеграл первого рода
. Тогда по аналогии со случаем плоской кривой можно определить криволинейный интеграл первого рода 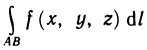 и криволинейные
и криволинейные 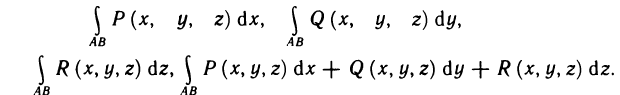
Техника вычисления таких интегралов не отличается по существу от техники вычисления интегралов по плоской кривой.
Формула Грина
Формула Грина устанавливает связь между криволинейными и двойными интегралами. Она имеет широкое применение как в самом анализе, так и в его приложениях.
Докажем эту формулу для замкнутой области, граница которой пересекается с прямыми, параллельными осям координат, не более чем в двух точках. Для краткости будем называть такие области простыми: Предполагается, что контур, ограничивающий область, гладкий или кусочно-гладкий.
Теорема:
Пусть G — некоторая простая замкнутая область, ограниченная контуром L, и пусть функции Р (х, у) и Q (х, у) непрерывны вместе со своими частными производными 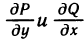 в данной области. Тогда имеет место формула
в данной области. Тогда имеет место формула 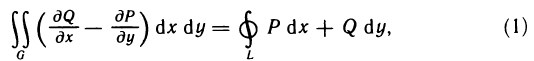
называемая формулой Грина.
Доказательство:
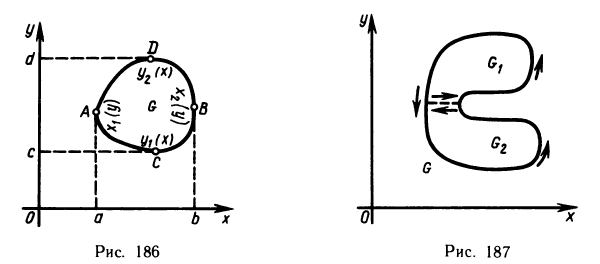
Пусть контур L, ограничивающий область G, может быть задан как уравнениями 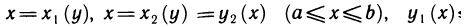 так и уравнениями
так и уравнениями 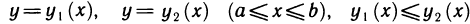 (рис. 186). Рассмотрим сначала область G, определенную неравенствами
(рис. 186). Рассмотрим сначала область G, определенную неравенствами 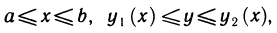 и преобразуем двойной интеграл
и преобразуем двойной интеграл 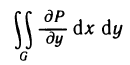
в криволинейный. Для этого сведем его к повторному интегралу и по формуле Ньютона—Лейбница выполним интегрирование по у. Получим 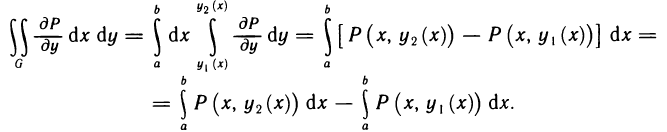
Каждый из этих двух определенных интегралов равен криволинейному интегралу второго рода, взятому по соответствующей кривой (см. формулы (14), § 5), а именно: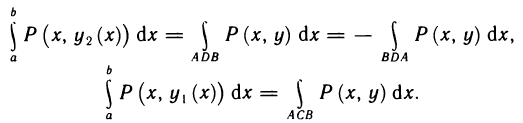
Таким образом, 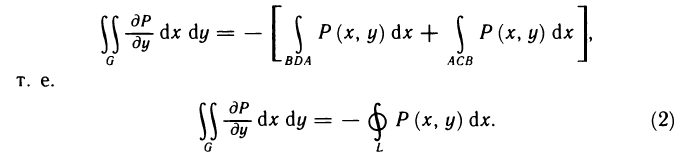 Аналогично доказывается формула
Аналогично доказывается формула 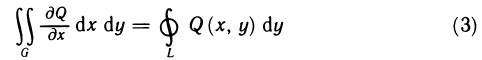
при этом область G задается неравенствами 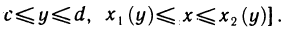
Вычитая из равенства (3) почленно равенство (2), получаем искомую формулу (1).
Замечание. Формула Грина остается справедливой для всякой замкнутой области G, которую можно разбить проведением дополнительных линий на конечное число простых замкнутых областей. Действительно, пусть область G с границей L имеет вид, изображенный на рис. 187. Разобьем ее на две простые области 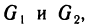 для каждой из которых справедлива формула (1). Напишем отдельно формулу Грина для
для каждой из которых справедлива формула (1). Напишем отдельно формулу Грина для 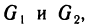 и сложим почленно полученные равенства. Слева будем иметь двойной интеграл по всей области G, а справа — криволинейный интеграл по контуру L области С, так как криволинейный интеграл по вспомогательной кривой берется дважды в противоположных направлениях и при суммировании взаимно уничтожается.
и сложим почленно полученные равенства. Слева будем иметь двойной интеграл по всей области G, а справа — криволинейный интеграл по контуру L области С, так как криволинейный интеграл по вспомогательной кривой берется дважды в противоположных направлениях и при суммировании взаимно уничтожается.
Пример:
С помощью формулы Грина вычислить криволинейный интеграл 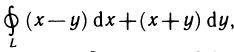 где L — окружность
где L — окружность 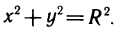
Решение:
Функции 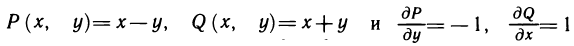 непрерывны в замкнутом круге
непрерывны в замкнутом круге 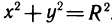 .
.
Следовательно, по теореме 13.6 формула Грина применима к данному интегралу. Имеем 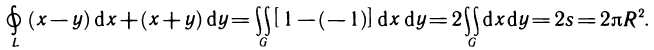 Заметим, что полученный результат легко проверить непосредственно вычислением данного интеграла.
Заметим, что полученный результат легко проверить непосредственно вычислением данного интеграла.
Условия независимости криволинейного интеграла от пути интегрирования
Как уже отмечалось при решении примера 5 (см. § 5, п. 4), в некоторых случаях величина криволинейного интеграла 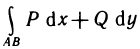 не зависит от пути интегрирования, а зависит только от начальной и конечной точек А и В пути интегрирования. Выясним, при каких условиях такая независимость имеет место. В исследовании этого вопроса важную роль играет формула Грина. Уточним, какие области будут рассматриваться далее.
не зависит от пути интегрирования, а зависит только от начальной и конечной точек А и В пути интегрирования. Выясним, при каких условиях такая независимость имеет место. В исследовании этого вопроса важную роль играет формула Грина. Уточним, какие области будут рассматриваться далее.
Определение:
Плоская область G называется односвязной, если каков бы ни был замкнутый контур L, лежащий внутри этой области, ограниченная этим контуром часть плоскости целиком принадлежит области G.
Образно говоря, односвязность области означает, что область не имеет «дыр». Например, односвязными областями являются внутренность круга, эллипса, многоугольника и т. п. Простейшим примером неодносвязной области служит область, заключенная между окружностями 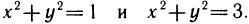 В самом деле, окружность
В самом деле, окружность 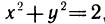 , лежащая в этой области, содержит внутри себя точки, которые не принадлежат данной области, например начало координат (0; 0).
, лежащая в этой области, содержит внутри себя точки, которые не принадлежат данной области, например начало координат (0; 0).
Теорема:
Пусть функции Р (х, у) и Q (х, у) определены и непрерывны вместе со своими частными производными 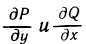 в некоторой замкнутой односвязной области G. Тогда следующие четыре условия эквивалентны, т. е. выполнение любого из них влечет за собой выполнение остальных трех:
в некоторой замкнутой односвязной области G. Тогда следующие четыре условия эквивалентны, т. е. выполнение любого из них влечет за собой выполнение остальных трех:
1) для любой замкнутой кусочно-гладкой кривой L, расположенной в G, 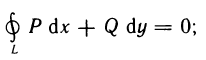
2) для любых двух точек А и В области G значение интеграла 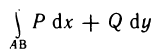
не зависит от выбора пути интегрирования, целиком лежащего в G;
3) выражение 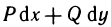 представляет собой полный дифференциал некоторой функции, определенной в области G. Иными словами, существует такая функция F (х, у), определенная в G, что
представляет собой полный дифференциал некоторой функции, определенной в области G. Иными словами, существует такая функция F (х, у), определенная в G, что 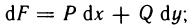
4) в области G всюду 
Доказательство:
Доказательство теоремы проведем по схеме 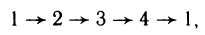
т. е. покажем, что из первого условия следует второе, из второго — третье, из третьего — четвертое, а из четвертого — снова первое. Тем самым будет доказана эквивалентность всех условий.
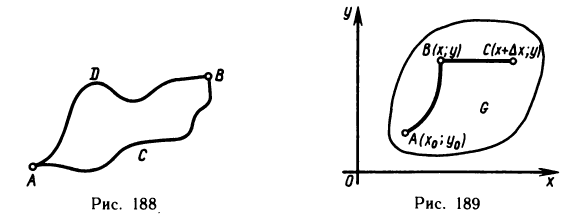
Первый этап: 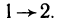 Рассмотрим в области G два произвольных пути, соединяющих точки А и В: АСВ и ADB — любые две кусочно-гладкие кривые (рис. 188). В сумме они составляют замкнутую кривую L=АСВ+BDA, расположенную в G. Согласно условию 1)
Рассмотрим в области G два произвольных пути, соединяющих точки А и В: АСВ и ADB — любые две кусочно-гладкие кривые (рис. 188). В сумме они составляют замкнутую кривую L=АСВ+BDA, расположенную в G. Согласно условию 1)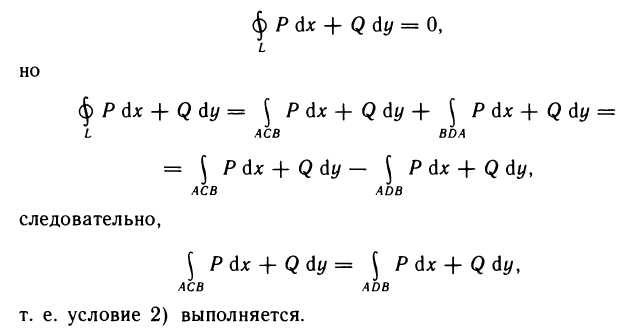
Второй этап:  Пусть интеграл
Пусть интеграл  не зависит от выбора пути интегрирования, а зависит только от точек А и В. Тогда, если точку А зафиксировать:
не зависит от выбора пути интегрирования, а зависит только от точек А и В. Тогда, если точку А зафиксировать:  ,
,
то этот интеграл будет некоторой функцией координат х и у точки В=В(х; у): 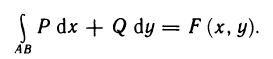
Покажем, что функция F (х, у) дифференцируема и что 
Для этого достаточно доказать, что в каждой точке В области существуют частные производные 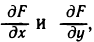 причем
причем 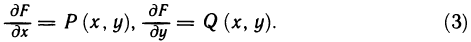
Так как Р (х, у) и Q (х, у) непрерывны в G, то из (3) следует дифференцируемость функции F (х, у) и равенство (2).
Для доказательства существования частной производной функции F (х, у) по х и первого из равенства (3) составим частное приращение по х функции F(х, у) в точке В (х; у): 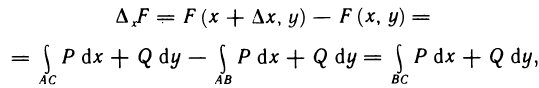 где точка С имеет координаты
где точка С имеет координаты 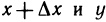 (рис. 189). Так как по условию интеграл не зависит от вида кривой, то возьмем путь от
(рис. 189). Так как по условию интеграл не зависит от вида кривой, то возьмем путь от 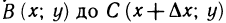 прямолинейным. Тогда
прямолинейным. Тогда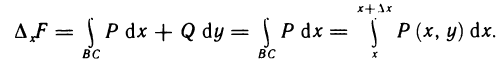
Применяя к последнему интегралу теорему о среднем, получаем 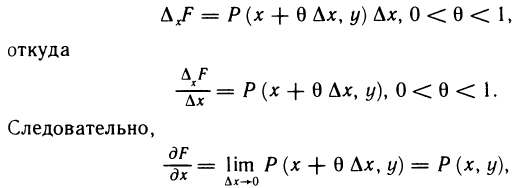 поскольку по условию Р (х, у) непрерывна. Аналогично доказывается, что
поскольку по условию Р (х, у) непрерывна. Аналогично доказывается, что 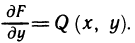 Таким образом, условие 3) установлено.
Таким образом, условие 3) установлено.
Третий этап:  Пусть в области G определена функция F (х, у) такая, что
Пусть в области G определена функция F (х, у) такая, что 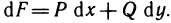 Тогда
Тогда 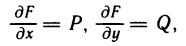
и по теореме о равенстве смешанных производных 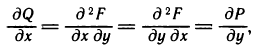
т. е. получено требуемое равенство (1).
Четвертый этап: 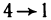 . Пусть выполнено условие 4) и пусть L — кусочно-гладкая кривая, лежащая в области G и ограничивающая область G*. Тогда, применяя формулу Грина к области G* (здесь используется односвязность области G), получаем
. Пусть выполнено условие 4) и пусть L — кусочно-гладкая кривая, лежащая в области G и ограничивающая область G*. Тогда, применяя формулу Грина к области G* (здесь используется односвязность области G), получаем 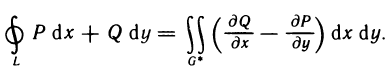
В силу условия 4) интеграл справа равен нулю. Следовательно, 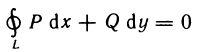
для всякого замкнутого контура L, лежащего в области G.
Замечание:
Из эквивалентности условий 1) — 4) теоремы 13.7, в частности, следует, что условие 3) представляет собой необходимое и достаточное условие, при котором криволинейный интеграл не зависит от выбора пути интегрирования. Однако для приложений более удобным, необходимым и достаточным условием является условие 4).
Теорема 13.7 позволяет легко решать вопрос о том, зависит или не зависит криволинейный интеграл от выбора пути интегрирования. Так, например, 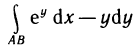 в любой области зависит от выбора пути, так как
в любой области зависит от выбора пути, так как  Необходимо обратить внимание на то, что все условия теоремы существенны. Рассмотрим, например, интеграл
Необходимо обратить внимание на то, что все условия теоремы существенны. Рассмотрим, например, интеграл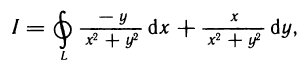
где L — окружность радиуса R с центром в начале координат. Имеем: 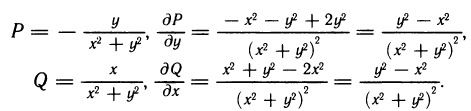
Видим, что условие независимости интеграла от выбора пути формально выполнено, но, однако, интеграл по окружности L нулю не равен. Действительно, задав окружность уравнениями 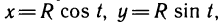 , получим
, получим 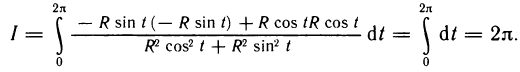
На самом деле никакого противоречия с теоремой здесь нет. Просто не выполнено одно из условий теоремы: функции Р и Q и их частные производные 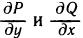 не определены в точке (0; 0), а круг, ограниченный окружностью L, с выброшенной точкой (0; 0) уже не является односвязной областью (начало координат играет роль «дырки»).
не определены в точке (0; 0), а круг, ограниченный окружностью L, с выброшенной точкой (0; 0) уже не является односвязной областью (начало координат играет роль «дырки»).
Интегрирование полных дифференциалов
Из рассмотрения условий независимости криволинейного интеграла 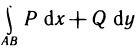 от выбора пути интегрирования непосредственно вытекает решение вопроса об интегрировании полных дифференциалов и о нахождении функции по ее полному дифференциалу.
от выбора пути интегрирования непосредственно вытекает решение вопроса об интегрировании полных дифференциалов и о нахождении функции по ее полному дифференциалу.
Было доказано, что если функции Р (х, у) и Q (x, у) и их частные производные 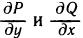 непрерывны в замкнутой области G, то выражение
непрерывны в замкнутой области G, то выражение
является полным дифференциалом некоторой функции в этой области в том и только в том случае, когда 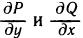 .
.
Далее мы показали, что если это равенство выполнено, то условию 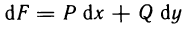
удовлетворяет функция 
Пусть теперь выражение (1) является полным дифференциалом некоторой функции Ф (х, у). Тогда 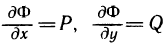 и разность
и разность 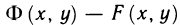 (см. замечание к теореме 12.6) величина постоянная. Следовательно,
(см. замечание к теореме 12.6) величина постоянная. Следовательно, 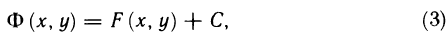
где С — некоторая постоянная. Полагая 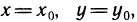 из (2) получаем
из (2) получаем 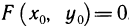 , а из (3)—значение постоянной
, а из (3)—значение постоянной 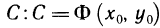 . Теперь (3) можно записать в виде
. Теперь (3) можно записать в виде
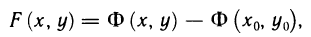
а равенство (2) — в виде 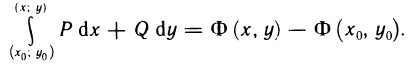
Если, наконец, положить 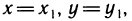 то получим формулу
то получим формулу 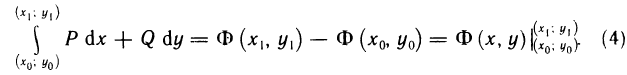
Формула (4) аналогична формуле Ньютона—Лейбница, несправедлива только при условии независимости криволинейного интеграла от выбора пути интегрирования.
Используя полученные результаты, теперь можно указать способ восстановления функции F (х, у), полный дифференциал которой есть заданное выражение (1).
Формула 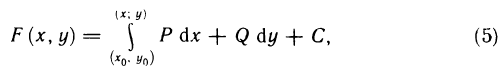
где 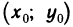 — фиксированная точка, а С — произвольная постоянная, и дает возможность определить все функции, имеющие подынтегральное выражение своим полным дифференциалом.
— фиксированная точка, а С — произвольная постоянная, и дает возможность определить все функции, имеющие подынтегральное выражение своим полным дифференциалом.
Для отыскания F (x, у) по формуле (5) достаточно, выбрав любую точку 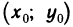 в области G, вычислить криволинейный интеграл по любой кривой, соединяющей точки
в области G, вычислить криволинейный интеграл по любой кривой, соединяющей точки 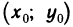 и (х, у). Так как в формуле (5) интеграл не зависит от выбора пути, то удобно, например, за путь интегрирования взять ломаную, звенья которой параллельны осям координат (рис. 190). Тогда
и (х, у). Так как в формуле (5) интеграл не зависит от выбора пути, то удобно, например, за путь интегрирования взять ломаную, звенья которой параллельны осям координат (рис. 190). Тогда 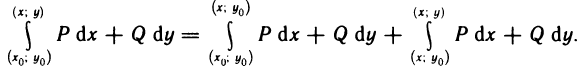
Так как 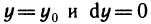 на участке от
на участке от 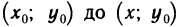 , a dx=0 на участке от
, a dx=0 на участке от 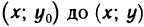 , то равенство (5) принимает вид
, то равенство (5) принимает вид 
где первый определенный интеграл вычисляется при постоянном у, равном 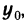 , а второй — при постоянном х.
, а второй — при постоянном х.
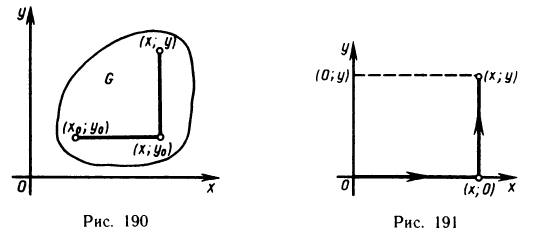
Пример:
Проверить, является ли выражение 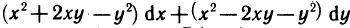 полным дифференциалом некоторой функции F (х, у), и, если это так, найти F (х, у).
полным дифференциалом некоторой функции F (х, у), и, если это так, найти F (х, у).
Решение. В данном выражении функции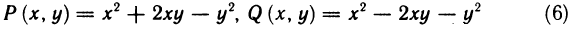 непрерывны вместе с частными производными
непрерывны вместе с частными производными 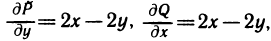 которые равны между собой. Следовательно, данное выражение является полным дифференциалом некоторой функции F (х, у). Для отыскания функции F (х, у) воспользуемся формулой (2), где А
которые равны между собой. Следовательно, данное выражение является полным дифференциалом некоторой функции F (х, у). Для отыскания функции F (х, у) воспользуемся формулой (2), где А 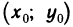 — некоторая фиксированная точка, а В (х; у) — переменная точка.
— некоторая фиксированная точка, а В (х; у) — переменная точка.
В данном случае за точку А 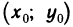 удобно взять точку (0; 0).
удобно взять точку (0; 0).
Учитывая, что криволинейный интеграл 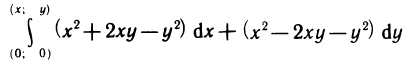 не зависит от пути интегрирования, выберем путь интегрирования от точки (0; 0) до точки (х; у) в виде ломаной, звенья которой параллельны осям координат. Для этого достаточно взять точку (х; 0) [или точку (0; у)] (рис. 191). Тогда одно звено ломаной будет лежать на оси координат. Имеем
не зависит от пути интегрирования, выберем путь интегрирования от точки (0; 0) до точки (х; у) в виде ломаной, звенья которой параллельны осям координат. Для этого достаточно взять точку (х; 0) [или точку (0; у)] (рис. 191). Тогда одно звено ломаной будет лежать на оси координат. Имеем  где С — произвольная постоянная.
где С — произвольная постоянная.
Практически при отыскании функции по ее полному дифференциалу удобно поступать следующим образом. Если 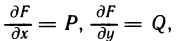
то, интегрируя первое из этих равенств по х, получаем 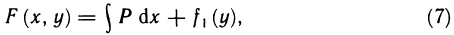
а интегрируя второе равенство по у, имеем 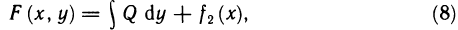
где 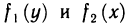 — произвольные функции. Если подобрать функции
— произвольные функции. Если подобрать функции 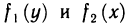 так, чтобы правые части равенств (7) и (8) совпали, то полученная таким образом функция F (x, у) и является функцией, полный дифференциал которой совпадает с выражением
так, чтобы правые части равенств (7) и (8) совпали, то полученная таким образом функция F (x, у) и является функцией, полный дифференциал которой совпадает с выражением 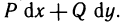
Так, например, пусть 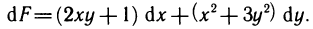 Интегрируя коэффициент при dx по х, получаем
Интегрируя коэффициент при dx по х, получаем 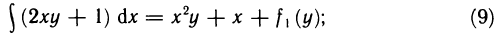
интегрируя коэффициент при dy по у, имеем 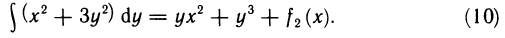
Правые части равенств (9) и (10) совпадают, если положить 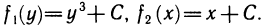 Таким образом,
Таким образом, 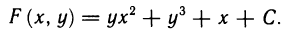
Пример:
Вычислить криволинейный интеграл 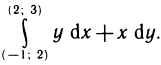
Решение:
В данном случае функции 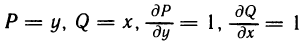
непрерывны и частные производные равны между собой. Значит, выражение уdх+хdу является полным дифференциалом dF (х, у) и данный интеграл не зависит от пути интегрирования. По формулам (7) и (8) находим F (х, у)=ху, и по формуле (4) получаем 
Заметим, что данный интеграл можно вычислить и непосредственно, если, например, взять в качестве пути интегрирования ломаную, соединяющую точки (— 1; 2), (2; 2) и (2; 3), звенья которой параллельны осям координат (проделайте самостоятельно).
Некоторые приложения криволинейных интегралов второго рода
Криволинейные интегралы второго рода, так же как и первого рода, имеют широкое применение в геометрии, физике и технике. Ограничимся рассмотрением двух задач: вычислением площадей плоских фигур и определением работы силы.
Вычисление площади с помощью формулы Грина
Пусть G — некоторая область с границей L и s — площадь этой области. Известно, что двойной интеграл 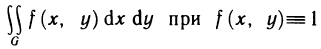
выражает площадь области G. Поэтому если в формуле Грина подобрать функции Р(х,у) и Q(x,y) таким образом, чтобы 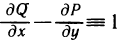 , то площадь s области G определяется формулой
, то площадь s области G определяется формулой 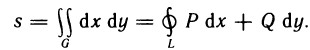
Положим 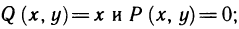 тогда
тогда 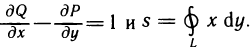
Полагая 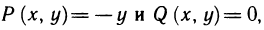 аналогично находим
аналогично находим 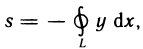
а при 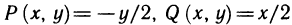 имеем
имеем 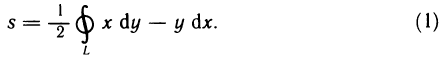
Таким образом, получены три формулы для вычисления площадей плоских фигур, ограниченных контуром L.
Пример:
Найти площадь фигуры, ограниченной эллипсом. Решение. Вычислим, например, площадь по формуле (1). Используя параметрические уравнения эллипса 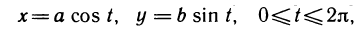 имеем
имеем 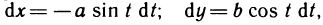 по формуле (1) получаем
по формуле (1) получаем 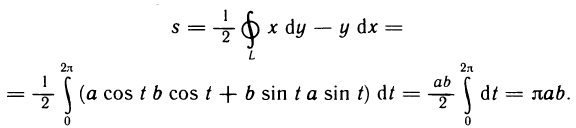
Работа силы
Известно, что работа, совершаемая переменной силой F (х), направленной вдоль оси Ох, по перемещению материальной точки вдоль оси Ох из точки х=а в точку 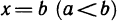 определяется с помощью определенного интеграла по формуле
определяется с помощью определенного интеграла по формуле 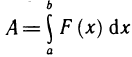
(гл. 6, § 8, п. 6). Рассмотрим более общую задачу.
Пусть материальная точка под действием силы  перемещается вдоль непрерывной плоской кривой ВС в направлении от В к С. Сила
перемещается вдоль непрерывной плоской кривой ВС в направлении от В к С. Сила  предполагается переменной, зависящей от положения точки на кривой ВС. Вычислим работу силы
предполагается переменной, зависящей от положения точки на кривой ВС. Вычислим работу силы  при перемещении точки из В в С. Для этого разобьем (рис. 192) произвольно кривую ВС на n частей точками
при перемещении точки из В в С. Для этого разобьем (рис. 192) произвольно кривую ВС на n частей точками  Заменим приближенно на участке
Заменим приближенно на участке  силу F постоянным значением, равным ее значению в точке
силу F постоянным значением, равным ее значению в точке  а движение точки по дуге
а движение точки по дуге 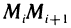 заменим движением по отрезку
заменим движением по отрезку 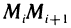 . Тогда работу постоянной силы
. Тогда работу постоянной силы 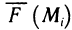 вдоль отрезка
вдоль отрезка  можно принять за приближенное значение работы
можно принять за приближенное значение работы  переменной силы F вдоль дуги
переменной силы F вдоль дуги 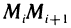 т. е.
т. е. 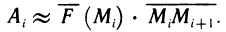
Правая часть этого приближенного равенства представляет собой скалярное произведение двух векторов 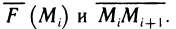 Оно равно сумме произведений соответствующих координат этих векторов, т. е. если
Оно равно сумме произведений соответствующих координат этих векторов, т. е. если 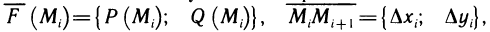 то
то 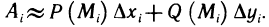 Суммируя по всем значениям i от 1 до n, получаем приближенное значение работы А вдоль всей кривой ВС:
Суммируя по всем значениям i от 1 до n, получаем приближенное значение работы А вдоль всей кривой ВС: 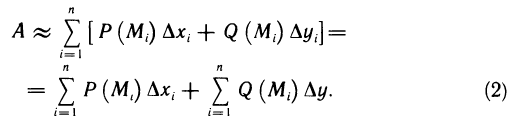
За точное значение работы А принимается предел, к которому стремится ее приближенное значение при стремлении к нулю наибольшей из длин дуг 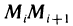 . Но, с другой стороны, сумма (2) представляет собой сумму двух интегральных сумм для функций
. Но, с другой стороны, сумма (2) представляет собой сумму двух интегральных сумм для функций
Р (х, у) и Q (х, у), заданных на кривой ВС. По определению пределом этой суммы является криволинейный интеграл второго рода.
Следовательно, работа силы определяется по формуле 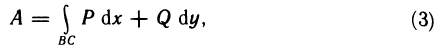
где Р и Q — координаты (или проекции на оси координат) силы  .
.
Если рассмотреть данную задачу не на плоскости, а в пространстве, то решение ее сводится к вычислению криволинейного интеграла второго рода по пространственной кривой по формуле 
Пример:
Вычислить работу силы  (х; у) при перемещении материальной точки по эллипсу в положительном направлении, если сила в каждой точке (x; у) эллипса направлена к центру эллипса и по величине равна расстоянию от точки (х; у) до центра эллипса (рис. 193).
(х; у) при перемещении материальной точки по эллипсу в положительном направлении, если сила в каждой точке (x; у) эллипса направлена к центру эллипса и по величине равна расстоянию от точки (х; у) до центра эллипса (рис. 193).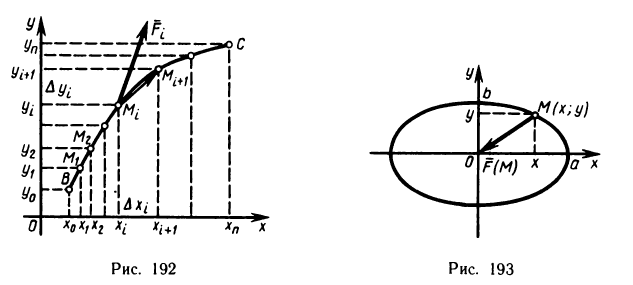
Решение:
По условию, 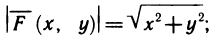 координаты силы
координаты силы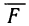 (х, у) таковы:
(х, у) таковы: 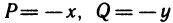 [знак «—» объясняется тем, что сила направлена к точке (0; 0)]. По формуле (3) имеем
[знак «—» объясняется тем, что сила направлена к точке (0; 0)]. По формуле (3) имеем 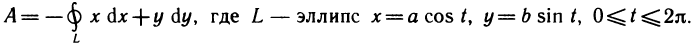
Следовательно, 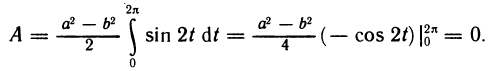
Заметим, что из того, что интеграл оказался равным нулю, следует, что подынтегральное выражение является полным дифференциалом некоторой функции (найдите эту функцию самостоятельно).
Тройные интегралы
В начале главы было введено понятие двойного интеграла от функции двух переменных. Определим интеграл от функции трех переменных — так называемый тройной интеграл. Тройные интегралы, как и двойные, имеют широкое применение в различных физических и геометрических задачах.
Определение тройного интеграла
Тройной интеграл является аналогом двойного интеграла и вводится для функции трех переменных.
Пусть в некоторой замкнутой ограниченной области V трехмерного пространства задана ограниченная функция 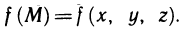 Разобьем область V на n произвольных областей, не имеющих общих внутренних точек, с объемами
Разобьем область V на n произвольных областей, не имеющих общих внутренних точек, с объемами 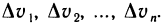
В каждой области возьмем произвольную точку 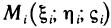 и составим сумму
и составим сумму 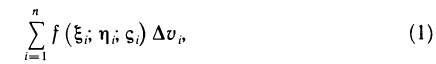
которая называется интегральной суммой для функции f (x, у, z) по области V. Обозначим через 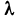 наибольший из диаметров частичных областей.
наибольший из диаметров частичных областей.
Определение:
Если интегральная сумма (1) при  имеет предел, равный I, то этот предел называется тройным интегралом от функции f (x, у, z) по области V и обозначается одним из следующих символов:
имеет предел, равный I, то этот предел называется тройным интегралом от функции f (x, у, z) по области V и обозначается одним из следующих символов: 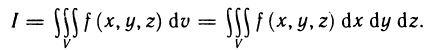
В этом случае функция f (x, у, z) называется интегрируемой в области V; V — областью интегрирования; х, у и z — переменными интегрирования; 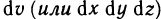 — элементом объема.
— элементом объема.
В дальнейшем, поскольку результаты, полученные для двойных интегралов, вместе с их доказательствами могут быть перенесены на тройные интегралы, ограничимся только формулировками утверждений и краткими пояснениями.
Тройные интегралы являются непосредственным обобщением двойных интегралов на случай трехмерного пространства. Они обладают аналогичными двойным интегралам необходимыми и достаточными условиями существования и свойствами. Если положить всюду в области 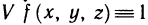 , то из определения тройного интеграла следует формула для вычисления объема тела V:
, то из определения тройного интеграла следует формула для вычисления объема тела V: 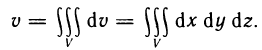
Вычисление тройных интегралов
Как и в случае двойных интегралов, вычисление тройных интегралов сводится к вычислению интегралов меньшей кратности.
Рассмотрим область V, ограниченную снизу и сверху поверхностями 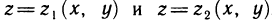 , а с боковых сторон цилиндрической поверхностью, и пусть область G — проекция области V на плоскость Оху (рис. 194), в которой определены и непрерывны функции
, а с боковых сторон цилиндрической поверхностью, и пусть область G — проекция области V на плоскость Оху (рис. 194), в которой определены и непрерывны функции 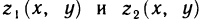 . Предположим, далее, что каждая прямая, параллельная оси Oz, пересекает границу области V не более чем в двух точках. Тогда для любой функции f (x, у, z), непрерывной в области V, имеет место формула
. Предположим, далее, что каждая прямая, параллельная оси Oz, пересекает границу области V не более чем в двух точках. Тогда для любой функции f (x, у, z), непрерывной в области V, имеет место формула 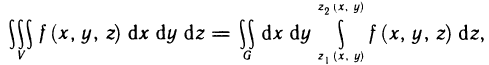
позволяющая свести вычисление тройного интеграла к последовательному вычислению внутреннего определенного интеграла по переменной z (при постоянных х и у) и внешнего двойного интеграла по области G.
Выражение 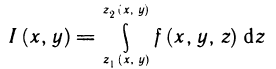
представляет собой функцию двух переменных. Если для этой функции и области G, по которой она интегрируется, выполнены условия теоремы 13.4, то, переходя от двойного интеграла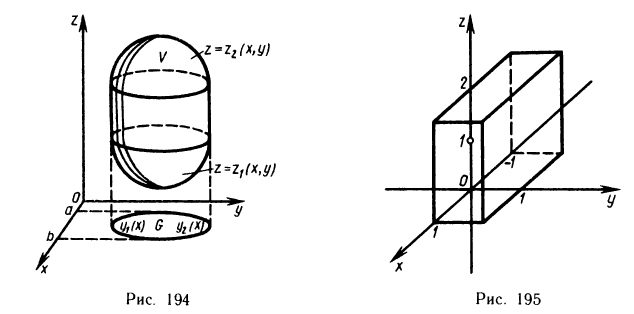
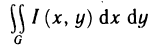 к повторному, получаем формулу
к повторному, получаем формулу 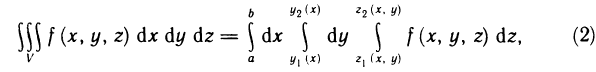 сводящую вычисление тройного интеграла к последовательному вычислению трех определенных интегралов. Порядок интегрирования может быть и другим, т. е. переменные х, у и z в формуле (2) можно менять ролями.
сводящую вычисление тройного интеграла к последовательному вычислению трех определенных интегралов. Порядок интегрирования может быть и другим, т. е. переменные х, у и z в формуле (2) можно менять ролями.
В частности, если V— параллелепипед с гранями 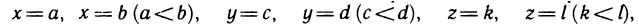 то формула (2) принимает вид
то формула (2) принимает вид 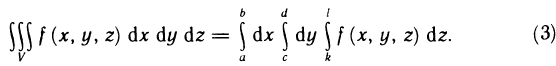
В этом случае интегрирование можно производить в любом порядке.
Пример:
Вычислить интеграл 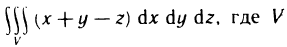 — параллелепипед, ограниченный плоскостями
— параллелепипед, ограниченный плоскостями 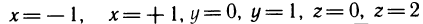 (рис. 195).
(рис. 195).
Решение. По формуле (3) имеем 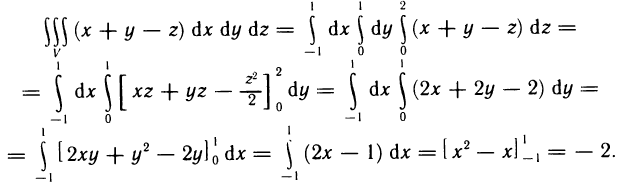
Пример:
Вычислить интеграл 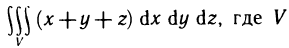 —пирамида, ограниченная плоскостью x+y+z=1 и координатными плоскостями х=0, у=0, z=0 (рис. 196).
—пирамида, ограниченная плоскостью x+y+z=1 и координатными плоскостями х=0, у=0, z=0 (рис. 196).
Решение. Область V проектируется на плоскость Оху в треугольник G, ограниченный прямыми х=0 у=0, у=1-х. По формуле (2) имеем 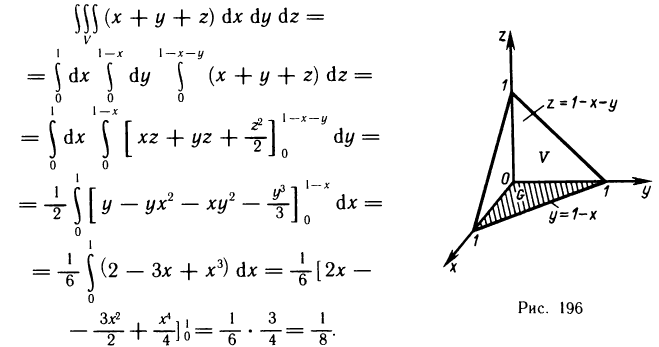
Замена переменных в тройном интеграле
Как для двойных интегралов, так и для тройных имеют место формулы перехода от прямоугольных координат к новым системам координат, наиболее употребительными из которых являются цилиндрические и сферические координаты.
Замену переменных в тройном интеграле производят по следующему правилу.
Если ограниченная замкнутая область V пространства (х, у, z) взаимно однозначно отображается на область V* пространства 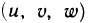 с помощью непрерывно дифференцируемых функций
с помощью непрерывно дифференцируемых функций 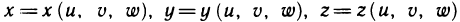 и якобы J в области V* не обращается в нуль:
и якобы J в области V* не обращается в нуль: 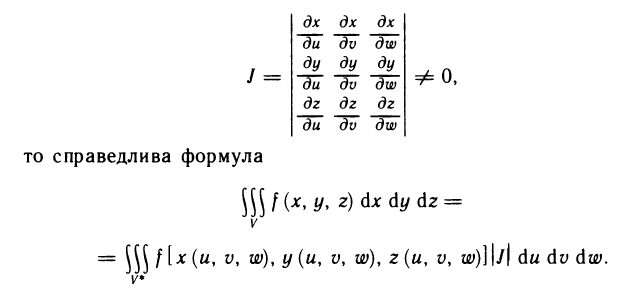
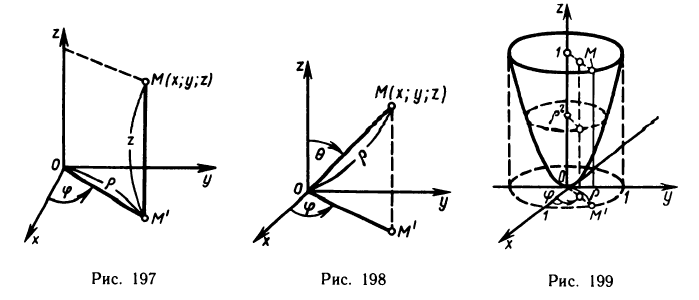
В частности, при переходе от прямоугольных координат х, у, z к цилиндрическим координатам 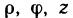 (рис. 197), связанным с х, у, z формулами
(рис. 197), связанным с х, у, z формулами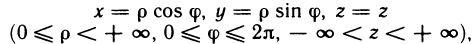
якобиан преобразования J=р, поэтому 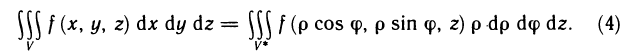
Название цилиндрические координаты связано с тем, что координатная поверхность p=const (т. е. поверхность, все точки которой имеют одну и ту же координату р) является цилиндром, прямолинейные образующие которого параллельны оси Oz.
При переходе от прямоугольных координат х, у, z к сферическим координатам 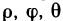 (рис. 198), связанным с х, у, z формулами
(рис. 198), связанным с х, у, z формулами 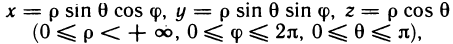
якобиан преобразования 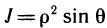 , поэтому
, поэтому 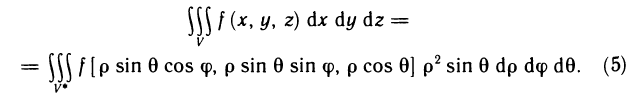
Название «сферические координаты» связано с тем, что координатная поверхность р=const (т. е. поверхность, все точки которой имеют одну и ту же координату р) является сферой. Сферические координаты иначе.- называют полярными координатами в пространстве.
При вычислении тройного интеграла путем перехода к цилиндрическим или сферическим координатам область V* обычно не изображают, а пределы интегрирования расставляют непосредственно по виду области V, используя геометрический смысл новых координат.
Пример:
Вычислить интеграл 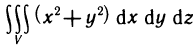 переходом к цилиндрическим координатам
переходом к цилиндрическим координатам 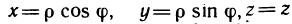 где V — область, ограниченная поверхностями
где V — область, ограниченная поверхностями 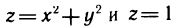 (рис. 199).
(рис. 199).
Решение:
Так как область V на плоскость Оху проектируется в круг 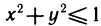 , то координата
, то координата  изменяется в пределах от
изменяется в пределах от  , координата
, координата 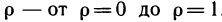 . Постоянному значению
. Постоянному значению 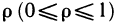 в пространстве Охуz соответствует цилиндр
в пространстве Охуz соответствует цилиндр 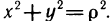 Рассматривая пересечение этого цилиндра с областью V, получаем изменение координаты z от значений для точек, лежащих на параболоиде
Рассматривая пересечение этого цилиндра с областью V, получаем изменение координаты z от значений для точек, лежащих на параболоиде 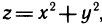 , до значений для точек, лежащих на плоскости
, до значений для точек, лежащих на плоскости 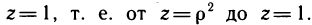 Применяя формулу (4), имеем
Применяя формулу (4), имеем 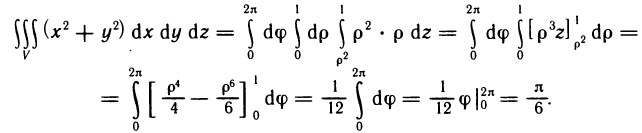
Трудно дать какую-либо общую рекомендацию, когда следует применять ту или иную систему координат. Это зависит и от области интегрирования, и от вида подынтегральной функции. Однако, например, формулой (5) удобнее пользоваться, когда f (х, у, г.z) имеет вид 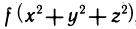 , а также когда областью V является шар
, а также когда областью V является шар 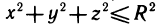 или его часть.
или его часть.
Пример:
Вычислить интеграл 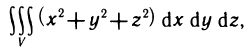 где V— шар
где V— шар 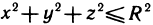 (рис. 200).
(рис. 200).
Решение:
В данном случае удобно перейти к сферическим координатам:  . Из вида области V следует, что координаты
. Из вида области V следует, что координаты 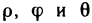 меняются в следующих пределах:
меняются в следующих пределах: 
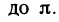 Так как подынтегральная функция
Так как подынтегральная функция 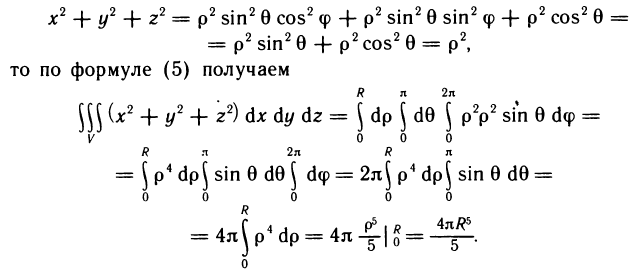
Некоторые приложения тройных интегралов
Кратко рассмотрим типичные задачи применения тройных интегралов, ограничившись приведением необходимых формул, так как их вывод аналогичен выводу соответствующих формул в случае двойных интегралов.
Если дано некоторое тело V с плотностью p(M)=p(x, у, z), представляющей собой непрерывную функцию, то тройной интеграл 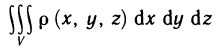
представляет собой массу m данного тела.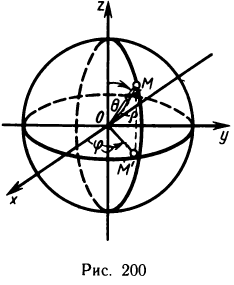
Моменты инерции тела V с плотностью р(М)=р(x, у, z) относительно осей координат определяются следующими формулами: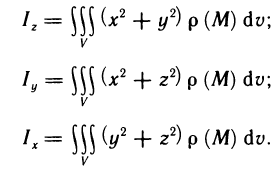
Момент инерции относительно начала координат 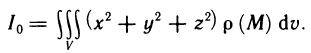
Координаты центра масс определяются следующими формулами: 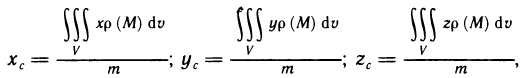 где
где 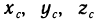 — координаты центра масс, а m — масса данного тела. В частности, если рассматриваемое тело однородно, т. е.
— координаты центра масс, а m — масса данного тела. В частности, если рассматриваемое тело однородно, т. е.
р (х, у, z)=const, то выражения для координат центра масс упрощаются и принимают вид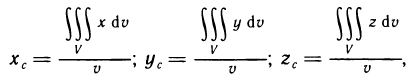
где 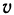 — объем данного тела.
— объем данного тела.
Как уже было отмечено, тройной интеграл 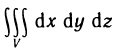 равен объему тела V.
равен объему тела V.
Тройные интегралы в некоторых случаях более удобны для вычисления объемов, чем двойные, так как с их помощью можно вычислить объем не только криволинейного цилиндра, но и других тел.
Пример:
Определить координаты центра масс верхней половины однородного шара V радиуса R с центром в начале координат.
Решение:
Данный полушар ограничен поверхностями 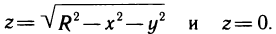 В силу симметрии полушара
В силу симметрии полушара 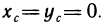 Координата
Координата  определяется по формуле
определяется по формуле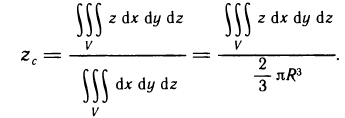
Переходя к сферическим координатам, получаем 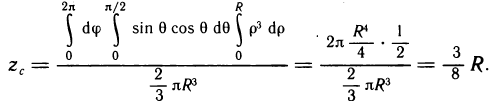
Поверхностные интегралы
В этом параграфе рассмотрены интегралы от функций, заданных на поверхности, так называемые поверхностные интегралы.
Теория поверхностных интегралов во многом аналогична теории криволинейных интегралов. Различают поверхностные интегралы первого и второго рода.
Определение поверхностного интеграла первого рода
Пусть в точках некоторой поверхности S гладкой или кусочно-гладкой определена ограниченная функция 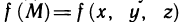 . Разобьем поверхность S произвольно на n частей с площадями
. Разобьем поверхность S произвольно на n частей с площадями 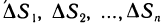 (рис. 201). Выбрав на каждой частичной поверхности произвольную точку
(рис. 201). Выбрав на каждой частичной поверхности произвольную точку 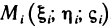 составим сумму
составим сумму 
Сумма (1) называется интегральной суммой для функции f (M) по поверхности S. Обозначим через  наибольший из диаметров частей поверхности.
наибольший из диаметров частей поверхности.
Определение:
Если интегральная сумма (1) при  имеет предел, равный I, то этот предел называется поверхностным интегралом первого рода от функции f (х, у, z) по поверхности S и обозначается одним из следующих символов:
имеет предел, равный I, то этот предел называется поверхностным интегралом первого рода от функции f (х, у, z) по поверхности S и обозначается одним из следующих символов: 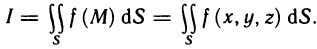
В этом случае функция f (х, у, z) называется интегрируемой по поверхности S, S — областью интегрирования.
Данное определение по сути аналогично определению двойного интеграла. Поэтому свойства двойных интегралов и условия их существования без особых изменений переносятся на поверхностные интегралы.
В частности, если  на поверхности S, то
на поверхности S, то 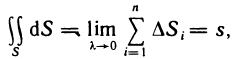
где s — площадь поверхности S, т. е. с помощью поверхностного интеграла первого рода можно вычислять площади поверхностей.
Кроме того, с их помощь!о можно определять массы, статические моменты, моменты инерции, координаты центра масс и подобные величины для материальных поверхностей с известной поверхностной плотностью распределения масс. Эти задачи решаются аналогично соответствующим задачам для случая материальной кривой, материальной плоской и пространственной области.
Вычисление поверхностных интегралов первого рода
Вычисление поверхностного интеграла первого рода производится сведением поверхностного интеграла к двойному.
Пусть поверхность S задана уравнением z=z(x, у), где функция z(x, у) вместе с производными 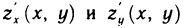 непрерывна в замкнутой области G — проекции S на плоскость Оху (рис. 202), и пусть функция f (х, у, z) непрерывна на поверхности S и, следовательно, интегрируема по этой поверхности.
непрерывна в замкнутой области G — проекции S на плоскость Оху (рис. 202), и пусть функция f (х, у, z) непрерывна на поверхности S и, следовательно, интегрируема по этой поверхности.
Разобьем поверхность S произвольно на n частей и спроектируем это разбиение на плоскость Оху. Получим соответственно разбиение области G на части  Площадь
Площадь 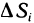 каждой части поверхности может быть представлена в виде (см. формулу (2), п. 3, § 4)
каждой части поверхности может быть представлена в виде (см. формулу (2), п. 3, § 4) 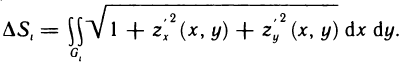
Применяя к двойному интегралу теорему о среднем, получаем 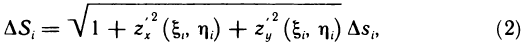
где  — некоторая точка области G,; As, — площадь G,. Обозначим через М, точку на частичной поверхности с координатами
— некоторая точка области G,; As, — площадь G,. Обозначим через М, точку на частичной поверхности с координатами  — точка, которая имеется в формуле (2). Составим интегральную сумму для функции f (x, y, z) по поверхности S, выбирая точки
— точка, которая имеется в формуле (2). Составим интегральную сумму для функции f (x, y, z) по поверхности S, выбирая точки 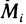 в качестве промежуточных:
в качестве промежуточных: 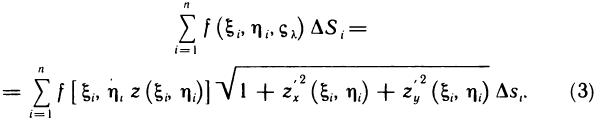
В правой части равенства находится интегральная сумма для двойного интеграла от непрерывной в области G функции 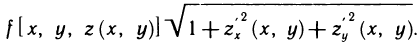 Поэтому предел правой части (3) при
Поэтому предел правой части (3) при  равен двойному интегралу
равен двойному интегралу 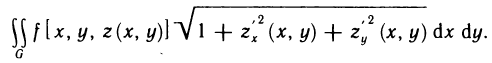
Так как функция f (x, у, z) интегрируема по поверхности S, то предел левой части (3) при  равен поверхностному интегралу
равен поверхностному интегралу 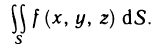
Следовательно, переходя к пределу в (3) при  , получаем искомую формулу
, получаем искомую формулу 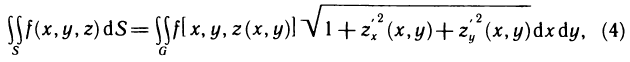 выражающую поверхностный интеграл первого рода через двойной по проекции поверхности S на плоскость Оху.
выражающую поверхностный интеграл первого рода через двойной по проекции поверхности S на плоскость Оху.
Аналогично получаются формулы, выражающие интеграл по поверхности S через двойные по ее проекциям на плоскости Оуz и Oxz.
Пример:
Вычислить интеграл 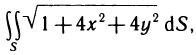 где S — часть параболоида вращения
где S — часть параболоида вращения 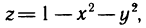 отсеченного плоскостью z=0 (рис. 203).
отсеченного плоскостью z=0 (рис. 203).
Решение. Поверхность S, заданная уравнением 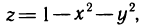 проектируется на плоскость Оху в область G, ограниченную окружностью
проектируется на плоскость Оху в область G, ограниченную окружностью  (уравнение окружности получается из уравнения параболоида при z=0).
(уравнение окружности получается из уравнения параболоида при z=0).
Следовательно, областью G является круг  В этом круге функции
В этом круге функции 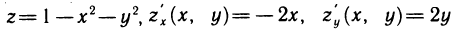 непрерывны. По формуле (4) получаем
непрерывны. По формуле (4) получаем 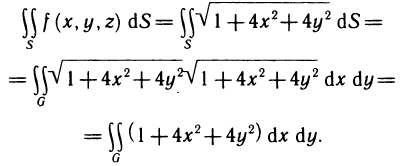
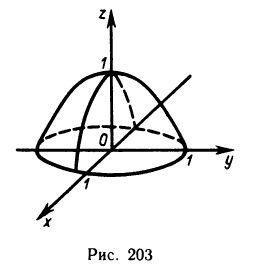
Переходя в полученном двойном интеграле к полярным координатам 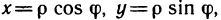 находим
находим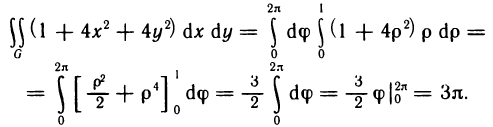
Определение поверхностного интеграла второго рода
Введем предварительно понятие стороны поверхности.
Возьмем на гладкой поверхности S произвольную точку М и проведем через нее нормаль к поверхности (вектор 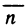 ). Рассмотрим теперь на поверхности S какой-либо замкнутый контур, проходящий через точку М и не имеющий общих точек с границей поверхности S. Будем перемещать точку М по замкнутому контуру вместе с вектором
). Рассмотрим теперь на поверхности S какой-либо замкнутый контур, проходящий через точку М и не имеющий общих точек с границей поверхности S. Будем перемещать точку М по замкнутому контуру вместе с вектором 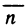 так, чтобы вектор
так, чтобы вектор 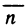 все время оставался нормальным к S и чтобы его направление менялось при этом перемещении непрерывно (рис. 204). В начальное положение точка М вернется либо с тем же направлением нормали, либо с противоположным.
все время оставался нормальным к S и чтобы его направление менялось при этом перемещении непрерывно (рис. 204). В начальное положение точка М вернется либо с тем же направлением нормали, либо с противоположным.
Если обход по любому замкнутому контуру, лежащему на поверхности S и не пересекающему ее границы, при возвращении в исходную точку не меняет направления нормали к поверхности, то поверхность называется двусторонней.
Примерами двусторонних поверхностей служат плоскость, сфера, любая поверхность, заданная уравнением z=f (x, у), где 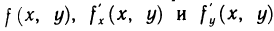 — функции, непрерывные в некоторой области G плоскости Оху.
— функции, непрерывные в некоторой области G плоскости Оху.
Если же на поверхности S существует замкнутый контур, при обходе которого направление нормали меняется после возвращения в исходную точку на противоположное, то поверхность называется односторонней.
Простейшим примером односторонней поверхности служит лист Мёбиуса, изображенный на рис. 205. Его можно получить, взяв полоску бумаги ABCD и склеив ее так, чтобы точка А совпала с точкой С, а точка В — с точкой D, т. е. повернув перед склеиванием один из ее краев на 180°. При обходе листа Мёбиуса по его средней линии и возвращении в исходную точку направление нормали меняется на противоположное.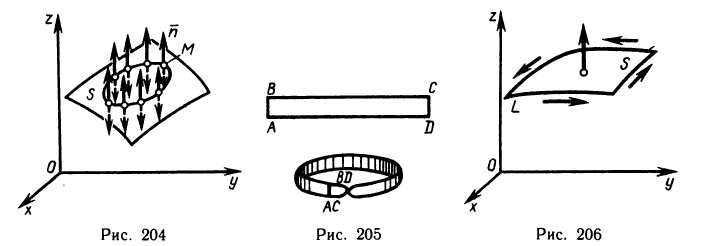
В дальнейшем рассматриваются только двусторонние поверхности. Для двусторонней поверхности совокупность всех ее точек с выбранным в них направлением нормали, изменяющимся непрерывно при переходе от точки к точке, называется стороной поверхности, а выбор определенной ее стороны — ориентацией поверхности. Двустороннюю поверхность называют также ориентируемой, а одностороннюю — неориентируемой.
С понятием стороны поверхности тесно связано понятие ориентации ее границы.
Пусть S — ориентированная (сторона уже выбрана) поверхность, ограниченная контуром L, не имеющим точек самопересечения. Будем считать положительным направлением обхода контура L то, при движении по которому наблюдатель, расположенный так, что направление нормали совпадает с направлением от ног к голове, оставляет поверхность слева от себя (рис. 206). Противоположное направление обхода называется отрицательным. Если изменить ориентацию поверхности, т. е. изменить направление нормали на противоположное, то положительное и отрицательное направления обхода контура L поменяются ролями.
Перейдем теперь к определению поверхностного интеграла второго рода.
Пусть S — гладкая поверхность, заданная уравнением  — ограниченная функция, определенная в точках поверхности S. Выберем одну из двух сторон поверхности, т. е. одно из двух возможных направлений нормали в точках поверхности (тем самым мы ориентировали поверхность). Если нормали составляют острые углы с осью Оz, то будем говорить, что выбрана верхняя сторона поверхности z=f(x, у), если тупые углы, то нижняя сторона поверхности. Разобьем поверхность S произвольно на п частей и обозначим через
— ограниченная функция, определенная в точках поверхности S. Выберем одну из двух сторон поверхности, т. е. одно из двух возможных направлений нормали в точках поверхности (тем самым мы ориентировали поверхность). Если нормали составляют острые углы с осью Оz, то будем говорить, что выбрана верхняя сторона поверхности z=f(x, у), если тупые углы, то нижняя сторона поверхности. Разобьем поверхность S произвольно на п частей и обозначим через  проекцию i-й части поверхности на плоскость Оху. Выбрав на каждой частичной поверхности произвольную точку
проекцию i-й части поверхности на плоскость Оху. Выбрав на каждой частичной поверхности произвольную точку 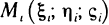 , составим сумму
, составим сумму

где 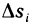 — площадь
— площадь 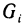 взятая со знаком плюс, если выбрана верхняя сторона поверхности S, и со знаком минус, если выбрана нижняя сторона поверхности S. Сумма (5) называется интегральной суммой для функции R(M)=R(x, у, z). Обозначим через А. наибольший из диаметров частей поверхности S.
взятая со знаком плюс, если выбрана верхняя сторона поверхности S, и со знаком минус, если выбрана нижняя сторона поверхности S. Сумма (5) называется интегральной суммой для функции R(M)=R(x, у, z). Обозначим через А. наибольший из диаметров частей поверхности S.
Определение:
Если интегральная сумма (5) при  имеет предел, равный I, то этот предел называется поверхностным интегралом второго рода от функции R (х, у, z) по выбранной стороне поверхности S и обозначается одним из следующих символов:
имеет предел, равный I, то этот предел называется поверхностным интегралом второго рода от функции R (х, у, z) по выбранной стороне поверхности S и обозначается одним из следующих символов: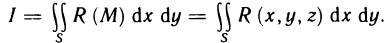
В этом случае функция R (х, у, z) называется интегрируемой по поверхности S по переменным х и у.
Аналогично определяется поверхностный интеграл второго рода по выбранной стороне поверхности S по переменным у и z [z и x] от функции 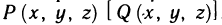 , которая определена на поверхности S:
, которая определена на поверхности S: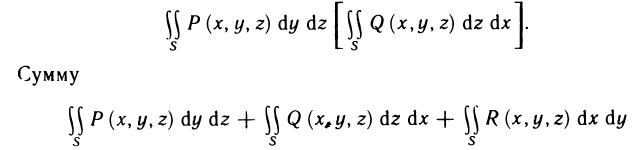
называют общим поверхностным интегралом второго рода и обозначают символом 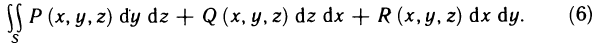
Поверхностный интеграл второго рода обладает такими же свойствами, как и поверхностный интеграл первого рода, но в отличие от последнего при изменении стороны поверхности (переориентации) он меняет знак.
К понятию поверхностного интеграла второго рода приводит, например, задача о потоке векторного поля, которая будет рассмотрена в $ 14.
Для односторонней поверхности понятие поверхностного интеграла второго рода не вводится.
Вычисление поверхностных интегралов второго рода
Поверхностные интегралы второго рода вычисляют сведением их к двойным интегралам.
Пусть ориентированная (выберем верхнюю сторону) гладкая поверхность S задана уравнением z=f( x, у), где функция f (x, у) определена в замкнутой области G — проекции поверхности S на плоскость Оху, a R (х, у, z) — непрерывная функция на поверхности S.
Разобьем поверхность S произвольно на п частей и спроектируем это разбиение на плоскость Оху (рис. 207). Область G разобьется соответственно на части  Выберем на каждой части поверхности произвольную точку
Выберем на каждой части поверхности произвольную точку 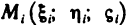 и составим интегральную сумму
и составим интегральную сумму 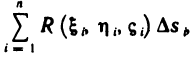
где  — площадь
— площадь  . Так как
. Так как 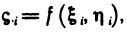 то
то 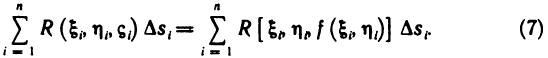
В правой части равенства находится интегральная сумма для двойного интеграла от непрерывной в области G функции
R [x, у, f(x, у)]. Переходя к пределу в (7) при  , получаем искомую формулу
, получаем искомую формулу 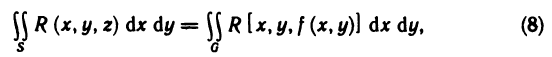 выражающую поверхностный интеграл второго рода по переменным х и у через двойной. Кроме того, формула (8) доказывает существование поверхностного интеграла от функции R (х, у, z), непрерывной на рассматриваемой поверхности S. Если выбрать нижнюю сторону поверхности, то перед интегралом в правой части (8) появится знак минус.
выражающую поверхностный интеграл второго рода по переменным х и у через двойной. Кроме того, формула (8) доказывает существование поверхностного интеграла от функции R (х, у, z), непрерывной на рассматриваемой поверхности S. Если выбрать нижнюю сторону поверхности, то перед интегралом в правой части (8) появится знак минус.
Аналогично устанавливается справедливость следующих формул: 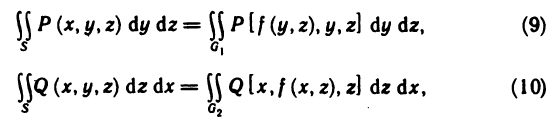
где поверхность S задана соответственно уравнением x=f(y, z) и
y=f(x, z), a 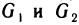 —проекции поверхности S соответственно на плоскости Оуz и Oxz.
—проекции поверхности S соответственно на плоскости Оуz и Oxz.
Для вычисления интеграла общего вида (6) используют те же формулы (8) — (10), если поверхность S однозначно проектируется на все три координатные плоскости. В более сложных случаях поверхность S разбивают на части, обладающие указанными свойствами, а интеграл (6) — на сумму интегралов по этим частям.
Пример:
Вычислить интеграл  где S — верхняя сторона поверхности
где S — верхняя сторона поверхности  отсеченная плоскостями у=0, у=1 (рис. 208).
отсеченная плоскостями у=0, у=1 (рис. 208).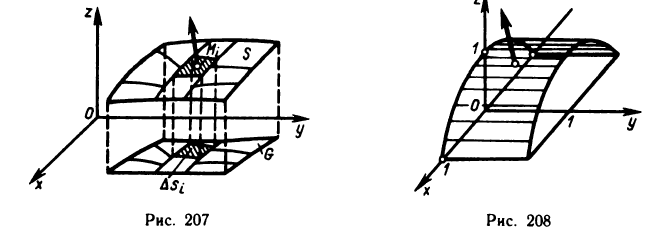
Решение:
Проекцией G данной поверхности на плоскость Оху является прямоугольник, определяемый неравенствами 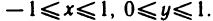 По формуле (8) находим
По формуле (8) находим 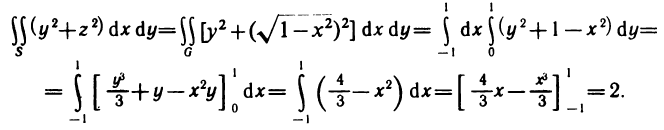
Пример:
Вычислить интеграл 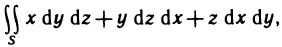 где S — верхняя сторона части плоскости x+z-1=0, отсеченная плоскостями
где S — верхняя сторона части плоскости x+z-1=0, отсеченная плоскостями
у=0, у=4 и лежащая в первом октанте (рис. 209).
Решение:
По определению, 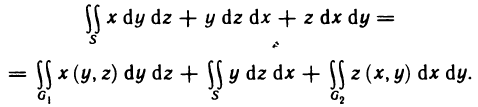
Здесь  — проекции поверхности S на плоскости Oyz и Оху, а
— проекции поверхности S на плоскости Oyz и Оху, а 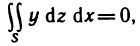
так как плоскость S параллельна оси Оу. По формулам (8) и (9) соответственно находим 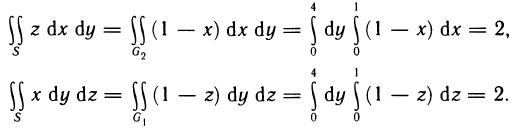
Следовательно, 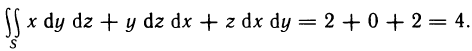
Связь между поверхностными интегралами первого и второго рода
Поверхностные интегралы второго рода можно ввести и другим способом, а именно как поверхностные интегралы первого рода, в которых под знаком интеграла стоят некоторые специальные выражения. Обозначим через  направляющие косинусы нормали ориентированной поверхности в произвольной ее точке. Поверхностные интегралы второго рода различаются своим отношением к координатным плоскостям:
направляющие косинусы нормали ориентированной поверхности в произвольной ее точке. Поверхностные интегралы второго рода различаются своим отношением к координатным плоскостям: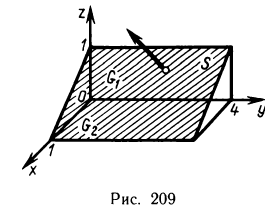
1. поверхностный интеграл второго рода для плоскости Оху от функции R(x, у, z) выражается через поверхностный интеграл первого рода с помощью следующей формулы: 
2. поверхностный интеграл второго рода для плоскости Oxz от функции Q (х, у, z) выражается через поверхностный интеграл первого рода с помощью следующей формулы: 
3. поверхностный интеграл второго рода для плоскости Oyz от функции Р(х, у, z) выражается через поверхностный интеграл первого рода с помощью следующей формулы: 
Суммируя формулы (11) — (13), получаем формулу, выражающую поверхностный интеграл второго рода общего вида по выбранной стороне поверхности через поверхностный интеграл первого рода: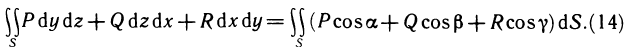
Если выбрать другую сторону поверхности, то направляющие косинусы нормали 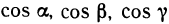 изменят знак и, следовательно, изменит знак поверхностный интеграл второго рода.
изменят знак и, следовательно, изменит знак поверхностный интеграл второго рода.
Пример:
Вычислить интеграл 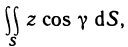 где S — внешняя сторона полусферы
где S — внешняя сторона полусферы 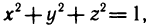 расположенной над плоскостью Оху, а
расположенной над плоскостью Оху, а 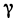 — острый угол между нормалью к поверхности S с осью Oz (рис. 210).
— острый угол между нормалью к поверхности S с осью Oz (рис. 210).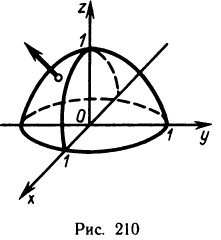
Решение:
По формуле (11), связывающей поверхностные интегралы обоих типов, имеем 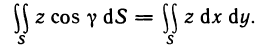
Проекцией G данной поверхности S на плоскость Оху является круг  . По формуле (8) получаем
. По формуле (8) получаем 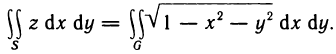
Переходя в двойном интеграле к полярным координатам, находим 
Формула Остроградского
Формула Остроградского устанавливает связь между поверхностным интегралом по замкнутой поверхности и тройным интегралом по пространственной области, ограниченной этой поверхностью. Эта формула является аналогом формулы Грина, которая, как известно, связывает криволинейный интеграл по замкнутой кривой с двойным интегралом по плоской области, ограниченной этой кривой. Формула Остроградского имеет широкое применение как в самом анализе, так и в его приложениях.
Выведем эту формулу для замкнутой пространственной области, граница которой пересекается с любой прямой, параллельной осям координат, не более чем в двух точках. Назовем для краткости такие области простыми. При этом будем рассматривать внешнюю сторону поверхности, ограничивающей эту область. Предполагается, что поверхность гладкая или кусочно-гладкая.
Теорема:
Пусть V — простая замкнутая область, ограниченная поверхностью S и пусть функции Р (х, у, z), Q (х, у, z) и R (х, у, z) непрерывны вместе со своими частными производными первого порядка в данной области. Тогда имеет место следующая формула: 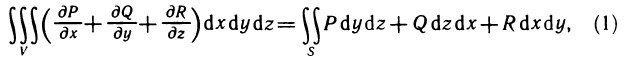 называемая формулой Остроградского.
называемая формулой Остроградского.
Доказательство:
Пусть область G — проекция поверхности S (и области V) на плоскость Оху (рис. 211), a 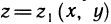 и
и 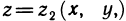 — уравнения соответствующих частей поверхности S — нижней части
— уравнения соответствующих частей поверхности S — нижней части 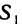 и верхней
и верхней 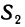 .
.
Преобразуем тройной интеграл 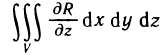
в поверхностный. Для этого сведем его к повторному интегралу и по формуле Ньютона—Лейбница выполним интегрирование по z. Получим 
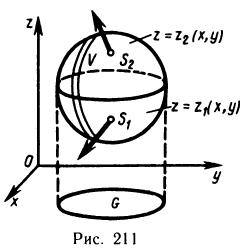
Так как область G является проекцией на плоскость Оху и поверхности  , и поверхности
, и поверхности  , то двойные интегралы можно заменить равными им поверхностными интегралами [см. § 11, п. 4, формулу (8)], взятыми соответственно по верхней стороне поверхности
, то двойные интегралы можно заменить равными им поверхностными интегралами [см. § 11, п. 4, формулу (8)], взятыми соответственно по верхней стороне поверхности  и верхней стороне поверхности
и верхней стороне поверхности 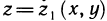 , т. е.
, т. е. 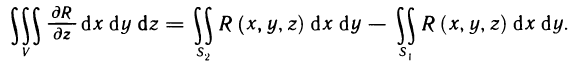
Меняя в интеграле по 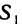 сторону поверхности, получаем
сторону поверхности, получаем 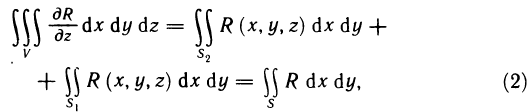
где S — внешняя сторона поверхности, ограничивающей область V.
Аналогично доказываются формулы
Складывая почленно равенства (2), (3), (4), приходим к формуле (1). ■
Замечание:
Формула Остроградского верна для любой замкнутой пространственной области V, которую можно разбить на конечное число простых областей. В самом деле, применяя формулу (1) к каждой из областей разбиения и складывая результаты, получаем в левой части равенства тройной интеграл по всей области V, а в правой — поверхностный интеграл по поверхности S, ограничивающей область V, так как поверхностные интегралы по вспомогательным поверхностям берутся дважды по противоположным сторонам и при суммировании взаимно уничтожаются.
С помощью формулы Остроградского удобно вычислять поверхностные интегралы по замкнутым поверхностям.
Пример:
Вычислить интеграл 
где S — внешняя сторона пирамиды, ограниченной плоскостями  (см. рис. 196).
(см. рис. 196).
Решение:
Используя формулу Остроградского, получаем 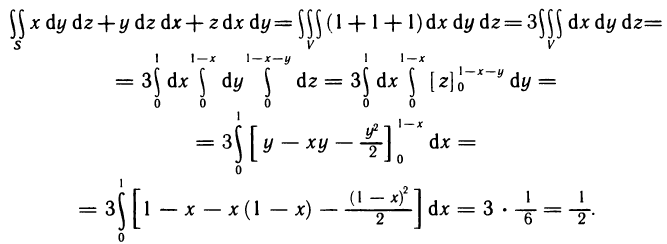
Пример:
Вычислить интеграл 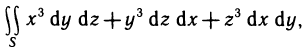
где S — внешняя сторона сферы 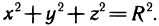
Решение:
Применяя формулу Остроградского, имеем 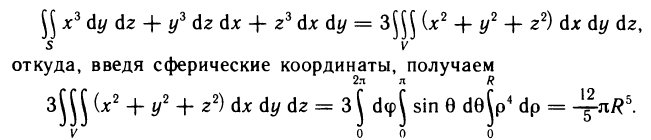
Как было отмечено (§ 9, п. 1), формула Грина выражает площадь области через криволинейный интеграл по ее границе. Точно также из формулы Остроградского легко получить выражение для объема области в виде поверхностного интеграла по замкнутой поверхности S — границе этой области. Действительно, подберем функции Р, Q и R так, чтобы 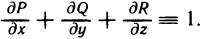
Тогда получим 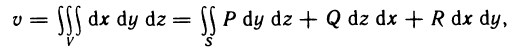
где 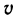 — объем, ограниченный поверхностью S. В частности, полагая
— объем, ограниченный поверхностью S. В частности, полагая 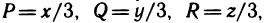 получаем для вычисления объема формулу
получаем для вычисления объема формулу 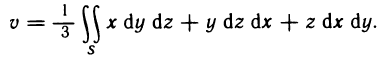
Формула Стокса
Формула Стокса устанавливает связь между поверхностным и криволинейным интегралами. Подобно формулам Грина и Остроградского, формулу Стокса широко применяют как в самом анализе, так и в его приложениях.
Пусть S — поверхность, заданная уравнением z=z(х, у), где функции  непрерывны в замкнутой области G — проекций S на плоскость Оху; L — контур, ограничивающий S, а l — его проекция на плоскость Оху, являющаяся контуром, ограничивающим область G. Выберем верхнюю сторону поверхности S (рис. 212). Тогда при сделанных предположениях справедлива следующая теорема.
непрерывны в замкнутой области G — проекций S на плоскость Оху; L — контур, ограничивающий S, а l — его проекция на плоскость Оху, являющаяся контуром, ограничивающим область G. Выберем верхнюю сторону поверхности S (рис. 212). Тогда при сделанных предположениях справедлива следующая теорема.
Теорема:
Если функция Р (х, у, z) непрерывна вместе со своими частными производными первого порядка на поверхности S, то имеет место следующая формула: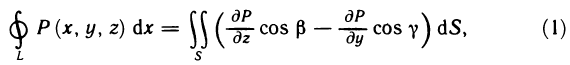
где 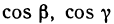 — направляющие косинусы нормали к поверхности S, а контур L пробегается в положительном направлении.
— направляющие косинусы нормали к поверхности S, а контур L пробегается в положительном направлении.
Доказательство:
Преобразуем криволинейный интеграл 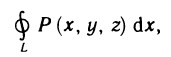
взятый по контуру L, в интеграл по поверхности S. Это преобразование проведем по следующей схеме: 
т. е. криволинейный интеграл по пространственному контуру L преобразуем сначала в криволинейный интеграл по плоскому контуру l, затем переведем его в двойной интеграл по области G и, наконец, этот последний интеграл преобразуем в интеграл по поверхности S.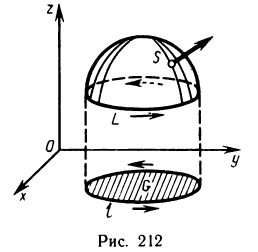
Так как контур L лежит на поверхности S, то координаты его точек удовлетворяют уравнению z=z(x, у) и поэтому значения функции Р (х, y, z) в точках контура L равны значениям функции Р [х, у, z(x, у)] в соответствующих точках контура l, являющегося проекцией L. Проекции же соответствующих участков разбиения контуров L и l на ось Ох совпадают. Поэтому совпадают также интегральные суммы для криволинейных интегралов второго рода от функции Р по контурам L и l, а значит, равны и интегралы: 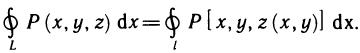
Далее, применяя формулу Грина, перейдем к двойному интегралу по области G. Получаем 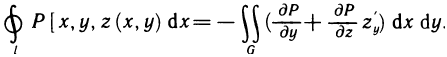
Здесь подынтегральная функция равна частной производной по у от сложной функции, получающейся из Р (х, у, z) после подстановки
z (x, у) вместо z.
Поскольку s — верхняя сторона поверхности, т. е. 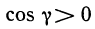 (
( — острый угол между нормалью и осью Oz), нормаль имеет проекции —
— острый угол между нормалью и осью Oz), нормаль имеет проекции — 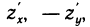 1. А так как направляющие косинусы нормали пропорциональны соответствующим проекциям, то
1. А так как направляющие косинусы нормали пропорциональны соответствующим проекциям, то 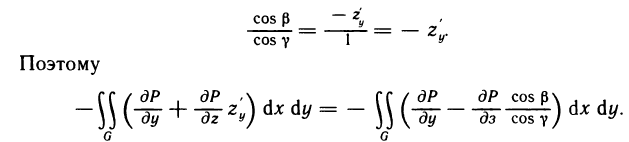
Теперь, воспользовавшись формулами (8) и (11) из § 11, можно этот двойной интеграл преобразовать в поверхностный. Получаем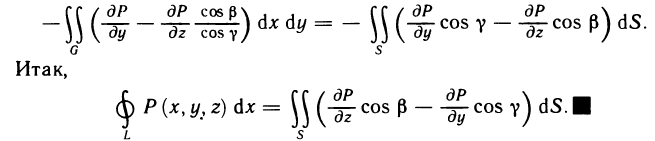
Аналогично доказывается при соответствующих условиях справедливость следующих двух формул: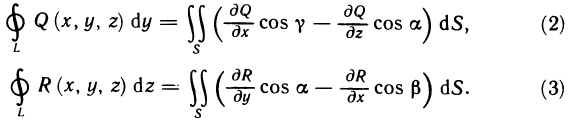
Складывая почленно равенства (1), (2), (3), получаем формулу 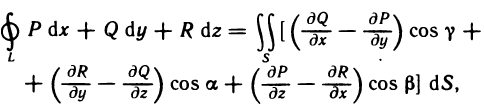
которая называется формулой Стокса.
С помощью формулы, связывающей поверхностные интегралы, (14) из § 11 формулу Стокса можно переписать в следующем виде: 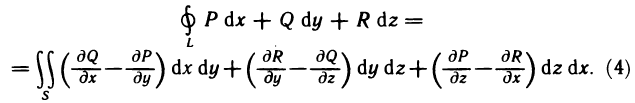
Формулу Стокса легко запомнить, заметив, что первое слагаемое в правой ее части это то же самое выражение, которое стоит под знаком двойного интеграла в формуле Грина, а второе и третье получаются из него циклической перестановкой координат х, у, z и функций Р, Q, R.
В частности, если поверхность S — область плоскости Оху, ограниченная контуром L, то интегралы по dzdx и dydz обращаются в нуль и формула Стокса переходит в формулу Грина.
Формула Стокса позволяет вычислять криволинейные интегралы по замкнутым контурам с помощью поверхностных интегралов.
Пример:
Вычислить с помощью формулы Стокса интеграл 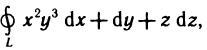
где L — окружность, заданная уравнениями  а поверхностью S служит верхняя сторона полусферы
а поверхностью S служит верхняя сторона полусферы  и контур L проходится в положительном направлении.
и контур L проходится в положительном направлении.
Решение:
Так как  то криволинейный интеграл по любой пространственной замкнутой кривой L равен нулю:
то криволинейный интеграл по любой пространственной замкнутой кривой L равен нулю: 
А это значит, что в данном случае криволинейный интеграл не зависит от выбора пути интегрирования.
Как и в случае плоской кривой, условия (5) являются необходимыми и достаточными для выполнения равенства (6).
При выполнении условий (5) или (6) подынтегральное выражение 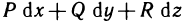 представляет собой полный дифференциал некоторой функции U (х, у, z):
представляет собой полный дифференциал некоторой функции U (х, у, z): 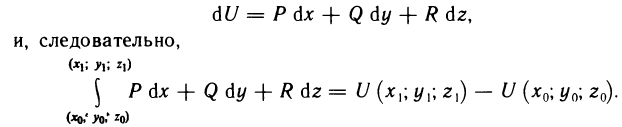
Справедливость этого равенства устанавливается так же, как соответствующая формула (4) из § 8 для функции двух переменных.
Скалярное и векторное поля
Понятие поля лежит в основе многих представлений современной физики. Изучение теории поля выходит за рамки данного курса, поэтому ограничимся только краткими сведениями.
В общем случае говорят, что в пространстве задано поле некоторой величины u, если в каждой точке пространства (или некоторой его части) определено значение этой величины. Так, например, при изучении потока газа приходится исследовать несколько полей: температурное поле (в каждой точке температура имеет определенное значение), поле давлений, поле скоростей и т. д.
Поле величины u называется стационарным (или установившимся), если и не зависит от времени t. В противном случае поле называется нестационарным (или неустановившимся). Таким образом, величина u есть функция точки М и времени t.
В физических задачах чаще всего приходится иметь дело со скалярными и векторными величинами. В соответствии с этим различают два вида полей: скалярные и векторные. Для простоты будем считать их стационарными.
Скалярное поле
Пусть G — некоторая область на плоскости или в пространстве. Если в каждой точке М из G определена скалярная величина u, то говорят, что в области G задано скалярное поле. Понятия скалярного поля и функции, определенной в области G, совпадают. Обычно используют следующую терминологию: скалярное поле задается с помощью функции u=F(M), которая называется скалярной функцией. Если в пространстве ввести систему координат Oxyz, то каждая точка М будет иметь определенные координаты х, у, z и скалярная величина и является функцией этих координат: u=F(М)= F(х, у, z).
Примером скалярного поля может служить поле температур воздуха в некотором помещении, если температуру рассматривать как функцию точки. В точках, расположенных ближе к источнику теплоты, температура выше, дальше от источника теплоты — ниже.
Если окажется, что температура везде одинаковая, то в этом случае скалярное поле постоянно.
Векторное поле
Аналогично с понятием скалярного поля вводится понятие векторного поля: если в каждой точке М из G определен вектор  (М), то говорят, что в области G задано векторное поле. Функция
(М), то говорят, что в области G задано векторное поле. Функция  (M), с помощью которой задается векторное поле, называется векторной функцией.
(M), с помощью которой задается векторное поле, называется векторной функцией.
Примером векторного поля может служить поле сил любой природы. Каждой точке области соответствует определенный вектор, имеющий числовую величину и направление силы в этой точке.
Пример:
Найти векторное поле скоростей 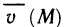 точек твердого тела, вращающегося с постоянной угловой скоростью
точек твердого тела, вращающегося с постоянной угловой скоростью 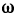 вокруг оси.
вокруг оси.
Решение:
Скорость 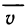 точки М равна векторному произведению
точки М равна векторному произведению 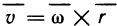 где
где 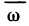 — вектор угловой скорости;
— вектор угловой скорости; 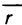 — радиус-вектор точки М вращающегося тела относительно какой-либо точки оси вращения. Примем эту неподвижную точку оси за начало координат, а ось вращения — за ось Oz. Тогда
— радиус-вектор точки М вращающегося тела относительно какой-либо точки оси вращения. Примем эту неподвижную точку оси за начало координат, а ось вращения — за ось Oz. Тогда 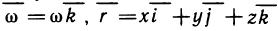 и, следовательно.
и, следовательно.
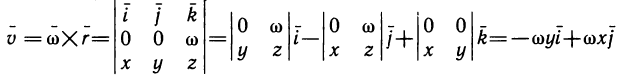
— искомое векторное поле.
Потенциальное поле
Введем понятие потенциального поля. Рассмотрим некоторое скалярное поле F(М). Если в каждой точке М из G определен вектор grad F, то поле этого вектора называется потенциальным полем. Само скалярное поле называется при этом потенциалом векторного поля, а вектор, определяющий потенциальное поле, часто называют потенциальным вектором, т. е. вектор 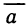 (М) потенциальный, если найдется такая скалярная функция F(M), что
(М) потенциальный, если найдется такая скалярная функция F(M), что 
Возникает вопрос, при каких условиях данное векторное поле  (М) потенциальное. Фактически этот вопрос уже рассмотрен в § 7. Пусть Р, Q и R — проекции вектора
(М) потенциальное. Фактически этот вопрос уже рассмотрен в § 7. Пусть Р, Q и R — проекции вектора 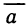 на оси координат Ox, Оу, Oz соответственно, т. е.
на оси координат Ox, Оу, Oz соответственно, т. е. 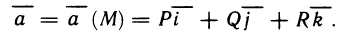
В силу соотношения (1) векторное поле 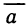 (М) является потенциальным, если найдется функция F (М) такая, что
(М) является потенциальным, если найдется функция F (М) такая, что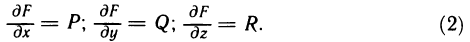
В теореме 13.7 было показано, что выражение 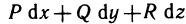 (где P, Q, R — непрерывные функции, имеющие непрерывные частные производные первого порядка) полный дифференциал некоторой функции F (х, у, z) в том и только в том случае, когда Р, Q, R удовлетворяют условиям
(где P, Q, R — непрерывные функции, имеющие непрерывные частные производные первого порядка) полный дифференциал некоторой функции F (х, у, z) в том и только в том случае, когда Р, Q, R удовлетворяют условиям 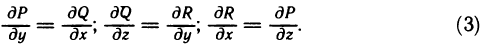
Но если 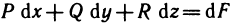 , то справедливы и равенства (2),
, то справедливы и равенства (2),
т. е. условие (3) как раз и означает, что данное векторное поле потенциальное. Функция F (х, у, z) в этом случае называется потенциальной функцией поля.
Примером потенциального поля служит поле сил тяготения. Если в начале координат помещена масса т, то эта масса создает поле сил тяготения; в каждой точке М пространства на помещенную в эту точку единичную массу по закону Ньютона действует сила  (М), равная по величине
(М), равная по величине 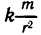 и направленная к началу координат. Здесь
и направленная к началу координат. Здесь 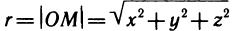 — расстояние от начала координат О до точки М; k — коэффициент пропорциональности.
— расстояние от начала координат О до точки М; k — коэффициент пропорциональности.
Пусть х, у, z — координаты точки М. Тогда проекции Р, Q и R силы 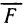 (М) определяются следующим образом:
(М) определяются следующим образом: 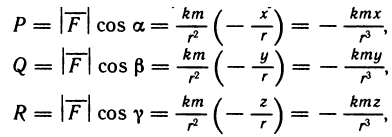
где 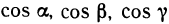 — направляющие косинусы вектора
— направляющие косинусы вектора 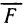 (М). Следовательно,
(М). Следовательно,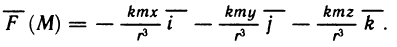
Можно проверить, что данное векторное поле потенциальное и его потенциальная функция 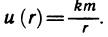
В заключение найдем работу силы 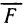 (М) при перемещении единичной массы из точки
(М) при перемещении единичной массы из точки 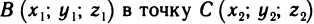 .
.
Как известно, работа А выражается криволинейным интегралом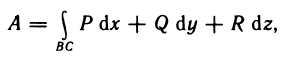
где Р, Q и R — проекции силы  (М) на оси координат. Так как данное силовое поле является потенциальным, то подынтегральное выражение представляет собой полный дифференциал, поэтому интеграл не зависит от выбора пути интегрирования и может быть вычислен по формуле
(М) на оси координат. Так как данное силовое поле является потенциальным, то подынтегральное выражение представляет собой полный дифференциал, поэтому интеграл не зависит от выбора пути интегрирования и может быть вычислен по формуле 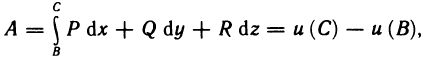
т. е. работа силы 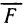 (М) равна разности значений потенциальной функции в точках С и В. В данном случае
(М) равна разности значений потенциальной функции в точках С и В. В данном случае 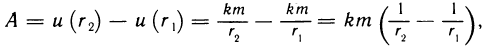
где  — расстояния точек B и С от начала координат.
— расстояния точек B и С от начала координат.
Заметим, что областью, в которой определено поле сил тяготения, является все пространство, за исключением начала координат.
Задача о потоке векторного поля
Пусть в пространстве задано векторное поле  скоростей жидкости, т. е. пространство заполнено движущейся жидкостью, скорость которой в каждой точке М (х; у, z) задается вектором
скоростей жидкости, т. е. пространство заполнено движущейся жидкостью, скорость которой в каждой точке М (х; у, z) задается вектором 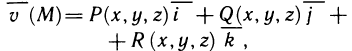
где Р, Q и R — проекции скорости на оси координат. Пусть Р, Q и R — непрерывные функции координат. Вычислим количество П жидкости, протекающей за единицу времени через некоторую ориентированную поверхность S, ограниченную пространственной кривой L, считая плотность жидкости 
Пусть 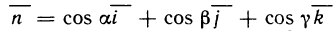 — единичный вектор нормали к поверхности S, и пусть его направляющие косинусы являются непрерывными функциями координат х, у, z точек данной поверхности.
— единичный вектор нормали к поверхности S, и пусть его направляющие косинусы являются непрерывными функциями координат х, у, z точек данной поверхности.
Разобьем поверхность S произвольно на n частей с площадями  и в каждой из них выберем точку
и в каждой из них выберем точку 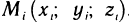
Найдем количество П, жидкости, протекающей за единицу времени через i-ю часть поверхности (рис. 213). Обозначим через  угол между векторами
угол между векторами 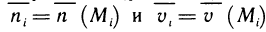 . Если этот угол острый, т. е. жидкость течет в «ту сторону», куда указывает нормаль
. Если этот угол острый, т. е. жидкость течет в «ту сторону», куда указывает нормаль 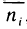 , то величину
, то величину 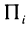 будем считать положительной, а если угол тупой, т. е. жидкость течет в «обратную сторону», — отрицательной.
будем считать положительной, а если угол тупой, т. е. жидкость течет в «обратную сторону», — отрицательной.
Приближенно можно считать, что при достаточно мелком разбиении поверхности S скорость 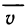 во всех точках i-й части постоянна и равна
во всех точках i-й части постоянна и равна 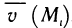 , а частичные поверхности — плоские. Тогда величина
, а частичные поверхности — плоские. Тогда величина  приближенно равна взятому с соответствующим знаком объему цилиндра с площадью основания
приближенно равна взятому с соответствующим знаком объему цилиндра с площадью основания 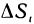 и высотой, равной модулю проекции вектора
и высотой, равной модулю проекции вектора 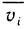 на нормаль
на нормаль 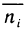 , т. е.
, т. е. 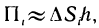 где h — указанная проекция. А так как
где h — указанная проекция. А так как 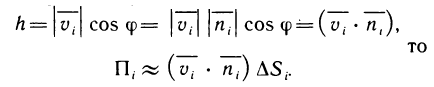
Суммируя по i от l до n, получаем приближенное значение количества П жидкости, протекающей через ориентированную поверхность S за единицу времени: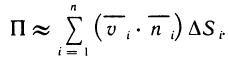
Сумма справа является интегральной суммой для функции 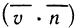 . Так как проекции Р, Q, R вектора
. Так как проекции Р, Q, R вектора 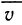 и направляющие косинусы вектора
и направляющие косинусы вектора 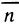 — непрерывные функции координат х, у, z точек поверхности S, то скалярное произведение
— непрерывные функции координат х, у, z точек поверхности S, то скалярное произведение 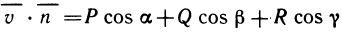 непрерывная функция. Следовательно, предел этой суммы при стремлении к нулю наибольшего из диаметров частей поверхности существует и равен поверхностному интегралу первого рода по поверхности S от функции
непрерывная функция. Следовательно, предел этой суммы при стремлении к нулю наибольшего из диаметров частей поверхности существует и равен поверхностному интегралу первого рода по поверхности S от функции  . Переходя к пределу, получаем точное значение П:
. Переходя к пределу, получаем точное значение П:

или, выражая скалярное произведение через координаты векторов,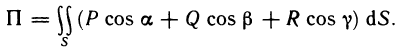
Воспользовавшись формулой (14) из § 11, связывающей поверхностные интегралы первого и второго рода, окончательно имеем 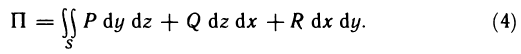
Таким образом, количество П жидкости, протекающей за единицу времени через ориентированную поверхность S, представляет собой поверхностный интеграл второго рода по выбранной стороне поверхности.
Для произвольного векторного поля  поверхностный интеграл второго рода (4) называется потоком вектора
поверхностный интеграл второго рода (4) называется потоком вектора  [или потоком векторного поля
[или потоком векторного поля  ] через поверхность S. Для векторного поля иной природы, чем в рассмотренном примере, поток, разумеется, имеет другой физический смысл.
] через поверхность S. Для векторного поля иной природы, чем в рассмотренном примере, поток, разумеется, имеет другой физический смысл.
Дивергенция
Пусть в некоторой области V, ограниченной поверхностью S, задано векторное поле 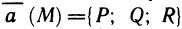 , такое, что функции P(M), Q (М), R (М) непрерывны в V вместе с частными производными.
, такое, что функции P(M), Q (М), R (М) непрерывны в V вместе с частными производными.
Определение:
Дивергенцией векторного поля 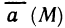 называется скалярная функция
называется скалярная функция 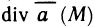 , определяемая равенством
, определяемая равенством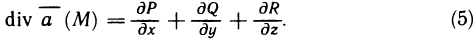
Используя выражение для дивергенции и понятие потока вектора через поверхность, формулу Остроградского (см. формулу (1), § 12) можно записать в более компактной векторной форме. Поверхностный интеграл в формуле Остроградского представляет собой поток вектора 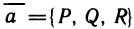 через поверхность S:
через поверхность S: 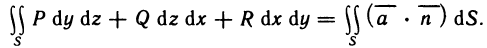
Используя это выражение и формулу (5), запишем формулу Остроградского в виде 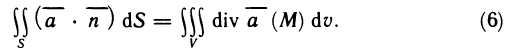
Таким образом, поток вектора 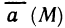 через замкнутую поверхность S равен тройному интегралу от дивергенции поля
через замкнутую поверхность S равен тройному интегралу от дивергенции поля  , взятому по области, ограниченной поверхностью S.
, взятому по области, ограниченной поверхностью S.
Покажем, что дивергенция не зависит от выбора системы координат, хотя ее определение и было с ней связано. Для этого возьмем произвольную точку Л1, заключим ее в область V, ограниченную поверхностью S, и применим к области V формулу Остроградскаго. Далее, используя теорему о среднем для тройного интеграла, получаем 
где  —некоторая точка области V;
—некоторая точка области V; 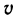 — объем области V. Отсюда
— объем области V. Отсюда 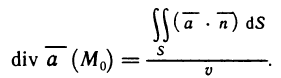
Будем теперь стягивать область V в точку М. При этом 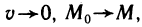 и мы получаем
и мы получаем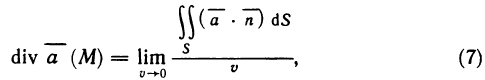
т. е. дивергенция векторного поля 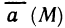 в точке М является пределом отношения потока вектора
в точке М является пределом отношения потока вектора 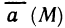 через поверхность S, окружающую точку М, к объему области. А так как поток и объем не зависят от выбора системы координат, то и дивергенция также не зависит от выбора системы координат, что и требовалось показать.
через поверхность S, окружающую точку М, к объему области. А так как поток и объем не зависят от выбора системы координат, то и дивергенция также не зависит от выбора системы координат, что и требовалось показать.
Выясним теперь с помощью формулы (7) физический смысл дивергенции. Для этого будем рассматривать векторное поле 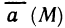 как поле скоростей жидкости с плотностью р=1. Как установлено в п. 4, поток
как поле скоростей жидкости с плотностью р=1. Как установлено в п. 4, поток
вектора 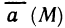 равен количеству жидкости, протекающей за единицу времени через поверхность S в направлении нормали
равен количеству жидкости, протекающей за единицу времени через поверхность S в направлении нормали 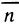 . Пусть
. Пусть 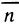 — внешняя нормаль. Поскольку S — замкнутая поверхность, то, очевидно, поток вектора
— внешняя нормаль. Поскольку S — замкнутая поверхность, то, очевидно, поток вектора 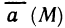 равен количеству жидкости, которое за единицу времени возникает или уничтожается в пределах области V, ограниченной поверхностью S. Назовем это количество суммарной мощностью источников (если П>0) или стоков (если П<0), расположенных в области V. Рассмотрим отношение
равен количеству жидкости, которое за единицу времени возникает или уничтожается в пределах области V, ограниченной поверхностью S. Назовем это количество суммарной мощностью источников (если П>0) или стоков (если П<0), расположенных в области V. Рассмотрим отношение 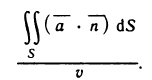
Оно представляет собой среднюю плотность источников (или стоков), т. е. количество жидкости, возникающей (или исчезающей) за единицу времени в единице объема области V, а предел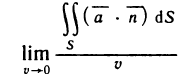
при условии, что область V стягивается в точку М, можно назвать плотностью источников (или стоков) в точке М. Но этот предел равен 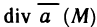 . Таким образом, дивергенция векторного поля скоростей характеризует плотность источников жидкости.
. Таким образом, дивергенция векторного поля скоростей характеризует плотность источников жидкости.
Если 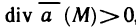 , то, как следует из формулы (6), П>0, т. е. внутри области V имеются источники жидкости и из нее вытекает жидкости больше, чем втекает; если
, то, как следует из формулы (6), П>0, т. е. внутри области V имеются источники жидкости и из нее вытекает жидкости больше, чем втекает; если 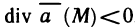 , то П<0, т. е. внутри области V имеются стоки жидкости и в нее втекает жидкости больше, чем вытекает. Если же
, то П<0, т. е. внутри области V имеются стоки жидкости и в нее втекает жидкости больше, чем вытекает. Если же 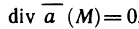 , то П=0, т. е. внутри области V нет ни стоков, ни источников и в нее втекает столько же жидкости, сколько и вытекает. Это, например, имеет место для любой области V, расположенной в потоке воды, текущей в реке.
, то П=0, т. е. внутри области V нет ни стоков, ни источников и в нее втекает столько же жидкости, сколько и вытекает. Это, например, имеет место для любой области V, расположенной в потоке воды, текущей в реке.
Для произвольного векторного поля 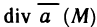 имеет аналогичный физический смысл: дивергенция характеризует плотность источников поля.
имеет аналогичный физический смысл: дивергенция характеризует плотность источников поля.
Векторное поле 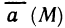 называется соленоидальным (или трубчатым), если в каждой его точке
называется соленоидальным (или трубчатым), если в каждой его точке 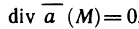 . Примером такого поля служит, как было показано выше, поле скоростей жидкости при отсутствии стоков и источников.
. Примером такого поля служит, как было показано выше, поле скоростей жидкости при отсутствии стоков и источников.
Пример:
Вычислить дивергенцию поля скоростей 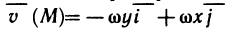 твердого тела, вращающегося с постоянной угловой скоростью ш вокруг оси Oz.
твердого тела, вращающегося с постоянной угловой скоростью ш вокруг оси Oz.
Решение. Здесь 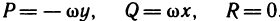 . Поэтому
. Поэтому 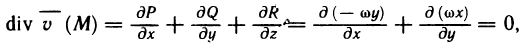 т. е. данное векторное поле является соленоидальным.
т. е. данное векторное поле является соленоидальным.
Циркуляция. Ротор
Пусть снова в некоторой области задано векторное поле 
и L — гладкая или кусочно-гладкая кривая, расположенная в этой области. Выберем на кривой L одно из двух направлений движения и обозначим через 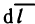 вектор, имеющий в каждой точке направление, совпадающее с направлением движения по кривой в этой точке, и по модулю равный дифференциалу длины дуги:
вектор, имеющий в каждой точке направление, совпадающее с направлением движения по кривой в этой точке, и по модулю равный дифференциалу длины дуги: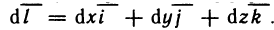
Тогда криволинейный интеграл от скалярного произведения векторов 

называется циркуляцией векторного поля  вдоль кривой L. В силовом поле циркуляция выражает работу силового поля при перемещении материальной точки вдоль пути L. Для полей другой природы циркуляция имеет иной физический смысл.
вдоль кривой L. В силовом поле циркуляция выражает работу силового поля при перемещении материальной точки вдоль пути L. Для полей другой природы циркуляция имеет иной физический смысл.
Определение:
Ротором векторного поля  называется вектор
называется вектор 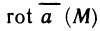 , определяемый равенством
, определяемый равенством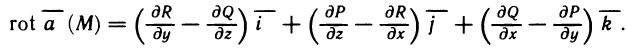 С помощью понятий ротора и циркуляции формулу Стокса
С помощью понятий ротора и циркуляции формулу Стокса 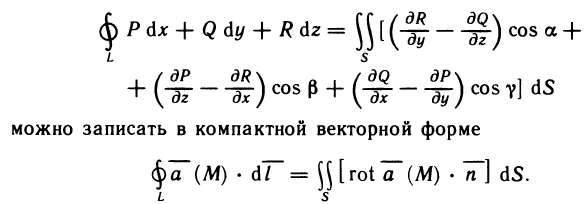
Таким образом, циркуляция векторного поля 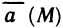 вдоль замкнутого контура L равна потоку ротора этого векторного поля через поверхность S, ограниченную контуром L.
вдоль замкнутого контура L равна потоку ротора этого векторного поля через поверхность S, ограниченную контуром L.
Так же как и для дивергенции, можно показать, что 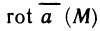 не зависит от выбора системы координат, а определяется только самим векторным полем
не зависит от выбора системы координат, а определяется только самим векторным полем 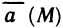 .
.
Пример:
Вычислить ротор поля скоростей 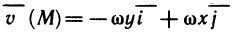 твердого тела, вращающегося с постоянной угловой скоростью
твердого тела, вращающегося с постоянной угловой скоростью  вокруг оси Oz.
вокруг оси Oz.
Решение:
Используя определение ротора, получаем 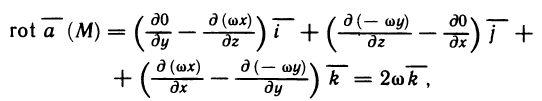
т. е. ротор данного векторного поля направлен по оси вращения Oz, а по модулю равен удвоенной угловой скорости.
Понятие ротора непосредственно связано с понятием потенциального поля. Было показано, что векторное поле 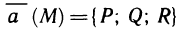 потенциальное в том и только в том случае, если
потенциальное в том и только в том случае, если 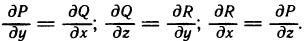
Но это означает, равенство нулю всех трех координат ротора поля  , т. е. для того чтобы векторное поле
, т. е. для того чтобы векторное поле 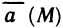 было потенциальным, необходимо и достаточно, чтобы выполнялось условие
было потенциальным, необходимо и достаточно, чтобы выполнялось условие 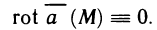
Оператор Гамильтона
Основные понятия теории поля: градиент, дивергенция, ротор и операции над ними удобно представлять с помощью оператора Гамильтона, или оператора «набла»: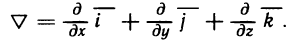
Оператор  будем рассматривать как символический вектор с координатами
будем рассматривать как символический вектор с координатами  , а операции с ним проводить по правилам векторной алгебры. При этом под произведением ,
, а операции с ним проводить по правилам векторной алгебры. При этом под произведением , 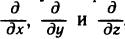 на скалярную функцию будем понимать частную производную этой функции соответственно по х, у и z.
на скалярную функцию будем понимать частную производную этой функции соответственно по х, у и z.
Основные понятия теории поля: градиент, дивергенция, ротор и операции над ними удобно представлять с помощью оператора Гамильтона, или оператора «набла»: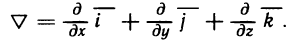
Оператор  будем рассматривать как символический вектор с координатами
будем рассматривать как символический вектор с координатами 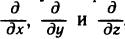 , а операции с ним проводить по правилам векторной алгебры. При этом под произведением ,
, а операции с ним проводить по правилам векторной алгебры. При этом под произведением , 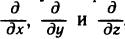 на скалярную функцию будем понимать частную производную этой функции соответственно по х, у и z.
на скалярную функцию будем понимать частную производную этой функции соответственно по х, у и z.
Примеры:
1. Пусть u (x, у, z) — скалярная функция. Тогда произведение оператора  на функцию u дает градиент этой функции:
на функцию u дает градиент этой функции:
2. Пусть 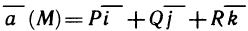 — вектор-функция. Тогда скалярное произведение оператора
— вектор-функция. Тогда скалярное произведение оператора  на вектор-функцию
на вектор-функцию 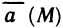 дает дивергенцию этой функции
дает дивергенцию этой функции 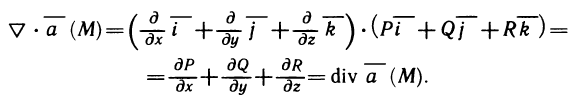
3. Векторное произведение оператора  на вектор-функцию
на вектор-функцию 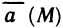 дает ротор этой функции
дает ротор этой функции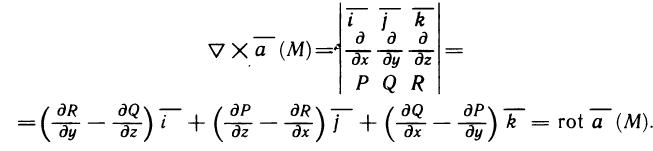
В приложениях часто встречаются так называемые операции второго порядка, т. е. попарные комбинации трех указанных выше операций. Рассмотрим наиболее важные из них. 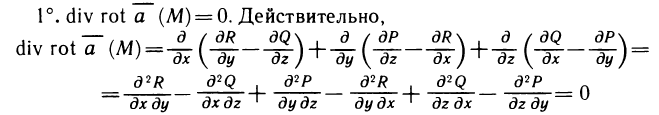
в силу равенства смешанных производных второго порядка. Этот же результат легко получить с помощью оператора  :
:
так как здесь имеем смешанное произведение трех «векторов»: 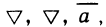 два из которых одинаковы. Такое произведение, очевидно, равно нулю.
два из которых одинаковы. Такое произведение, очевидно, равно нулю.
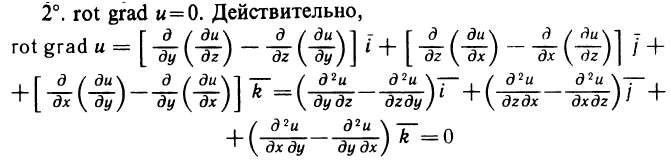 в силу равенства смешанных производных второго порядка. Этот же результат легко получить с помощью оператора
в силу равенства смешанных производных второго порядка. Этот же результат легко получить с помощью оператора  :
: 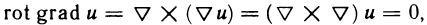
так как векторное произведение одинаковых «векторов» равно нулю.
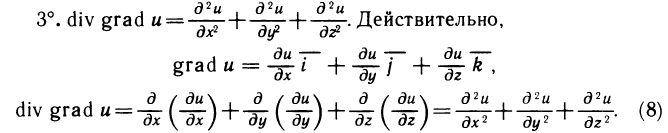
Правая часть равенства (8) символически обозначается так: 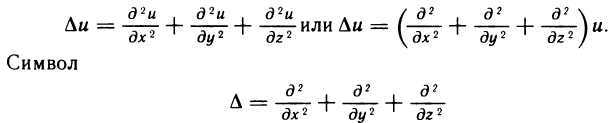
называется оператором Лапласа*. Оператор Лапласа  естественно рассматривать как скалярный квадрат «вектора»
естественно рассматривать как скалярный квадрат «вектора»  . В самом деле,
. В самом деле, 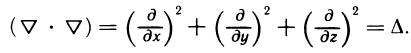
Поэтому равенство (8) с помощью оператора  записывается в виде
записывается в виде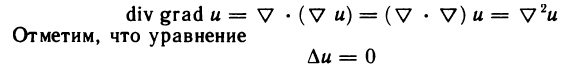
называется уравнением Лапласа. С его помощью описываются стационарные процессы различной физической природы, например: стационарное распределение теплоты, электростатическое поле точечных зарядов, установившееся движение несжимаемой жидкости внутри некоторой области и т. д. Скалярное поле u (х, у, z), удовлетворяющее условию 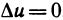 , называется лапласовым, или гармоническим, полем.
, называется лапласовым, или гармоническим, полем.
Дополнение к интегрированию



Смотрите также:
| Максимумы и минимумы | Задача практического интегрирования |
| Теорема о среднем | Многочлены |
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

