а) Тригонометрический предел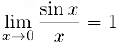 
.
Найдем двустороннюю оценку для функции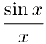 
. воспользовавшись геометрическими соображениями.
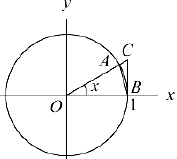
Прежде всего заметим, что ввиду четности данной функции мы можем ограничиться лишь малыми положительными значениями х. Обозначим через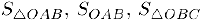 
площади треугольника ОАВ, сектора ОАВ и треугольника ОВС. Так как
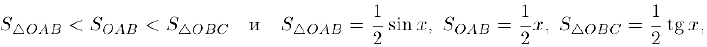
то справедливо неравенство:
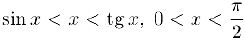
откуда
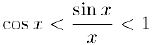
Покажем, что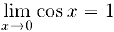 
. Действительно, из неравенства (1) следует, что
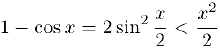
поэтому, для любого положительного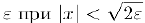 
выполняется неравенство 
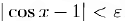, а это и означает, что 
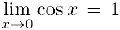. Возвращаясь теперь к неравенству (2). замечаем, что к функциям, входящим в него применимо свойство 4) предела функции, и, стало быть,
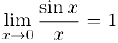
Из тригонометрического предела следует, что
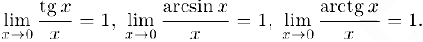
В самом деле.
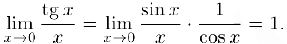
Далее, из неравенства (1) мы заключаем, что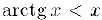 
, откуда 
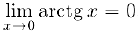, а, значит, и 
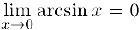. так как 
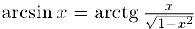. Следовательно, воспользовавшись свойством 2) предела композиции функции и тригонометрическим пределом, получим:
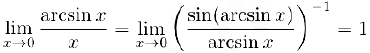
Аналогично доказывается последнее из утверждений (3).
Замечание. Как следует из свойства 2) предела композиции функций, во всех приведенных тригонометрических пределах вместо аргумента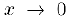 
мы можем использовать функцию 
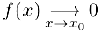. Таким образом,
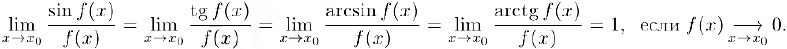
Эта лекция взята со страницы онлайн помощи по математическому анализу:
Математический анализ онлайн помощь
Возможно эти страницы вам будут полезны:
