Оглавление:
Страница содержит справочный материал по курсу «Дифференциальное исчисление функций одной переменной», подробно разобраны методы решения типовых задач.
Определение производной
1°. Производная непрерывной функции 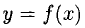 в точке
в точке 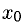 определяется по следующему алгоритму.
определяется по следующему алгоритму.
1) Вычислить 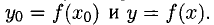
2) Составить приращение функции  соответствующее приращению аргумента
соответствующее приращению аргумента 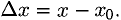
3) Составить отношение приращений 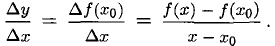
4) Найти предел 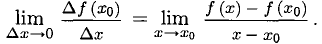
Если предел существует и конечен, то он обозначается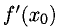 и называется производной функции
и называется производной функции 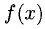 в точке
в точке 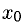 , а функция
, а функция 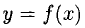 называется дифференцируемой в точке
называется дифференцируемой в точке 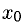 .
.
2°. Если вместо фиксированной точки хо взять переменную величину х, то производная
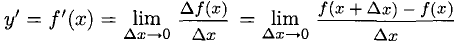
будет функцией от х.
Число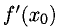 можно получить также подстановкой
можно получить также подстановкой 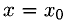 в выражение для
в выражение для 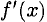 ; это обозначается так:
; это обозначается так: 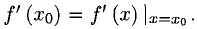
Например, если у = С (С — константа), то 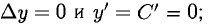
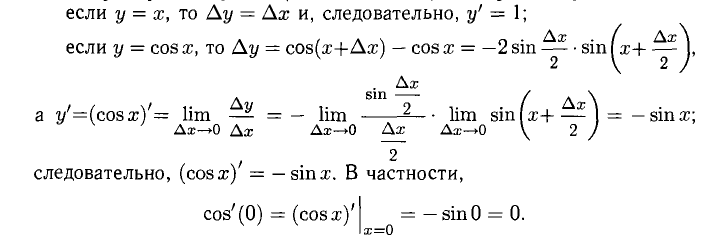
Геометрическая, механическая и экономическая интерпретации производной
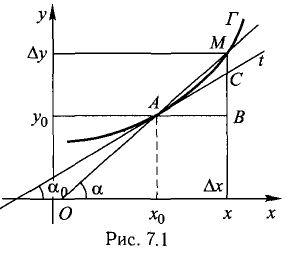
1°. Выясним геометрический смысл отдельных пунктов определения производной, исходя из рис. 7.1, где изображен график Г возрастающей функции, а 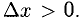 Имеем:
Имеем: 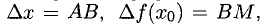
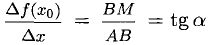 — угловой коэффициент секущей AM, проведенной через фиксированную точку
— угловой коэффициент секущей AM, проведенной через фиксированную точку 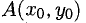 и переменную точку
и переменную точку 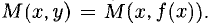 При
При 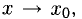 или
или 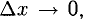 точка М(х,у) приближается к А вдоль Г, а секущая AM превращается в касательную t с угловым коэффициентом
точка М(х,у) приближается к А вдоль Г, а секущая AM превращается в касательную t с угловым коэффициентом 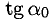 (рис. 7.1):
(рис. 7.1):
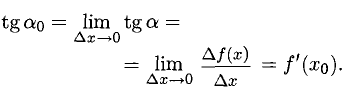
Вывод. Существование производной 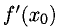 равносильно существованию касательной t к Г в точке
равносильно существованию касательной t к Г в точке 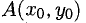 , и
, и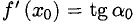 есть ее угловой коэффициент. Уравнение касательной t имеет вид
есть ее угловой коэффициент. Уравнение касательной t имеет вид
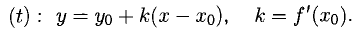
2°. Прямая, перпендикулярная касательной в точке касания 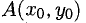 , называется нормалью к кривой Г. Уравнение нормали п имеет вид
, называется нормалью к кривой Г. Уравнение нормали п имеет вид
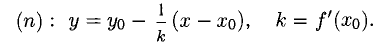
3°. Если S = S(t) — путь, пройденный материальной точкой М за время t, то 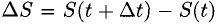 — путь, пройденный М за время
— путь, пройденный М за время 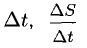 — средняя скорость движения за время
— средняя скорость движения за время 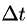 , а производная
, а производная
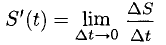
— мгновенная скорость точки М в момент времени t.
4°. Пусть 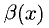 обозначает прибыль, полученную в результате вложения в некоторое производство х денежных единиц (д. ед.). Дополнительное вложение h д. ед. изменит (увеличит или уменьшит) прибыль на
обозначает прибыль, полученную в результате вложения в некоторое производство х денежных единиц (д. ед.). Дополнительное вложение h д. ед. изменит (увеличит или уменьшит) прибыль на 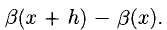 Тогда прибыль на одну д. ед. вложения равна
Тогда прибыль на одну д. ед. вложения равна 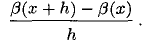 При достаточно малом h приходим к
При достаточно малом h приходим к
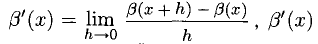
— коэффициент изменения прибыли, показывающий динамику ее изменения; 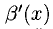 называется маргинальной прибылью, соответствующей затраченной сумме х.
называется маргинальной прибылью, соответствующей затраченной сумме х.
Примеры с решениями
Пример:
Составить уравнения касательной и нормали к параболе в 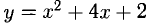 точке A(1, 7).
точке A(1, 7).
Решение:
Точка А( 1,7) лежит на параболе. Находим 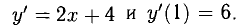 Следовательно (см. п. 1°), уравнение касательной имеет вид у = 7 + 6(х — 1), т.е. у = 6х + 1, а уравнение нормали (см. п. 2°)
Следовательно (см. п. 1°), уравнение касательной имеет вид у = 7 + 6(х — 1), т.е. у = 6х + 1, а уравнение нормали (см. п. 2°)
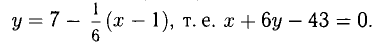
Пример:
Составить уравнение прямой, проходящей через точку В(-1,2) касательно параболе 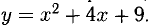
Решение:
Точка В(-1,2) не лежит на параболе, поэтому способ, приведенный выше, неприменим. Обозначим через 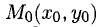 ) точку касания искомой касательной с параболой. Тогда
) точку касания искомой касательной с параболой. Тогда 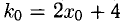 — угловой коэффициент этой прямой. Равенство
— угловой коэффициент этой прямой. Равенство 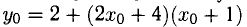 означает, что прямая, касательная к параболе, проходит через точки В(-1,2) и
означает, что прямая, касательная к параболе, проходит через точки В(-1,2) и 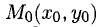 , а равенство
, а равенство 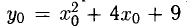 означает, что
означает, что 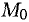 лежит на параболе. Из этих двух уравнений находим:
лежит на параболе. Из этих двух уравнений находим:
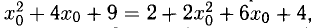
т.е 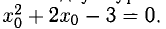 Отсюда
Отсюда 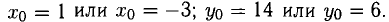 Таким образом, точками касания на параболе могут быть
Таким образом, точками касания на параболе могут быть 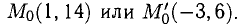 Уравнения касательных можно составить по двум парам точек
Уравнения касательных можно составить по двум парам точек 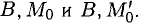 Сами уравнения имеют вид у = —2х, у = 6х + 8.
Сами уравнения имеют вид у = —2х, у = 6х + 8.
Связь дифференцируемости с непрерывностью
1°. Напомним: функция, имеющая конечную производную в данной точке, называется дифференцируемой в этой точке, в противном случае — недифференцируемой.
Теорема:
Если функция дифференцируема в данной точке, то в этой точке она непрерывна.
Из существования 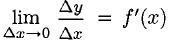 следует, что
следует, что 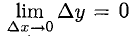 (непрерывность), так как в противном случае
(непрерывность), так как в противном случае 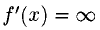 либо не существует.
либо не существует.
2°. Функция, непрерывная в данной точке, не обязательно дифференцируема в этой точке.
Например, функция 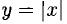 непрерывна, но не дифференцируема в точке х = 0, поскольку действия алгоритма с учетом
непрерывна, но не дифференцируема в точке х = 0, поскольку действия алгоритма с учетом 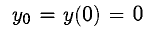 приводят к
приводят к 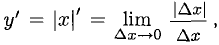 а этот предел не существует (при
а этот предел не существует (при 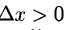 выражение под знаком предела равно 1, а при
выражение под знаком предела равно 1, а при 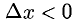 оно равно -1);
оно равно -1);
функция 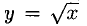 в точке х = 0 непрерывна; она определена только
в точке х = 0 непрерывна; она определена только 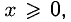 поэтому можно брать только
поэтому можно брать только 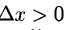 Имеем
Имеем
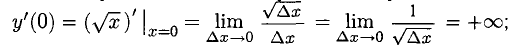
функция 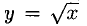 имеет в точке х = 0 бесконечную производную и потому не дифференцируема в этой точке. Касательная к графику Г перпендикулярна к оси Ох.
имеет в точке х = 0 бесконечную производную и потому не дифференцируема в этой точке. Касательная к графику Г перпендикулярна к оси Ох.
3°. Функция, дифференцируемая в каждой точке данного интервала, называется дифференцируемой в этом интервале. Функция с непрерывно изменяющейся производной (касательной) называется гладкой. График функции у = |x| не гладкий при х=0 (имеет угол).
Таблица производных и правила дифференцирования
1°. Дифференцирование основных элементарных функций осуществляется при помощи следующих формул:

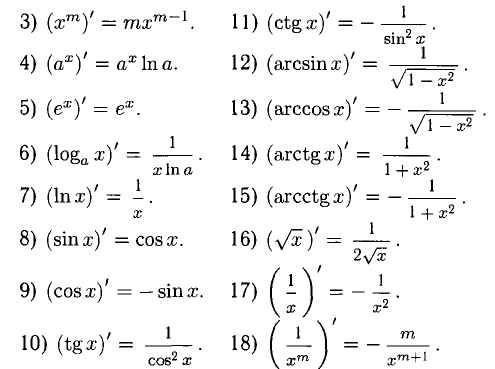
Формулы 16)-18) являются частными случаями 3). Все формулы необходимо знать наизусть.
2°. Функции, составленные из основных при помощи арифметических действий (сложения, вычитания, умножения, деления) и композиции (функция от функции), дифференцируются по правилам:
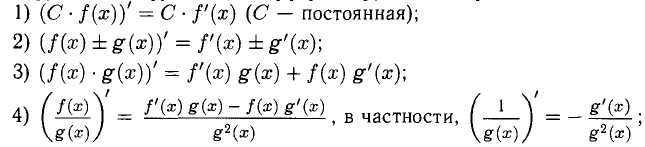
5) если f(u) и и = u(x) — дифференцируемые функции, то производная сложной функции 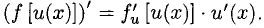
Примеры с решениями
(во всех примерах найти у’)
Пример:
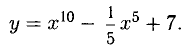
Решение:
Применяем правила 1) и 2), а также формулы 3) и 1):
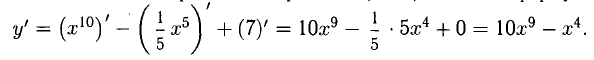
Пример:
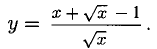
Сначала преобразуем: 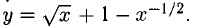
Теперь дифференцируем, используя формулы 1), 16), 3) и правила
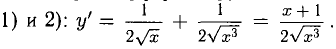
Пример:
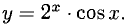
Решение:
Имеем производную произведения (правило 3)) функций, содержащихся в формулах 4) и 9):
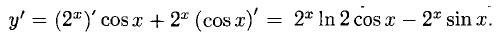
Пример:
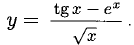
Решение:
Применяем правило 4), формулы 10), 5), 16). Производная частного:
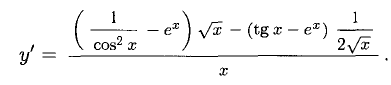
Пример:
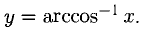
Решение:
Применяем правило 4), частный случай, и формулу 13).
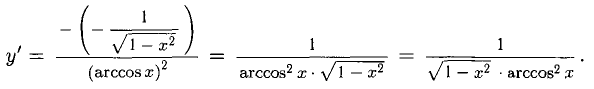
Пример:
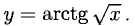
Решение:
Применяем правило 5), формулы 14) и 16). Положим
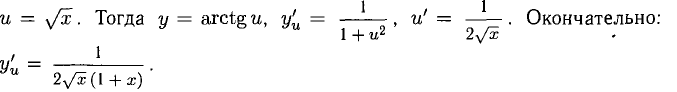
Пример:
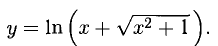
Решение:
Положим 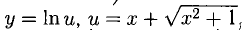 и применим правило 5). Получаем
и применим правило 5). Получаем
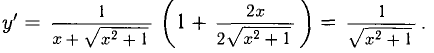
Пример:
у = cos Inx.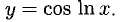
Решение:
Обозначим 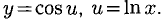 Находим
Находим
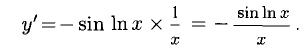
Пример:
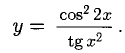
Решение:
Дифференцируем частное двух сложных функций:
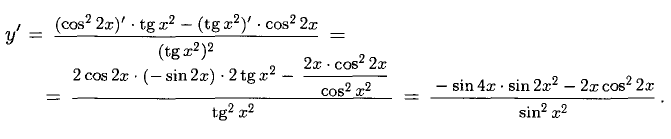
Пример:
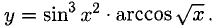
Решение:
Имеем дело с производной произведения сложных функций:
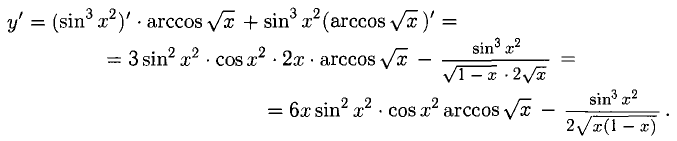
Примечание:
При дифференцировании функций, состоящих из большого количества множителей, или функций вида 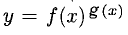 рекомендуется предварительное логарифмирование.
рекомендуется предварительное логарифмирование.
Пример:
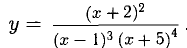
Решение:
Находим сначала ln у, затем продифференцируем обе части полученного равенства, причем левую часть lп y(х) — как сложную функцию:
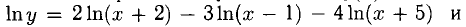
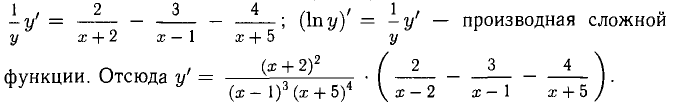
Пример:
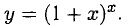
Решение:
Берем логарифм обеих частей равенства 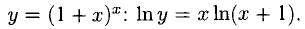 Дифференцируем:
Дифференцируем:
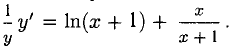
Отсюда
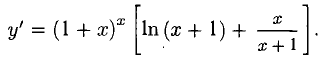
Дифференциал функции и ее линеаризация
1°. Дифференциалом дифференцируемой функции 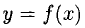 называется произведение ее производной на произвольное приращение аргумента:
называется произведение ее производной на произвольное приращение аргумента:
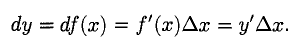
Для функции у = х ее дифференциал равен
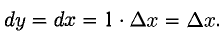
Дифференциал аргумента совпадает с его произвольным приращением, поэтому дифференциал функции записывают в виде
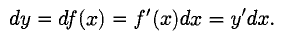
Например, если 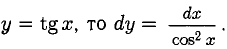
Из определения дифференциала функции можно записать новое, формальное определение производной:
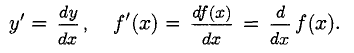
Это обозначение принято в дифференциальных уравнениях.
2°. Из рис. 7.1 видно, что 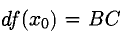 — приращение ординаты касательной при переходе точки х от
— приращение ординаты касательной при переходе точки х от 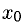 к
к 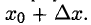 При
При 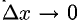 дифференциал — бесконечно малая величина. Дифференциал функции аппроксимирует приращение функции, т.е. если
дифференциал — бесконечно малая величина. Дифференциал функции аппроксимирует приращение функции, т.е. если 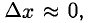 то
то
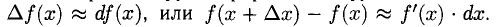
Отсюда получаем приближенное равенство
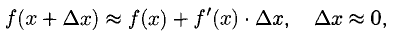
которое называется линеаризацией функции f(x) в точке х. Геометрически это означает замену дуги Г графика функции f(x) отрезком касательной t, что возможно при достаточно малых 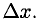
3°. Линеаризацию функции в фиксированной точке 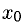 можно использовать в приближенных вычислениях:
можно использовать в приближенных вычислениях:
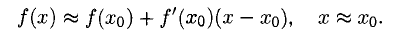
Примеры с решениями
Пример:
Вычислить приближенно значение функции 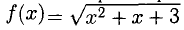 при х = 1,97.
при х = 1,97.
Решение:
Принимаем 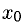 = 2. Тогда
= 2. Тогда 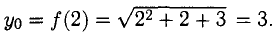 Далее,
Далее,
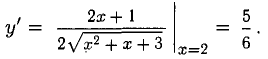
Так как 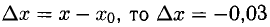 и, согласно формуле п. 3°, имеем
и, согласно формуле п. 3°, имеем
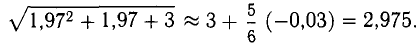
Пример:
Вычислить приближенно увеличение объема цилиндра с высотой H = 40 см и радиусом основания R = 30 см при увеличении радиуса на 0,5 см.
Решение:
Объем цилиндра V при постоянной высоте H и переменном радиусе х есть функция от х: 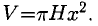 При х=R=30 имеем
При х=R=30 имеем 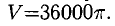 Приращение объема цилиндра заменим его дифференциалом:
Приращение объема цилиндра заменим его дифференциалом:
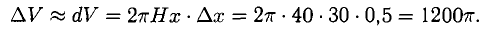
Ответ.
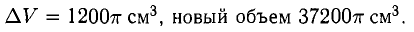
Пример:
Найти дифференциал функции 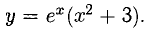 Вычислить величину дифференциала в точке х = 0.
Вычислить величину дифференциала в точке х = 0.
Решение:
Имеем:
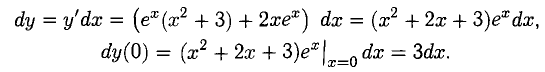
Производные и дифференциалы высших порядков
1°. Предположим, что производная 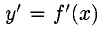 функции
функции 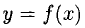 есть дифференцируемая функция. Тогда ее производная
есть дифференцируемая функция. Тогда ее производная 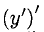 называется второй производной функции
называется второй производной функции 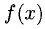 и обозначается
и обозначается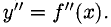 Производные высших порядков определяются последовательно:
Производные высших порядков определяются последовательно: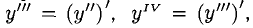 Обозначения могут быть также:
Обозначения могут быть также: 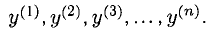
Например, если
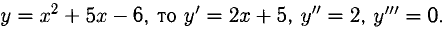
Если у = cosx, то производную любого порядка этой функции найдем следующим образом:
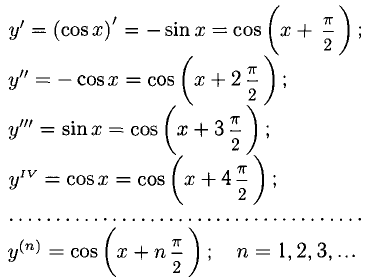
2°. Дифференциалы высших порядков определяются так:
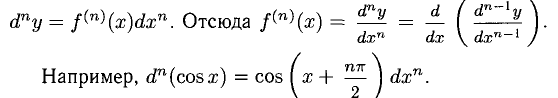
Дифференцирование обратных функций. Дифференцирование функций, заданных неявно и параметрически
1°. Пусть у = f (х) — функция, определенная и непрерывная на отрезке [а; b] и f (а) = A, f(b) = В. Если различным значениям 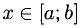 соответствуют разные значения
соответствуют разные значения 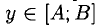 (или
(или 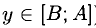 ), то функция у= f (х) обратима, т.е. имеет обратную функцию, обозначаемую
), то функция у= f (х) обратима, т.е. имеет обратную функцию, обозначаемую 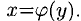 При этом
При этом 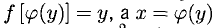 непрерывна на отрезке [А; В].
непрерывна на отрезке [А; В].
Например, функция 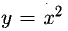 обратима на каждом из двух лучей
обратима на каждом из двух лучей 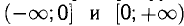 , при этом
, при этом 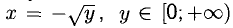 и
и 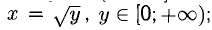
у = tgx обратима в интервале 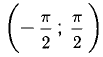 или в любом другом интервале
или в любом другом интервале 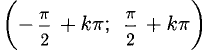 , где k — фиксированное целое число при этом х = arctg у или
, где k — фиксированное целое число при этом х = arctg у или 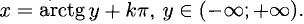
2°. Если различным значениям 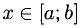 соответствует одно значение
соответствует одно значение 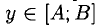 , то функция у = f (х) имеет несколько обратных функций.
, то функция у = f (х) имеет несколько обратных функций.
Например, непрерывная функция 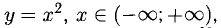 имеет две непрерывные обратные функции
имеет две непрерывные обратные функции 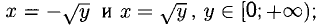 непрерывная функция
непрерывная функция 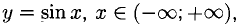 имеет бесконечное множество непрерывных обратных функций
имеет бесконечное множество непрерывных обратных функций
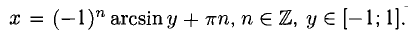
3°. Если у = f(x) дифференцируема на отрезке [а; b] и 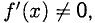 то обратная функция
то обратная функция 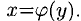 также дифференцируема на [А; В] и
также дифференцируема на [А; В] и
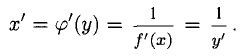
Например, пусть 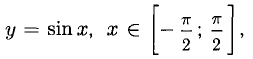 тогда
тогда 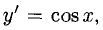 для
для
обратной функции 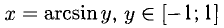 имеем
имеем
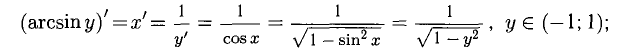
при у = ±1 имеем
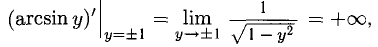
это согласуется с тем, что 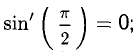
если 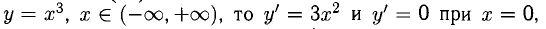 для обратной функции
для обратной функции 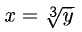 имеем
имеем 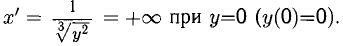
4°. Если у как функция от x задается соотношением F(x,y) = 0, то у называется неявной функцией от x, в отличие от явного способа задания у = f(x) . Производная от у по x: при неявном способе задания функции может быть определена дифференцированием выражения F(x, у) = 0 как сложной функции, считая у функцией от х; решая полученное уравнение относительно производной 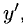 находим выражение производной от неявной функции в виде
находим выражение производной от неявной функции в виде 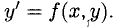
5°. Если функция у = у(х) задается параметрически, т.е. при помощи двух функций 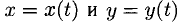 аргумента t, a x (t) и y(t) — дифференцируемые функции, то производную у’ = у'(х), обозначаемую еще
аргумента t, a x (t) и y(t) — дифференцируемые функции, то производную у’ = у'(х), обозначаемую еще 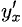 , находим при помощи дифференциалов:
, находим при помощи дифференциалов:
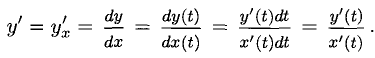
Вторую производную 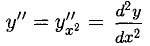 можно найти при помощи одной из двух формул (они основаны на производной сложной функции, дроби и обратной функции
можно найти при помощи одной из двух формул (они основаны на производной сложной функции, дроби и обратной функции 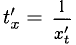 ):
):
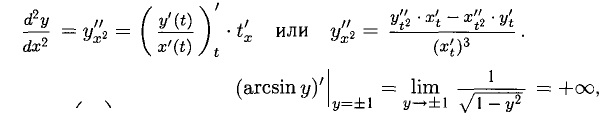
Примеры с решениями
Пример:
Найти у’, если 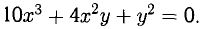 Найти также у’ при х = -2, у = 4.
Найти также у’ при х = -2, у = 4.
Решение:
Считаем, что у = у(х). Продифференцируем левую часть данного уравнения как сложную функцию, приравняем нулю полученное выражение и найдем у’:
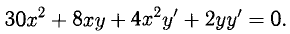
Отсюда 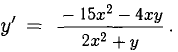 Подставляя х = -2, у = 4, получаем
Подставляя х = -2, у = 4, получаем 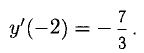
Пример:
Найти у’, если 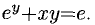 Найти также у'(0).
Найти также у'(0).
Решение:
Дифференцируем обе части данного равенства, имея в виду, что 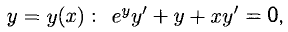 откуда находим
откуда находим 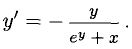
В частности, если х = 0, то у =1 и 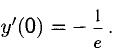
Пример:
Для функции у(х), определенной неявно уравнением 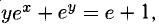 найти у».
найти у».
Решение:
После двух последовательных дифференцирований данного уравнения с учетом у = у (х) получаем
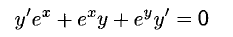
и
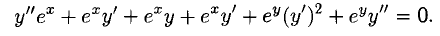
Из второго равенства находим
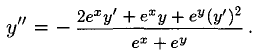
Из первого равенства находим
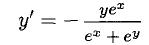
и подставляем это в предыдущее равенство. После упрощения получаем
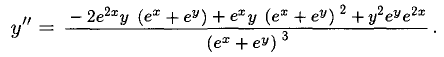
Пример:
Найти у’ и у», если 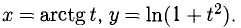
Решение:
Имеем:
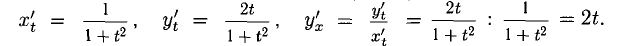
При помощи первой из формул для 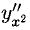 находим
находим
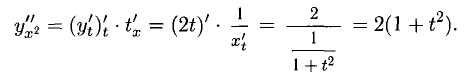
Пример:
Найти у», если х = ln t, у = sin2t
Решение:
Для определения у» будем использовать вторую формулу. Сначала находим:
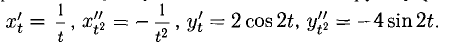
Следовательно,
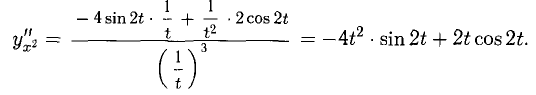
Основные теоремы дифференциального исчисления
1°. Точка 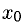 называется точкой относительного максимума (минимума) функции f (х), если в некоторой окрестности этой точки имеет место неравенство
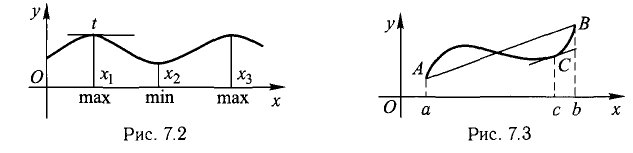
называется точкой относительного максимума (минимума) функции f (х), если в некоторой окрестности этой точки имеет место неравенство 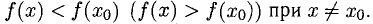 Точки относительного максимума и минимума f(x) называются точками экстремума, а значения в этих точках — экстремальными значениями. На рис. 7.2 изображен график функции с тремя экстремумами.
Точки относительного максимума и минимума f(x) называются точками экстремума, а значения в этих точках — экстремальными значениями. На рис. 7.2 изображен график функции с тремя экстремумами.
Теорема Ферма:
Если дифференцируемая функция f(x) имеет экстремум в точке 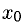 ,
, 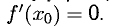
В точке экстремума касательная горизонтальна, а для нее 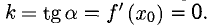
Теорема Ролля:
Предположим, что функция f(x) непрерывна на отрезке [а,b], дифференцируема в интервале (а,b) и f(a) = f (b). Тогда существует хотя бы одна точка 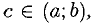 , в которой f ‘(с) = 0. Такая функция либо постоянная, т.е. f(x) = С, и тогда f'(x) = 0, х
, в которой f ‘(с) = 0. Такая функция либо постоянная, т.е. f(x) = С, и тогда f'(x) = 0, х 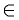 [а; b], либо имеет хотя бы одну точку экстремума с
[а; b], либо имеет хотя бы одну точку экстремума с 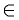 (а; b), и тогда f ‘(с) = 0.
(а; b), и тогда f ‘(с) = 0.
Теорема Лагранжа:
Предположим, что функция f(x) непрерывна на отрезке [а; b] и дифференцируема в интервале (а; b). Тогда существует хотя бы одна точка с € (а; b), такая, что f(b)-f(a)=f'(c)(b-a), или 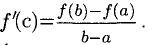
Геометрически теорема 4 означает что на кривой существует хотя бы одна точка, в которой касательная параллельна хорде АВ, f ‘(с) — ее угловой коэффициент (рис. 7.3).
Теорема Коши:
Пусть f(x) и g(x) — две функции, непрерывные на отрезке [а; b] и дифференцируемые в интервале (а; b), причем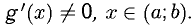 . Тогда существует хотя бы одна точка, такая, что
. Тогда существует хотя бы одна точка, такая, что
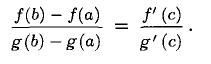
Примеры с решениями
Пример:
Проверить, справедлива ли теорема Ролля для функции 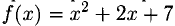 на отрезке [-6; 4], и если да, то найти соответствующее значение с.
на отрезке [-6; 4], и если да, то найти соответствующее значение с.
Решение:
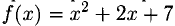 непрерывна и дифференцируема на любом отрезке, в частности, на [—6; 4], и f (6) = f (4) = 31. Значит, f'(x) = 2х + 2 = 0 при некотором х € (-6; 4). Имеем х = с = — 1.
непрерывна и дифференцируема на любом отрезке, в частности, на [—6; 4], и f (6) = f (4) = 31. Значит, f'(x) = 2х + 2 = 0 при некотором х € (-6; 4). Имеем х = с = — 1.
Пример:
Найти точку с, о которой идет речь в теореме Лагранжа, для функции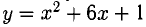 на отрезке [-1;3].
на отрезке [-1;3].
Решение:
Имеем у(-1) = -4, у(3) = 28, A(-1,-4), B(3,28), 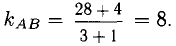
Нам надо решить уравнение у’ = 2x + 6 = 8. Находим х = 1, т. е. с имеет координаты (1,8). Касательная в этой точке параллельна хорде АВ.
Пример:
Составить уравнения касательной и нормали к кривой у = х ln х , проведенных в точке с абсциссой х = е.
Решение:
Имеем:
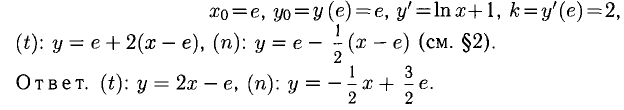
Пример:
Составить уравнения касательной и нормали к кривой 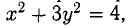 проведенных в точке с ординатой у = 1 и отрицательной абсциссой.
проведенных в точке с ординатой у = 1 и отрицательной абсциссой.
Решение:
При у = 1 находим х = —1 и х = 1. В задаче идет речь о точке A(-1,1). Находим у’ из уравнения 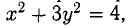 . Имеем
. Имеем 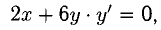 отсюда
отсюда 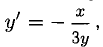 а значит, подставляя сюда х =- 1, y=1 получаем
а значит, подставляя сюда х =- 1, y=1 получаем 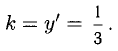
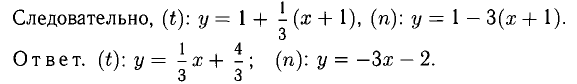
Пример:
Составить уравнения касательной и нормали к эллипсу 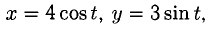 проведенных в точке, получаемой при
проведенных в точке, получаемой при 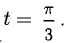
Решение:
Имеем:
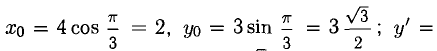
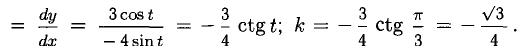
Следовательно,
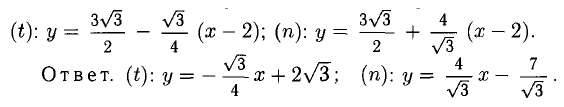
Исследование на монотонность и экстремум
1°. Предположим, что функция f(x) непрерывна в интервале (а; b) и 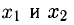 — любые две точки этого интервала, причем
— любые две точки этого интервала, причем 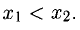
Функция f(x) называется в этом интервале:
— возрастающей (неубывающей), если
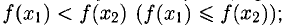
— убывающей (невозрастающей), если
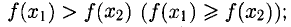
— монотонной, если она либо возрастающая (неубывающая), либо убывающая (невозрастающая).
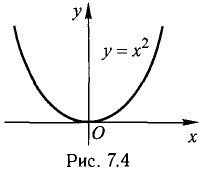
Например, функция 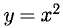 в интервале
в интервале 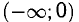 монотонно убывает, в
монотонно убывает, в 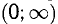 монотонно возрастает, в
монотонно возрастает, в 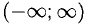 не является монотонной (рис. 7.4).
не является монотонной (рис. 7.4).
Теорема:
Если f ‘(х) > 0 при 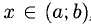 , то f (х) монотонно возрастает в этом интервале. Если f'(x) < 0,
, то f (х) монотонно возрастает в этом интервале. Если f'(x) < 0, 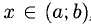 , то f(x) монотонно убывает в этом интервале.
, то f(x) монотонно убывает в этом интервале.
2°. Следующие две теоремы выражают достаточные условия для того, чтобы данная точка хо была экстремальной для дифференцируемой функции f(x).
Теорема:
Если при 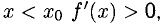 а при
а при 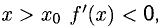 то
то 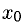 — точка максимума функции f (х). Если при
— точка максимума функции f (х). Если при 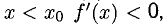 а при
а при 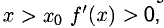 то
то 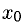 — точка минимума функции f (х).
— точка минимума функции f (х).
Точки, в которых производная непрерывной функции равна 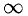 или не существует, называются критическими. Точки, в которых f ‘(х) = 0, называются стационарными.
или не существует, называются критическими. Точки, в которых f ‘(х) = 0, называются стационарными.
Если непрерывная функция f (х) имеет экстремум в точке 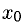 то эта точка — критическая для этой функции.
то эта точка — критическая для этой функции.
Теорема:
Если 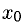 — стационарная точка, то при
— стационарная точка, то при 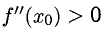 — точка минимума, а при
— точка минимума, а при 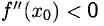
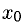 — точка максимума.
— точка максимума.
Примеры с решениями
Пример:
Исследовать на монотонность и экстремумы функцию 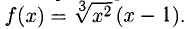
Решение:
f (x) определена при всех 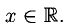 По формуле производной произведения
По формуле производной произведения
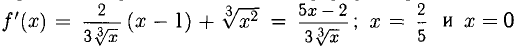
— критические точки f (х). На верхней оси диаграммы (рис. 7.5) обозначено распределение знаков f ‘(х), а на нижней — поведение функции f (х) согласно теоремам 6 и 7.
Ответ. В интервалах 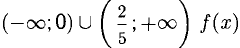 монотонно возрастает
монотонно возрастает 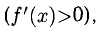 в интервале
в интервале 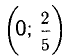 монотонно убывает, х = 0 — точка максимума с
монотонно убывает, х = 0 — точка максимума с 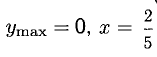 точка минимума с
точка минимума с 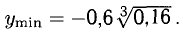
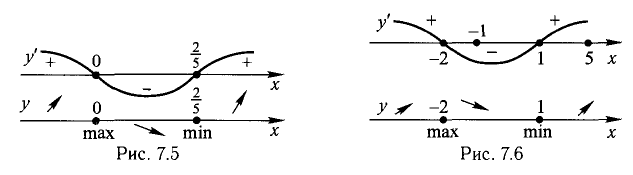
Пример:
Исследовать на монотонность и экстремумы функцию 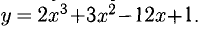 Найти также наибольшее и наименьшее значения этой функции на отрезке [—1;5].
Найти также наибольшее и наименьшее значения этой функции на отрезке [—1;5].
Решение:
Находим у’ и исследуем ее знак:
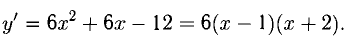
Знаки у’ и области монотонности изображены на диаграмме (рис. 7.6); х = -2, х = 1 — стационарные точки, х = 1 — точка минимума, х = -2 — точка максимума. При этом 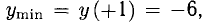
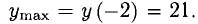 Эти значения — экстремальные. Вычислим еще
Эти значения — экстремальные. Вычислим еще 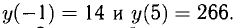
Ответ. Функция монотонно возрастает в 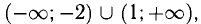 убывает в (-2;1), имеет максимум при х = -2,
убывает в (-2;1), имеет максимум при х = -2,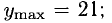 имеет минимум при x=1,
имеет минимум при x=1, 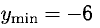 — наименьшее значение; наибольшее —
— наименьшее значение; наибольшее —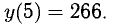
Раскрытие неопределенностей
1°. Неопределенности видов 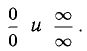
Пусть функции f(x) и g(x) непрерывны и дифференцируемы в некоторой окрестности точки х = а, кроме, быть может, самой точки а (при этом а может быть конечным числом или 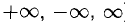 ). Предположим, что
). Предположим, что
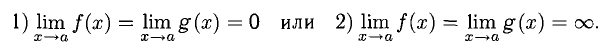
Правило Лопиталя. Если существует предел 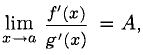 то существует и предел
то существует и предел 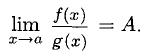
Правило Лопиталя позволяет при помощи производных раскрыть неопределенность: в случае 1) вида 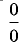 , а в случае 2) — вида
, а в случае 2) — вида 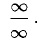
При необходимости правило Лопиталя можно применить повторно или несколько раз при соответствующих условиях на 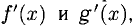
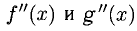 и т.д.
и т.д.
Например, вычислим пределы:
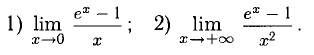
В первом случае имеем неопределенность вида 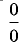 , во втором —
, во втором —
вида 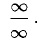 . В том и другом случае условия применимости правил Лопиталя удовлетворяются. Переход к производным по ходу решения примеров будем отмечать знаком
. В том и другом случае условия применимости правил Лопиталя удовлетворяются. Переход к производным по ходу решения примеров будем отмечать знаком 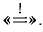 . Переходим к вычислениям, замечая заранее, что во втором примере правило Лопиталя применим дважды.
. Переходим к вычислениям, замечая заранее, что во втором примере правило Лопиталя применим дважды.
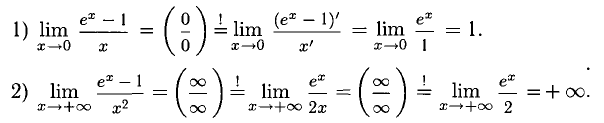
2°. При помощи правила Лопиталя можно раскрыть неопределенности других видов: 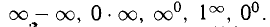 Для этого исходные выражения необходимо приводить к виду
Для этого исходные выражения необходимо приводить к виду 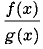 .
.
В нижеследующих примерах необходимые преобразования выполним по ходу решения. Заметим, что иногда приходится избавляться от «мешающих» множителей — это делается при помощи теоремы о пределе произведения.
Примеры с решениями
Пример:
Вычислить пределы:
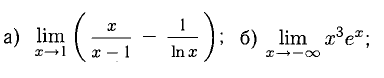
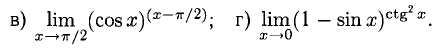
Визуальный обзор указывает на наличие разных неопределенностей.
Решение:
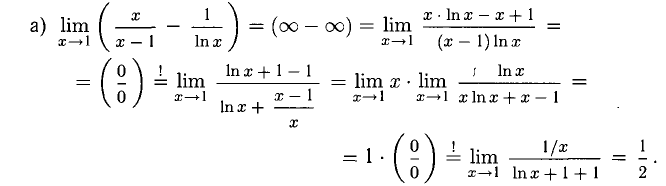
Здесь мы избавились от множителя х, усложняющего производную, и дважды применили правило Лопиталя.
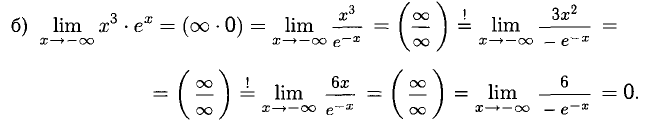
Рекомендуем вычислить этот предел при помощи замены х = —t 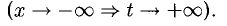
в) Найдем предел логарифма выражения, стоящего под знаком предела. Воспользуемся теоремой о возможности перехода к пределу под знаком непрерывной функции:
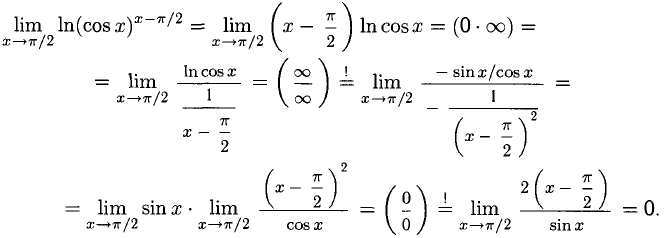
Вывод: искомый предел равен е° = 1.
г) Этот пример, как и предыдущий, можно решить при помощи основного показательно-логарифмического тождества: 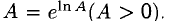 Следовательно,
Следовательно,
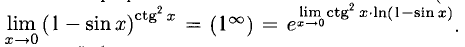
Для компактности выражений берем отдельно предел показателя:
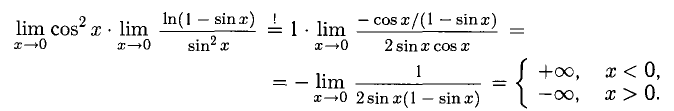
Получили два различных односторонних предела, следовательно, искомый предел не существует. Тем не менее зафиксируем односторонние пределы:
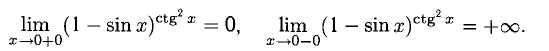
Асимптоты
Вертикальные асимптоты
Напомним, что если х = а — точка разрыва функции f(x) и 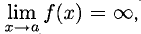 то прямая х = а называется вертикальной асимптотой графика этой функции.
то прямая х = а называется вертикальной асимптотой графика этой функции.
Примеры с решениями
Требуется определить точки разрыва данной функции, исследовать их характер, найти вертикальные асимптоты и построить график в окрестности точки разрыва.
Пример:
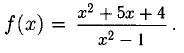
Решение:
х = -1 и х = 1 — точки разрыва. Имеем:
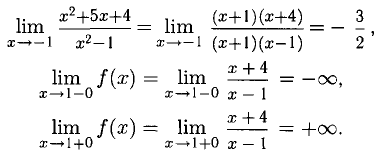
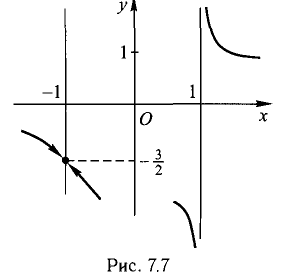
Ответ, x = -1 — точка устранимого разрыва, х = 1 — точка разрыва второго рода. График построен (рис. 7.7), х = 1 — вертикальная асимптота вверх и вниз.
Пример:
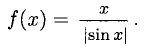
Решение:
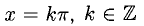 — точки разрыва. Рассмотрим отдельно
— точки разрыва. Рассмотрим отдельно 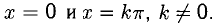
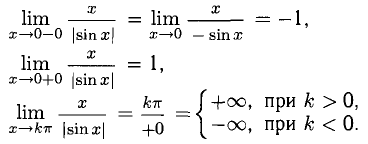
Ответ, x = 0 — точка разрыва первого рода со скачком 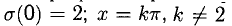 — точки разрыва второго рода. Прямые
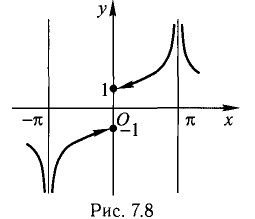
— точки разрыва второго рода. Прямые 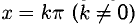 — вертикальные асимптоты: вверх при k > 0, вниз — при k < 0 (рис. 7.8).
— вертикальные асимптоты: вверх при k > 0, вниз — при k < 0 (рис. 7.8).
Пример:
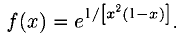
Решение:
x = 0 и x = 1 — точки разрыва,
Ответ, х = 0, х =01 — точки разрыва второго рода, прямые х = 0, х = 1 — вертикальные асимптоты (рис. 7.9).
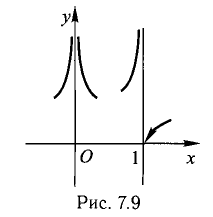
Наклонные асимптоты. Горизонтальные асимптоты
Прямая с уравнением у = kx + b называется наклонной асимптотой графика функции f(x), если 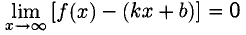 (возможно
(возможно 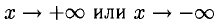
После деления на х выражения, стоящего под знаком предела, и перехода к пределу получаем
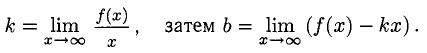
Горизонтальная асимптота является частным случаем наклонной при 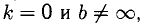 т. е. это прямая у = b, если
т. е. это прямая у = b, если 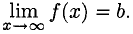
Примеры с решениями
Требуется найти наклонные асимптоты графика данной функции, если они есть.
Пример:
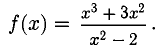
Решение:
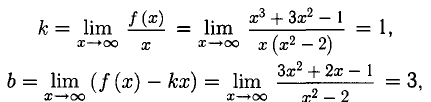
y = х + 3 — наклонная асимптота.
Пример:
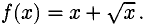
Решение:
Функция определена только при 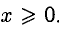 Наклонной асимптоты нет, поскольку
Наклонной асимптоты нет, поскольку
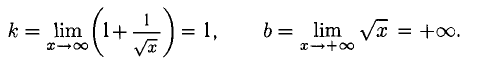
Пример:
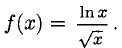
Решение:
Данная функция определена при x > 0, поэтому 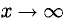 означает
означает 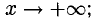
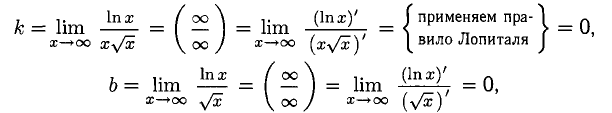
у = 0 — горизонтальная асимптота (вправо, 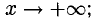 ).
).
Исследование функций на выпуклость, вогнутость и перегиб при помощи второй производной
1°. Дифференцируемая функция f (х) называется выпуклой (вогнутой) в некотором интервале, если ее график расположен ниже (выше) касательной, проведенной в каждой его точке с абсциссой в этом интервале.
Теорема:
Если f»(x) < 0 при всех 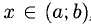 , то в этом интервале f (x) выпуклая. Если f «(ж) > 0,
, то в этом интервале f (x) выпуклая. Если f «(ж) > 0, 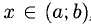 , то f(x) вогнутая в (а; b).
, то f(x) вогнутая в (а; b).
2°. Точка 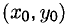 графика непрерывной функции f(x), отделяющая участок выпуклости от участка вогнутости, называется точкой перегиба.
графика непрерывной функции f(x), отделяющая участок выпуклости от участка вогнутости, называется точкой перегиба.
Теорема:
Если f»(x) < 0 при 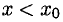 и f»(x) > 0 при
и f»(x) > 0 при 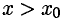 или наоборот, то
или наоборот, то 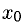 — абсцисса точки перегиба функции f(x).
— абсцисса точки перегиба функции f(x).
Следует из теоремы 9.
Примеры с решениями
Пример:
Исследовать на выпуклость, вогнутость и перегиб функцию 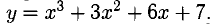
Решение:
Имеем: 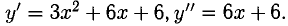 Знаки у» указаны на числовой прямой.
Знаки у» указаны на числовой прямой.
Ответ. В интервале 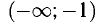 f(x) выпуклая, в интервале
f(x) выпуклая, в интервале 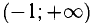 f(x) вогнутая, х = -1 — абсцисса точки перегиба (рис. 7.10) и
f(x) вогнутая, х = -1 — абсцисса точки перегиба (рис. 7.10) и 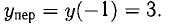
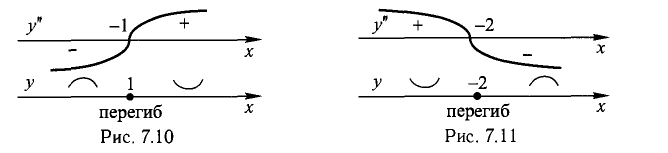
Пример:
Исследовать на выпуклость, вогнутость и перегиб функцию 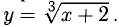
Решение:
Надлежит исследовать знак второй производной.
Имеем:
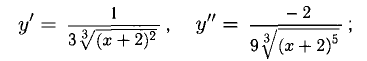
у» нигде не обращается в нуль, но меняет знак в точке х = -2. Знаки у» указаны на диаграмме; здесь же указан вид графика (рис. 7.11): х = — 2 — абсцисса точки перегиба, 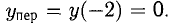 На
На 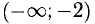 функция у вогнутая, на
функция у вогнутая, на 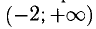 выпуклая.
выпуклая.
Применение высших производных
1°. Запись 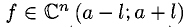 означает, что функция f(x) непрерывна в интервале
означает, что функция f(x) непрерывна в интервале 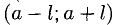 вместе со всеми ее производными порядка 1,2, …п включительно, п € N.
вместе со всеми ее производными порядка 1,2, …п включительно, п € N.
2°. Многочлен степени не выше п
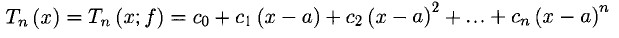
называется многочленом Тейлора функции f(x) с центром в точке х = а, если его коэффициенты 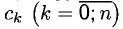 вычисляются по формулам
вычисляются по формулам
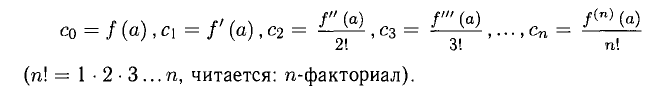
Теорема Тейлоро:
Если 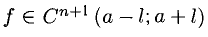 , то имеет место равенство
, то имеет место равенство
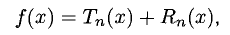
где
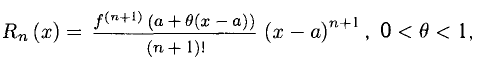
— остаточный член формулы Тейлора в форме Лагранжа. Величина Rn(x) — бесконечно малая порядка (п+1) относительно (х — а) в окрестности точки а.
При а = 0 многочлен Тейлора называется также многочленом Маклорена. Многочлен Тейлора-Маклорена служит достаточно хорошим средством приближенного представления функции и широко применяется в приближенных вычислениях.
3°. Многочлены Маклорена для некоторых из элементарных функций имеют следующий вид (рекомендуется получить их и знать).
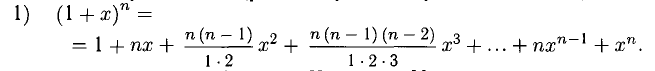
Эта формула называется биномом Ньютона. Множители
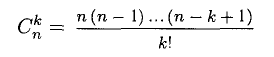
— биномиальные коэффициенты — находят широкое применение в комбинаторике и теории вероятностей.
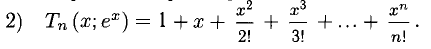
При этом
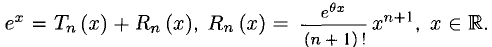
Здесь и далее 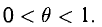
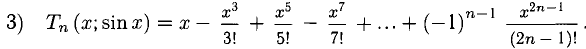
При этом
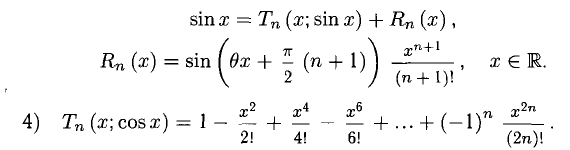
При этом
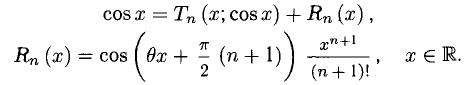
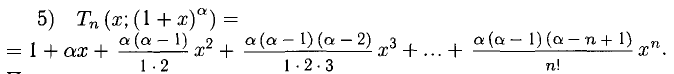
При этом
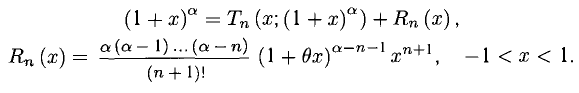
Примеры с решениями
Пример:
Вычислить с точностью до 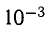 значение sin20°.
значение sin20°.
Решение:
Имеем
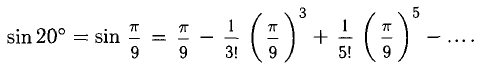
Число членов в правой части следует брать из условия 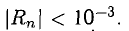
Для п = 3 имеем
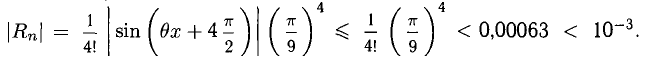
Следовательно,
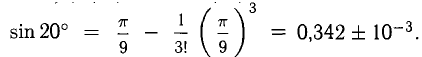
Ответ.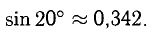
Пример:
Многочлен 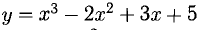 разложить по целым положительным степеням бинома х — 2.
разложить по целым положительным степеням бинома х — 2.
Решение:
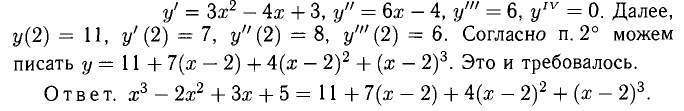
Пример:
Написать многочлен Тейлора третьей степени с центром в точке х = 3 для функции 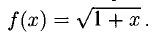
Решение:
Имеем
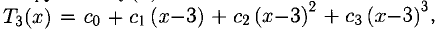
где 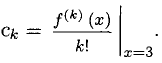 Сначала найдем производные:
Сначала найдем производные:
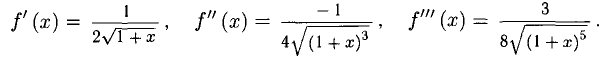
Вычислим теперь 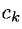 .
.
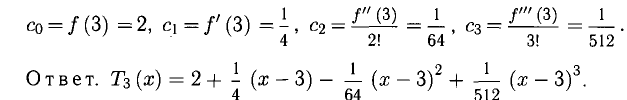
Исследование функций и построение графиков
Построению графика данной функции у = f (х) предшествует полное ее исследование, включающее выявление характерных свойств и особенностей этой функции. К ним относятся: область определения D = D ( f ), область изменения E(f), непрерывность, дифференцируемость, четность, нечетность, ограниченность, периодичность функции, ее интервалы знакопостоянства, монотонности, выпуклости/вогнутости, наличие асимптот (вертикальных, горизонтальных, наклонных). Кроме этого, необходимо определить характерные точки: разрыва, пересечения графика с координатными осями, точки экстремума (максимума, минимума), точки перегиба и проч.
Приведем сначала определения тех понятий, которые не встречались выше.
Напомним, что функция у = f (х) называется:
- четной, если
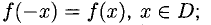
- нечетной, если
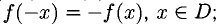
- ограниченной сверху (снизу), если существует число М (m), такое, что
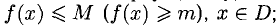
- ограниченной, если она ограничена и сверху, и снизу;
— периодической, если существует число Т > 0, такое, что 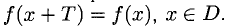
Исследование функции выполняется по определенной схеме, пункты которой установим по ходу исследования. Заметим, что если по некоторым признакам мы не имеем позитивной информации, то соответствующий пункт может быть опущен.
Примеры построения графиков
Пример:
Исследовать функцию 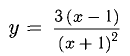 и построить ее график.
и построить ее график.
1) Находим область определения:
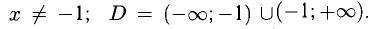
2) Простейшие свойства — четность, нечетность, периодичность, ограниченность. Таких свойств не обнаруживаем.
3) Определим точки пересечения графика с координатными осями и интервалы знакопостоянства функции.
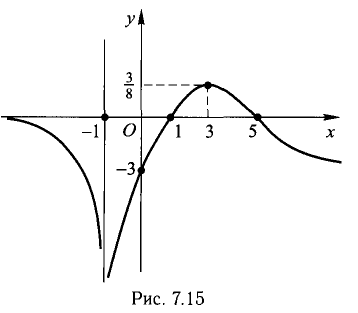
Положим у = 0. Находим х = 1. Положим х = 0 и находим у = -3. Точки A(1,0) и В(0, -3) лежат на Ох и Оу соответственно и на графике функции. Знаки f(x) изображены на диаграмме (рис. 7.12).
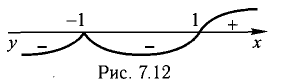
4) Исследуем точку разрыва х = — 1. Имеем: 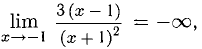 х = -1 — вертикальная асимптота вниз.
х = -1 — вертикальная асимптота вниз.
5) Исследуем функцию на монотонность и экстремум (рис. 7.13):
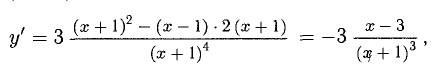
х = 3 — точка max, 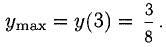 В интервалах
В интервалах 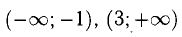 функция убывает, а в интервале (— 1; 3) она возрастает.
функция убывает, а в интервале (— 1; 3) она возрастает.
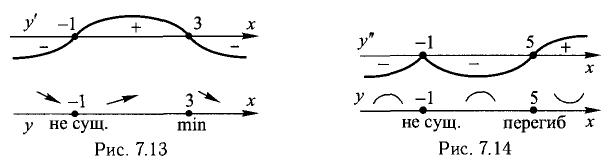
Везде «не сущ.» означает «не существует».
6) Исследуем на выпуклость, вогнутость и перегиб (рис. 7.14)
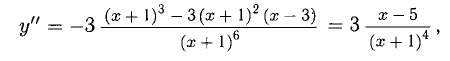
х = 5 — абсцисса точки перегиба, 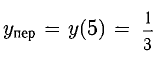 . В интервалах
. В интервалах 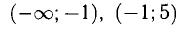 функция выпуклая, а в интервале
функция выпуклая, а в интервале 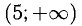 — вогнутая.
— вогнутая.
7) Исследуем поведение функции на бесконечности и определим горизонтальные и (или) наклонные асимптоты. Имеем: 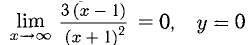 — горизонтальная асимптота в обе стороны.
— горизонтальная асимптота в обе стороны.
8) Результаты исследования поместим в таблицу для компактности:
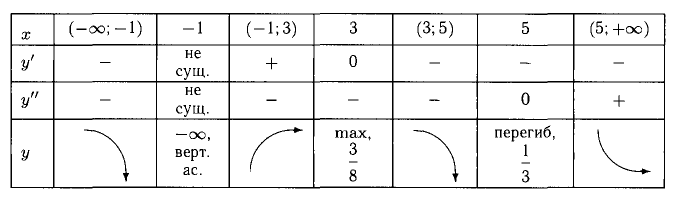
В первую строку таблицы заносим точки разрыва, экстремума, перегиба и интервалы между ними. Во второй строке располагается
информация о f'(x) и ее знаках, в третьей строке о f»(x) и ее знаках. Третья строка показывает вид графика в соответствующих интервалах и характерные его точки.
9) Построение графика начинается с построения асимптот и точек с известными координатами (рис. 7.15). Приближение графика к асимптоте должно быть плавным и создавать впечатление неограниченного продолжения.
Пример:
Исследовать функцию 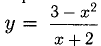 построить ее график.
построить ее график.
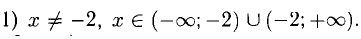
2) График пересекает ось Ох, если 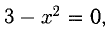 т.е. при
т.е. при 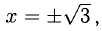 а ось Оу при
а ось Оу при 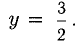 Интервалы знакопостоянства обозначены на рис. 7.16 «волной» знаков функции
Интервалы знакопостоянства обозначены на рис. 7.16 «волной» знаков функции 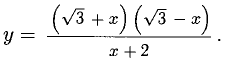
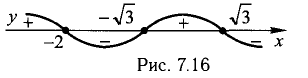
3) Исследуем точку разрыва х = -2. Находим односторонние пределы
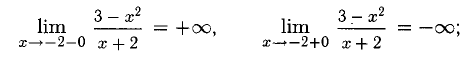
х =-2 — вертикальная асимптота вверх и вниз.
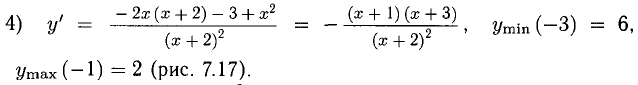
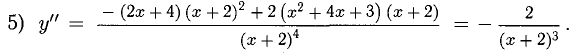
Точек перегиба нет, схема выпуклости/вогнутости представлена на рис. 7.18.
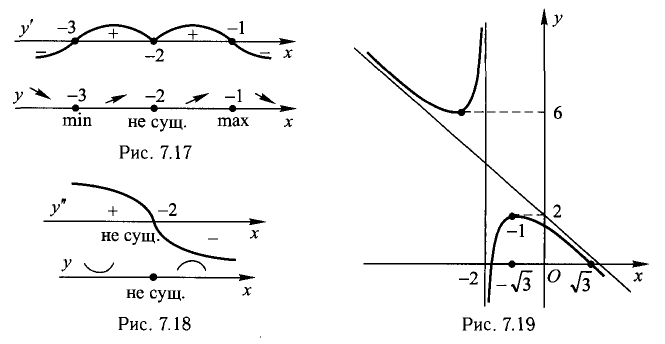
6) Имеем 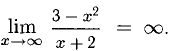 Горизонтальной асимптоты нет. Далее,
Горизонтальной асимптоты нет. Далее,
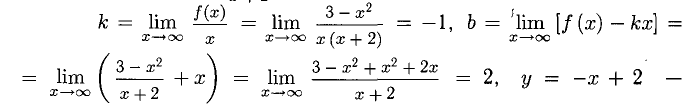
уравнение наклонной асимптоты в обе стороны.
7) Таблица:
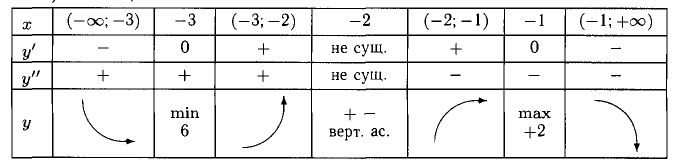
8. График построен (рис. 7.19).
Примечание. Последовательность действий может быть изменена (вертикальные асимптоты можно искать параллельно с горизонтальными и наклонными), а некоторые пункты схемы могут быть опущены, если это не влияет на выводы исследования.
Пример:
Исследовать функцию 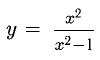 и построить ее график.
и построить ее график.
Укажем основные элементы исследования и приведем график.
1) 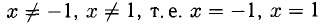 — точки разрыва.
— точки разрыва.
2) Функция четная, так как 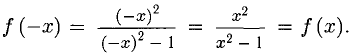
График функции симметричен относительно оси Оу.
3) 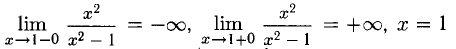 — вертикальная
— вертикальная
асимптота вниз и вверх (х =-1 — вертикальная асимптота вверх и вниз, по четности).
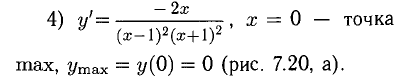
5) 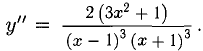
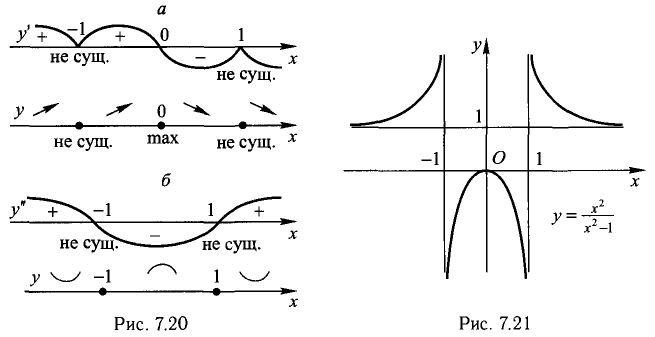
Точек перегиба нет, схема выпуклости/вогнутости представлена на рис. 7.20, б.
6) 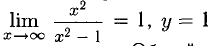 — горизонтальная асимптота. Общий вид функции показан на рис. 7.21.
— горизонтальная асимптота. Общий вид функции показан на рис. 7.21.
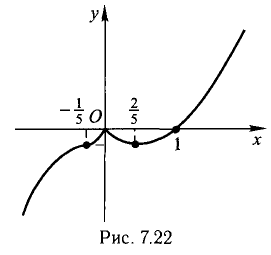
Пример:
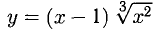 (рис. 7.22).
(рис. 7.22).
Указание,
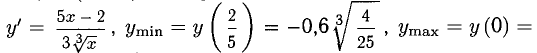
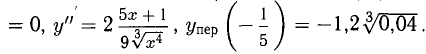
Никаких асимптот нет.
Пример:
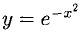 — четная, х € R (рис. 7.23).
— четная, х € R (рис. 7.23). 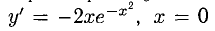 — точка максимума,
— точка максимума, 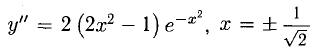 точка перегиба,
точка перегиба, 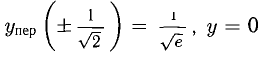 — горизонтальная асимптота.
— горизонтальная асимптота.
Пример:
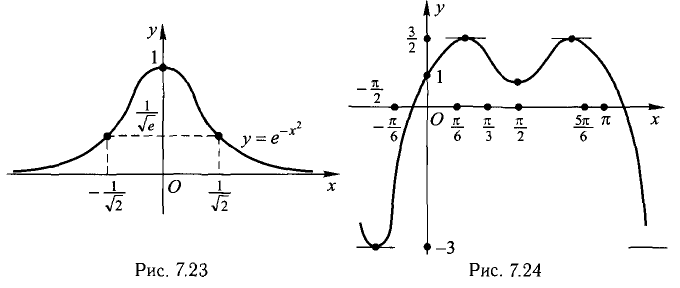
у = 2 sin x + cos2x (рис. 7.24).
Функция определена при 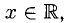 имеет период
имеет период
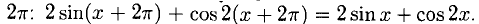
Исследование на экстремум проводим по такому признаку. Если 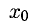 — стационарная точка и
— стационарная точка и 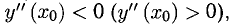 то
то 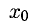 — точка mах (min).
— точка mах (min).
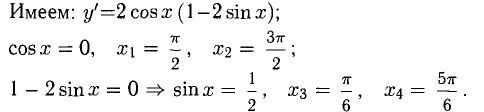
Функция имеет 4 стационарных точки: 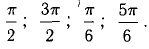 Определим знак у» в них:
Определим знак у» в них:
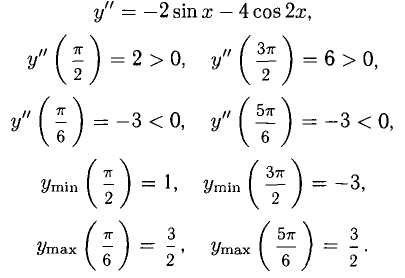
Функция не имеет асимптот.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

