Арифметический квадратный корень в математике с примерами решения и образцами выполнения

Определение:

Арифметическим квадратным корнем из положительного числа а называется такое положительное число х, квадрат которого равен а.

Например, арифметическим квадратным корнем из 49 будет число 7, так как 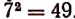. Квадратный корень из единицы равен единице.

Арифметический квадратный корень из числа а обозначается символом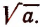

Примеры:

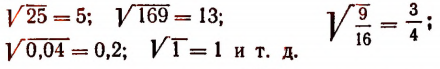
По определению из равенства 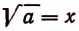следует, что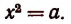

Извлечение квадратного корня является действием, обратным возведению в квадрат.

Квадратный корень из 0 равен 0.

В дальнейшем (см. гл. XXXIV) рассматриваются квадратные и другие корни в более расширенном (алгебраическом) смысле.

Извлечение арифметического квадратного корня из многозначных натуральных чисел, представляющих собой точные квадраты

Прежде всего обратим внимание на следующую таблицу:

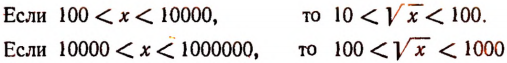
и т.д.

Из этой таблицы можно сделать следующее заключение.

Если натуральное число, представляющее точный квадрат, выражается с помощью одной или двух цифр, то квадратный корень из него будет выражаться одной цифрой.
Например:

Если число выражается с помощью трех или четырех цифр, то квадратный корень из него будет число двузначное.
Например:

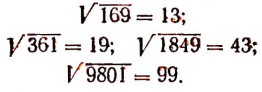
Если число выражается с помощью пяти или шести цифр, то квадратный корень из него будет число трехзначное и т. д.
Например:

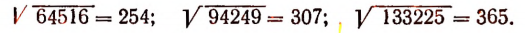
Вывод правила извлечения квадратного корня из натурального числа, представляющего точный квадрат

Предполагая, что число 7569 есть точный квадрат, мы можем утверждать, что будет числом двузначным. Обозначим число десятков этого двузначного числа буквой х, а число единиц—буквой у. Тогда

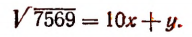
По определению корня получим

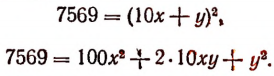
Целых сотен содержится в левой части 75, а в правой либо 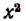, либо больше. Поэтому

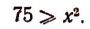
Значит, 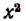есть точный квадрат, содержащийся в числе 75. Но таких квадратов есть несколько, а именно: 64, 49, 36 и т. д. Докажем, что за 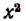надо брать наибольший из этих квадратов.

В самом деле, если бы мы взяли за 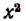, например, 49, то искомый корень содержал бы 7 десятков и несколько единиц и, будучи возведен в квадрат, дал бы число, меньшее 6400, т. е. меньшее точного квадрата, заключающегося в числе 7569.

Таким образом, число десятков искомого корня равно квадратному корню из наибольшего точного квадрата, заключающегося в числе сотен данного числа 7569.

Итак, х = 8. Теперь равенство

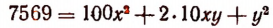
примет вид:

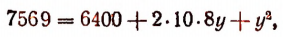
или

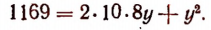
В левой части 116 десятков, а в правой либо 16у, либо больше, чем 16у. Поэтому

или

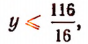
или

Значит, у равен или 7, или 6, или 5 и т. д.

Чтобы узнать настоящее значение у, придется последовательно испытать каждое из этих возможных значений, начиная с наибольшей цифры 7. В данном примере это испытание показывает, что надо взять у = 7. Действительно, выражение 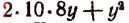при у = 7 оказывается в точности равным числу 1169.

Если бы значение выражения 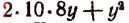при у = 7 оказалось больше, чем 1169, то следовало бы испытывать цифру 6 и т. д.

Итак,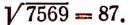

Правило. Чтобы извлечь квадратный корень из многозначного целого числа, разбивают его справа налево на грани по две цифры в каждой. В последней грани может оказаться либо одна, либо две цифры.

Чтобы найти первую цифру корня, извлекают квадратный корень из наибольшего точного квадрата, содержащегося в первой слева грани. Чтобы найти вторую цифру корня, из первой грани вычитают квадрат первой цифры корня и к остатку приписывают следующую грань. После этого число десятков получившегося остатка делят на удвоенную первую цифру корня; полученное целое кисло подвергают испытанию.
Следующие цифры корня находят по такому же приему.

Пример:

Найти

1-й шаг. Число, стоящее под знаком корня, разбиваем на грани по две цифры справа налево:

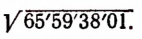
2-й шаг. Извлекаем квадратный корень из наибольшего точного квадрата, содержащегося в первой грани слева.

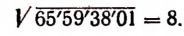
3-й шаг.

(Число 159 назовем первым остатком

4-й шаг.

Число 16 есть удвоенная найденная цифра 8)

5-й шаг. Делим число десятков первого остатка на 16. Получаем в целой части нуль. Эту цифру нуль приписываем к числу 16 и умножаем 160 на нуль. Найденную цифру нуль записываем также справа рядом с цифрой 8.

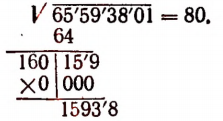
(Число 15 938 назовем вторым остатком).

6-й шаг. Делим число десятков второго остатка на 160, т.е. на удвоенное найденное уже число 80. Получаем в целой части цифру 9. Эту цифру 9 записываем справа рядом с цифрами 8 и 0.

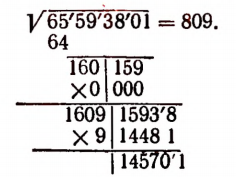
7-й шаг.

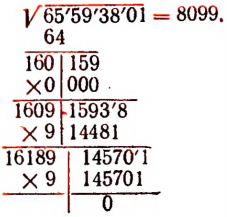
Пример:

Пример:

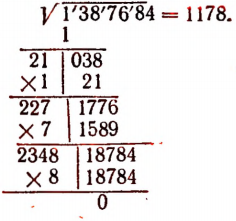
Извлечение квадратного корня с точностью до 1 из многозначных чисел, не являющихся точными квадратами

Эту операцию поясним на примерах.

Пример:

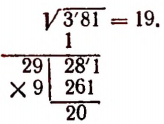
Очевидно, что 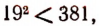а 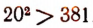. Поэтому число 19 есть приближенное значение с точностью до 1 с недостатком, а 20 — с избытком. Очевидно, что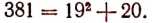

Пример:

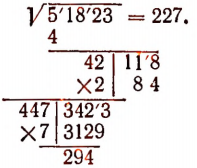
Число 224 есть приближенное значение с точностью до 1 с недостатком, а 245 — с избытком, так как

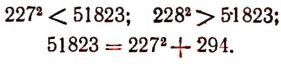
Извлечение квадратного корня из целых чисел с произвольно заданной точностью

Эту операцию поясним опять же на примерах.

1) Найти приближенное значение 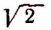с точностью до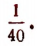

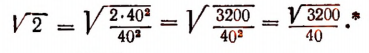
Найдем сначала 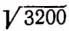с точностью до 1.

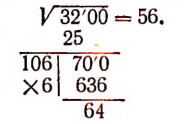
Легко понять, что значение 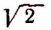с точностью до 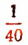будет с недостатком 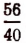, а с избытком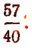

2) Найти приближенное значение 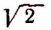с точностью до .

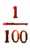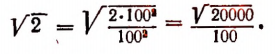
Найдем сначала с точностью до единицы:

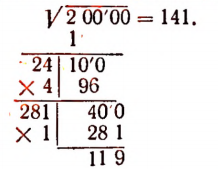
Значение 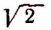с точностью до 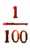будет с недостатком 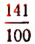, а с избытком .

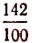При извлечении квадратного корня с точностью до 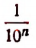вычисления можно располагать так:

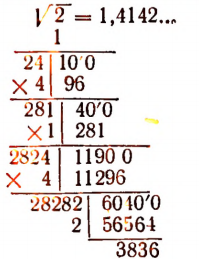
Здесь каждый раз мы приписывали к остатку два нуля. Иначе говоря, мы предварительно представляли 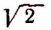в форме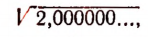

где после запятой поставлено четное число нулей.

Если в десятичной дроби после запятой имеется нечетное число десятичных знаков, то следует приписать еще один десятичный знак, равный нулю, и лишь после этого разбивать подкоренное число на грани.

Примеры:

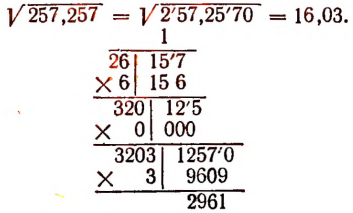
16,03 есть приближенное значение о недостатком о точностью до 0,01.

16,04 будет приближенным значением с избытком с той же точностью.

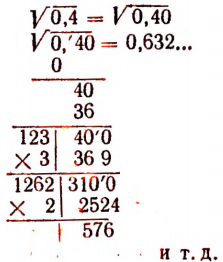
Пользуясь правилами извлечения квадратного корня, можно установить, например, что

Теорема о квадратном корне из двух

Теорема:

Среди целых и дробных чисел не существует такого числа, которое равнялось бы точно .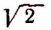

Эту теорему можно сформулировать и так: среди целых и дробных чисел нет такого числа, квадрат которого равнялся бы точно двум.

Доказательство:

Сначала докажем, что среди целых чисел не существует такого числа, квадрат которого равен 2. Квадрат единицы есть единица; квадрат двух — четыре; квадраты последующих целых чисел будут числами, еще большими, чем четыре. Поэтому нет такого целого числа, квадрат которого был бы равен 2:

Теперь докажем, что среди дробей также нет такой дроби, квадрат которой был бы равен 2.

Предположим противное тому, что требуется доказать, т. е. предположим, что существует дробное число 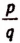, квадрат которого равен 2. Мы можем считать дробь 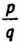несократимой, так как в виде несократимой дроби можно представить всякое дробное число.

Итак, допустим, что

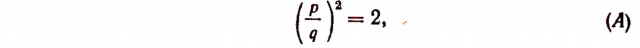
где р и q — целые взаимно простые* числа. Но тогда из равенства (А) получим, что . Из последнего равенства следует, что р есть четное число. (Если бы р было нечетным, то 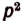было бы также нечетным, а потому равенство не могло иметь места.) Но всякое четное число можно представить в виде произведения, в котором один множитель равен двум, а другой — целому числу. Поэтому 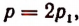где 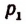—целое. 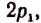Подставляя в равенство вместо р выражение получим , или 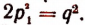Отсюда следует, что и q есть четное число.

Итак, оказалось, что числа р и q оба четные, что противоречит несократимости дроби .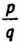

Таким образом, предположение, что существует дробное число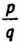, квадрат которого равен 2, привело нас к противоречию. Следовательно, такой дроби не существует, что и требовалось доказать.

Замечание:

Аналогично можно доказать, что среди целых и дробных чисел не существует и таких, квадраты которых были бы равны, например 3; 5; 6; 7; 8; 10; 11; 12; 13; 14; 15; 17;…

Ниже мы убедимся в существовании прямолинейных отрезков, отношение длин которых также не выражается ни целым, ни дробным числом, подобно тому как не выражается целым, или дробным числом, например, .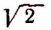

Несоизмеримые отрезки

Общей мерой двух отрезков называется такой отрезок, который укладывается в каждом из данных точно целое число раз.

Например, если отрезок MN (рис. 61) укладывается точно в отрезке АВ р раз, а в отрезке CD q раз, где р и q — целые числа, то отрезок MN будет общей мерой отрезков АВ и CD.

Если два отрезка имеют общую меру, то ах отношение выражается отношением целых чисел.

В предыдущем примере

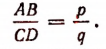
Обратное утверждение тоже справедливо, а именно:

если отношение двух отрезков равно отношению целых чисел, то эти отрезки имеют общую меру.

Пусть, например,

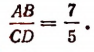
Тогда 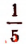часть отрезка CD будет их общей мерой.

На первый взгляд может показаться, что любые два отрезка имеют ту или иную общую меру. Однако в действительности это не так. Ниже, в следующем параграфе, мы докажем существование отрезков, не имеющих общей меры.

Отрезки, имеющие общую меру, называются соизмеримыми.

Отрезки же, не имеющие общей меры, называются несоизмеримыми.

Теорема о существовании несоизмеримых отрезков

Теорема:

Диагональ и сторона квадрата несоизмеримы.

Доказательство. Допустим противное, т. е. допустим, что диагональ и сторона квадрата соизмеримы. Тогда будет существовать некоторая общая мера этих отрезков.

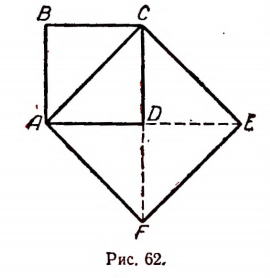
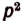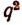Пусть эта общая мера укладывается на диагонали АС квадрата ABCD р раз, а на стороне АВ q раз. Если эту общую меру принять за единицу длины, то длины диагонали и стороны квадрата выразятся просто целыми числами р и q , а построенные на них квадраты (рис. 62) будут иметь площади, соответственно равные и (квадратных единиц).

На этом рисунке фигура ABCD есть квадрат, построенный на стороне АВ, а квадрат ACEF есть квадрат, построенный на диагонали АС.

Но, как видно из рисунка 62, квадрат ACEF, построенный на диагонали, вдвое больше данного квадрата ABCD (по площади), ибо состоит из четырех таких треугольников, каких данный квадрат содержит два.

Следовательно,

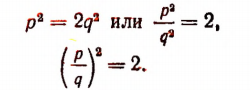
Но, как мы видели раньше (см. стр. 244), это невозможно. Значит, диагональ и сторона квадрата несоизмеримы.

Таким образом, мы доказали существование таких отрезков, точное отношение которых не выражается ни целым, ни дробным числом, т. е. доказали существование несоизмеримых отрезков.

О длине отрезка, несоизмеримого с отрезком, принятым за единицу длины

Пусть отрезки АВ и CD (рис. 63) несоизмеримы.

Примем длину отрезка CD за единицу длины. Тогда по доказанному в предыдущем параграфе длину АВ нельзя выразить никаким ни целым, ни дробным числом, если мы хотим, чтобы это выражение было бы абсолютно точным.

Теперь покажем процесс, с помощью которого можно находить длину АВ приближенно.

Первый шаг. На отрезке А В откладываем последовательно от точки А отрезок CD (рис. 64).

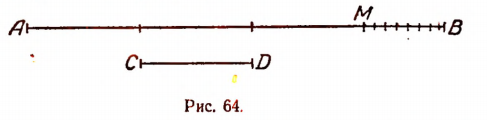
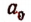Пусть оказалось, что отрезок CD уложился на АВ раз, где целое число (на рис. 64 = 3), и образовался остаток MB (разумеется меньший, чем CD). Такой остаток обязательно будет, так как в противном случае отрезки АВ и CD были бы соизмеримыми.

Второй шаг. На отрезке MB отложим последовательно 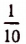часть CD от точки М. Пусть 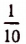часть CD уложилась на отрезке MB 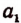раз (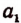 — целое число) и образовался остаток 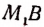(на рис. 64 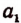= 7). Разумеется, остаток 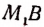будет меньше 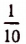CD.

Остаток 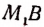опять же обязательно будет получаться в силу несоизмеримости отрезков АВ и CD.

Третий шаг. На новом остатке 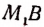станем откладывать 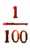отрезка CD. Получим целое число 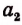и новый остаток.

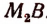(Точка 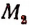на рис. 74 не указана.)

Этот процесс мы продолжаем дальше, делая четвёртый, пятый и дальнейшие шаги.

В силу несоизмеримости отрезков АВ и CD этот процесс теоретически никогда пе закончится и развернет перед нами бесконечный символ

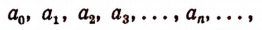
состоящий из бесконечного множества цифр, поставленных рядом друг с другом, который можно записать и так:

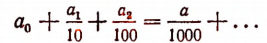
Обрывая наш измерительный процесс, скажем, на пятом шаге, мы получим десятичную дробь

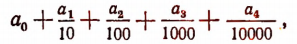
которая будет выражать длину АВ приближенно с недостатком с точностью до .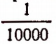

Десятичная дробь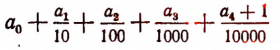

будет выражать длину АВ приближенно с избытком с точностью до .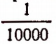

Обратим внимание на два факта, которые мы установили в этой главе.

1. Не существует ни целого, ни дробного числа, квадрат которого оказался бы равным точно двум.

2.Не существует ни целого, ни дробного числа, которое выражало бы точно длину отрезка, несоизмеримого с единицей длины.

Решение заданий и задач по предметам:

• Математика
• Высшая математика
• Математический анализ
• Линейная алгебра

Дополнительные лекции по высшей математике:

1. Тождественные преобразования алгебраических выражений
2. Функции и графики
3. Преобразования графиков функций
4. Квадратная функция и её графики
5. Алгебраические неравенства
6. Неравенства
7. Неравенства с переменными
8. Прогрессии в математике
9. Арифметическая прогрессия
10. Геометрическая прогрессия
11. Показатели в математике
12. Логарифмы в математике
13. Исследование уравнений
14. Уравнения высших степеней
15. Уравнения высших степеней с одним неизвестным
16. Комплексные числа
17. Непрерывная дробь (цепная дробь)
18. Алгебраические уравнения
19. Неопределенные уравнения
20. Соединения
21. Бином Ньютона
22. Число е
23. Непрерывные дроби
24. Функция
25. Исследование функций
26. Предел
27. Интеграл
28. Двойной интеграл
29. Тройной интеграл
30. Интегрирование
31. Неопределённый интеграл
32. Определенный интеграл
33. Криволинейные интегралы
34. Поверхностные интегралы
35. Несобственные интегралы
36. Кратные интегралы
37. Интегралы, зависящие от параметра
38. Квадратный трехчлен
39. Производная
40. Применение производной к исследованию функций
41. Приложения производной
42. Дифференциал функции
43. Дифференцирование в математике
44. Формулы и правила дифференцирования
45. Дифференциальное исчисление
46. Дифференциальные уравнения
47. Дифференциальные уравнения первого порядка
48. Дифференциальные уравнения высших порядков
49. Дифференциальные уравнения в частных производных
50. Тригонометрические функции
51. Тригонометрические уравнения и неравенства
52. Показательная функция
53. Показательные уравнения
54. Обобщенная степень
55. Взаимно обратные функции
56. Логарифмическая функция
57. Уравнения и неравенства
58. Положительные и отрицательные числа
59. Алгебраические выражения
60. Иррациональные алгебраические выражения
61. Преобразование алгебраических выражений
62. Преобразование дробных алгебраических выражений
63. Разложение многочленов на множители
64. Многочлены от одного переменного
65. Алгебраические дроби
66. Пропорции
67. Уравнения
68. Системы уравнений
69. Системы уравнений высших степеней
70. Системы алгебраических уравнений
71. Системы линейных уравнений
72. Системы дифференциальных уравнений
73. Квадратные и кубические корни
74. Извлечение квадратного корня
75. Рациональные числа
76. Иррациональные числа
77. Арифметический корень
78. Квадратные уравнения
79. Иррациональные уравнения
80. Последовательность
81. Ряды сходящиеся и расходящиеся
82. Тригонометрические функции произвольного угла
83. Тригонометрические формулы
84. Обратные тригонометрические функции
85. Теорема Безу
86. Математическая индукция
87. Показатель степени
88. Показательные функции и логарифмы
89. Множество
90. Множество действительных чисел
91. Числовые множества
92. Преобразование рациональных выражений
93. Преобразование иррациональных выражений
94. Геометрия
95. Действительные числа
96. Степени и корни
97. Степень с рациональным показателем
98. Тригонометрические функции угла
99. Тригонометрические функции числового аргумента
100. Тригонометрические выражения и их преобразования
101. Преобразование тригонометрических выражений
102. Комбинаторика
103. Вычислительная математика
104. Прямая линия на плоскости и ее уравнения
105. Прямая и плоскость
106. Линии и уравнения
107. Прямая линия
108. Уравнения прямой и плоскости в пространстве
109. Кривые второго порядка
110. Кривые и поверхности второго порядка
111. Числовые ряды
112. Степенные ряды
113. Ряды Фурье
114. Преобразование Фурье
115. Функциональные ряды
116. Функции многих переменных
117. Метод координат
118. Гармонический анализ
119. Вещественные числа
120. Предел последовательности
121. Аналитическая геометрия
122. Аналитическая геометрия на плоскости
123. Аналитическая геометрия в пространстве
124. Функции одной переменной
125. Высшая алгебра
126. Векторная алгебра
127. Векторный анализ
128. Векторы
129. Скалярное произведение векторов
130. Векторное произведение векторов
131. Смешанное произведение векторов
132. Операции над векторами
133. Непрерывность функций
134. Предел и непрерывность функций нескольких переменных
135. Предел и непрерывность функции одной переменной
136. Производные и дифференциалы функции одной переменной
137. Частные производные и дифференцируемость функций нескольких переменных
138. Дифференциальное исчисление функции одной переменной
139. Матрицы
140. Линейные и евклидовы пространства
141. Линейные отображения
142. Дифференциальные теоремы о среднем
143. Теория устойчивости дифференциальных уравнений
144. Функции комплексного переменного
145. Преобразование Лапласа
146. Теории поля
147. Операционное исчисление
148. Системы координат
149. Рациональная функция
150. Интегральное исчисление
151. Интегральное исчисление функций одной переменной
152. Дифференциальное исчисление функций нескольких переменных
153. Отношение в математике
154. Математическая логика
155. Графы в математике
156. Линейные пространства
157. Первообразная и неопределенный интеграл
158. Линейная функция
159. Выпуклые множества точек
160. Система координат