Оглавление:
При изучении аналитической геометрии вы научитесь решать задачи векторной алгебры и использовать свойства линейных операций с геометрическими векторами, скалярного, векторного и смешанного произведений векторов для решения геометрических задач. Вы научитесь решать задачи аналитической геометрии, связанные с различными видами уравнений плоскости и прямой и их взаимным расположением.
Разложение вектора по базису
Постановка задачи. Найти разложение вектора 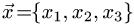
по векторам 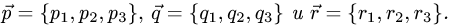
План решения.
1.Искомое разложение вектора 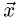 имеет вид
имеет вид
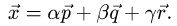
2.Это векторное уравнение относительно 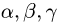 эквивалентно системе трех линейных уравнений с тремя неизвестными
эквивалентно системе трех линейных уравнений с тремя неизвестными
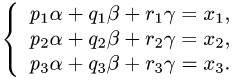
3.Peшaeм эту систему уравнений относительно 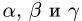 и таким
и таким
образом определяем коэффициенты разложения вектора  по векторам
по векторам 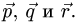 Записываем ответ в виде
Записываем ответ в виде 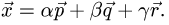
Замечание. Если система уравнений не имеет решений (векторы 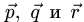 лежат в одной плоскости, а вектор
лежат в одной плоскости, а вектор 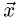 ей не принадлежит),
ей не принадлежит),
то вектор 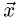 нельзя разложить по векторам
нельзя разложить по векторам 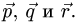 Если система
Если система
уравнений имеет бесчисленное множество решений (векторы 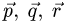 и вектор
и вектор 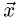 лежат в одной плоскости), то разложение вектора
лежат в одной плоскости), то разложение вектора 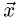 по векторам
по векторам 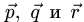 неоднозначно.
неоднозначно.
Пример:
Найти разложение вектора 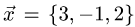 по векторам
по векторам
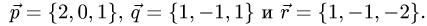
Решение:
1.Искомое разложение вектора 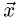 имеет вид
имеет вид
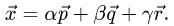
2.Это векторное уравнение относительно 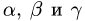 эквивалентно
эквивалентно
системе трех линейных уравнений с тремя неизвестными
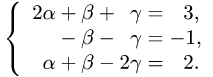
3.Система имеет единственное решение 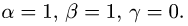
Ответ. 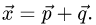
Коллинеарность векторов
Постановка задачи. Коллинеарны ли векторы 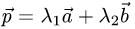 и
и
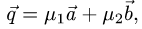 где
где 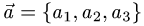 и
и 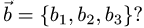
План решения. Векторы коллинеарны тогда и только тогда, когда существует число а такое, что 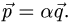 Иными словами, векторы коллинеарны тогда и только тогда, когда их координаты пропорциональны,
Иными словами, векторы коллинеарны тогда и только тогда, когда их координаты пропорциональны,
1.Находим координаты векторов 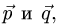 пользуясь тем, что при
пользуясь тем, что при
сложении векторов их координаты складываются, а при умножении
на число координаты умножаются на это число.
2.Если координаты векторов 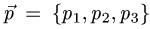 и
и 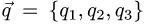 пропорциональны, т.е.
пропорциональны, т.е.
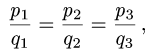
то векторы 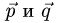 коллинеарны. Если равенства
коллинеарны. Если равенства
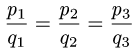
не выполняются, то векторы 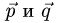 неколлинеарны.
неколлинеарны.
Пример:
Коллинеарны ли векторы 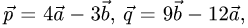 где
где
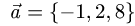 и
и 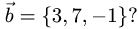
Решение:
1.Находим координаты векторов 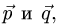 пользуясь тем, что при
пользуясь тем, что при
сложении векторов их координаты складываются, а при умножении
на число координаты умножаются на это число:
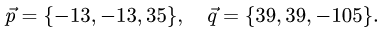
2.Так как
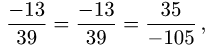
то координаты пропорциональны. Следовательно, векторы 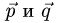 коллинеарны.
коллинеарны.
Ответ. Векторы 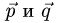 коллинеарны.
коллинеарны.
Угол между векторами
Постановка задачи. Даны точки 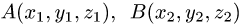 и
и
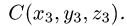 Найти косинус угла между векторами
Найти косинус угла между векторами 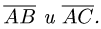
План решения. Косинус угла 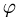 между векторами
между векторами 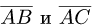 определяется формулой
определяется формулой
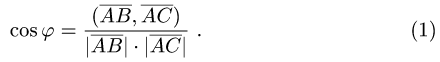
1.Чтобы вычислить длины векторов 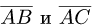 и скалярное
и скалярное
произведение 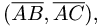 находим координаты векторов:
находим координаты векторов:
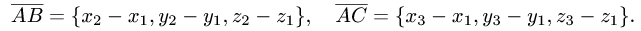
2.По формулам для длины вектора и скалярного произведения
векторов имеем
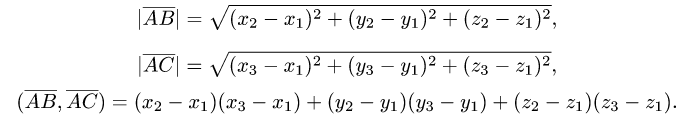
Вычисляем cos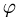 по формуле (1) и записываем ответ.
по формуле (1) и записываем ответ.
Пример:
Даны точки А(-2,4,-6), В(0,2,-4) и С(-6,8,-10).
Найти косинус угла между векторами 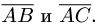
Решение:
1.Находим координаты векторов 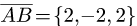 и
и 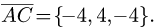
2.По формулам для длины вектора и скалярного произведения
векторов имеем
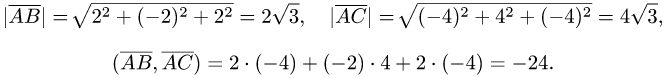
3.Вычисляем cos 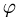 по формуле(1):
по формуле(1):
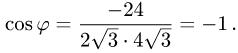
Ответ. Косинус угла между векторами 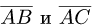 равен — 1.
равен — 1.
Площадь параллелограмма
Постановка задачи. Вычислить площадь параллелограмма, построенного на векторах 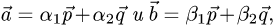 если известно,
если известно,
что 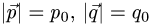 и угол между векторами
и угол между векторами 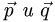 равен
равен 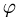 .
.
План решения. Площадь параллелограмма, построенного на векторах 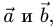 равна модулю их векторного произведения:
равна модулю их векторного произведения:

1.Вычисляем 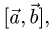 используя свойства векторного произведения
используя свойства векторного произведения

2.Вычисляем модуль векторного произведения
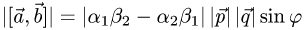
(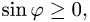 так как
так как 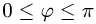 ).
).
3.Находим площадь параллелограмма, используя формулу(1)
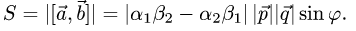
Пример:
Вычислить площадь параллелограмма, построенного на
векторах 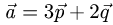 и
и 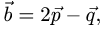 если известно, что
если известно, что 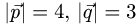 и угол между векторами
и угол между векторами 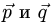 равен
равен 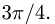
Решение:
1.Вычисляем 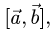 используя свойства векторного произведения
используя свойства векторного произведения
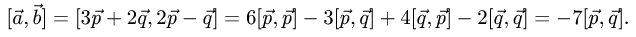
2.Вычисляем модуль векторного произведения
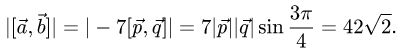
3.Находим площадь параллелограмма, используя формулу (1)
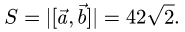
Ответ. Площадь параллелограмма равна 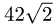 (ед. длины
(ед. длины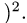
Компланарность векторов
Постановка задачи. Компланарны ли векторы 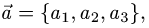
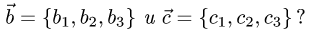
План решения. Для того чтобы три вектора были компланарны
(лежали в одной плоскости или в параллельных плоскостях), необходимо и достаточно, чтобы их смешанное произведение 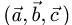 было равно нулю.
было равно нулю.
1.Смешанное произведение векторов выражается через их координаты формулой
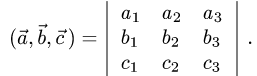
2.Если определитель в правой части этого равенства равен нулю,
то векторы компланарны, если определитель не равен нулю, то векторы некомпланарны.
Пример:
Компланарны ли векторы 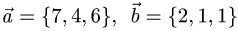 и
и 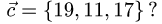
Решение:
1.Вычисляем смешанное произведение векторов:

2.Так как 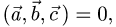 векторы
векторы 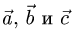 компланарны.
компланарны.
Ответ. Векторы 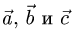 компланарны.
компланарны.
Объем и высота тетраэдра
Постановка задачи. Вычислить объем тетраэдра с вершинами в точках 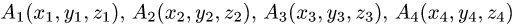 и его высоту, опущенную из вершины
и его высоту, опущенную из вершины 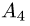 на грань
на грань 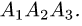
План решения.
1.Из вершины 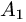 проведем векторы
проведем векторы 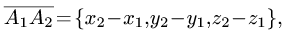
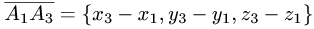 и
и 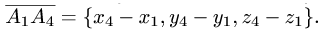
В соответствии с геометрическим смыслом смешанного произведения имеем
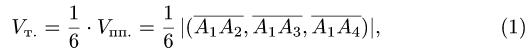
где 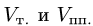 — объемы тетраэдра и параллелепипеда, построенных
— объемы тетраэдра и параллелепипеда, построенных
на векторах 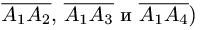
С другой стороны,
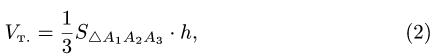
где согласно геометрическому смыслу векторного произведения
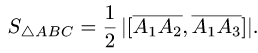
Сравнивая формулы (1) и (2), получаем
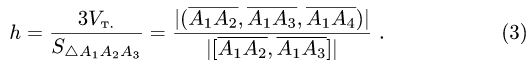
2. Вычисляем смешанное произведение
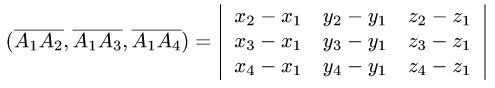
и находим объем тетраэдра по формуле (1).
3. Вычисляем координаты векторного произведения
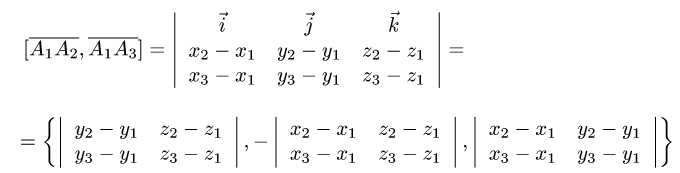
и его модуль.
4. Находим высоту h по формуле (3).
Пример:
Вычислить объем тетраэдра с вершинами 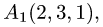
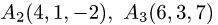 и
и 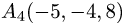 и его высоту, опущенную из
и его высоту, опущенную из
вершины 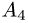 на грань
на грань 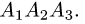
Решение:
1.Из вершины 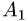 проведем векторы
проведем векторы 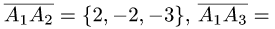
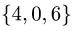 и
и 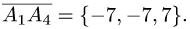
2.Вычисляем смешанное произведение:
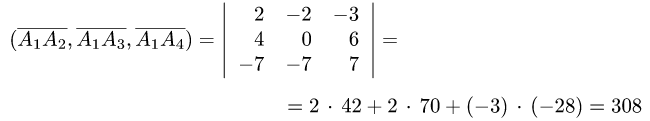
и находим объем тетраэдра по формуле (1) 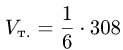 (ед.длины
(ед.длины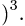
3.Вычисляем координаты векторного произведения:
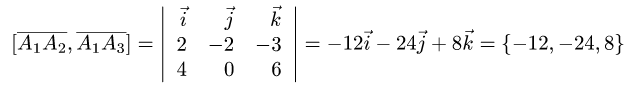
и его модуль
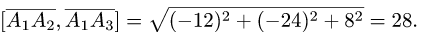
4.Находим высоту h по формуле (3):
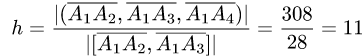 ед. длины.
ед. длины.
Ответ. 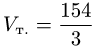 (ед.длины
(ед.длины h = 11 ед.длины.
h = 11 ед.длины.
Расстояние от точки до плоскости
Постановка задачи. Найти расстояние от точки 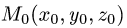
до плоскости, проходящей через точки 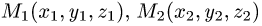 и
и 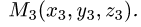
План решения. Искомое расстояние можно найти как высоту
тетраэдра с вершинами 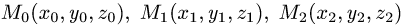 и
и
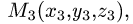 опущенную из вершины
опущенную из вершины 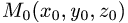 на грань
на грань 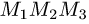 (см. задачу 1.6). Другое решение заключается в следующем.
(см. задачу 1.6). Другое решение заключается в следующем.
Расстояние d от точки 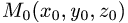 до плоскости равно длине
до плоскости равно длине
проекции вектора 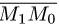 на нормальный вектор плоскости
на нормальный вектор плоскости 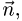 т.е.
т.е.
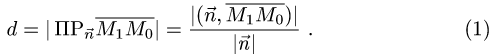
Поскольку нормальный вектор плоскости 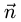 ортогонален векторам
ортогонален векторам
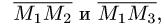 его можно найти как их векторное произведение:
его можно найти как их векторное произведение:
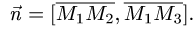
1.Находим координаты векторов:
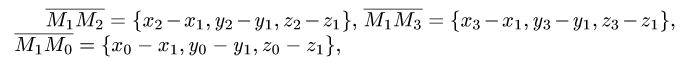
и нормального вектора плоскости:
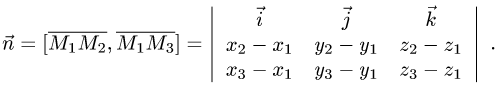
2.Вычисляем расстояние d от точки 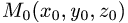 до плоскости
до плоскости
по формуле (1).
Пример:
Найти расстояние от точки 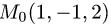 до плоскости,
до плоскости,
проходящей через точки 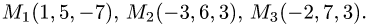
Решение:
1.Находим координаты векторов:
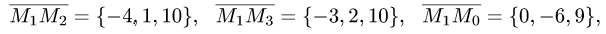
и нормального вектора плоскости:
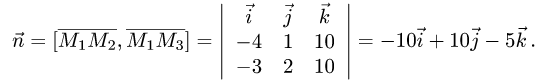
2.Вычисляем расстояние d от точки 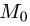 до плоскости по формуле (1):
до плоскости по формуле (1):
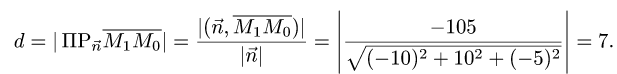
Ответ, d = 7 ед. длины.
Уравнение плоскости с данным нормальным вектором
Постановка задачи. Написать уравнение плоскости, проходящей через точку 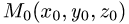 перпендикулярно вектору
перпендикулярно вектору 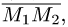 где точки
где точки 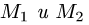 имеют координаты
имеют координаты 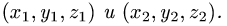
План решения. Уравнение плоскости, проходящей через точку
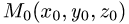 перпендикулярно вектору
перпендикулярно вектору 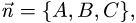 имеет вид
имеет вид
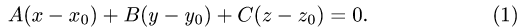
1.В качестве нормального вектора плоскости 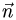 выбираем вектор
выбираем вектор 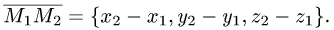
2.Составляем уравнение плоскости (1) с нормальным вектором
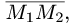 проходящей через точку
проходящей через точку 
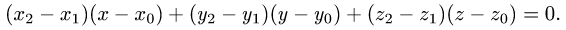
Пример:
Написать уравнение плоскости, проходящей через точку  перпендикулярно вектору
перпендикулярно вектору 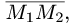 где точки
где точки  имеют координаты (7, 8,-1) и (9, 7, 4).
имеют координаты (7, 8,-1) и (9, 7, 4).
Решение:
1.В качестве нормального вектора плоскости 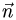 выбираем вектор
выбираем вектор
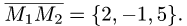
2.Составляем уравнение плоскости (1) с нормальным вектором
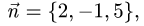 проходящей через точку
проходящей через точку 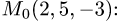
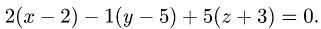
Ответ. Уравнение плоскости 2х — у + 5z + 16 = 0.
Угол между плоскостями
Постановка задачи. Найти угол между плоскостями
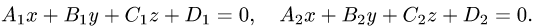
План решения. Двугранный угол между плоскостями равен углу
между их нормальными векторами
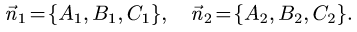
Поэтому угол  между плоскостями определяется равенством
между плоскостями определяется равенством
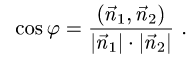
Пример:
Найти угол между плоскостями
х + 2y — 2z — 7 = 0, x + y — 35 = 0.
Решение:
Двугранный угол между плоскостями равен углу между их нормальными векторами 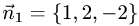 и
и 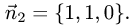 Поэтому угол
Поэтому угол 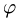 между плоскостями определяется равенством
между плоскостями определяется равенством
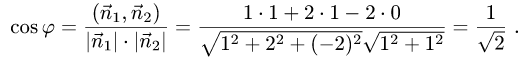
Таким образом, 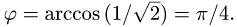
Ответ. Угол между плоскостями 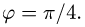
Канонические уравнения прямой
Постановка задачи. Написать канонические уравнения прямой, заданной как линия пересечения двух плоскостей (общими уравнениями)
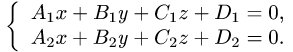
План решения.
1.Проверяем, что векторы 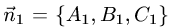 и
и 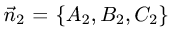
неколлинеарны и, следовательно, плоскости пересекаются по некоторой прямой.
Канонические уравнения прямой с направляющим вектором 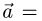
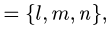 проходящей через данную точку
проходящей через данную точку 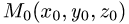 , имеют вид
, имеют вид
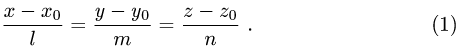
Поэтому чтобы написать уравнения прямой, необходимо найти ее направляющий вектор и какую-нибудь точку на прямой.
2.Так как прямая принадлежит одновременно обеим плоскостям,
то ее направляющий вектор 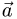 ортогонален нормальным векторам
ортогонален нормальным векторам
обеих плоскостей, т.е. 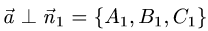 и
и 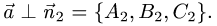
Следовательно, направляющий вектор 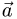 находим по формуле
находим по формуле
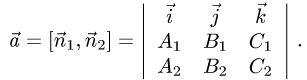
3.Теперь выберем какую-нибудь точку на прямой. Поскольку направляющий вектор прямой непараллелен хотя бы одной из координатных плоскостей, то прямая пересекает эту координатную плоскость. Следовательно, в качестве точки на прямой может быть взята точка ее пересечения с этой координатной плоскостью.
4.Подставляем найденные направляющий вектор и точку в уравнения прямой (1) и записываем ответ.
Пример:
Написать канонические уравнения прямой, заданной
как линия пересечения двух плоскостей (общими уравнениями)
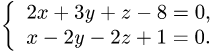
Решение:
1.Проверим, что векторы 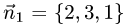 и
и 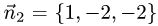 неколлинеарны (см. задачу 1.2). Имеем
неколлинеарны (см. задачу 1.2). Имеем
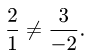
Векторы 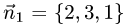 и
и 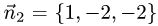 неколлинеарны, так как
неколлинеарны, так как
их координаты непропорциональны. Следовательно, две плоскости
пересекаются по прямой.
2.Так как прямая принадлежит одновременно обеим плоскостям,
то ее направляющий вектор 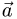 ортогонален нормальным векторам
ортогонален нормальным векторам
обеих плоскостей, т.е. 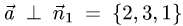 и
и 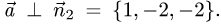
Следовательно, направляющий вектор 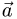 находим по формуле
находим по формуле
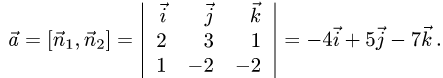
3.Теперь выберем какую-нибудь точку на прямой. Поскольку направляющий вектор прямой непараллелен ни одной из координатных плоскостей, то прямая пересекает все три координатные плоскости.
Следовательно, в качестве точки на прямой может быть взята точка ее пересечения, например, с плоскостью у = 0. Координаты этой
точки находим, решая систему трех уравнений
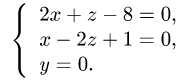
Получим 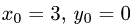 и
и 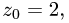 т.е.
т.е. 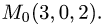
4.Подставляя найденные направляющий вектор и точку в уравнения прямой (1), получим
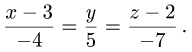
Ответ. Канонические уравнения прямой имеют вид
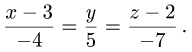
Точка пересечения прямой и плоскости
Постановка задачи. Найти точку пересечения прямой
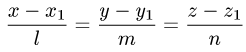
и плоскости
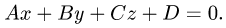
План решения.
1.Проверим, что прямая не параллельна плоскости. Это означает,
что направляющий вектор прямой 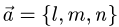 и нормальный вектор плоскости
и нормальный вектор плоскости 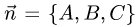 не ортогональны, т.е. их скалярное произведение не равно нулю:
не ортогональны, т.е. их скалярное произведение не равно нулю:
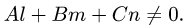
В этом случае существует единственная точка пересечения прямой и
плоскости.
2.Для нахождения точки пересечения прямой и плоскости, вообще
говоря, надо решить систему трех уравнений с тремя неизвестными
(два уравнения прямой и одно уравнение плоскости). Однако удобнее
использовать параметрические уравнения прямой.
Положим
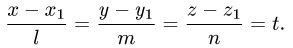
Тогда параметрические уравнения прямой имеют вид
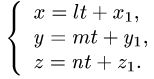
3.Подставляя эти выражения для x, у и z в уравнение плоскости
и решая его относительно t, находим значение параметра 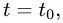 при котором происходит пересечение прямой и плоскости.
при котором происходит пересечение прямой и плоскости.
4.Найденное значение 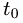 подставляем в параметрические уравнения прямой и получаем искомые координаты точки пересечения:
подставляем в параметрические уравнения прямой и получаем искомые координаты точки пересечения:
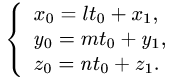
Записываем ответ в таком виде: прямая и плоскость пересекаются
в точке 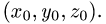
Пример:
Найти точку пересечения прямой
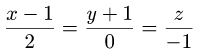
и плоскости
2x — 3y + z — 8 = 0.
Решение:
1.Имеем
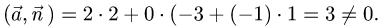
Следовательно, направляющий вектор прямой и нормальный вектор
плоскости не ортогональны, т.е. прямая и плоскость пересекаются в
единственной точке.
2.Положим
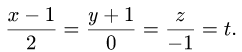
Тогда параметрические уравнения прямой имеют вид
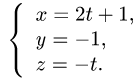
3.Подставляя эти выражения для x, у и z в уравнение плоскости,
находим значение параметра t, при котором происходит пересечение
прямой и плоскости:
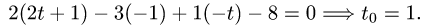
4.Подставляя в параметрические уравнения прямой найденное
значение 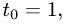 получаем
получаем
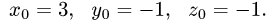
Ответ. Прямая и плоскость пересекаются в точке (3,-1,-1).
Проекция точки на плоскость или прямую
Постановка задачи. Найти координаты проекции 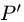 точки
точки 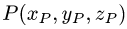 на плоскость Ах + By + Cz + D = 0.
на плоскость Ах + By + Cz + D = 0.
План решения. Проекция Р’ точки Р на плоскость является основанием перпендикуляра, опущенного из точки Р на эту плоскость.
1.Составляем уравнения прямой, проходящей через точку Р перпендикулярно данной плоскости. Для этого в качестве направляющего вектора прямой берем нормальный вектор плоскости:  {A,B,C}. Тогда канонические уравнения прямой имеют вид
{A,B,C}. Тогда канонические уравнения прямой имеют вид
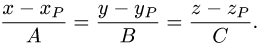
2.Находим координаты точки пересечения Р’ этой прямой с заданной плоскостью (см. задачу 1.11). Положим
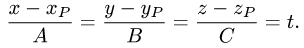
Тогда параметрические уравнения прямой имеют вид
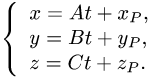
3.Подставляя x,y,z в уравнение плоскости и решая его относительно t, находим значение параметра 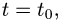 при котором происходит пересечение прямой и плоскости.
при котором происходит пересечение прямой и плоскости.
4.Найденное значение 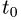 подставляем в параметрические уравнения прямой и получаем искомые координаты точки Р’.
подставляем в параметрические уравнения прямой и получаем искомые координаты точки Р’.
Замечание:
Аналогично решается задача о нахождении координат проекции точки на прямую.
Пример:
Найти координаты проекции Р’ точки Р(1,2, — 1) на
плоскость Зх — у +2z — 4 = 0.
Решение:
1.Составляем уравнения прямой, проходящей через точку Р перпендикулярно данной плоскости. Для этого в качестве направляющего вектора прямой берем нормальный вектор плоскости: 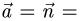 {3, — 1, 2}. Тогда канонические уравнения прямой имеют вид
{3, — 1, 2}. Тогда канонические уравнения прямой имеют вид
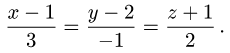
2.Найдем координаты точки пересечения Р’ этой прямой с задан-
заданной плоскостью. Положим
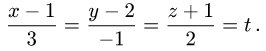
Тогда параметрические уравнения прямой имеют вид
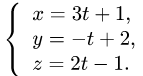
3.Подставляя эти выражения для х, у и z в уравнение плоскости,
находим значение параметра t, при котором происходит пересечение прямой и плоскости:
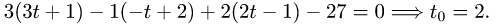
4.Подставляя в параметрические уравнения прямой найденное
значение 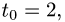 получаем
получаем 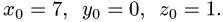
Таким образом, точка пересечения прямой и плоскости и, следовательно, проекция точки Р на плоскость имеет координаты (7, 0,1).
Ответ. Проекция Р’ имеет координаты (7,0,1).
Симметрия относительно прямой или плоскости
Постановка задачи. Найти координаты точки Q, симметричной точке 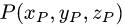 относительно прямой
относительно прямой
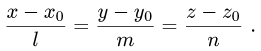
План решения. Искомая точка Q лежит на прямой, перпендикулярной данной и пересекающей ее в точке Р’. Поскольку точка
Р’ делит отрезок PQ пополам, координаты 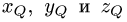 точки Q
точки Q
определяются из условий
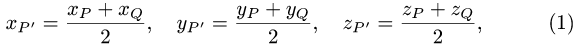
где 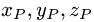 — координаты точки Р и
— координаты точки Р и 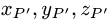 — координаты
— координаты
ее проекции Р’ на данную прямую.
1.Найдем проекцию точки Р на данную прямую, т.е. точку Р’
(см. задачу 1.12). Для этого:
а) составим уравнение плоскости, проходящей через точку Р перпендикулярно данной прямой. В качестве нормального вектора 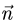 этой плоскости можно взять направляющий вектор данной прямой,
этой плоскости можно взять направляющий вектор данной прямой,
т.е. 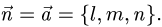 Получаем
Получаем
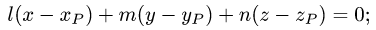
б) найдем координаты точки пересечения Р’ этой плоскости с заданной прямой. Для этого запишем уравнения прямой в параметрической форме
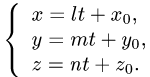
Подставляя х,у, z в уравнение плоскости и решая его относительно t,
находим значение параметра 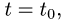 при котором происходит пересечение прямой и плоскости;
при котором происходит пересечение прямой и плоскости;
в) найденное значение 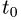 подставляем в параметрические уравнения прямой и получаем искомые координаты точки Р’.
подставляем в параметрические уравнения прямой и получаем искомые координаты точки Р’.
Координаты точки Q, симметричной точке Р относительно данной прямой, определяем из условий (1). Получаем
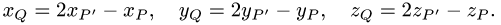
Замечание. Аналогично решается задача о нахождении координат точки, симметричной данной, относительно плоскости.
Пример:
Найти координаты точки Q, симметричной точке
Р(2, —1,2) относительно прямой
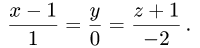
Решение:
1.Найдем проекцию точки Р на данную прямую, т.е. точку 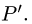 Для этого:
Для этого:
а) составим уравнение плоскости, проходящей через точку Р пер-
перпендикулярно данной прямой. В качестве нормального вектора 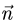 этой плоскости можно взять направляющий вектор данной прямой:
этой плоскости можно взять направляющий вектор данной прямой: 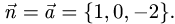 Тогда
Тогда
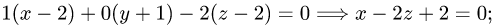
б) найдем точку пересечения заданной прямой и плоскости
x — 2z + 2 = 0. Для этого запишем уравнения прямой в параметрической форме:
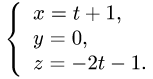
Подставляя эти выражения для х, у и z в уравнение плоскости, находим значение параметра t, при котором происходит пересечение
прямой и плоскости: 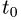 = — 1;
= — 1;
в) подставляя в параметрические уравнения прямой найденное
значение 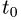 = — 1, получаем
= — 1, получаем
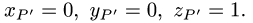
Таким образом, точка пересечения прямой и плоскости и, следовательно, проекция точки Р на прямую есть Р'(0, 0,1).
2.Координаты точки Q, симметричной точке Р относительно дан-
данной прямой, определяются из условий (1):
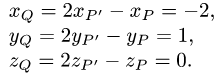
Геометрия на плоскости
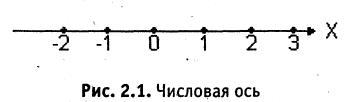
Прямая, для которой указано направление, начало отсчета и масштаб, называется числовой осью. Откладывая целое число единичных отрезков влево и вправо, получим изображение множества целых чисел (рис. 2.1). Если каждый из единичных отрезков оси разделить на n равных частей, то точки деления будут изображать дроби со знаменателем n, эти точки дают изображение всех рациональных чисел типа m/n. Можно доказать, что на любом сколь угодно малом интервале числовой оси всегда находятся рациональные точки. Этот факт выражается так: рациональные точки расположены на числовой оси всюду плотно.
Каждая пара точек m и n, вместе со всеми точками между ними, называется отрезком числовой оси (или сегментом) и обозначается [m, n]. Если же рассматриваются только промежуточные точки между m и n, то говорят о промежутке (или интервале) числовой оси (m, n). Расстояние от точки 0 до точки m есть положительное число, которое называется абсолютной величиной числа m, и обозначается |m|. Расстояние между точками m и n есть положительное число, которое называется длиной отрезка [m,n] и обозначается |m,n|. Пусть отрезок 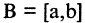 находится внутри отрезка
находится внутри отрезка 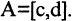 Если существуют такие два числа n и m, что длины отрезков А и В удовлетворяют соотношению
Если существуют такие два числа n и m, что длины отрезков А и В удовлетворяют соотношению 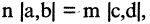 то говорят что отрезок и А и В соизмеримы.
то говорят что отрезок и А и В соизмеримы.
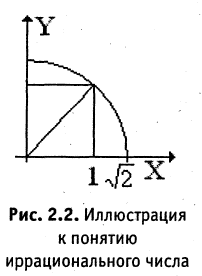
Возьмем квадрат со стороной, равной 1, его диагональ имеет длину 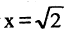 (рис. 2.2). Если бы
(рис. 2.2). Если бы 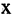 было соизмеримо с 1, то можно было бы найти такие два целых числа p и q, что
было соизмеримо с 1, то можно было бы найти такие два целых числа p и q, что 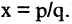 В этом случае
В этом случае 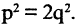 Можно доказать, что такого равенства быть не может. Вместе с тем при помощи циркуля на числовой оси от О можно отложить отрезок, равный диагонали квадрата. Построенная таким образом точка (правая граница отрезка
Можно доказать, что такого равенства быть не может. Вместе с тем при помощи циркуля на числовой оси от О можно отложить отрезок, равный диагонали квадрата. Построенная таким образом точка (правая граница отрезка 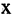 ) существует на числовой оси и не является рациональной. Такие точки, а, следовательно, и числа, не соизмеримые с единицей называются иррациональными. Все точки, лежащие на оси, образуют множество вещественных чисел.
) существует на числовой оси и не является рациональной. Такие точки, а, следовательно, и числа, не соизмеримые с единицей называются иррациональными. Все точки, лежащие на оси, образуют множество вещественных чисел.
Системы координат на плоскости
Прямоугольная (декартова) система координат на плоскости состоит из двух взаимно перпендикулярных числовых осей, пересекающихся в точке О, называемой началом системы координат. Горизонтальную ось называют осью абсцисс, а вертикальную — осью ординат. Каждой точке плоскости М можно сопоставить ориентированный отрезок ОМ, берущий начало в точке О и оканчивающийся в точке М (см. рис. 2.3). Такой отрезок называют радиус-вектором точки М. Числа 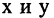 называются координатами точки М в декартовой системе координат. Положение любой точки плоскости М определяется заданием координат этой точки — упорядоченной пары чисел
называются координатами точки М в декартовой системе координат. Положение любой точки плоскости М определяется заданием координат этой точки — упорядоченной пары чисел 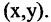 Задать точку в фиксированной системе координат означает указать значения ее координат. На плоскости расстояние d между двумя точками
Задать точку в фиксированной системе координат означает указать значения ее координат. На плоскости расстояние d между двумя точками 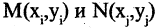 измеряется по прямой и вычисляется по формуле
измеряется по прямой и вычисляется по формуле
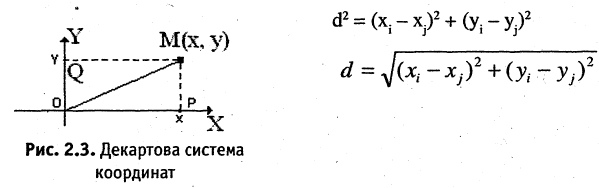
Пример:
Найти расстояние d между двумя точками М(-3,4) и N (5,2). Согласно вышеприведенной формуле, имеем
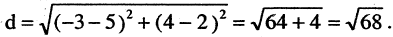
Прямая линия на плоскости
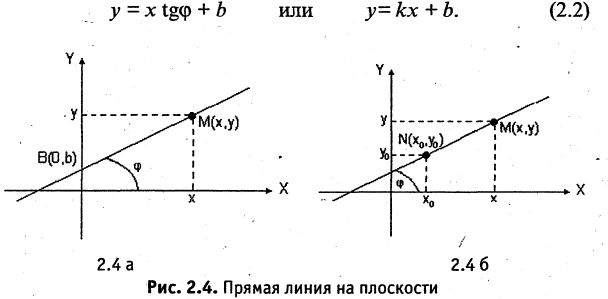
Пусть прямая линия пересекает ось ординат в точке  под углом
под углом  к оси абсцисс (см. рис. 2.4 а). Выберем на прямой произвольную точку
к оси абсцисс (см. рис. 2.4 а). Выберем на прямой произвольную точку 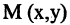 (такая точка называется текущей). Проекции направленного отрезка ВМ на оси координат соответственно равны
(такая точка называется текущей). Проекции направленного отрезка ВМ на оси координат соответственно равны 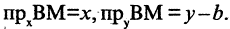 При скольжении точки М по прямой проекции изменяются, однако, их отношение, равное
При скольжении точки М по прямой проекции изменяются, однако, их отношение, равное
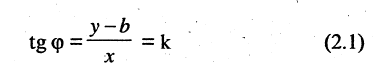
охраняется для всех точек прямой и не выполняется для точек, не принадлежащих прямой. Тангенс угла 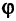 называется угловым коэффициентом и обозначается k. Выразив из (2.1) у, получим «уравнение прямой линии с угловым коэффициентом»
называется угловым коэффициентом и обозначается k. Выразив из (2.1) у, получим «уравнение прямой линии с угловым коэффициентом»
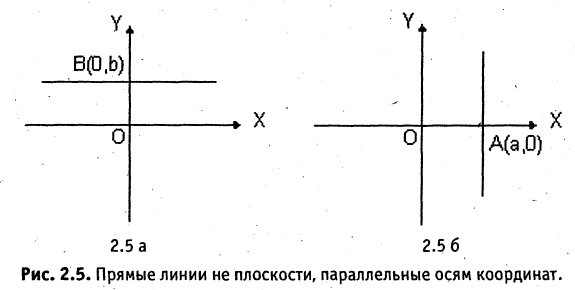
Если 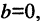 то прямая проходит через начало координат. Если
то прямая проходит через начало координат. Если 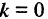 (см. рис. 2.5 а), то прямая проходит параллельно оси абсцисс и ее уравнение
(см. рис. 2.5 а), то прямая проходит параллельно оси абсцисс и ее уравнение 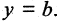 Если вместо точки В дана другая фиксированная точка
Если вместо точки В дана другая фиксированная точка 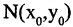 (см. рис. 2.5 б), то уравнение прямой, проходящей через данную точку
(см. рис. 2.5 б), то уравнение прямой, проходящей через данную точку
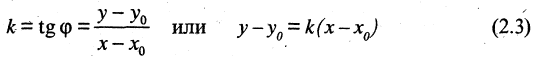
Любое из уравнений прямой можно привести к виду 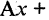
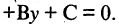 Например, для уравнения (2.2)
Например, для уравнения (2.2) 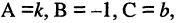 т. е. прямая в прямоугольной системе координат может быть описана линейным уравнением первой степени. Если
т. е. прямая в прямоугольной системе координат может быть описана линейным уравнением первой степени. Если 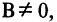 то и линейное уравнение можно привести к виду (2.2)
то и линейное уравнение можно привести к виду (2.2)
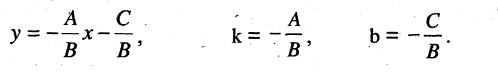
Если 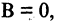 то получим уравнение
то получим уравнение 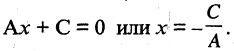 Это уравнение определяет прямую, параллельную оси ординат и пересекающую ось абсцисс в точке
Это уравнение определяет прямую, параллельную оси ординат и пересекающую ось абсцисс в точке 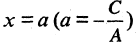 (рис. 2.5 б). Уравнение
(рис. 2.5 б). Уравнение 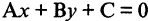 описывает только прямые линии на плоскости и называется общим уравнением прямой на плоскости. Верно и обратное утверждение: каждому уравнению первой степени с двумя неизвестными соответствует в прямоугольной системе координат одна и только одна прямая.
описывает только прямые линии на плоскости и называется общим уравнением прямой на плоскости. Верно и обратное утверждение: каждому уравнению первой степени с двумя неизвестными соответствует в прямоугольной системе координат одна и только одна прямая.
Кривые второго порядка
Кривыми второго порядка называются линии, которые описываются алгебраическими уравнениями второй степени
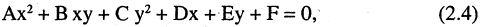
причем хотя бы один из коэффициентов А, В, С должен быть не равен нулю.
Окружностью называется геометрическое место точек, равноудаленных от данной точки, называемой центром окружности. Уравнение окружности радиуса R с центром в точке М(а, b) имеет вид
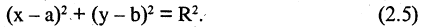
Если раскрыть скобки, то мы увидим, что уравнение (2.5) получается из уравнения (2.4), если 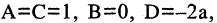
Пример:
Пусть задано уравнение 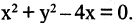 Является ли это уравнение уравнением окружности и, если да, то каков ее радиус и координаты центра? Попробуем привести данное уравнение к виду (2.5). Выделим полный квадрат относительно х, прибавляя и вычитая число 4.
Является ли это уравнение уравнением окружности и, если да, то каков ее радиус и координаты центра? Попробуем привести данное уравнение к виду (2.5). Выделим полный квадрат относительно х, прибавляя и вычитая число 4.
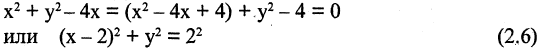
Сравнивая (2.6) с (2.5), видим, что заданное уравнение есть уравнение окружности радиусом 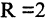 и с центром в точке М(2,0).
и с центром в точке М(2,0).
Эллипс — замкнутая кривая, для всех точек которой сумма расстояний до двух фиксированных точек 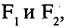 называемых фокусами эллипса, одинакова и равна, по определению,
называемых фокусами эллипса, одинакова и равна, по определению, 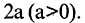 Для эллипса, представленного на рис. 2.6, сумма расстояний
Для эллипса, представленного на рис. 2.6, сумма расстояний 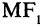 и
и 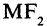 равна сумме расстояний
равна сумме расстояний 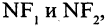 т. е.
т. е.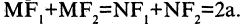
Уравнение эллипса, центр симметрии которого находится в начале координат, а фокусы 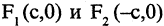 лежат на оси ОХ симметрично относительно оси ОY, называется каноническим
лежат на оси ОХ симметрично относительно оси ОY, называется каноническим
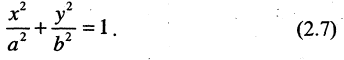
Параметры а и b называются полуосями, причем.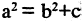 Уравнение (2.7) получим из (2.4), если
Уравнение (2.7) получим из (2.4), если 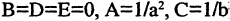
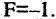 Очевидно, что окружность — частный случай эллипса, которого
Очевидно, что окружность — частный случай эллипса, которого 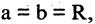 а центр находится в начале координат.
а центр находится в начале координат.
Гипербола — неограниченная кривая, для всех точек которой разность расстояний до двух фиксированных точек, называемых фокусами, есть величина постоянная и по определению равная 2а (рис. 2.7). Разность 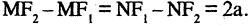 Канонической уравнение гиперболы, центр симметрии которой совпадает 4 началом координат, а фокусы
Канонической уравнение гиперболы, центр симметрии которой совпадает 4 началом координат, а фокусы 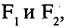 лежат на оси ОХ симметрично оси ОY,
лежат на оси ОХ симметрично оси ОY,

Параметры а и b называются полуосью и мнимой полуосью гиперболы, причем 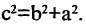 Уравнение (2.8) получим из (2.4), если
Уравнение (2.8) получим из (2.4), если 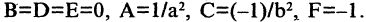 Особенность гиперболы — наличие асимптот — прямых, к которым неограниченно приближается кривая при
Особенность гиперболы — наличие асимптот — прямых, к которым неограниченно приближается кривая при 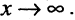 Уравнение асимптот:
Уравнение асимптот: 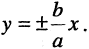
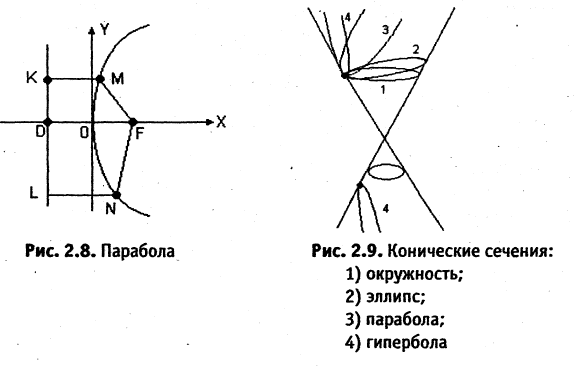
Парабола — неограниченная кривая, все точки которой (см. рис. 2.8) равноудалены от точки, называемой фокусом, и прямой, называемой директрисой, причем расстояние между фокусом и директрисой равно р. Для параболы, изображенной на рис. 2.8, расстояния 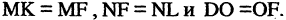 Каноническое уравнение параболы, фокус которой
Каноническое уравнение параболы, фокус которой 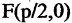 лежит на оси
лежит на оси
ОХ, а директриса 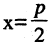
перпендикулярна ОХ, есть 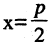

Уравнение (2.9) получим из (2.4), если 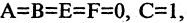
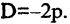 Ось такой параболы совпадает с осью ОХ, а вершина лежит в начале координат.
Ось такой параболы совпадает с осью ОХ, а вершина лежит в начале координат.
Сделав поворот и сдвиг системы координат, любое уравнение (2.4) можно привести только к одному из трех уравнений второй степени: (2.7), (2.8), (2.9) или к уравнению вида 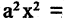
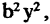 которому соответствуют две прямые. Это означает, что уравнениями второй степени можно описать только эллипс (и его частный случай — окружность), гиперболу или параболу. Важным свойством линий второго порядка является то, что все они могут быть получены (см. рис. 2.9) как сечения конуса плоскостью, пересекающей его под различными углами.
которому соответствуют две прямые. Это означает, что уравнениями второй степени можно описать только эллипс (и его частный случай — окружность), гиперболу или параболу. Важным свойством линий второго порядка является то, что все они могут быть получены (см. рис. 2.9) как сечения конуса плоскостью, пересекающей его под различными углами.
Преобразование системы координат
Пусть даны две системы прямоугольных координат 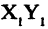 и
и 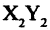 (рис. 2.10 а). Свяжем координаты точки
(рис. 2.10 а). Свяжем координаты точки 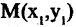 в одной
в одной
из систем с ее же координатами 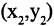 в другой системе координат. Решение задачи проводим в два этапа: вначале совмещаются начала координат, причем сохраняются старые направления осей (рис. 2.10 б), потом одна из систем поворачивается так, чтобы совпали направления осей координат.
в другой системе координат. Решение задачи проводим в два этапа: вначале совмещаются начала координат, причем сохраняются старые направления осей (рис. 2.10 б), потом одна из систем поворачивается так, чтобы совпали направления осей координат.
Параллельный перенос системы координат. В первой системе координат точка  имеет координаты (0,0), точка
имеет координаты (0,0), точка 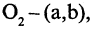 а точка
а точка 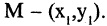 Рассматривая проекции этих точек на оси координат первой системы, имеем
Рассматривая проекции этих точек на оси координат первой системы, имеем
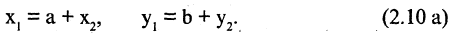
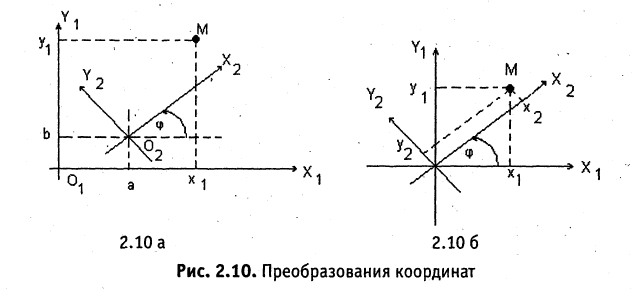
Чтобы получить координаты во второй системе, необходимо провести обратные действия. Это приведет к зависимостям
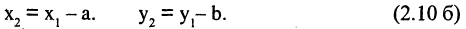
Поворот системы координат с совмещенной точкой начала. Пусть оси 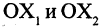 повернуты на угол
повернуты на угол 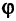 . Из рис. 2.10 б следуют соотношения
. Из рис. 2.10 б следуют соотношения
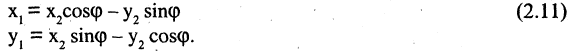
В общем случае связь между координатами точки в различных прямоугольных системах координат выражается линейными соотношениями

Пример:
Как изменятся координаты точки М(-2,3), если система будет повернута на 30° и сдвинута вверх на две единицы?
Применяя формулы (2.12) для 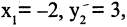 угла
угла 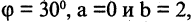 имеем
имеем
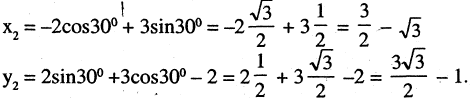
Для определения положения точек на плоскости часто применяется так называемая полярная система координат. Выберем на плоскости фиксированную точку О, называемую полюсом, и исходящую из нее ось ОР, называемую полярной осью. На полярной оси выбрана единица масштаба. В этой систем как показано на рис. 2.11, положение точки М на плоскость вполне задается отрезком ОМ, называемым полярным радиусом точки М, равным расстоянию отрезка ОМ, и углом 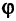 , который составляет полярный радиус с полярной осью, считая против часовой стрелки от полярной оси
, который составляет полярный радиус с полярной осью, считая против часовой стрелки от полярной оси 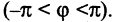
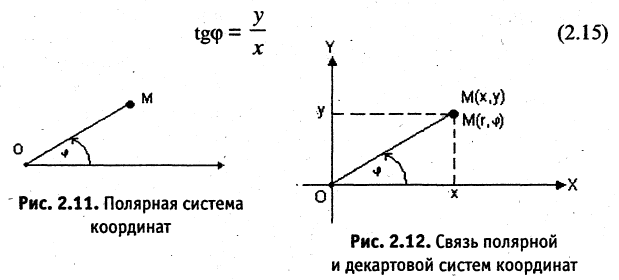
Если на плоскости заданы прямоугольная и полярная системы координат, причем начало координат и положительная часть оси абсцисс прямоугольной системы совпадают соответственно с полюсом и осью полярной системы координат (рис. 2.12), то декартовы и полярные координаты точки М связаны соотношением

Формулы (2.13) выражают координаты точки М в прямоугольной системе через ее же координаты в полярной системе. Отсюда
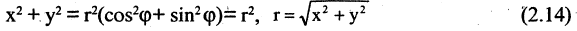
Геометрия в пространстве
Системы координат в пространстве:
Прямоугольная (декартова) система координат в пространстве возникает, если взяты три одинаковые взаимно перпендикулярные числовые оси — оси координат, которые пересекаются в точке О, называемой началом системы координат. Первую ось ОХ называют осью абсцисс, вторую ось ОY — осью ординат, третью ОХ — осью аппликат. Через каждые две (из трех) координатные оси проходит координатная плоскость.
Существуют две, не сводящиеся друг к другу системы координат: правая система координат и левая система координат. Различить эти системы координат можно следующим образом: если посмотреть из любой положительной точки оси ОZ на ось ОY и ось ОХ окажется справа, то это правая система координат, если слева — левая (сравните рис. 2.13 а и рис. 2.13 6).
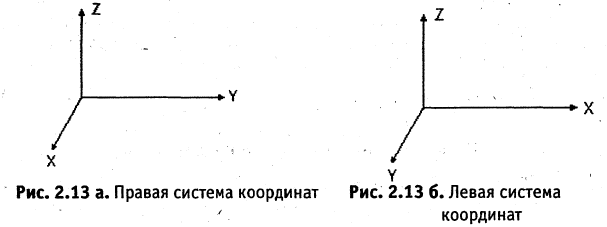
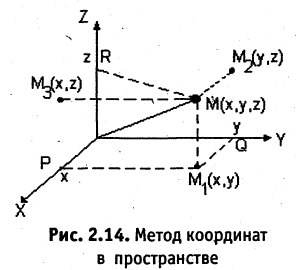
Каждой пространственной точке М можно сопоставить ориентированный отрезок ОМ, берущий начало в точке начала координат и оканчивающийся в точке М (см. рис. 2.14). Такой отрезок называют радиус-вектором точки М. Спроектируем точку М на оси координат. Каждой точке М соответствуют три точки на осях (на рис. 2.14 Р, Q, R) их координаты называют координатами точки М. Они однозначно определяют положение этой точки в выбранной системе координат. Наоборот, задав на каждой из осей координат по одной точке, например, Р, Q, и R, мы определим одну и только одну точку в пространстве (на рис. 2.14 точка М). Эта точка получается при пересечении трех взаимно перпендикулярных плоскостей 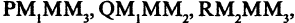 проходящих соответственно через точки Р, Q и R параллельно осям координат. Расстоянием между двумя точками
проходящих соответственно через точки Р, Q и R параллельно осям координат. Расстоянием между двумя точками 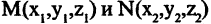 в пространстве называется число d, равное длине отрезка прямой, соединяющей эти точки
в пространстве называется число d, равное длине отрезка прямой, соединяющей эти точки
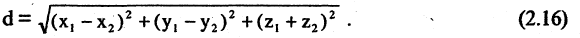
Например, расстояние между двумя точками М(2,-1,3) и N(-2,-1,0), согласно (2.16), равно
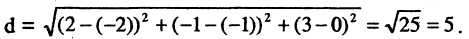
В пространстве всякая поверхность может рассматриваться как некоторое множество точек, между координатами которых установлены определенные соответствия

Основные поверхности в пространстве
- Плоскость в пространстве. Наиболее простой вид уравнения (2.17) — уравнение, линейное относительно всех неизвестных
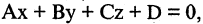 которое описывает плоскость в пространстве. Если
которое описывает плоскость в пространстве. Если 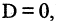 то уравнение
то уравнение 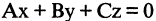 описывает плоскость, проходящую через начало координат (см. главу 2.4).
описывает плоскость, проходящую через начало координат (см. главу 2.4).
2. Цилиндрические поверхности — это поверхности, описываемые прямой, называемой образующей, двигающейся параллельно фиксированной заданной прямой и пересекающей некоторую линию L, называемую направляющей цилиндрической поверхности. Направляющая линия не обязательно замкнута. В частности, если образующая параллельна оси ОZ, то уравнение такой цилиндрической поверхности описывается уравнением, не содержащим z
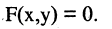
В этом случае вид функции F определяет направляющую линию цилиндра. Так, (см. рис. 2.5 а, б, в)) в пространстве
уравнение 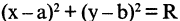 описывает круговой цилиндр,
описывает круговой цилиндр,
уравнение 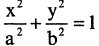 описывает эллиптический цилиндр,
описывает эллиптический цилиндр,
уравнение 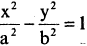 описывает гиперболический цилиндр.
описывает гиперболический цилиндр.
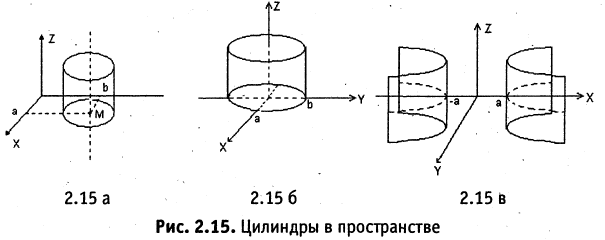
Пример:
Какую поверхность определяет следующее уравнение: 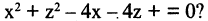
Решение. Выделим полные квадраты в левой части уравнения: 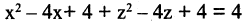 или
или 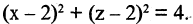 Это уравнение описывает круговой цилиндр, вытянутый вдоль оси ОY (координата у отсутствует).
Это уравнение описывает круговой цилиндр, вытянутый вдоль оси ОY (координата у отсутствует).
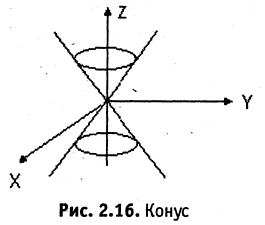
3. Конические поверхности. Поверхность, описываемая прямой (образующая конической поверхности), проходящей через данную точку, называемую вершиной, и пересекающей данную линию (направляющую конуса), называется конической поверхностью.
Наиболее простой формулой описывается конус, имеющий вершину в начале координат, а его образующая описывает вокруг оси координат некоторую замкнутую кривую, например, как показано на рис. 2.16, эллипс. Уравнение такого конуса имеет вид
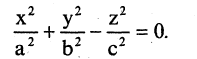
Пример:
Найти уравнение поверхности, возникающей при вращении прямой 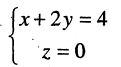 вокруг оси OX.
вокруг оси OX.
Решение. При вращении прямой возникнет коническая поверхность. Вершиной конуса будет являться точка пересечения его образующей с осью ОХ с координатами 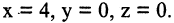 Произвольная фиксированная точка образующей прямой
Произвольная фиксированная точка образующей прямой 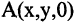 при вращении вокруг оси ОХ описывает окружность, задаваемую уравнением
при вращении вокруг оси ОХ описывает окружность, задаваемую уравнением 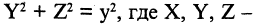 произвольные точки поверхности искомого конуса, соответствующие сечению
произвольные точки поверхности искомого конуса, соответствующие сечению 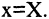 Подставляя значения
Подставляя значения 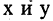 в уравнение образующей прямой, имеем искомое уравнение конуса
в уравнение образующей прямой, имеем искомое уравнение конуса 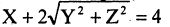 или, после преобразования,
или, после преобразования, 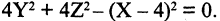
4. Сфера есть геометрическое место точек в пространстве, равноудаленных от одной точки, называемой центром. Величина удаления точек сферы от центра есть расстояние от точки центра до точек сферы.
Следовательно, используя (2.16), можно записать уравнение сферы
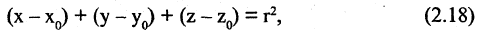
где r — радиус сферы или расстояние от произвольной точки сферы 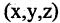 до ее центра — фиксированной точки с координатами
до ее центра — фиксированной точки с координатами 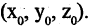
5. Поверхности вращения. Пусть в плоскости YОZ лежит кривая, уравнение которой 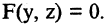 Если вращать эту кривую вокруг оси ОZ, то образуется поверхность вращения, описываемая уравнением
Если вращать эту кривую вокруг оси ОZ, то образуется поверхность вращения, описываемая уравнением

При анализе поверхностей вращения в каждом конкретном случае необходимо указывать, в какой плоскости лежит образующая кривая и вокруг какой оси она вращается. Так, например, эллипсоид вращения, описываемый уравнением
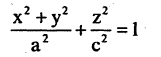
образован вращением вокруг оси ОZ эллипса, лежащего в плоскости ХОZ (рис. 2.17 а). Если этот же эллипс вращать вокруг оси ОХ, то уравнение соответствующего эллипсоида вращения (рис. 2.17 б) имеет вид
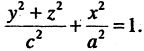
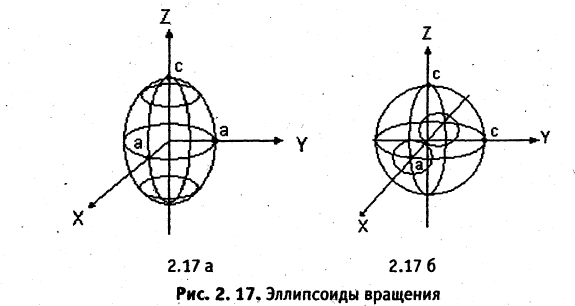
Пример:
Записать уравнение эллипсоида вращения, полученного от вращения эллипса вокруг оси ОY, если на его поверхности лежат точки А(3,0,0) и В(0,2,0).
Решение:
Заданные точки лежат в координатной плоскости ХОY и определяют вершины эллипса 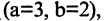 вращение которого образует искомый эллипсоид. Принимая во внимание предыдущие рассуждения, запишем уравнение эллипсоида вращения
вращение которого образует искомый эллипсоид. Принимая во внимание предыдущие рассуждения, запишем уравнение эллипсоида вращения
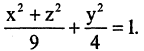
Линию в пространстве образует пересечение двух поверхностей. Отсюда следует, что пространственную линию можно описать системой двух уравнений
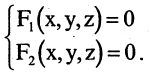
Пример:
Найти линию, образуемую пересечением плоскости 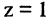 со сферой
со сферой 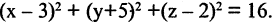
Решение:
Искомая линия находится как решение системы этих уравнений
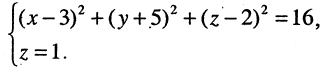
Решение этой системы есть уравнение окружности 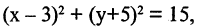 т. е. плоскость пересекает сферу по окружности.
т. е. плоскость пересекает сферу по окружности.
Пересечение трех поверхностей может давать просто точку в пространстве. Математически это соответствует единственному решению системы трех уравнений

Если система (2.20) несовместна, то это означает, что поверхности, описываемые данными уравнениями, не пересекаются в одной точке.
Основы аналитической геометрии
Направленные отрезки
Положение точки на прямой линии определяется одной координатой.
Одно из двух взаимных направлений данной прямой (безразлично какое) называется положительным и обозначается стрелкой.
Противоположное направление называется отрицательным (рис. 3.1).

За начало координат принимают точку О (ноль). Прямую обычно
называют какой-либо буквой, например X. За единицу масштаба
принимают какой-либо отрезок прямой, например ОЕ = 1. Координатой точки М, лежащей на прямой, является длина отрезка ОМ со знаком «плюс», если точка М удалена в положительном направлении от точки О, и со знаком «минус», если точка М удалена в
отрицательном направлении от точки О, т.е. координату точки М можно представить в виде
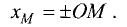
Пример:
Обозначить на координатной оси ОХ точки,
имеющие координаты: 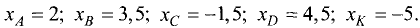
Решение:
Выбираем масштаб, имеющий длину 
Точки с указанными координатами представлены на рис. 3.2. ►

Направленный отрезок характеризуется длиной и направлением
(рис. 3.3). Отрезок начинается в точке А и заканчивается в точке
В. Обозначается 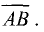

Направленные отрезки 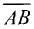 и
и 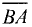 равны по длине
равны по длине 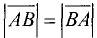 и
и
противоположны по направлению.
Если известны координаты начала 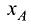 и конца
и конца 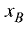 отрезка, то
отрезка, то
его длина рассчитывается по формуле
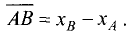
Пример:
Найти длину отрезка с координатами начала и
конца, представленными в табл. 3.1.
Таблица 3.1

Решение:
Результаты расчета представлены в табл. 3.2.
Таблица 3.2
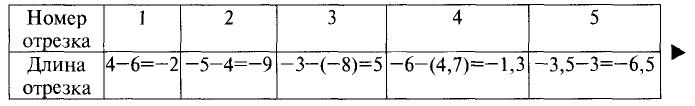
Знак «минус» перед значением длины отрезка указывает на
направление отрезка, противоположное направлению оси.
Прямоугольная система координат
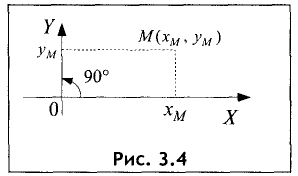
Положение точки на поверхности (плоскость, поверхность шара
и т. д.) определяется двумя координатами (рис. 3.4).
Прямоугольная система координат на плоскости представляет из
себя две перпендикулярные прямые, снабженные масштабами и
направлениями. Такие прямые называются координатными осями.
Координатами точки называются координаты оснований
перпендикуляров, опущенных из этой точки на координатные оси (рис. 3.4).
Ось ОХ называется осью абсцисс, а ось OY — осью ординат.
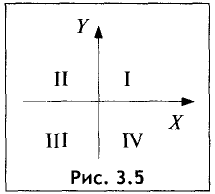
Четыре угла, образуемые осями координат, называются координатными углами и обозначаются I, II, III, IV (рис. 3.5).
Если не требовать перпендикулярности осей координат, то получим более общую систему декартовых координат.
Прямоугольная система координат является частным случаем декартовой.
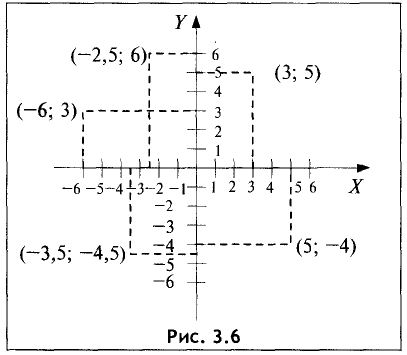
Пример:
Построить на плоскости в прямоугольной системе координат точки, имеющие следующие координаты: (3; 5), (—2,5; 6),
(5; -4), (-3,5; -4,5), (-6; 3).
Решение:
Указанные точки представлены на
рис. 3.6. ►
Расстояние 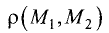 между двумя точками
между двумя точками 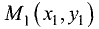 и
и 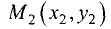 на плоскости определяется выражением
на плоскости определяется выражением
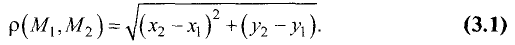
Действительно, проведем через каждую из точек  и
и  по паре прямых, параллельных координатным осям (рис. 3.7).
по паре прямых, параллельных координатным осям (рис. 3.7).
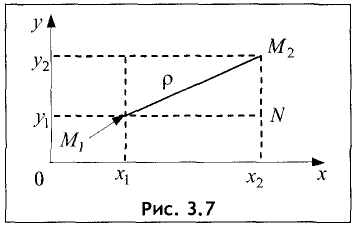
Отсюда следует, что треугольник 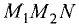 — прямоугольный с катетами
— прямоугольный с катетами 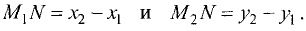
Поэтому гипотенуза равна
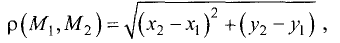
что и требовалось доказать.
Пример:
Найти периметр треугольника ABC по следующим
данным: А(2; 7), В(5; 7), С(5; 11).
Решение:
Исследуемый треугольник
представлен на рис. 3.8.
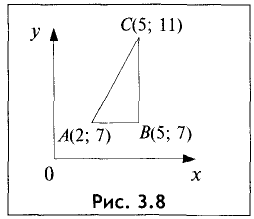
Прямая АВ равноудалена от оси Ох, поэтому она параллельна этой оси. По этой же причине прямая ВС параллельна оси Оу. Поэтому АВ и ВС перпендикулярны, т.е. треугольник ABC — прямоугольный. Таким образом, АВ= 5 — 2 = 3, ВС= 11 -7 = 4, 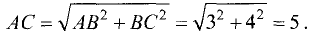
Периметр треугольника П=3 + 4 + 5= 12. ►
Деление отрезка в данном отношении
Даны точки 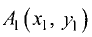 и
и 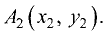 Найти точку М(х, у) (ее координаты), делящую отрезок
Найти точку М(х, у) (ее координаты), делящую отрезок 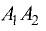 в отношении
в отношении 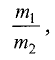 т.е.
т.е. 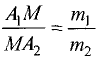 (рис. 3.9).
(рис. 3.9).
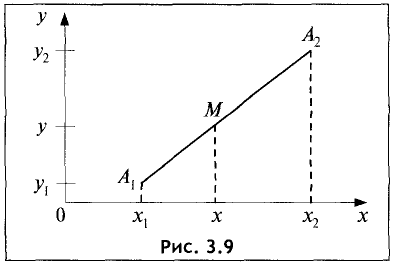
Прямые, проведенные из точек  перпендикулярно оси
перпендикулярно оси
Ох, делят прямые Ох и 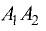 на пропорциональные отрезки, т.е.
на пропорциональные отрезки, т.е.
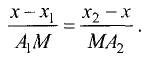
Преобразуем это выражение к виду
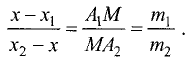
Отсюда находим
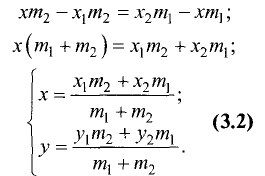
Точка M может быть расположена и вне отрезка 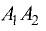 (рис. 3.10).
(рис. 3.10).
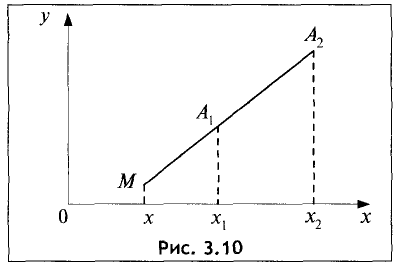
В этом случае отношение 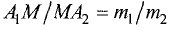 является отрицательной
является отрицательной
величиной, так как отрезки 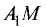 и
и 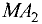 имеют противоположное направление.
имеют противоположное направление.
Пример:
Даны точки А(4; 2), В(10; 5). Найти точки 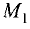 и
и 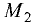 ,
,
делящие отрезок в отношении 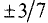 внутренним и внешним образом.
внутренним и внешним образом.
Решение:
Геометрия задачи представлена на рис. 3.11.
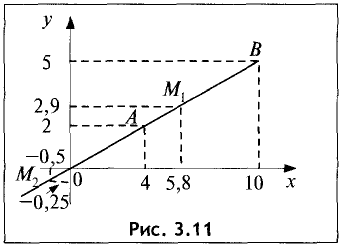
При делении отрезка внутренним образом координаты точки 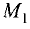 находятся по формулам (3.1) и (3.2):
находятся по формулам (3.1) и (3.2):
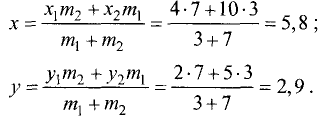
При делении отрезка внешним образом координаты точки 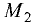 также находятся по формулам (3.1) и (3.2), но
также находятся по формулам (3.1) и (3.2), но 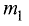 или
или 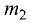 принимается отрицательным.
принимается отрицательным.
Угол наклона отрезка к оси абсцисс
Проведем через точки 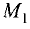 и
и  две прямые, параллельные оси
две прямые, параллельные оси
Оу, и две прямые, параллельные оси Ох (рис. 3.12).
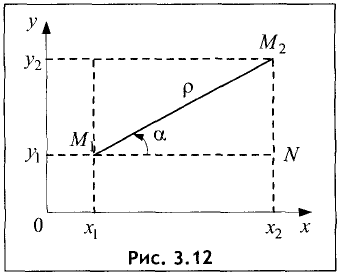
Отрезок 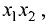 лежащий на оси Ох, называется проекцией отрезка
лежащий на оси Ох, называется проекцией отрезка 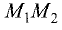 на ось Ох. Его длина равна
на ось Ох. Его длина равна 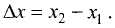 Аналогично
Аналогично 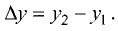
Из прямоугольного треугольника 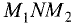 следует:
следует:
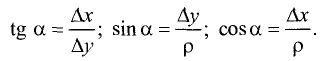
Уравнение прямой
В общем случае уравнение прямой записывают в виде
Ах + Ву + С = 0. (3.3)
Преобразуем это уравнение относительно у:
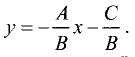
Введем обозначения:
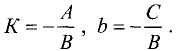
Тогда
у = Кх + b. (3.4)
Это наиболее часто встречаемый вид уравнения прямой. Графически прямая представлена на рис. 3.13.
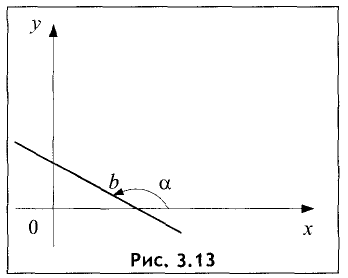
Коэффициент К, входящий в уравнение прямой, называется угловым коэффициентом и равен тангенсу угла между осью Ох и прямой K=tg a (рис. 3.13).
Коэффициент b — это координата точки пересечения прямой с осью Оу. В этом легко убедиться, положив х = 0, т.е.
y(0) = 0*x + b = b .
Уравнение прямой, параллельной оси Ох, следует из уравнения (3.4) при К = tg а = tg 0 = 0 и имеет вид
y = b. (3.5)
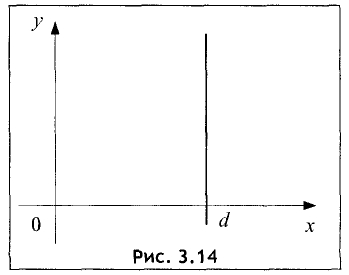
Уравнение прямой, параллельной оси Оу, следует из общего уравнения прямой (3.3) при b = 0. Тогда Ах + С = 0 . Решив это уравнение относительно х, получим
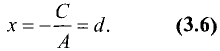
График этой прямой представлен на рис. 3.14
Пример:
Написать уравнение прямой, образующей с осью абсцисс угол  и отсекающей начальную ординату b = 4. Начертить график.
и отсекающей начальную ординату b = 4. Начертить график.
Решение:
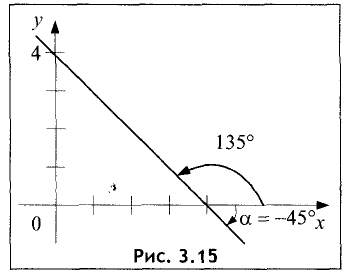
Положительное направление угла отсчитывается от оси Ох против часовой стрелки, а отрицательное — по часовой стрелке (рис. 3.15).
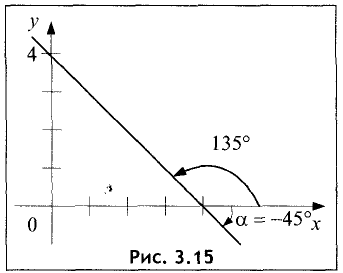
Угловой коэффициент К=tg(-45)°=tgl35° = -1. Уравнение прямой имеет вид у=-х+4.
Точка пересечения прямой с осью ОХ находится из условия у=0. Ее координата равна х=4. График прямой предоставлен на рис. 3.15. ►
Пример:
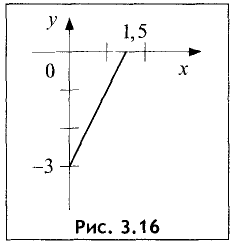
Начертить график прямой у=2х-3.
Решение:
Ось Оу прямая пересекает в точке у=-3, а ось Ох — в точке х=3\2=1,5. Отметив на осях оказанные координаты, проводим прямую через две точки (рис. 3.16) ►
Пример:
Найти точку пересечения двух прямых:

Решение:
Точкой пересечения является решение системы из двух линейных уравнений (3.7). Вычитая из второго уравнения первое, получим 2х— 3+х — 4 = 0. Решив это уравнение, получим абсциссу точки пересечения прямых: х = 7/3.
Подставив значение абсциссы точки пересечения прямых в первое уравнение (3.7), получим значение ординаты точки пересечения, т.е.
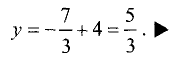
Условие перпендикулярности прямых
Даны две прямые
Если эти прямые перпендикулярны, то угол наклона одной из них должен отличаться от угла наклона другой на 90°, т.е.  Тогда
Тогда 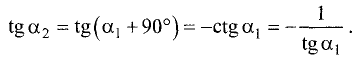 Умножив правую и левую части этого уравнения на
Умножив правую и левую части этого уравнения на 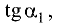 получим условие перпендикулярности двух прямых:
получим условие перпендикулярности двух прямых:

Пример:
Найти угол наклона прямой, перпендикулярной к прямой у = х +1.
Решение:
Так как 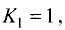 то в соответствии с (3.8)
то в соответствии с (3.8) 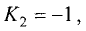 т.е.
т.е. 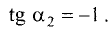 Отсюда находим
Отсюда находим 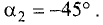 ►
►
Угол между прямыми
Пусть две прямые заданы уравнениями:
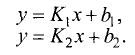
Если угол между прямыми равен 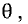 то справедливо соотношение (рис. 3.17)
то справедливо соотношение (рис. 3.17)
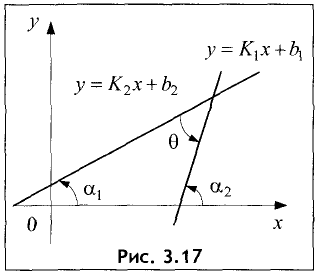
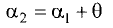 или
или 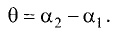 Взяв тангенс от левой и правой частей последнего соотношения, получим
Взяв тангенс от левой и правой частей последнего соотношения, получим
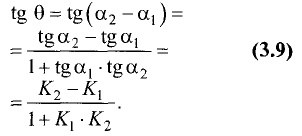
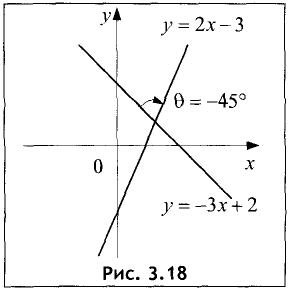
Пример:
Найти угол, образованный прямой у = -3х + 2 с прямой у = 2х~3 .
Решение:
Так как 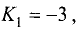 а
а 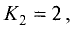 то
то
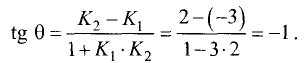
Отсюда находим 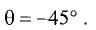 Графически решение представлено на рис. 3.18. ►
Графически решение представлено на рис. 3.18. ►
Пучок прямых
Совокупность всех прямых, проходящих через данную точку  , называется центральным пучком прямых или просто пучком. Точка
, называется центральным пучком прямых или просто пучком. Точка  называется центром пучка.
называется центром пучка.
Уравнение

в котором угловой коэффициент К рассматривается как величина, способная принимать любые числовые значения, называется уравнением пучка с центром  Этим уравнением нельзя представить только прямую, параллельную оси Оу.
Этим уравнением нельзя представить только прямую, параллельную оси Оу.
Пример:
Указать точку, через которую проходят все прямые, представленные уравнением y + 3 = K(x + 1).
Решение:
Сопоставив уравнение примера с (3.10), определим координаты центра, равные (-1; -3). ►
В общем виде уравнение пучка прямых можно записать в виде
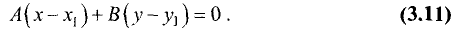
Найдем уравнение прямой, перпендикулярной прямой
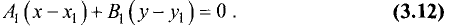
Пусть уравнение искомой прямой имеет вид
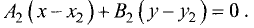
Если 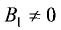 и
и 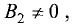 то данные уравнения можно представить в стандартной форме
то данные уравнения можно представить в стандартной форме
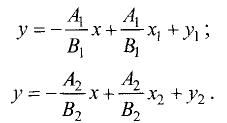
Используя (3.8), условие перпендикулярности двух рассматриваемых прямых можно представить в виде
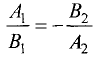 или
или 
Условие (3.13) будет выполняться, если положить 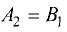 и
и  Тогда уравнение прямой, перпендикулярной прямой (3.13), можно представить как
Тогда уравнение прямой, перпендикулярной прямой (3.13), можно представить как
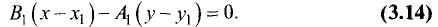
Уравнение прямой, проходящей через две данные точки
Пусть имеются две точки 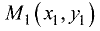 и
и 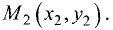 Определить уравнение прямой, проходящей через эти точки.
Определить уравнение прямой, проходящей через эти точки.
Уравнение пучка прямых, проходящих через точку 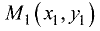 , имеет вид
, имеет вид
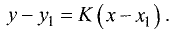
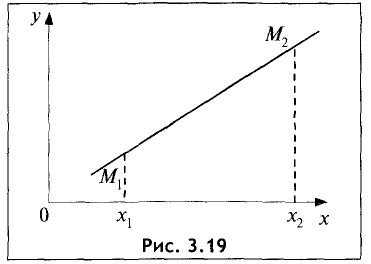
Одна из этих прямых проходит также через точку 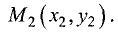 В этом случае можно записать:
В этом случае можно записать:
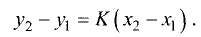
Из полученного уравнения определяем угловой коэффициент искомой прямой.
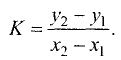
Подставив полученную формулу для углового коэффициента в уравнение пучка прямых, найдем
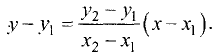
Окончательно уравнение прямой, проходящей через две заданные точки, записывают в виде

Пример:
Составить уравнение прямой, проходящей через
точки: а) 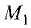 (4; — 2) и
(4; — 2) и 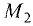 (-1; 7), б)
(-1; 7), б) 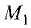 (-4; — 5) и
(-4; — 5) и 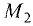 (-4; -1).
(-4; -1).
Решение:
а) Подставив данные примера в (3.15), найдем 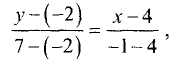 или
или 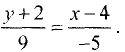 Решив последнее уравнение относительно у, получим
Решив последнее уравнение относительно у, получим
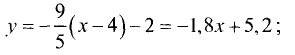
б) подставив данные в (3.15), получим 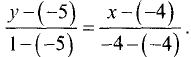 Так как
Так как
знаменатель в правой части равен нулю, а на ноль делить нельзя, то эта прямая параллельна оси Оу, что и следует из рис. 3.20.
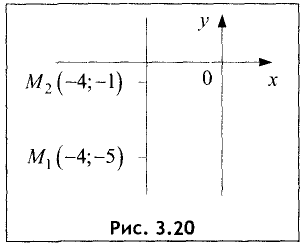
Уравнение искомой прямой имеет вид х = -4 . ►
Пример:
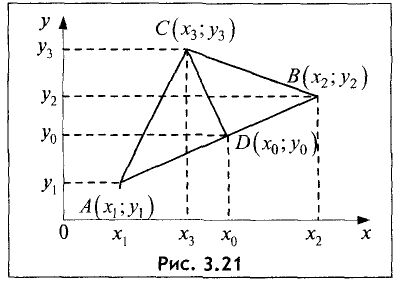
Определить площадь S треугольника АВС с вершинами 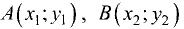 и
и 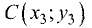 при
при 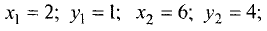
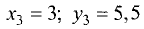 (рис. 3.21).
(рис. 3.21).
Решение:
Площадь треугольника определяем по формуле
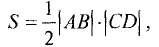
где 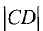 — высота треугольника. Неизвестными здесь являются координаты
— высота треугольника. Неизвестными здесь являются координаты 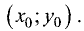 Их можно найти как точку пересечения прямой, проходящей через точки А и В, и перпендикулярной к ней прямой, проходящей через точку С. Уравнение прямой, проходящей
Их можно найти как точку пересечения прямой, проходящей через точки А и В, и перпендикулярной к ней прямой, проходящей через точку С. Уравнение прямой, проходящей
через точки А и В, имеет вид
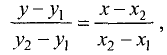
а ее угловой коэффициент определяется формулой
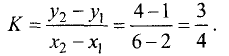
Таким образом, уравнение прямой, проходящей через точки А и В,
можно представить в виде 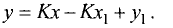
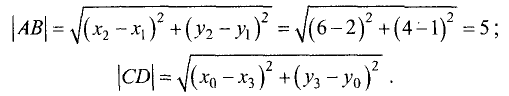
Угловой коэффициент прямой, перпендикулярной к рассматриваемой, определяем по формуле
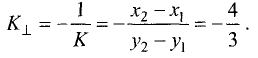
Уравнение данной прямой имеет вид
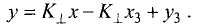
Координаты точки D находим из системы двух линейных уравнений:
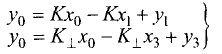
Вычитая из второго уравнения первое, получим
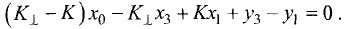
Отсюда находим
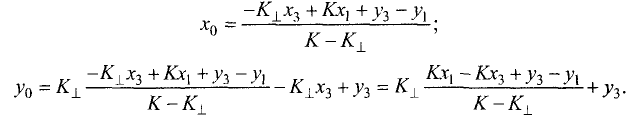
Для условий примера имеем 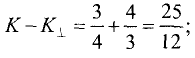
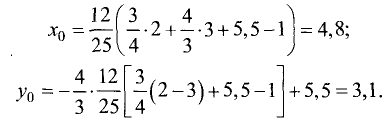
Определим высоту треугольника
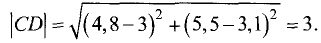
Площадь треугольника равна
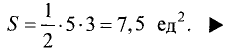
Расстояние от точки до прямой
Найти расстояние d от данной точки 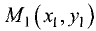 до данной прямой
до данной прямой
Ах + Ву + С = 0. (3.16)
Расстояние d находим по формуле (рис. 3.22):
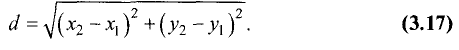
Точка 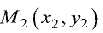 — основание перпендикуляра,
— основание перпендикуляра,
опущенного из точки 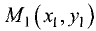 на прямую (3.16).
на прямую (3.16).
В соответствии с (3.14) уравнение прямой, перпендикулярной (3.16), имеет вид
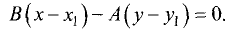
Координаты точки 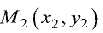 находим из решения системы уравнений
находим из решения системы уравнений
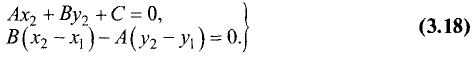
Введем замену: 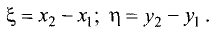 Тогда (3.17) и (3.18)
Тогда (3.17) и (3.18)
можно записать в виде
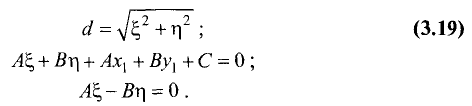
Решая систему из двух последних уравнений, находим
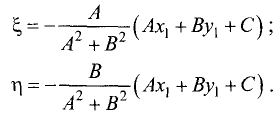
Подставив эти значения в (3.19), получим
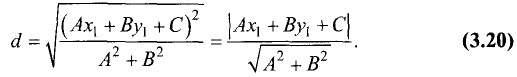
Пример:
Найти расстояние от точки М (—1; 1) до прямой
4х-3у+6 = 0.
Решение:
Искомое расстояние находится по формуле (3.20):
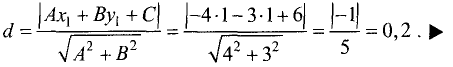
Уравнение окружности
Пусть дана окружность радиуса R с координатами центра C(a,b) (рис.
3.23).
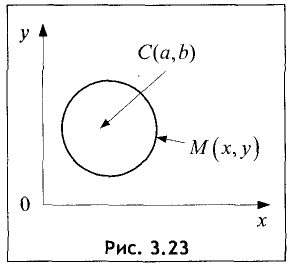
Найдем ее уравнение. По определению окружности для С(а,b) любой ее точки М(а,b) расстояние от центра до этой точки постоянно и
равно радиусу окружности R. Как следует из формулы (3.1), это
расстояние равно
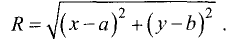
Возводя в квадрат правую и левую части этого равенства,
получим уравнение окружности
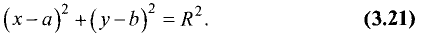
Если центр окружности лежит в начале координат, то а = b = 0 ,
а уравнение окружности приобретает вид
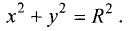
Уравнение вида
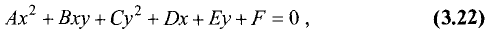
если хотя бы одна из трех величин А, В или С не равна нулю,
называется уравнением второго порядка, а линия, представляемая таким уравнением, — линией второго порядка. Выясним, при каких
условиях это уравнение является уравнением окружности. Для этих целей уравнение (3.21) представим в виде
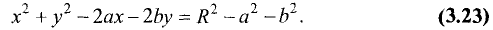
В уравнении (3.22) положим 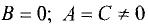 и разделим правую
и разделим правую
и левую части на А. В результате получим
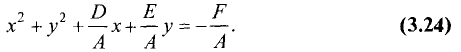
Уравнение (3.24) имеет тот же вид, что и уравнение (3.23), т.е.
является уравнением окружности. Сопоставив (3.23) с (3.24), найдем
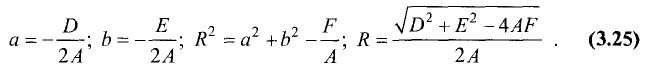
Пример:
Является ли уравнение 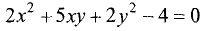
окружностью?
Решение:
Не является, так как в нем содержится слагаемое,
содержащее ху. ►
Пример:
Является ли уравнение 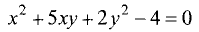
окружностью?
Решение:
Не является, так как коэффициенты при 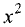 и
и 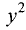 не
не
равны. ►
Пример:
Найти координаты центра и радиус окружности
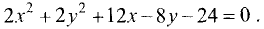
Решение:
Преобразуем исходное уравнение следующим образом:
1. Делим правую и левую части на 2:
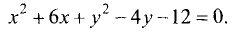
2.Дополняем выражения 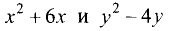 до квадратов:
до квадратов:
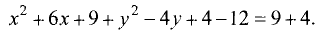
3.Приводим уравнение к виду (3.21):
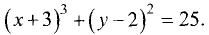
Отсюда следует, что исходное уравнение является окружностью
радиуса 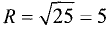 с центром в точке (—3; 2). ►
с центром в точке (—3; 2). ►
Уравнение эллипса
Эллипсом называется геометрическое место точек, для которых сумма расстояний для двух точек F и F’ равна постоянной величине 2а.
Пусть две точки F и F’ отстоят на расстояние 2с друг от друга
(рис. 3.24).
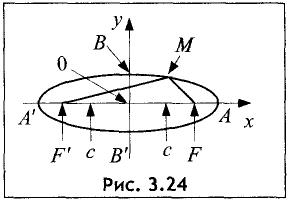
Сумма расстояний 2а от этих точек до любой точки эллипса
всегда больше 2с. В противном случае искомого геометрического места точек не существует. Найти уравнение эллипса.
Принимаем прямую FF’ за ось абсцисс, середину отрезка FF’ —
за начало координат. Тогда координаты точек F и F’ примут
значения
F'(-c, 0); F(c; 0).
По определению эллипса сумма расстояний для двух точек
F и F’ равна постоянной величине 2а, т.е.
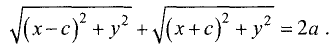
Перепишем его в виде
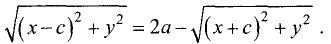
Возведем в квадрат левую и правую части последнего равенства
и сгруппируем члены:
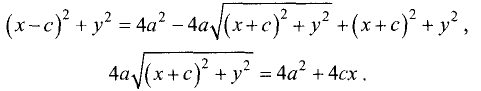
Сократим на 4, возведем в квадрат и приведем подобные члены
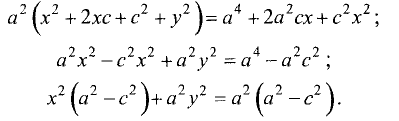
Разделив правую и левую части на 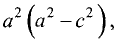 получим
получим
уравнение эллипса:
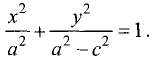
Из определения эллипса и геометрии рис. 3.24 следует, что при
совмещении точки М с точкой А большая ось эллипса А’А = 2а , т.е.
большая полуось равна а. Введем обозначение

Тогда уравнение эллипса принимает вид

Как следует из треугольника OBF и соотношения (3.26), малая
полуось эллипса ОВ равна b.
Точки F и F’ называются фокусами эллипса, а расстояние FF’ = 2с — фокусным расстоянием. Отношение фокусного расстояния к большой оси называется эксцентриситетом эллипса и обозначается буквой 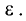 Таким образом, можно записать
Таким образом, можно записать
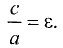
Пример:
Определить эксцентриситет окружности.
Решение:
Так как в окружности а = b, то, как следует из соотношения (3.21), с = 0, т.е. 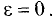 ►
►
Пример:
Фокусное расстояние эллипса равно 8 см, малая ось
равна 6 см. Найти большую ось и эксцентриситет.
Решение:
Так как фокусное расстояние FF’ = 2с = 8 , то с = 4, а
малая полуось b=3. Из соотношения (3.26) находим длину большой
полуоси:
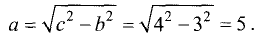
Большая ось равна 2а = 10 см.
Эксцентриситет находим по формуле
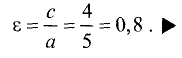
Уравнение гиперболы
Гиперболой называется геометрическое место точек М, для которых
разность расстояний до двух точек F и F’, называемых фокусами, имеет одну и ту же абсолютную величину 2а.
Пусть две точки F и F’ отстоят на расстояние 2с друг от друга (рис. 3.25).
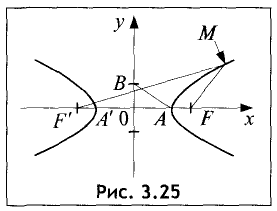
Разность расстояний 2а от этих точек до любой точки гиперболы
всегда меньше 2с. В противном случае искомого геометрического места точек не существует. Найти уравнение гиперболы.
Принимаем прямую FF’ за ось абсцисс, середину отрезка FF’ —
за начало координат. Тогда координаты точек F и F’ примут значения
F'(-c;0);F(c;0).
По определению гиперболы разность расстояний для двух точек
F и F’ равна постоянной величине 2а, т.е. для правой ветви
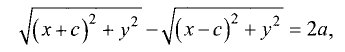
для левой ветви
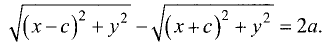
Проведя те же преобразования, что и в предыдущем параграфе,
получим
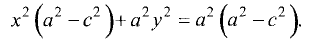
В отличие от эллипса здесь разность 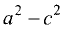 отрицательна, так
отрицательна, так
как а < с .
Разделив правую и левую части на 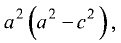 получим уравнение гиперболы:
получим уравнение гиперболы:
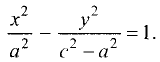
Отрезок А’А называется действительной осью гиперболы. Из определения гиперболы и геометрии рис. 3.25 следует, что при совмещении точки М с точкой А действительная ось гиперболы А’А = 2а , т.е. действительная полуось равна а. Введем обозначение:

Тогда уравнение гиперболы принимает вид

Отрезок В’В = 2b называют мнимой осью гиперболы.
В силу (3.29) отрезок АВ = с (рис. 3.25).
Отношение фокусного расстояния FF’ к действительной оси
называется эксцентриситетом гиперболы и обозначается буквой 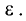
Таким образом, можно записать
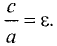
В отличие от эллипса эксцентриситет гиперболы больше единицы.
Пример:
Определить эксцентриситет равносторонней
гиперболы, у которой а = b.
Решение:
Эксцентриситет равносторонней гиперболы
определяется соотношением
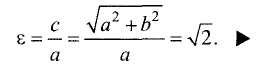
Асимптотой гиперболы называется прямая, проходящая через начало координат и неограниченно сближающаяся с ветвями гиперболы при  (рис. 3.26).
(рис. 3.26).
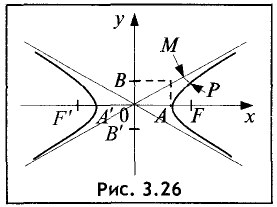
Прямые, проходящие через центр гиперболы и точки с координатами (а, b), (-а, b), (-а, -b), (а, -b) являются асимптотами.
Доказательство:
Уравнение данной прямой 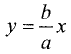 и уравнение гиперболы (3.30) запишем в виде
и уравнение гиперболы (3.30) запишем в виде
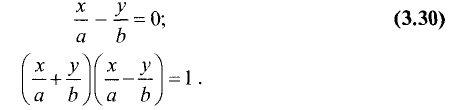
Откуда

Так как сумма  при
при 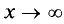 и
и 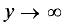 остается положительной величиной, то разность в (3.31) стремится к нулю и так же остается положительной. Но расстояние MP = d от точки М до прямой (3.30) пропорционально этой разности. Действительно, в
остается положительной величиной, то разность в (3.31) стремится к нулю и так же остается положительной. Но расстояние MP = d от точки М до прямой (3.30) пропорционально этой разности. Действительно, в
соответствии с (3.20) это расстояние равно
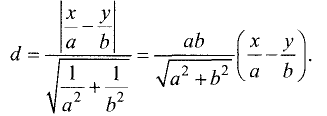
Отсюда видно, что расстояние MP = d стремится к нулю, когда
точка М удаляется в бесконечность, т.е. прямая (3.30) является
асимптотой. Аналогично доказываются и другие случаи.
Пример:
Фокусное расстояние гиперболы равно 10 см, мнимая
ось — 6 см. Найти действительную ось, эксцентриситет и асимптоты.
Решение:
Так как фокусное расстояние FF’ = 2с = 10 , то с = 5,
а мнимая полуось b = 3. Из соотношения (3.28) находим длину
действительной полуоси:
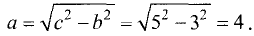
Большая ось равна 2а = 8 см.
Эксцентриситет находим по формуле
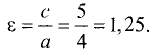
Асимптоты определяются по формуле
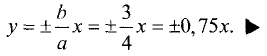
Уравнение параболы
Параболой называется геометрическое место точек М, равноудаленных от данной точки F, называемой фокусом, и прямой PQ, называемой директрисой параболы. Расстояние FC = р от фокуса до директрисы называется параметром параболы.
Пусть прямая PQ и точка F отстоят на расстоянии р от искомого геометрического места точек (рис. 3.27).
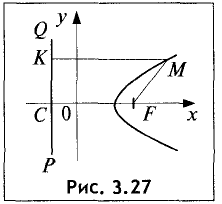
Найти уравнение параболы.
Примем за начало координат середину отрезка CF. 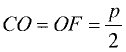 фокусное расстояние. Ось абсцисс направим по лучу OF.
фокусное расстояние. Ось абсцисс направим по лучу OF.
Тогда фокус F будет иметь следующие координаты: 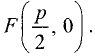 Расстояние FM определяется выражением
Расстояние FM определяется выражением 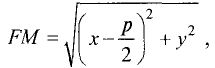
расстояние КМ — выражением 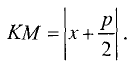 По определению
По определению
параболы эти два расстояния равны друг другу, т.е. 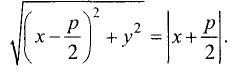
Данное выражение является уравнением параболы. Возведя
левую и правую части в квадрат и приведя подобные члены, получим каноническое уравнение параболы:

Пучок лучей с источником, расположенном в фокусе, после
отражения от параболы обратится в параллельный пучок лучей. На
этом принципе построены параболические зеркальные антенны.
Пример:
Написать каноническое уравнение параболы с
фокусным расстоянием, равным 3.
Решение:
Так как фокусное расстояние равно 3, то параметр
параболы р = 2 • 3 = 6. Используя уравнение (3.32), получим
каноническое уравнение параболы
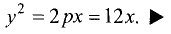
Уравнение плоскости в трехмерной системе координат
Положение точки в пространстве определяется тремя координатами.
Прямоугольная система координат в пространстве представляет
из себя три перпендикулярные прямые, снабженные масштабами и
направлениями. Такие прямые называются координатными осями.
Координатами точки называются координаты оснований
перпендикуляров, опущенных из этой точки на координатные оси.
Всякое уравнение, линейное относительно координат, определяет плоскость, и, наоборот, уравнение любой плоскости есть уравнение первой степени.
Общее уравнение плоскости имеет вид (рис. 3.28)
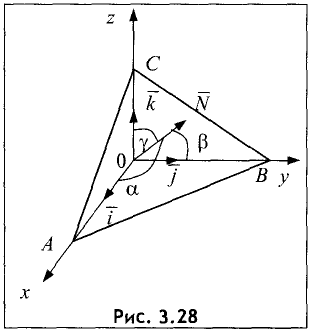
Ax + By + Cz + D = 0. (3.33)
Уравнение плоскости может быть представлено в векторной
форме
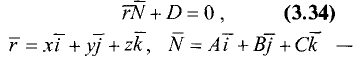
вектор, перпендикулярный плоскости.
Если D = 0, то плоскость проходит через начало координат.
Если A = 0 (В = 0,С = 0), то плоскость параллельна относительно оси Ox (Оу, Oz).
Пример:
Составить уравнение плоскости, проходящей через
начало координат и перпендикулярной вектору 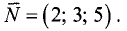
Решение:
Из (3.34) следует, что уравнение плоскости, проходящей через начало координат, определяется соотношением 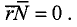
Поэтому искомое уравнение имеет вид
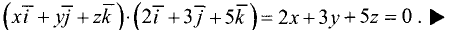
Нормальное уравнение плоскости имеет вид
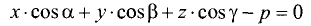 или
или 
где 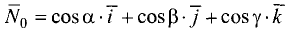 — единичный вектор, перпендикулярный плоскости; р — расстояние плоскости от начала координат.
— единичный вектор, перпендикулярный плоскости; р — расстояние плоскости от начала координат.
Уравнение плоскости в отрезках:

где а, b и с — отрезки, отсекаемые плоскостью на осях координат с
учетом знака.
Пример:
Составить уравнение плоскости, отсекающей от
каждой оси одинаковое число линейных единиц.
Решение:
Так как а = b = с , то уравнение плоскости имеет вид
x+y+z=а.►
Две плоскости, представляемые уравнениями
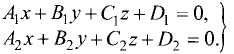
образуют четыре двугранных угла, равных попарно. Когда говорят
об угле между двумя плоскостями, то имеют в виду любой из этих
углов и приписывают ему значение 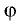 , заключенное между 0 и 180°.
, заключенное между 0 и 180°.
Одно из значений 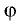 равно углу между нормальными векторами
равно углу между нормальными векторами
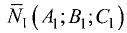 и
и 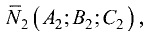 другое значение
другое значение  дополняет первое до 180°. Данный угол определяют по формуле
дополняет первое до 180°. Данный угол определяют по формуле
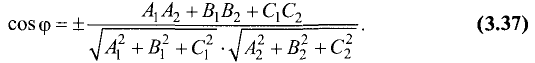
Пример:
Найти угол между плоскостями, заданными
уравнениями
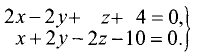
Решение:
Подставив в (3.38) соответствующие коэффициенты,
получим
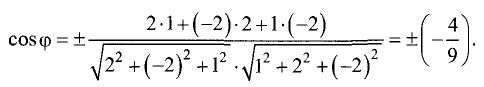
Таким образом, 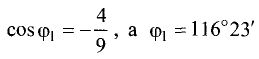 (это угол между нормальными векторами
(это угол между нормальными векторами 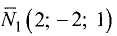 и
и 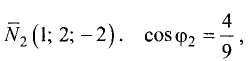 a
a 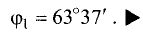
Расстояние от точки 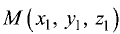 до плоскости
до плоскости
Ax + By + Cz + D = 0
определяется по формуле
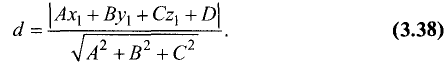
Пример:
Найти расстояние от точки М (2,1,1) до плоскости
2х + 2у- z-2 = 0.
Решение:
Подставив исходные данные в формулу (3.38), получим
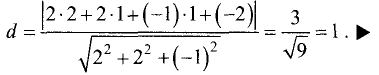
Уравнение прямой в пространстве
Всякая прямая линия представляется системой двух уравнений
первой степени
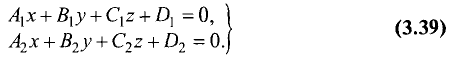
которые, взятые по отдельности, представляют какие-либо две
плоскости, проходящие через эту прямую.
Если коэффициенты 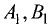 и
и 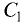 пропорциональны коэффициентам
пропорциональны коэффициентам 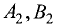 и
и 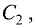 а свободные члены не подчиняются той же пропорции
а свободные члены не подчиняются той же пропорции
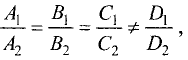
то плоскости параллельны и никогда не пересекутся, т.е. такая
система не представляет прямой линии.
Направляющим вектором прямой называется всякий ненулевой вектор 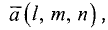 лежащий на этой прямой или параллельный ей. Координаты l, m, n направляющего вектора называются направляющими коэффициентами прямой.
лежащий на этой прямой или параллельный ей. Координаты l, m, n направляющего вектора называются направляющими коэффициентами прямой.
За направляющий вектор прямой (3.39) можно принять векторное
произведение нормальных векторов 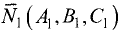 и
и 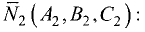
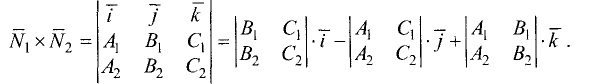
Отсюда находим
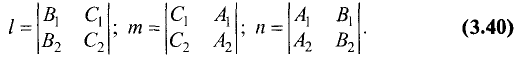
Пример:
Найти направляющие коэффициенты прямой
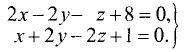
Решение:
По формулам (3.40) находим
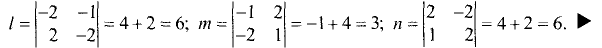
Под углами 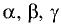 между прямой и осями координат понимают
между прямой и осями координат понимают
углы между направляющим вектором 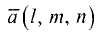 и ортами
и ортами 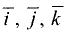
соответственно. Косинусы этих углов вычисляются по формулам
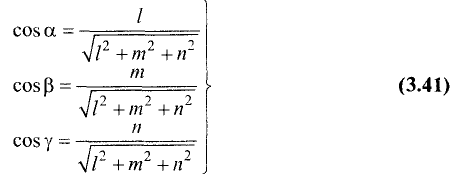
Пример:
Для условий примера 3.27 найти направляющие
косинусы и углы, образуемые прямой с осями координат.
Решение:
По формулам (3.41) находим
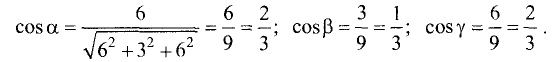
Находя арккосинусы, получим
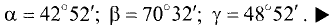
Под углом между двумя прямыми понимается угол между их
направляющими векторами  и
и  В
В
зависимости от выбора направления векторов (каждый из них может иметь два взаимно противоположных направления) этот угол может иметь два значения, дополняющих друг друга до 180°. Косинус угла между прямыми вычисляется по формуле
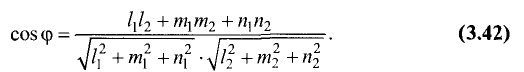
Пример:
Даны две прямые с направляющими векторами
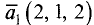 и
и 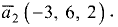 Определить угол между ними.
Определить угол между ними.
Решение:
Подставим данные примера в формулу (3.42):
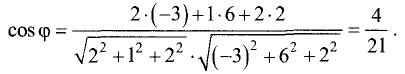
Отсюда находим 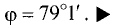
Углом между прямой L и плоскостью Р называют острый угол 
между прямой L и ее проекцией L’
на плоскость Р (рис. 3.29).
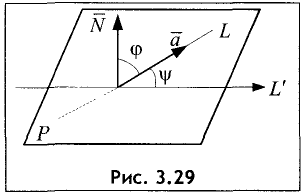
Пусть даны направляющий вектор 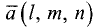 прямой L и
прямой L и
нормальный вектор 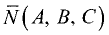 плоскости Р. Косинус угла
плоскости Р. Косинус угла 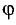 между этими векторами равен
между этими векторами равен
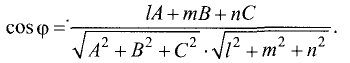
Как следует из рис. 3.29, 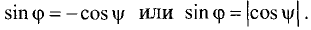 Тогда
Тогда
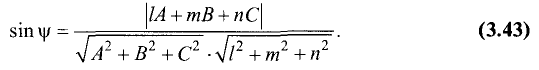
Пример:
Найти угол между прямой
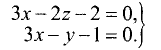
и плоскостью 2x + y + z + 5—0.
Решение:
Направляющими коэффициентами прямой являются числа
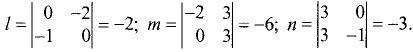
Координаты нормального вектора плоскости:
А = 2, 5 = 1, С = 1 .
Подставив полученные цифры в (3.43), найдем

Отсюда следует 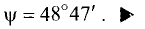
Проекция прямой
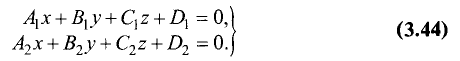
(коэффициенты 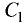 и
и 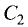 не равны нулю одновременно) на
не равны нулю одновременно) на
координатную плоскость хОу находится по следующему правилу: чтобы найти проекцию прямой (3.44) на координатную плоскость хОу
достаточно исключить z из уравнений (3.44); полученное
уравнение совместно с уравнением z = 0 представляет искомую
проекцию.
Аналогично находятся проекции прямой на координатные
плоскости yOz и zOx.
Пример:
Найти проекции прямой
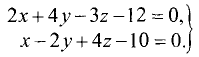
на координатные плоскости.
Решение:
Исключив z из системы уравнений, получим уравнение проекции данной прямой на плоскость хОу :
11х + 10у-78 = 0.
Исключив у из системы уравнений, получим уравнение проекции
данной прямой на плоскость zOx :
4x + 5z-32 = 0.
Исключив х из системы уравнений, получим уравнение проекции
данной прямой на плоскость yOz :
8y-11z + 8 = 0. ►
Пусть задан направляющий вектор 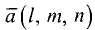 прямой,
прямой,
проходящий через точку 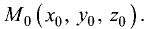 Такая прямая описывается симметричными (каноническими) уравнениями вида
Такая прямая описывается симметричными (каноническими) уравнениями вида
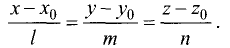
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

