Оглавление:
Неравенство в математике — это отношение, связывающее два числа или иных математических объекта с помощью одного из перечисленных ниже знаков.
Неравенства первой степени
Мы уже говорили, в каком смысле надо понимать выражение „больше“ и „меньше“ применительно к относительным числам, а именно: выражение „а больше b“ (а>b) означает, что разность а — b есть число положительное, а выражение „а меньше b“ (α<b) означает, что эта разность-число отрицательное.
Основные свойства неравенств. Два числа или два алгебраических выражения, связанные между собой знаком > или <, образуют неравенство. Неравенство состоит из двух частей: левой части и правой части.
Обозначим левую часть неравенства буквой а и правую часть буквой b. Тогда основные свойства неравенств мы можем выразить так:
1) Если а > b, то b < а; например: —2 > —3; — 3 <—2.
2) Если a > b и b > с, то а > с; например: — 2 > —Зи—3 > —4; тогда—2 > —4.
3) Если α > b и c=d, то α + с > b+d и а — с > b — d, т. е. если к неравным числам прибавим или вычтем из них равные числа, то знак неравенства не изменится (большее число останется большим). Например: 2>—3; прибавим или вычтем по —10:
2+(-10) >-3+(-10), т. е. -8>-13;
2—( — 10) >-3 -(-10), т. е. 12 > 7.
4) Если a > b и с > d, то a + c > b + d; равным образом, если a < b и с < d, то a + c < b + d.
Например, если части двух неравенств: —7 > — 10 и —3 > —4 почленно сложим, то получим: —10 > —14.
Равным образом, если сложим почленно части двух неравенств 2<8 и —4 < —2, то будем иметь: —2 <6.
5) Если а > b, а с < d, то а—с > b—d; или если a < b, а с > d, то а—c<b—d.
Например: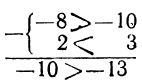 или
или 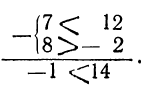
Условимся о двух неравенствах говорить, что они одинакового смысла, если в каждом из них имеется один и тот же знак > или <, и что они противоположного смысла, если в одном из неравенств стоит знак > в другом знак < . Тогда свойства четвёртое и пятое можно высказать так:
Два неравенства одинакового смысла можно почленно складывать; два неравенства противоположного смысла можно почленно вычитать, оставляя знак того неравенства, из которого вычиталось другое неравенство.
6) Если α > b и m — положительное число, то am> bm и a : m > b : m .
Если обе части неравенства умножим или разделим на одно и то же положительное число, то знак неравенства не изменится.
Например, умножив на +4 части неравенства —5 > —7, получим: —20 >—28.
7) Если a > b и m — отрицательное число, то am < bm и a : m < b : m .
Если обе части неравенства умножим или разделим на одно и то же отрицательное число, то знак неравенства переменится на противоположный.
Например, умножив на —1 обе части неравенства —5 >—7, получим: 5 < 7.
Относительно неравенств (как и равенств), содержащих буквы, возможны вопросы двух родов:
1) решить неравенство, содержащее неизвестное, т. е. определить, при каких значениях неизвестных данное неравенство справедливо;
2) доказать тождественное неравенство, т. е. обнаружить верность его при всевозможных значениях букв или по крайней мере при значениях, ограниченных заданными наперёд условиями.
Решение обоих вопросов основывается на некоторых свойствах неравенств, подобных тем, которые служат основанием для решения уравнений.
Равносильные неравенства
Неравенства, содержащие одни и те же неизвестные, называются равносильными, если они удовлетворяются одними и теми же значениями этих неизвестных; так, два неравенства 3x+3<x+10 и 3x < x+8 равносильны, так как оба они удовлетворяются значениями х, меньшими 4, и только этими значениями.
Относительно равносильности неравенства докажем теоремы, весьма сходные с подобными же теоремами относительно равносильности уравнений.
Теорема:
Если к обеим частям неравенства (содержащего неизвестные) прибавим (или отнимем) одно и тоже число, то получим новое неравенство, равносильное первому.
Обозначим левую часть неравенства, содержащего неизвестные, одной буквой А и правую часть—другой буквой В, и пусть m есть какое угодно число; докажем, что два неравенства:
A>B (1)
и
А+m > B + m (2)
равносильны. Положим, что первое неравенство удовлетворяется при некоторых значениях букв. Это значит, что при этих значениях численная величина А больше численной величины В; но тогда, на основании свойства 3, при тех же значениях букв и численная величина суммы A+m больше численной величины суммы B+m, так как если к обеим частям неравенства прибавим поровну, то знак неравенства не изменится. Значит, всякое решение неравенства (1) удовлетворяет и неравенству (2).
Обратно, если при некоторых значениях букв численная величина суммы A+m больше численной величины суммы B+m, то для тех же значений букв и численная величина А больше численной величины В (неравенство не нарушится, если к обеим частям неравенства прибавим— m следовательно, все решения неравенства (2) удовлетворяют и неравенству (1); значит, эти неравенства равносильны.
Так как вычитание равносильно сложению с противоположным числом, то, следовательно, от обеих частей неравенства можно отнять одно и то же число.
Следствие. Любой член неравенства можно перенести из одной части в другую с противоположным знаком.
Если, например, имеем неравенство A > B + C, то, прибавив к обеим частям по—С, получим: А—С > В.
Теорема:
Если обе части неравенства (содержащего неизвестные) умножим (или разделим) на одно и то же положительное число, то получим новое неравенство, равносильное первому.
Докажем, что два неравенства:
A>B (1)
и
Аm > Bm (2)
равносильны, если только m—положительное число.
Пусть при некоторых значениях неизвестных численная величина А больше численной величины В; тогда при тех же значениях неизвестных и численная величина произведения Am больше численной величины произведения Вm , так как от умножения обеих частей неравенства на положительное число знак неравенства не изменяется. Значит, все решения неравенства (1) удовлетворяют и неравенству (2).
Обратно, если при некоторых значениях букв численная величина Am больше численной величины Вm, то при тех же значениях букв и численная величина А больше численной величины В, так как от деления обеих частей неравенства на положительное число знак неравенства не изменяется.
Замечание:
Положительное число, на которое, по доказанному, мы имеем право умножить или разделить обе части неравенства (не изменяя его знака), может быть дано в виде буквенного выражения, причём это выражение может содержать в себе и неизвестные, входящие в неравенство. Но при этом надо особо рассмотреть, при всех ли значениях . букв, входящих в выражение, на которое мы умножаем или делим обе части неравенства, это выражение имеет положительные значения.
Например, умножим обе части неравенства A>B на выражение (х-5):
A>B (1)
A(x-5)² > B(x-5)² ,∙ (2)
Множитель, (х—5)² остаётся положительным числом при всех значениях х, кроме одного: х=5. Значит, неравенства (1) и (2) равносильны в том случае, если первое из них не удовлетворяется значением х=5; в противном же случае неравенство (1), удовлетворяясь всеми решениями неравенства (2), имеет ещё решение: х = 5 (это решение неравенству (2) не удовлетворяет, ибо при х = 5 неравенство (2) обращается в равенство).
Следствие. Если обе части неравенства содержат положительный общий множитель, то на него можно разделить обе части неравенства.
Например, в обеих частях неравенства: (х—5)² (х—1)>(x-5)² (3-х) есть общий множитель (х—5)² . Этот множитесь при х=5 обращается в 0, а при всех остальных значениях х он — число положительное. Решение х=5 не удовлетворяет данному неравенству. Желая решить, удовлетворяется ли неравенство при других значениях х, мы можем разделить обе его части на (х—5)² , как на число положительное; после деления получим: х—1>3—х. -Все значения х, удовлетворяющие этому неравенству, за исключением x=5, удовлетворяют и данному неравенству.
Теорема:
Если обе части неравенства (содержащего неизвестные) умножим (или разделим) на одно и то же отрицательное число и при этом переменим знак неравенства на противоположный, то получим новее неравенство, равносильное первому.
Эта теорема доказывается совершенно так же, как и теорема 2; надо только принять во внимание, что от умножения или деления обеих частей неравенства на отрицательное число знак неравенства изменяется на противоположный.
По поводу этой теоремы можно высказать такое же замечание, какое было сделано по отношению к теореме 2.
Следствия. а) Переменив у всех членов неравенства знаки на противоположные (т. е. умножив обе его части на —1), мы должны изменить знак неравенства на противоположный.
б) Нельзя умножить обе части неравенства на буквенный множитель, знак которого неизвестен.
в) Неравенство с дробными членами можно привести к целому виду. Возьмём, например, такое неравенство: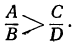 (1)
(1)
Перенесём все члены в левую часть и приведём их к общему знаменателю: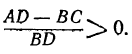 (2)
(2)
Если BD — положительное число, то мы можем его отбросить, не изменяя знака неравенства, потому что отбросить BD — всё равно, что умножить на это число обе части неравенства. Отбросив BD, получим неравенство, не содержащее дробей:
AD — BС > 0.
Если BD — отрицательное число, то мы можем его отбросить, переменив при этом знак неравенства на противоположный; тогда снова будем иметь неравенство с целыми членами:
AD — BC < 0.
Но если знак BD неизвестен (что бывает вообще тогда, когда В и D содержат неизвестные), то мы не можем умножать обе части неравенства на BD. Тогда рассуждаем так: чтобы дробь была положительна, необходимо и достаточно, чтобы у неё числитель и знаменатель были одновременно или положительны, или отрицательны. Следовательно, неравенство (2) удовлетворится при таких значениях букв, при которых: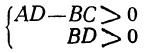 или
или 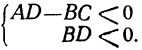
Таким образом, решение неравенства (1) сводится к решению системы двух неравенств без дробных членов.
Доказательство неравенства
Нельзя установить каких-либо общих правил для обнаружения верности предложенного неравенства. Заметим только, что один из приёмов состоит в том, что предложенное неравенство преобразовывают в другое — очевидное, и затем, исходя из этого очевидного неравенства, путём логических рассуждений доходят до предложенного. Приведём пример:
Доказать, что если сумма чисел х и у постоянна, то их произведение будет наибольшее, если х=у.
Пусть х+у = а, где а—постоянное число. Если х=у, то каждое из этих чисел будет 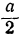 , и тогда ху сделается равным
, и тогда ху сделается равным 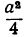 .
.
Требуется доказать, что если х ≠ у, то 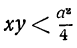 . Преобразуем это доказываемое неравенство так:
. Преобразуем это доказываемое неравенство так:
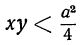 ; 4xy < a² ; 4xy < (х+у)² ; 4xy < x² +2xy+y² ;
; 4xy < a² ; 4xy < (х+у)² ; 4xy < x² +2xy+y² ;
0 < x² — 2xy+y² ; 0 < (х — у)² .
При неравных х и у последнее неравенство верно. Переходя от него последовательно к предыдущим неравенствам, замечаем, что все они равносильны. Значит, и первое неравенство верно.
Если, например, x + y=10, то наибольшая величина произведения есть 5∙5=25.
Решение неравенства первой степени с одним неизвестным
Общий вид неравенства первой степени с одним неизвестным, после раскрытия в нём скобок и освобождения от дробных членов, следующий:
ax + b> a₁x + b₁.
Перенеся неизвестные члены в левую часть, а известные в правую, получим:
(a— a₁ ) x> b₁ — b .
Если а — a₁ > 0, то, разделив на а — a ₁ обе части неравенства, найдём: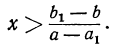
Если же а—a₁ < 0, то получим: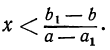
Таким образом, одно неравенство первой степени даёт для неизвестного один предел, ограничивающий значение неизвестного или сверху (x < m), или снизу (x > m).
Пример:
Решить неравенство: 2x(2x — 5) — 27 < (2x+1)² . Раскрываем скобки:
4x² — 10x — 27 < 4x² + 4x+ 1.
Переносим члены и делаем приведение:
— 14x<28.
Делим обе части на — 14:
х >— 2.
4x+ 1. Переносим члены и делаем приведение: — 14x<28. Делим обе части на — 14: х >— 2.
Два неравенства первой степени с одним неизвестным
Рассмотрим систему двух неравенств:
ax+b> a’x +b’ и cx+d> c’x + d’.
Каждое из этих неравенств даёт по одному пределу для неизвестного.
При этом могут представиться три случая:
- Пределы одинакового смысла; тогда для решения системы достаточно взять один из них. Если, например, х > 7 и х > 12, то достаточно взять только x > 12, потому что, если х > 12, то и подавно x >7, или если, например, х < 5 и х < 8, то достаточно положить, что x<5, потому что тогда и подавно x < 8.
- Пределы противоположного смысла, например х > 10 и х < 15. В этом случае для неизвестного можно брать только такие значения, которые заключены между найденными пределами.
- Пределы противоречат друг другу, например x < 5 и х >7. В этом случае система не имеет решений.
Пример:
Решить два неравенства: 0,3x + 5 < 0,5x и 5x < 60 +2x Первое неравенство даёт x>25, второе: x < 20. Значит, если эти неравенства выведены из условий одной и той же задачи, то эта задача не имеет решений.
Основные понятия, связанные с решением неравенств
Опыт проведения приемных экзаменов в вузы свидетельствует о том, что многие абитуриенты допускают ошибки при решении неравенств.
Если при решении уравнений можно использовать преобразования, приводящие к появлению посторонних корней, которые выявляются с помощью проверки, то при решении неравенств обычно нет возможности отсеять посторонние решения, так как множество решений неравенства, как правило, бесконечно.
Поэтому при решении неравенства нужно внимательно следить за тем, чтобы в процессе решения не менялось множество его решений, т. е. чтобы при каждом преобразовании неравенство заменялось равносильным.
Рассмотрим основные понятия, связанные с решением неравенств. Если на некотором множестве Е определены функции f(x) и g(x) и ставится задача решить неравенство
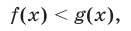
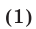
то это означает, что требуется найти все значения 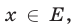 , при подстановке которых в неравенство (1) получается верное числовое неравенство.
, при подстановке которых в неравенство (1) получается верное числовое неравенство.
Каждое такое значение х называется решением неравенства, а совокупность всех решений — множеством решений этого неравенства.
Из этого определения следует, что каждое решение неравенства (1) принадлежит множеству, которое является пересечением (общей частью) областей определения функций f(x) и g(x) и называется областью допустимых значений (ОДЗ) неравенства (1).
Неравенство вида (1) называют строгим в отличие от неравенства
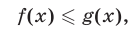
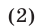
которое называют нестрогим.
Множество решений неравенства (2) можно получить, объединив множество решений неравенства (1) с множеством решений уравнения f(x) = g(x).
При решении неравенств, как и при решении уравнений, широко используется понятие равносильности.
Неравенство (1) и неравенство
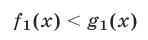

называют равносильными на множестве М, если множества решений этих неравенств совпадают, т. е. каждое решение неравенства (1), принадлежащее множеству М, является решением неравенства (3) и, обратно, каждое решение неравенства (3), принадлежащее множеству М, является решением неравенства (1). Если неравенства (1) и (3) не имеют решений, то эти неравенства считаются равносильны-
Сформулируем основные утверждения, связанные с понятием равносильности.
1°. Неравенства
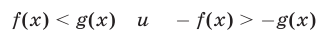
равносильны на любом числовом множестве.
2°. Если функции f(x), g(x) и h(x) определены на множестве М, то неравенства
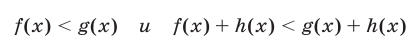 равносильны на множестве М.
равносильны на множестве М.
Например, неравенство
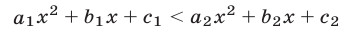
при любых  равносильно неравенству
равносильно неравенству
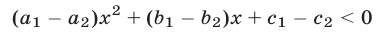
на множестве R.
3°. Если функции 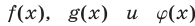 определены на множестве М и
определены на множестве М и  для всех
для всех 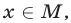 то неравенства
то неравенства
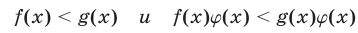
равносильны на множестве М.
Применяя утверждения 1° и 3° к линейным неравенствам, т. е. к неравенствам вида
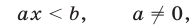
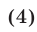
получаем:
а) если  то неравенство (4) равносильно неравенству
то неравенство (4) равносильно неравенству 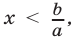 т. е. решениями неравенства (4) являются все числа из промежутка
т. е. решениями неравенства (4) являются все числа из промежутка 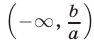 и только эти числа;
и только эти числа;
б) если 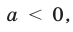 то неравенство (4) равносильно неравенству
то неравенство (4) равносильно неравенству 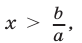 т.е. множество решений неравенства (4) — промежуток
т.е. множество решений неравенства (4) — промежуток 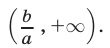
4°. Если 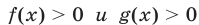 для всех
для всех 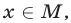 то неравенства
то неравенства
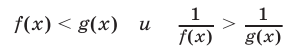
равносильны на множестве М.
5°. Если функции f(x) и g(x) определены на множестве М, то неравенство
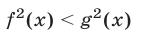
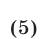
равносильно неравенству
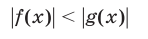
на этом множестве.
В случае, когда f(x) > 0 и g(x) > 0 для всех 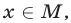 неравенство (5) равносильно неравенству f(x) < g(x).
неравенство (5) равносильно неравенству f(x) < g(x).
Например, неравенство 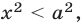 где
где 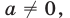 равносильно неравенству
равносильно неравенству 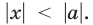 В частности, неравенство
В частности, неравенство 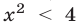 равносильно неравенству
равносильно неравенству 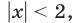 т. е. множество решений неравенства
т. е. множество решений неравенства 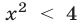 — это интервал
— это интервал 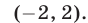
Для неравенств, как и для уравнений, вводятся понятия «система неравенств» и «совокупность неравенств».
Число  называется решением системы неравенств
называется решением системы неравенств
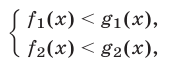
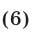
если это число является решением каждого неравенства системы (6). Пусть 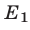 и
и 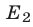 — множества решений соответственно первого и второго неравенств системы (6), тогда множество
— множества решений соответственно первого и второго неравенств системы (6), тогда множество 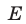 решений системы (6) является пересечением множеств
решений системы (6) является пересечением множеств 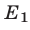 и
и 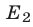 , т.е.
, т.е. 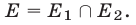
Число  называется решением совокупности неравенств
называется решением совокупности неравенств

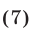
если это число является решением хотя бы одного из неравенств (7). Пусть 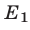 и
и 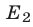 — множества решений соответственно первого и второго неравенства совокупности (7), тогда множество
— множества решений соответственно первого и второго неравенства совокупности (7), тогда множество 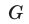 решений совокупности неравенств (7) является объединением множеств
решений совокупности неравенств (7) является объединением множеств 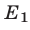 и
и 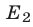 , т. е.
, т. е. 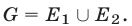
Понятие равносильности переносится на системы и совокупности неравенств. Говорят, что неравенство (1) равносильно системе неравенств (6), если это неравенство и система (6) имеют одни и те же решения или не имеют решений.
Неравенство (1) называют равносильным совокупности неравенств (7), если выполняются следующие условия:
1) каждое решение неравенства (1) является решением по крайней мере одного из неравенств (7);
2) любое решение каждого из неравенств (7) является решением неравенства (1).
При решении неравенств часто используются следующие утверждения.
6°. Неравенство
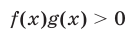
равносильно совокупности следующих двух систем неравенств:
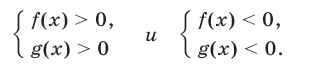
7°. Неравенство
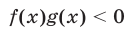
равносильно совокупности следующих двух систем неравенств:
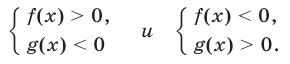
Примеры с решениями:
Пример:
Решить неравенство 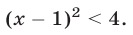
Решение:
Это неравенство равносильно следующему: 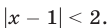 Так как модуль разности двух чисел равен расстоянию между точками, изображающими эти числа, то решение данного неравенства сводится к нахождению точек
Так как модуль разности двух чисел равен расстоянию между точками, изображающими эти числа, то решение данного неравенства сводится к нахождению точек 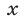 числовой прямой, которые удалены от точки 1 на расстояние, не превосходящее 2 (рис. 19.1). Такими точками являются точки интервала (—1,3).
числовой прямой, которые удалены от точки 1 на расстояние, не превосходящее 2 (рис. 19.1). Такими точками являются точки интервала (—1,3).
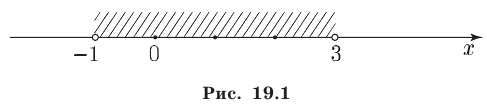
Ответ. — 1 < х < 3.
Пример:
Решить неравенство 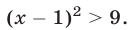
Решение:
Неравенству 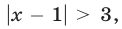 которое равносильно исходному, удовлетворяют все точки числовой прямой, расстояние от которых до точки 1 больше 3 (рис. 19.2).
которое равносильно исходному, удовлетворяют все точки числовой прямой, расстояние от которых до точки 1 больше 3 (рис. 19.2).
Это точки, лежащие вне отрезка длины 6 с центром в точке 1, т.е. точки, лежащие вне отрезка [-2,4]. Таким образом, множество решений исходного неравенства — объединение промежутков 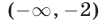 и
и 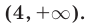
Ответ. х < -2, х > 4.

Пример:
Решить неравенство 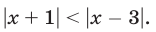
Решение:
Первый способ. Так как обе части неравенства неотрицательны, то при возведении их в квадрат получается равносильное неравенство
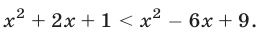
Это неравенство равносильно неравенству 8х < 8, откуда х < 1.
Ответ. х < 1.
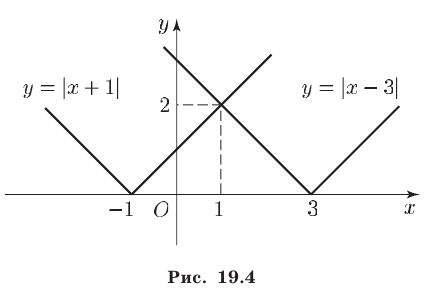
Второй способ. Решение данного неравенства сводится к нахождению точек х числовой прямой, которые расположены ближе к точке — 1, чем к точке 3 (рис. 19.3). Такими точками являются все точки, лежащие слева от точки 1 — середины отрезка [-1,3], т.е. точки из промежутка 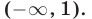
Третий способ. Построим графики функций 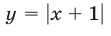 и
и 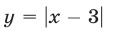 (рис. 19.4).
(рис. 19.4).
Эти графики пересекаются в точке (1;2). При х < 1 график функции у = |x+ 1| лежит ниже графика функции у = |х — 3|, а при х > 1 — выше. Поэтому множество решений данного неравенства — промежуток 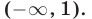
Пример:
Решить систему неравенств
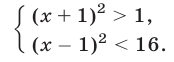
Решение:
Данная система равносильна следующей:
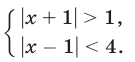
Множество 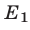 решений первого неравенства этой системы состоит из точек числовой прямой (рис. 19.5), лежащих вне отрезка [ — 2,0], т.е.
решений первого неравенства этой системы состоит из точек числовой прямой (рис. 19.5), лежащих вне отрезка [ — 2,0], т.е. 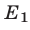 —объединение промежутков
—объединение промежутков  и
и 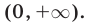
Множество 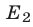 решений второго неравенства — интервал длины 8 с центром в точке 1 (рис. 19.5), т.е.
решений второго неравенства — интервал длины 8 с центром в точке 1 (рис. 19.5), т.е. 
Множество Е решений исходной системы — общая часть (пересечение) множеств 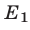 и
и 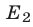 .
.

Следовательно, множество Е — объединение интервалов (-3,-2) и (0,5).
Ответ. —3 < x < -2, 0 < х < 5.
Пример:
Решить неравенство 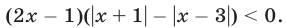
Решение:
Данное неравенство равносильно совокупности двух систем неравенств:
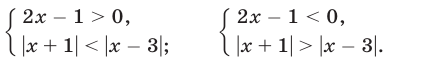
Множество 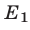 решений первой системы — пересечение промежутков
решений первой системы — пересечение промежутков 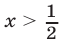 и
и 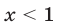 (см. пример 3), т. е.
(см. пример 3), т. е. 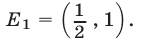
Множество 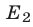 решений второй системы — пересечение промежутков
решений второй системы — пересечение промежутков 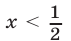 и
и  , не имеющих общих точек. Поэтому вторая система решений не имеет.
, не имеющих общих точек. Поэтому вторая система решений не имеет.
Ответ. 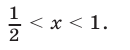
Пример:
Решить неравенство
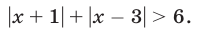
Решение:
Первый способ. Используя определение модуля, получаем
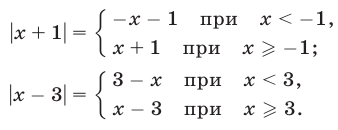
Пусть 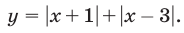 Тогда из соотношений (9) и (10) следует, что
Тогда из соотношений (9) и (10) следует, что

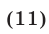
Поэтому неравенство (8) равносильно совокупности следующих систем неравенств:
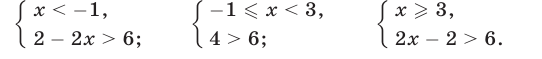
Множество 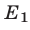 решений первой из этих систем — промежуток
решений первой из этих систем — промежуток  вторая система не имеет решений, а множество
вторая система не имеет решений, а множество 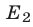 решений третьей системы — промежуток
решений третьей системы — промежуток 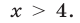 Следовательно, множество решений исходной системы — объединение множеств
Следовательно, множество решений исходной системы — объединение множеств 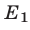 и
и 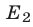 .
.
Ответ. 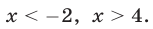
Второй способ. Решить неравенство (8) — значит найти все точки х числовой прямой, сумма расстояний от каждой из которых до точек —1 и 3 больше 6 (рис. 19.6).

Найдем точку 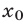 , где
, где 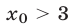 , такую, чтобы сумма
, такую, чтобы сумма 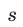 расстояний от точки
расстояний от точки 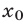 до точек —1 и 3 была равна 6. Если
до точек —1 и 3 была равна 6. Если 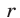 —расстояние от точки
—расстояние от точки 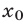 до точки 3, то
до точки 3, то 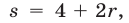 так как длина отрезка [—1,3] равна 4. Поэтому s = 6 при r = 1. Следовательно,
так как длина отрезка [—1,3] равна 4. Поэтому s = 6 при r = 1. Следовательно, 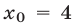 и все значения х такие, что
и все значения х такие, что 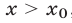 , являются решениями неравенства (8). Аналогично, решениями неравенства (8) являются значения х такие, что х < —2 (точки —2 и 4 расположены симметрично относительно точки 1 — середины отрезка [—1,3]).
, являются решениями неравенства (8). Аналогично, решениями неравенства (8) являются значения х такие, что х < —2 (точки —2 и 4 расположены симметрично относительно точки 1 — середины отрезка [—1,3]).
Третий способ. Используя соотношения (11), построим график функции 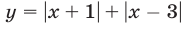 (рис. 19.7).
(рис. 19.7).
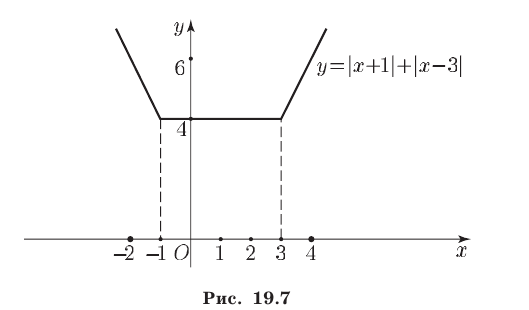
При х < -2 и при х > 4 график расположен выше прямой у = 6. Поэтому решениями неравенства (8) являются все х такие, что х < —2, а также все х такие, что х > 4.
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
Функциональные неравенства
Перейдем к изучению неравенств между функциями от одного или нескольких переменных. Задачи о таких неравенствах распадаются на два больших класса. В одних задачах требуется доказать, что в той или иной области, где заданы две функции, их значения удовлетворяют заданному неравенству. Мы будем говорить в этом случае, что неравенство выполняется в этой области тождественно. Такие задачи называют задачами на доказательство не равенств.
Иной вид имеют задачи второго типа. Здесь задано неравенство между функциями и надо найти все значения аргумента (или аргументов, если функции зависят от нескольких переменных), для которых это неравенство выполняется. Такие задачи мы будем называть задачами на решение неравенств.
Теория неравенств во многом напоминает теорию уравнений. Существенным отличием является то, что уравнение, как правило, имеет конечное множество решений. Решения же неравенств с одним неизвестным заполняют целые промежутки на числовой оси. Для неравенств со многими неизвестными мы получаем в качестве решений области на плоскости, в пространстве и т. д.
Понятия системы неравенств и совокупности неравенств определяются точно так же, как и для уравнений. Именно, мы будем говорить, что задана система неравенств
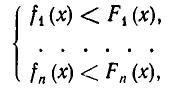
если надо найти все значения х, при которых выполняются в с е эти неравенства. Если же надо найти все значения х, при которых выполняется хоть одно из неравенств  то говорят, что задана совокупность неравенств (с одним неизвестным). Совокупность неравенств обозначают так:
то говорят, что задана совокупность неравенств (с одним неизвестным). Совокупность неравенств обозначают так:
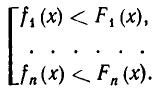
Рассмотрим сначала некоторые общие вопросы теории функциональных неравенств.
Следствия из неравенств
Пусть дана система неравенств

Мы будем говорить, что неравенство

является следствием системы неравенств (1), если оно имеет место для любого х, удовлетворяющего всем неравенствам (1). Иными словами, если выполняются все неравенства (1), то должно выполняться и их следствие (2 ).
Это определение можно сформулировать следующим образом. Обозначим через  множество точек, в которых выполняется неравенство
множество точек, в которых выполняется неравенство 
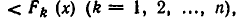 а через М — множество точек, где выполняется неравенство (2). Неравенство (2) является следствием системы неравенств (1), если М содержит пересечение всех множеств
а через М — множество точек, где выполняется неравенство (2). Неравенство (2) является следствием системы неравенств (1), если М содержит пересечение всех множеств 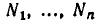
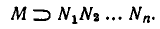
В самом деле, пересечение множеств 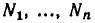 состоит из чисел, удовлетворяющих всем неравенствам (1). Поэтому если (2) — следствие системы неравенств (1), то оно выполняется во всех точках этого пересечения. А это и означает, что
состоит из чисел, удовлетворяющих всем неравенствам (1). Поэтому если (2) — следствие системы неравенств (1), то оно выполняется во всех точках этого пересечения. А это и означает, что 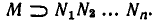
Чаще всего приходится пользоваться следующими утверждения ми о следствиях из неравенств.
Теорема:
Если на некотором множестве А выполняются неравенства

и

то на А имеет место и неравенство
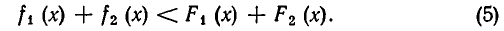
Доказательство. Пусть а — число из множества А. Тогда справедливы числовые неравенства

Следовательно, имеет место неравенство:
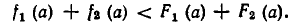
Оно показывает, что при 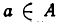 выполняется неравенство (5). Значит, (5) является следствием из (3) и (4).
выполняется неравенство (5). Значит, (5) является следствием из (3) и (4).
Точно так же доказывается следующая
Теорема:
Пусть на некотором множестве А выполняются неравенства
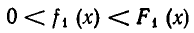
и
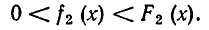
Тогда на этом множестве имеет место и неравенство

Равносильные неравенства
Введем следующее определение.
Определение:
Два неравенства

и

называются равносильными, если каждое число, удовлетворяющее неравенству (1), удовлетворяет и неравенству (2), а каждое число, удовлетворяющее (2), удовлетворяет и (1) (в частности, если множества решений обоих неравенств пусты).
Иными словами, два неравенства равносильны, если каждое из них является следствием другого.
Для установления равносильности двух неравенств применяются следующие теоремы.
Теорема:
Пусть функция 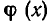 определена при всех допустимых значениях х. Тогда неравенства
определена при всех допустимых значениях х. Тогда неравенства

и
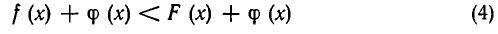
равносильны.
Для доказательства этой теоремы достаточно заметить, что из f (а)<F(а) следует
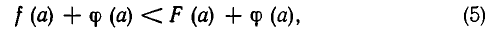
а из (5) следует f(а)<F(а).
Из теоремы 1 вытекает следующее правило переноса членов в неравенствах:
Неравенства
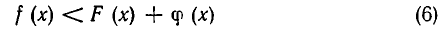
и
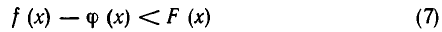
равносильны.
В самом деле, (6) получается из (7) прибавлением к обеим частям функции — 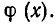
Из этого следствия вытекает, что любое неравенство f(х)<F(х) равносильно неравенству вида F(х) —f(х) >0 .
Точно так же доказывается следующая
Теорема:
Неравенства

и

равносильны. Равносильны и неравенства

и

Наконец, докажем следующую теорему.
Теорема:
Пусть функция ср (х) определена при всех допустимых значениях х и положительна. Тогда неравенства

и
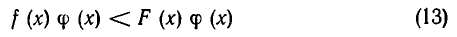
равносильны.
Доказательство. Пусть а — число, удовлетворяющее неравенству (12): f(а)<F(а). Умножим обе части этого неравенства на 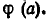 Так как
Так как 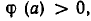 то знак неравенства не изменится. Мы получим
то знак неравенства не изменится. Мы получим
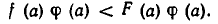
Это показывает, что а удовлетворяет неравенству (13), а потому (13) является следствием (12). Точно так же доказывается, что (12) является следствием (13). Для этого достаточно умножить обе части неравенства (13) на положительное число 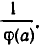
Если же функция ф (а) определена для всех допустимых значений х и отрицательна, то неравенство f(x)<F (х) равносильно неравенству
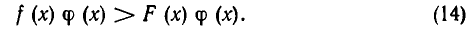
В общем случае приходится разбивать множество допустимых значений на три подмножества: точек х , где 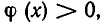 точек х, где
точек х, где 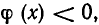 и точек х, где
и точек х, где 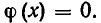
Мы доказывали теоремы о равносильности для неравенства с одним переменным. Эти теоремы остаются верными и для неравенств с несколькими переменными.
Доказательство неравенств
Для доказательства неравенств применяют один из следующих двух путей.
1) Исходят из неравенства, которое надо доказать, и последовательно заменяют его равносильными неравенствами, пока не дойдут до очевидного неравенства. Так как на каждом шагу получалось неравенство, равносильное данному, то тем самым справедливость данного неравенства доказана.
2) Исходят из какого-нибудь очевидного неравенства и заменяют его неравенствами-следствиями до тех пор, пока не придут к доказываемому неравенству. Мы знаем, что неравенство 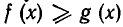 равносильно неравенству
равносильно неравенству 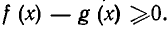 Поэтому доказательство неравенства
Поэтому доказательство неравенства 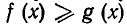 сводится к доказательству того, что разность левой и правой частей неравенства положительна. Для этого стараются представить эту разность в виде суммы или произведения заведомо положительных выражений.
сводится к доказательству того, что разность левой и правой частей неравенства положительна. Для этого стараются представить эту разность в виде суммы или произведения заведомо положительных выражений.
Рассмотрим следующий пример. Доказать неравенство
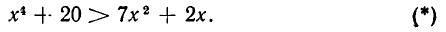
Это неравенство равносильно неравенству
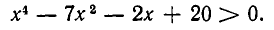
Перепишем левую часть в виде
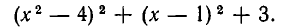
Так как, очевидно 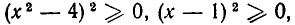 то неравенство (*) доказано.
то неравенство (*) доказано.
Далее докажем, что дробь 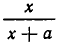 , где х > 0, а >0, увеличивается, если к числителю и знаменателю прибавить одно и то же положительное число b. Иными словами, докажем, что при х > 0, а > 0, b > 0 выполняется неравенство
, где х > 0, а >0, увеличивается, если к числителю и знаменателю прибавить одно и то же положительное число b. Иными словами, докажем, что при х > 0, а > 0, b > 0 выполняется неравенство

Для этого составим разность левой и правой частей неравенства:
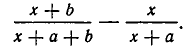
Приведя дробит к одному знаменателю, получаем:
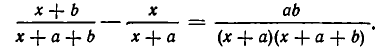
Так как правая часть этого равенства заведомо положительна, то неравенство (**) доказано.
Теперь приведем пример на использование второго способа доказательства неравенства. Докажем, что для любого действительного числа х имеет место неравенство

причем знак равенства получается лишь при х =1 .
Будем исходить из очевидного неравенства

имеющего место при любом действительном х, причем равенство в формуле (2) может иметь место лишь при х = 1 .
Раскроем скобки в выражении (2). Мы получим неравенство 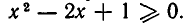 Но при любом значении х можно прибавить к обеим частям неравенства число 2х, а потом разделить обе части полученного неравенства на 2 (см. п. 2). Выполнив эти операции,
Но при любом значении х можно прибавить к обеим частям неравенства число 2х, а потом разделить обе части полученного неравенства на 2 (см. п. 2). Выполнив эти операции,
получаем доказываемое неравенство (1), где знак равенства имеет место лишь при х = 1 .
Линейные неравенства
Перейдем теперь к методам решения неравенств. Начнем с простейшего случая — линейного неравенства с одним неизвестным. Такое неравенство имеет вид ах+ b > 0 или ах+b<0.
Если а =0, то неравенство принимает вид b >0. В случае, когда b — положительное число, это неравенство справедливо для всех значений х, а в случае, когда b — отрицательное число, оно не имеет места ни при одном значении х.
Рассмотрим более интересный случай, когда 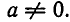 Не теряя общности, можно считать, что а > 0. Если а<0, то обе части неравенства умножим н а—1 , изменив знак неравенства на противоположный (например, неравенство — Зх+8>0 можно заменить равносильным неравенством Зх — 8<0).
Не теряя общности, можно считать, что а > 0. Если а<0, то обе части неравенства умножим н а—1 , изменив знак неравенства на противоположный (например, неравенство — Зх+8>0 можно заменить равносильным неравенством Зх — 8<0).
Прибавим к обеим частям неравенства ах+b>0 число (—b). Мы получим равносильное неравенство ах >—b. Далее, разделив обе части неравенства ах > —b на а, получим неравенство 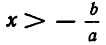 (напомним, что мы условились считать а положительным числом).
(напомним, что мы условились считать а положительным числом).
Итак, неравенство ах +b >0, где а — положительное число, равносильно неравенству 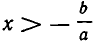 . Точно так же неравенство ах+b<0 равносильно неравенству
. Точно так же неравенство ах+b<0 равносильно неравенству 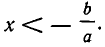
Полученный результат допускает простое геометрическое истолкование. Рассмотрим функцию у =ах+6 , а >0. Ее графиком является прямая линия, образующая острый угол с осью Ох и пересекающая эту ось в точке 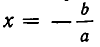 (см. (рис. 9).
(см. (рис. 9).
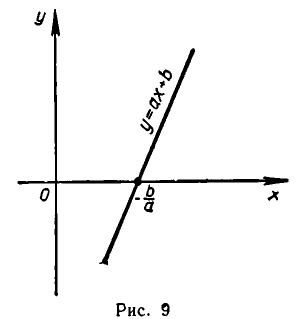
Ясно, что слева от точки — 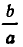 функция у = ах +b отрицательна, а справа от этой точки — положительна.
функция у = ах +b отрицательна, а справа от этой точки — положительна.
К неравенствам рассмотренного вида сводится решение более общих неравенств

В самом деле, неравенство (1) равносильно

К решению линейных неравенств сводится решение систем и совокупностей линейных неравенств. Чтобы найти решение систем линейных неравенств, надо решить каждое из них, а потом взять пересечение получившихся множеств. При решении совокупности линейных неравенств надо решить каждое из них и взять сумму получившихся множеств.
Пример:
Решить систему неравенств:
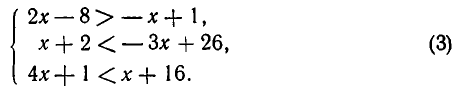
Решением первого из них является x > 3, второго х < 6 , а третьего х < 5. Ясно, что пересечением этих трех множеств является промежуток 3 < х < 5.
Пример:
Решить совокупность систем неравенств:
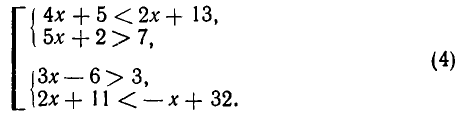
Сначала решим систему неравенств:
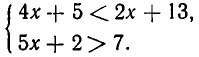
Так же, как и в примере 1, получаем промежуток 1<х<4.
Точно так же решением системы неравенств:
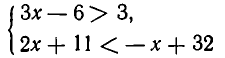
является промежуток 3<х<7. Решение совокупности (4) получается объединением этих промежутков. В результате получаем промежуток 1<х<7.
Решение неравенств второй степени
Перейдем теперь к решению квадратных неравенств, то есть неравенств вида
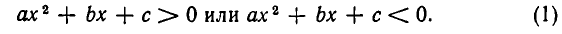
Мы можем, не теряя общности, считать, что а > 0.
Мы покажем сейчас, что решение неравенств второй степени сводится по сути дела к решению квадратных уравнений. При этом возможны различные случаи, в зависимости от знака дискриминанта 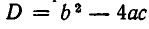 квадратного уравнения
квадратного уравнения
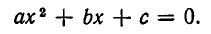
а) Пусть D > 0. В этом случае, как мы знаем, квадратное уравнение (2) имеет два различных действительных корня 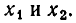 Будем считать, что
Будем считать, что  Имеет место соотношение
Имеет место соотношение
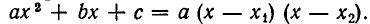
Значит, неравенство 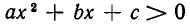 равносильно неравенству
равносильно неравенству
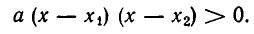
Сомножитель  положителен при
положителен при  и отрицателен при
и отрицателен при  , сомножитель
, сомножитель  положителен при
положителен при 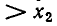 и отрицателен при
и отрицателен при  Иными словами, первый сомножитель меняет знак лишь при переходе через точку
Иными словами, первый сомножитель меняет знак лишь при переходе через точку 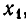 а второй — лишь при переходе через точку
а второй — лишь при переходе через точку 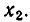 Поэтому произведение
Поэтому произведение 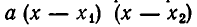 меняет знак лишь при переходе через одну из этих точек.
меняет знак лишь при переходе через одну из этих точек.
Иными словами, на каждом из промежутков
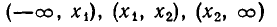
квадратный трехчлен 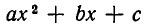 имеет постоянный знак.
имеет постоянный знак.
Легко найти, какой именно знак имеет трехчлен на каждом промежутке. Если 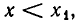 то тем более
то тем более  а потому оба сомножителя
а потому оба сомножителя 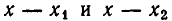 отрицательны. Но тогда их произведение
отрицательны. Но тогда их произведение 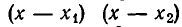 положительно. Поскольку мы предположили, что и а > 0 , то получаем: при
положительно. Поскольку мы предположили, что и а > 0 , то получаем: при  квадратный трехчлен
квадратный трехчлен 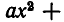
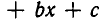 положителен. При переходе через точку
положителен. При переходе через точку 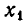 сомножитель
сомножитель 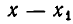 становится положительным, а сомножитель
становится положительным, а сомножитель  остается отрицательным. Значит, на промежутке
остается отрицательным. Значит, на промежутке 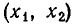 квадратный трехчлен
квадратный трехчлен 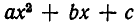 принимает отрицательные значения. Наконец, при
принимает отрицательные значения. Наконец, при  оба сомножителя
оба сомножителя 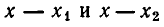 положительны, и по тому выполняется неравенство
положительны, и по тому выполняется неравенство
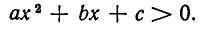
Итак, мы доказали следующее утверждение: если квадратный трехчлен 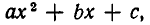 где а > 0, имеет два различных действительных корня
где а > 0, имеет два различных действительных корня 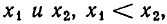 то неравенство
то неравенство 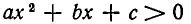 выполняется на промежутках
выполняется на промежутках 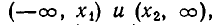 а неравенство
а неравенство 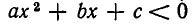 — на промежутке
— на промежутке 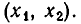
б) Пусть D = 0. В этом случае квадратный трехчлен 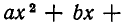
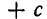 имеет два совпадающих корня
имеет два совпадающих корня 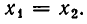 Следовательно, его можно записать в виде
Следовательно, его можно записать в виде
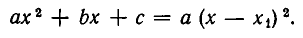
Но 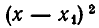 положительно при
положительно при 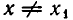 и равно нулю при
и равно нулю при 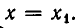 Итак, при а > 0 и D =0 неравенство
Итак, при а > 0 и D =0 неравенство 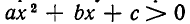 выполняется на промежутках
выполняется на промежутках 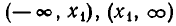 (то есть на всей числовой прямой с «выколотой» точкой
(то есть на всей числовой прямой с «выколотой» точкой 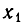 ), а неравенство
), а неравенство 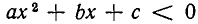 не выполняется ни в одной точке числовой оси.
не выполняется ни в одной точке числовой оси.
в) Наконец, рассмотрим случай, когда D < 0 .
Перепишем трехчлен 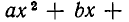
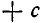 в виде:
в виде:
По условию имеем  Так как а > 0, то для всех значений х трехчлен
Так как а > 0, то для всех значений х трехчлен 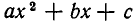 является суммой двух положительных слагаемых
является суммой двух положительных слагаемых 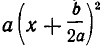 и
и 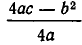 и потому положителен при всех значениях х.
и потому положителен при всех значениях х.
Итак, если D< 0, а >0, то неравенство 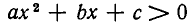 выполняется для всех значений х, а неравенство
выполняется для всех значений х, а неравенство 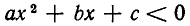 не выполняется ни для одного значения х.
не выполняется ни для одного значения х.
Полученные результаты допуска ют простое геометрическое истолкование. Рассмотрим функцию 
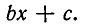 При а>0 графиком этой функции является парабола с осью, параллельной оси Оу, обращенная ветвями вверх.
При а>0 графиком этой функции является парабола с осью, параллельной оси Оу, обращенная ветвями вверх.
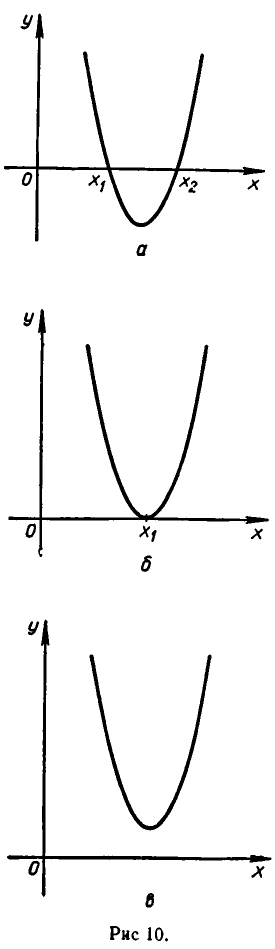
Если В > 0, то эта парабола пересекает ось в двух точках 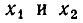 (рис. 10, а). Ясно, что заключенная между этими точками часть параболы лежит ниже оси Ох, а слева от
(рис. 10, а). Ясно, что заключенная между этими точками часть параболы лежит ниже оси Ох, а слева от 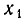 и справа от
и справа от 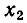 парабола лежит выше оси Ох.
парабола лежит выше оси Ох.
Если D = 0, то парабола касается оси Ох в некоторой точке 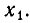 Слева и справа от этой точки она лежит выше Ох (рис. 10, б).
Слева и справа от этой точки она лежит выше Ох (рис. 10, б).
Наконец, при D<0, а > 0 парабола не пересекает оси Ох и расположена выше нее. Поэтому для всех значений х выполняется неравенство 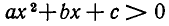 (рис. 10, б).
(рис. 10, б).
К неравенствам второй степени сводятся неравенства вида
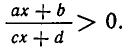
Умножив обе части неравенства на 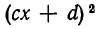 , получим равносильное неравенство второй степени:
, получим равносильное неравенство второй степени:
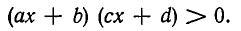
Пример:
Решить неравенство
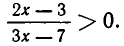
Это неравенство равносильно неравенству
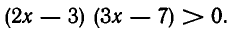
Корнями функции (2х — 3) (Зх — 7) являются числа 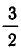 и
и 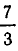 . Они разбивают ось на промежутки
. Они разбивают ось на промежутки 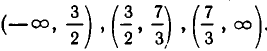 Выясняя знак 2х — 3 и Зх — 7 на этих промежутках, устанавливаем, что ответ имеет вид:
Выясняя знак 2х — 3 и Зх — 7 на этих промежутках, устанавливаем, что ответ имеет вид:
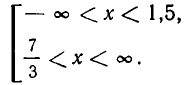
Приведем пример задачи, сводящейся к решению квадратных неравенств.
Задача:
Лодка спускается по течению реки на расстояние 10 км, а затем поднимается против течения на расстояние 6 км. Скорость течения реки равна 1 км/ч. В каких пределах должна лежать собственная скорость лодки, чтобы вся поездка заняла от 3 до 4 часов?
Решение. Пусть v — собственная скорость лодки. Тогда ее скорость по течению реки равна v + 1, а против течения реки равна v — 1. Поэтому время движения лодки равно
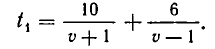
По условию имеем:
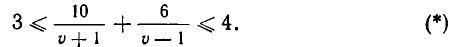
Должно выполняться неравенство v > 1 , так как иначе лодка не смогла бы идти против течения. Поэтому неравенство (*) равносильно неравенству
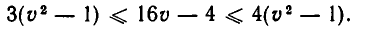
Итак, мы получили систему неравенств
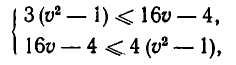
то есть систему неравенств
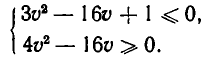
Корнями_ уравнения  являются числа
являются числа 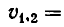
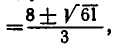 а уравнения
а уравнения 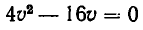 — числа
— числа 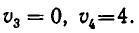 Первое неравенство выполняется на отрезке
Первое неравенство выполняется на отрезке 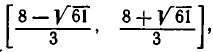 а второе —при условии
а второе —при условии 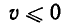 или
или 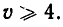 Но мы знаем, что
Но мы знаем, что 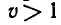 . Поэтому получаем систему неравенств:
. Поэтому получаем систему неравенств:
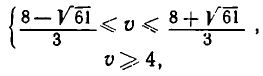
из которой окончательно получаем:
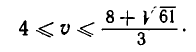
Решение алгебраических неравенств высших степеней
Мы видели, что решение квадратичного неравенства свелось по сути дела к решению квадратного уравнения. Корни 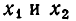 этого уравнения разбивали числовую ось на промежутки, где квадратный трехчлен сохранял постоянный знак. После этого было достаточно отобрать те промежутки, где выполняется требуемое неравенство.
этого уравнения разбивали числовую ось на промежутки, где квадратный трехчлен сохранял постоянный знак. После этого было достаточно отобрать те промежутки, где выполняется требуемое неравенство.
Точно так же решение неравенства вида
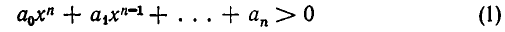
сводится к решению алгебраического уравнения
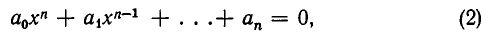
точнее говоря, к отысканию действительных корней этого уравнения. Чтобы осуществить это сведение, нам понадобится следующее утверждение, которое будет доказано в главе V (см. стр. 238): любой многочлен с действительными коэффициентами разлагается на множители первой и второй степеней, причем множители второй степени не имеют действительных корней.
Поэтому неравенство (1) можно записать так:
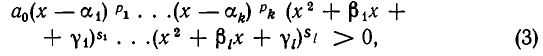
где множители
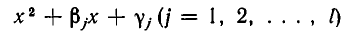
не имеют действительных корней и потому положительны на всей числовой оси (см. п. 2). Поэтому, отбрасывая эти множители, мы приходим к равносильному неравенству
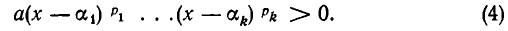
А теперь заметим, что множитель  отрицателен при
отрицателен при 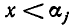 и положителен при
и положителен при 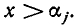 Иными словами, этот множитель меняет знак лишь при переходе через точку а Значит, если расположить действительные корни
Иными словами, этот множитель меняет знак лишь при переходе через точку а Значит, если расположить действительные корни  многочлена
многочлена
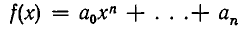
в порядке возрастания, то на промежутках
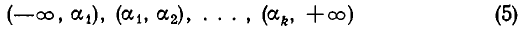
многочлен f(х) сохраняет постоянный знак. Поэтому достаточно выбрать на каждом из промежутков (5) «пробную точку» и найти знак многочлена f(х) в этой точке. Тот же знак многочлен будет иметь и на всем промежутке. Вместо подсчета значения в «пробной точке» можно подсчитать число положительных и отрицательных сомножителей в разложении (4).
Совокупность промежутков, на которых f(х) принимает положительные значения, дает решение неравенства f(х) >0 , а совокупность промежутков, в которых f(х) принимает отрицательные значения — решение неравенства f(х)<0 .
Пример:
Решить неравенство
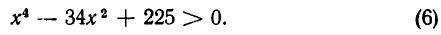
Найдем сначала корни уравнения
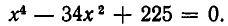
Это биквадратное уравнение. Решая его, получаем корни:
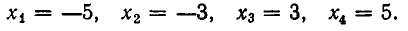
Найденные корни разбивают действительную ось на промежутки
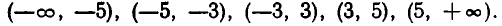
На промежутке 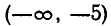 выберем «пробную точку»—6 , на промежутке (—5, —3) — точку —4, на промежутке (—3, 3) — точку 0, на (3, 5) — точку 4 и на
выберем «пробную точку»—6 , на промежутке (—5, —3) — точку —4, на промежутке (—3, 3) — точку 0, на (3, 5) — точку 4 и на 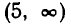 — точку 6 . Мы имеем:
— точку 6 . Мы имеем:
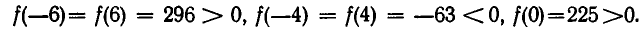
Отсюда вытекает, что решение неравенства (4) состоит из промежутков 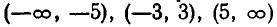 . Это решение можно записать так:
. Это решение можно записать так:
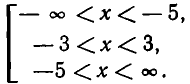
Неравенства вида
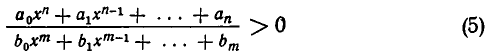
решаются точно так же. Именно, умножим числитель и знаменатель на один и тот же множитель 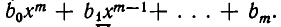 Тогда знаменатель станет неотрицательным. Поэтому неравенство (5) равносильно неравенству
Тогда знаменатель станет неотрицательным. Поэтому неравенство (5) равносильно неравенству
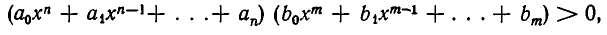
которое решается описанным выше образом.
Пример:
Решить неравенство

Это неравенство равносильно следующему:
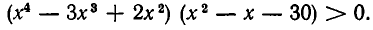
Решая уравнения
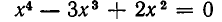
и
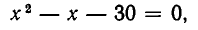
находим их корни: 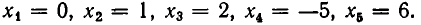
Расположим эти корни в порядке возрастания. Полученные числа разбивают действительную ось на промежутки:
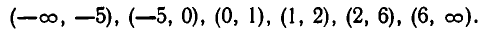
Методом «пробных точек» находим, что решение неравенства (6) состоит из промежутков:
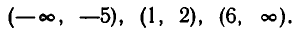
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

