Оглавление:
При решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции y=f(x) получать новую функцию, которую называют производной функцией (или просто производной) данной функции f(x)
Производная
Пусть функция у = f(х) определена на интервале (а, b). Возьмем какое-нибудь значение х из этого интервала. Затем возьмем другое новое значение аргумента х + ∆х, придав первоначальному значению х прирашение ∆х, положительное или отрицательное, но такое, чтобы точка х + ∆х содержалась в интервале (а, b). Найдем прирашение функции ∆у, отвечающее приращению ∆х аргумента:
∆у = f(x + ∆х) — f(x).
Составим разностное отношение приращения функции ∆у к соответствующему приращению ∆х ≠ 0 аргумента:
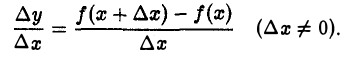
При фиксированном х это отношение является функцией от ∆х:
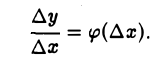
Определение:
Если при ∆х → 0 существует предел отношения 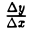 то этот предел называется производной от функции у = f(x) в данной точке х и обозначается f'(х) или у'(х) или у’х.
то этот предел называется производной от функции у = f(x) в данной точке х и обозначается f'(х) или у'(х) или у’х.
Таким образом, по определению (1)
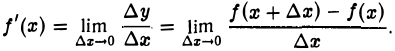
Примеры:
- Пусть у = x2. Тогда в любой точке х для любого ∆х имеем
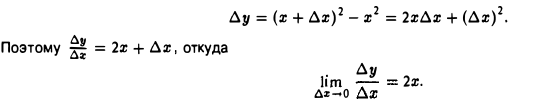
Но 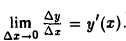 Следовательно, функция у = х2 имеет во всякой точке х производную у’ = 2х,
Следовательно, функция у = х2 имеет во всякой точке х производную у’ = 2х,
т. е.
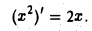
Пусть у = еx. Тогда в любой точке х для любого ∆х имеем
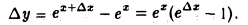
Отсюда
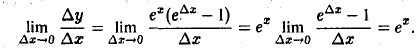
Таким образом,
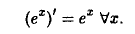
Замечание:
Формулу (I), определяющую производную функции f(х) бывает удобно брать в следующей эквивалентной форме. Пусть функция f(x) определена в точке xo и некоторой ее окрестности. Тогда
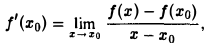
если этот предел существует.
Определение:
Будем говорить, что функция f(х) имеет производную на интервале (а, b), если производная f'(x) существует в каждой точке х ∈ (а, b).
Задача:
Для функции
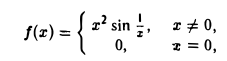
пользуясь определением производной, найти f'(0).
Задача:
Исходя из определения производной, доказать, что если периодическая с периодом Т функция f(x) имеет производную, то эта производная есть также Т-периодическая функция.
Задача:
Исходя из определения производной, доказать, что производная четной функции, имеющей производную, есть функция нечетная, а производная нечетной функции есть функция четная.
Геометрический смысл производной
Рассмотрим график функции у = f(х), непрерывной на интервале (а, b). Фиксируем произвольную точку М(х, f(х)) кривой у = f(х). Пусть Р{х + ∆х, f(х + ∆х)) — другая точка этой кривой. Проведем секущую MP (рис. 1). Касательной к кривой у = f(х) в точке М назовем прямую МТ, проходящую через точку М и являющуюся предельным положением секущей MP при стремлении точки Р к точке М по кривой (или, что то же, при ∆х —» 0). Это предельное положение секущей определяется тем, что угол ТМР стремится к нулю, когда точка Р стремится к точке М. Из рисунка видно, что угловой коэффициент kс секущей MP равен
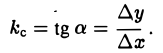
Пусть 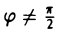 — угол, образуемый касательной МТ с осью Ох. Учитывая, что угловой коэффициент касательной МТ к кривой у = f(x) в точке М есть предел углового коэффициента секущей MP, когда точка Р стремится по кривой к точке М (и, значит, ∆х —» 0), получим
— угол, образуемый касательной МТ с осью Ох. Учитывая, что угловой коэффициент касательной МТ к кривой у = f(x) в точке М есть предел углового коэффициента секущей MP, когда точка Р стремится по кривой к точке М (и, значит, ∆х —» 0), получим
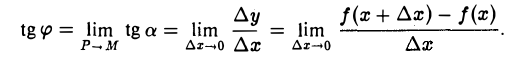
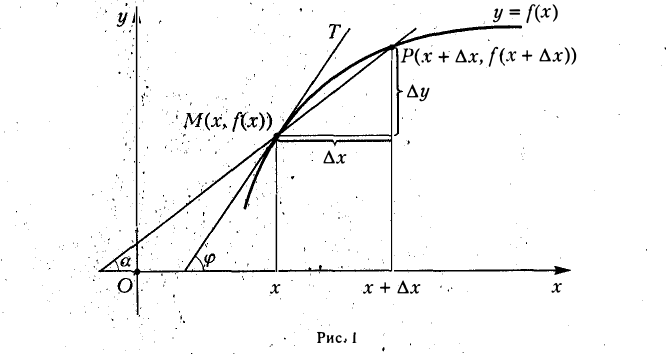
Последний предел (если он существует) есть производная f'(x), так что
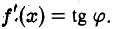
Таким образом, производная f'(x) функции у = f(x) есть угловой коэффициент kт касательной, проведенной к кривой у(х) = f(x) в точке с абсциссой х.
Уравнение касательной и нормали к кривой
Пусть имеем кривую, заданную уравнением у = f(x). Возьмем на этой кривой точку M0(x0, f(x0)) и выведем уравнение касательной к кривой в точке Мо, предполагая, что существует производная f'(x0).
Уравнение прямой с угловым коэффициентом к, проходящей через точку Mo(xo, уо), выглядит так
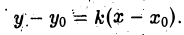
Угловой коэффициент касательной kr = f'(xо),поэтому уравнение касательной к кривой у = f(x) в точке Мо имеет вид
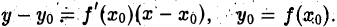
Нормалью к кривой в данной ее точке называется прямая, проходящая через эту точку перпендикулярно касательной к кривой в этой точке. Из определения нормали следует, что ее угловой коэффициент kn, связан с угловым коэффициентом kr касательной соотношением
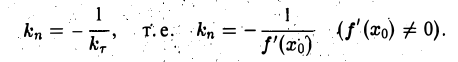
Уравнение нормали к кривой у = f(x) в точке Мо(xо, yо)’.
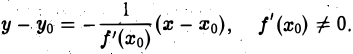
В случае, когда f'(x0) = 0, уравнение нормали есть x = x0.
Пример:
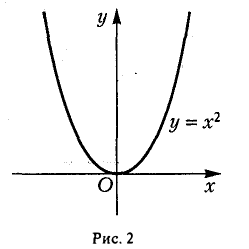
Написать уравнение касательной и нормали к кривой у = х2 в точке O(0,0).
Имеем f(х) = х2, f'(x) = 2х, f'(0) = 0. Поэтому уравнение касательной:
у — 0 = 0 • (х — 0) или у = 0 (ось Ох),
уравнение нормали:
z = 0 (ось Оу)
(рис.2).
Производная с точки зрения механики
Пусть S = S(t) — закон прямолинейного движения материальной точки, выражающий путь S, пройденный точкой, как функцию времени. Обозначим через ∆S путь, пройденный точкой за промежуток времени ∆t от момента t до t + ∆t, т. е.
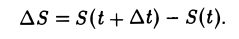
Отношение 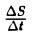 называется средней скоростью точки за время от t до t+ ∆t. Скорость v в данный момент t определим как предел средней скорости за промежуток времени от t до t + ∆t, когда ∆t → 0:
называется средней скоростью точки за время от t до t+ ∆t. Скорость v в данный момент t определим как предел средней скорости за промежуток времени от t до t + ∆t, когда ∆t → 0:
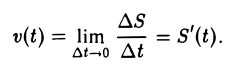
Таким образом, скорость v(t) есть производная от пути S = S(t) по времени t: v(t) = S'(t).
Пример:
Точка движется прямолинейно по закону S = t1 (S — метры, t — секунды). Найти ее скорость в момент t = 3.
Скорость точки в любой момент времени t
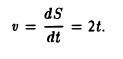
Отсюда 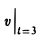 = 6 м/сек.
= 6 м/сек.
Правая и левая производные
Введем понятия правой и левой производной функции f(х) в точке х.
Определение:
Правой производной f'(х + 0) функции у = f(x) в данной точке ж называется величина
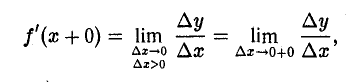
и левой производной f'(х — 0) — величина
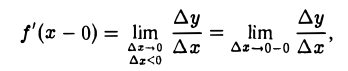
если указанные пределы существуют.
Пользуясь понятием односторонних пределов функции, получаем: для того чтобы в точке х существовала производная f'(x), необходимо и достаточно, чтобы в точке х функция у =f(x) имела правую и левую производные и эти производные были равны между собой:
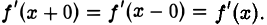
Следующий пример показывает, что существуют функции, которые имеют в точке х правую и левую производные, но не имеют производной в этой точке.
Пример:
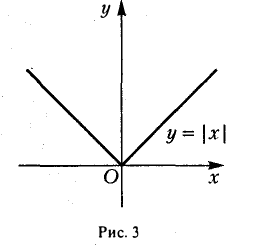
Рассмотрим функцию f(x) = |z|. Для этой функции отношение
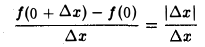
равно 1, если ∆х > 0, и равно -1, если ∆х < 0. Поэтому функция f(х) = |z| в точке 1=0 имеет правую производную
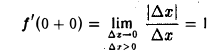
и левую производную
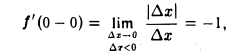
но они не равны, и значит, в точке х = 0 функция f(х) = |z| не имеет
производной. Геометрически это означает, что в точке O(0,0) график функции у = |z| (рис. 3) не имеет касательной.
Пусть функция f(x) непрерывна в точке х0. Будем говорить, что функция f{х) имеет в точке х0 бесконечную производную, равную + ∞ или — ∞, если в этой точке
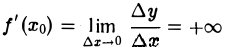
или соответственно
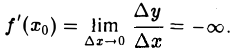
Геометрически это означает, что касательная к кривой у = f(x) в точке (хо, f(хо)) перпендикулярна к оси Ох.
Пример:
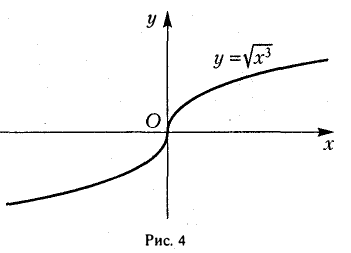
Рассмотрим, например, функцию f(x) = 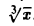 . Для этой функции при х = 0 имеем
. Для этой функции при х = 0 имеем
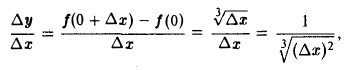
откуда видно, что 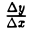 стремится к + ∞ при стремлении ∆х к нулю произвольным образом. График функции у =
стремится к + ∞ при стремлении ∆х к нулю произвольным образом. График функции у = 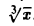 в точке O(0,0) имеет вертикальную касательную х = 0 (ось О у, рис. 4).
в точке O(0,0) имеет вертикальную касательную х = 0 (ось О у, рис. 4).
Таким образом, если функция у = f(x) в точке хо имеет конечную производную f'(хо), то в точке М0(х0, f(хо)) график функции у = f(x) имеет касательную (рис. 5), определяемую уравнением
y ~ f(xo) = f'(x0)(х — х0).
Определение:
Функция у = f(x) называется гладкой на интервале (а, b), если она непрерывна вместе со своей производной на этом интервале. В этом случае кривую, задаваемую правилом у = f(х), называют гладкой кривой на (а, b).
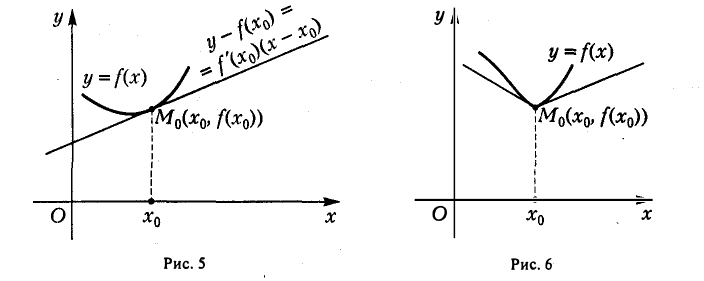
Если в точке хо функция у = f(х) непрерывна и имеет правую и левую производные f'(х0 +0) и f'(х0 — 0), причем f'(хо + 0) ≠ f'(х0 — 0), то в точке Af0(x0, f(х0)) график функции у = f(х) касательной не имеет (кривая не гладкая). Но существуют две односторонние полукасательные (рис.6). Точку Mq(xo, f(xо)) называют в этом случае угловой тонкой кривой у = f(x). Так, точка O(0,0) есть угловая точка графика функции у = |x|.
Если функция у = f(х) непрерывна в точке х0, а ее производная в точке Хо бесконечна, то возможны случаи:
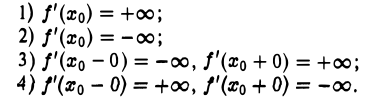
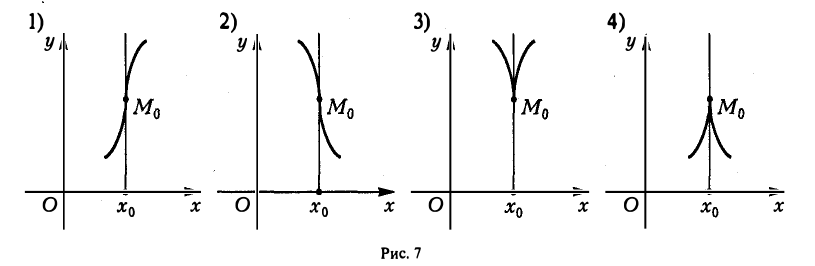
На рис. 7 представлены расположения касательной х = хо к графику функции у = f(х) в точке М0(х0, /(х0)), отвечающие случаям 1)-4). (В случаях 3) и 4) иногда говорят, что график функции у = f(х) имеет две слившиеся полукасательные.)
Дифференцируемость функции. Дифференциал функции
Пусть функция у = f(х) определена на интервале (а, b). Возьмем некоторое значение х ∈ (а, b). Дадим х приращение ∆х любое, но такое, чтобы х + ∆х ∈ (а, b). Тогда функция у = f(x) получит приращение
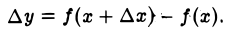
Определение. Функция у = f(х) называется дифференцируемой в точке х ∈ (а, b), если приращение функции
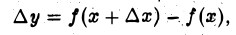
отвечающее приращению ∆х аргумента, можно представить в виде

где А — некоторое число, которое не зависит от ∆х (но, вообще говоря, зависит от х), а а( ∆х) → 0 при ∆х → 0. ‘
Пример:
Рассмотрим функцию у = х2. Во всякой точке х и при любом ∆х имеем
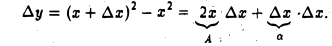
Отсюда, в силу определения, функция у = х2 дифференцируема в любой точке х, причем А = 2х, а(∆х) = ∆х.
Следующая теорема выражает необходимое и достаточное условие дифференци-руемости функции.
Теорема:
Для того чтобы функция у = f(х) была дифференцируемой в точке х, необходимо и достаточно, чтобы f(x) в этой точке имела конечную производную f'{х).
Необходимость:
Пусть функция у = f(х) дифференцируема в точке х. Докажем, что в этой точке существует производная f'(x). Действительно, из дифференцируемости функции у = f(х) в точке х следует, что приращение функции ∆у, отвечающее приращению ∆х аргумента, можно представить в виде
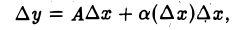
откуда
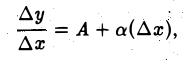
где величина А для данной точки х постоянна (не зависит от ∆х), а а( ∆х) —> 0 при ∆ х —> 0. По теореме о связи функции, имеющей предел, с ее пределом и бесконечно малой функцией, отсюда следует, что
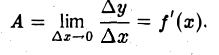
Существование производной доказано. Одновременно мы установили, что А = f'(х).
Достаточность:
Пусть функция f(х) в точке х имеет конечную производную f'(х). Докажем, что f(х) в этой точке дифференцируема. Действительно, существование производной f'(х) означает, что при ∆х0 существует предел отношения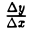 и что
и что
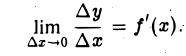
Отсюда, в силу теоремы о связи функции, имеющей предел, с ее пределом и бесконечно малой функцией, вытекает, что
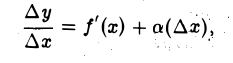
где а( ∆ х) → 0 при ∆ х → 0, и, значит,
∆ у = f'(x) ∆ х + а( ∆ х) ∆ х. (2)
Так как в правой части формулы (2) величина f'(x) не зависит от ∆ х, а а( ∆ х) → 0 при ∆ х → 0, то равенство (2) доказывает, что функция у = f(х) дифференцируема в точке х.
Теорема 1 устанавливает, что для функции f(х) дифференцируемость в данной точке х и существование конечной производной в этой точке — понятия равносильные. Поэтому операцию нахождения производной функции называют также дифференцированием этой функции.
В дальнейшем, когда мы говорим, что функция /(х) имеет производную в данной точке, мы подразумеваем наличие конечной производной, если не оговорено противное.
Непрерывность дифференцируемой функции
Теорема:
Если функция у = f(x) дифференцируема в данной точке х, то она непрерывна в этой точке.
Действительно, если функция у = f(x) дифференцируема в точке х, то приращение Ау этой функции, отвечающее приращению ∆ х аргумента, может быть представлено в виде
∆ у = A∆ х + а( ∆ х) ∆ х, (3)
где А — постоянная для данной точки х, а а( ∆ х) → 0 при ∆ х → 0. Из равенства (3) следует, что
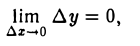
что и означает, согласно определению, непрерывность функции у = f(х) в данной точке х.
Обратное заключение неверно: из непрерывности функции f(х) в некоторой точке х не следует дифференцируемость функции в этой точке.
Пример:
Например, функция f(x) = |х| непрерывна в точке х = 0, но, как мы показали выше (с. 236), не имеет производной в точке х = 0 и потому не является дифференцируемой в этой точке.
Приведем еще пример.
Пример:
Функция
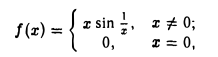
непрерывна на интервале (- ∞ , + ∞ ). Для всех х ≠ 0 она имеет производную, но в точке х = 0 она не имеет ни правой, ни левой производной, потому что величина
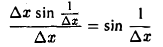
не имеет предела, как при ∆ х → 0 + 0, так и при ∆ х → 0 — 0.
В приведенных примерах производная отсутствует лишь в одной точке. Так и думали в XVIII и начале XIX в., когда считали, что непрерывная функция может не иметь производной самое большее в конечном числе точек. Позже были построены (Больцано, Вейерштрасс, Пеано, Ван дер Варден) примеры непрерывных на отрезке [а, b] функций, не имеющих производной нив одной точке отрезка.
Понятие дифференциала функции
Пусть функция у = f(х) дифференцируема в точке х, т.е. приращение ∆у этой функции, отвечающее приращению ∆y: аргумента, представимо в виде
∆у = A∆ х + а( ∆ х) ∆ х.(4)
где а( ∆ х) → 0 при ∆ х → 0.
Определение:
Если функция у = f(х) дифференцируема в точке х, то часть приращения функции А ∆х при А ≠ 0 называется дифференциалом функции у = f(х) и обозначается символом dy или df(x):
dy = A ∆х. (5)
В случае А ≠ 0 дифференциал функции называют главной линейной частью приращения ∆у функции, поскольку при ∆х → 0 величина а( ∆х) ∆х в равенстве (4) есть бесконечно малая функция более высокого порядка, чем А ∆х.
В случае, когда А = 0, считают, что дифференциал dy равен нулю.
В силу теоремы 1 имеем А = f'(х), так что формула (5) для dy принимает вид
dy = f'(x) ∆х. (6)
Наряду с понятием дифференциала функции вводят понятие дифференциала dx независимой переменной х, полагая по определению
dx = ∆х.
Тогда формулу для дифференциала функции у = f(x) можно записать в более симметричной форме
dy = f'(x) dx.
Отсюда в свою очередь имеем: f'(х) = Это еще одно обозначение производной (обозначение Лейбница), которую можно рассматривать как дробь — отношение дифференциала функции dy к дифференциалу аргумента dx.
Введем еше одно понятие. Будем говорить, что функция у = f(х) дифференцируема на интервале (а, b), если она дифференцируема в каждой точке этого интервала.
Геометрический смысл дифференциала
Пусть имеем кривую, заданную уравнением у = f(х),где f(х) — дифференцируемая в точке х ∈ (а,b). Проведем касательную к этой кривой в точке М (х, у) и отметим на кривой еще точку М1 с абсциссой х + dx. Как известно, f'(x) есть угловой коэффициент касательной, т. е. f'(х) = tg φ.
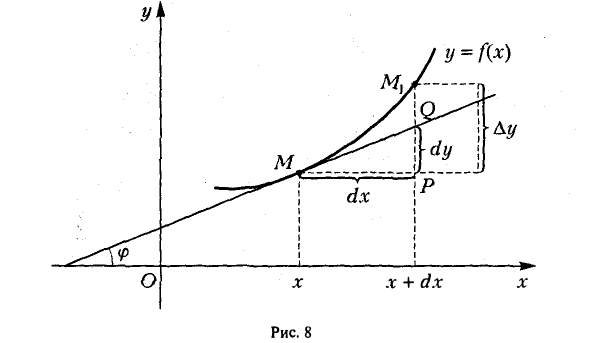
Рассмотрим треугольник MPQ (рис. 8). Из рисунка видно, что
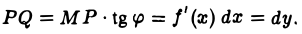
Таким образом, дифференциал dy = f ‘(x)dx функции у = f(х) есть приращение ординаты касательной, проведенной к кривой у = f(x) в точке с абсциссой х, при переходе отточки касания к точке с абсциссой х + dx.
Дифференцирование суммы, произведения и частного
Если функции и(х) и v(x) имеют производную в точке х, то в этой точке имеют производную их сумма и(х) + v(x), разность и(х) — v(x), произведение и(х) ⋅ v(x) и частное 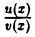 (последнее при дополнительном условии v(x) ≠ 0), причем
(последнее при дополнительном условии v(x) ≠ 0), причем
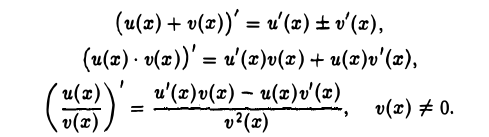
Докажем, например, правило дифференцирования частного, Из дифференцируемости функции v(x) в точке х следует непрерывность v(x) в этой точке, а из условия v(x) ≠ 0 в силу устойчивости знака непрерывной функции вытекает, что v (х+ ∆х) ≠ 0 для всех достаточно малых | ∆х|. Поэтому отношение
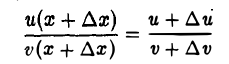
определено для всех ∆х, достаточно малых по абсолютной величине.
Дадим х прирашение ∆х. Тогда функция у = 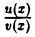 получит приращение
получит приращение
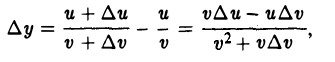
откуда
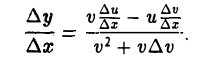
По условию существуют
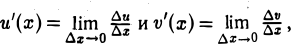
так что ∆v → 0 при ∆x → 0.
Что касается величин и и v, то они для данной точки х являются постоянными, причем v(x) ≠ 0. Таким образом, правая часть равенства (1) имеет предел при ∆ х → 0, равный 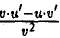 . Следовательно, существует и предел левой части (1), т. е. существует
. Следовательно, существует и предел левой части (1), т. е. существует
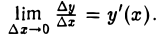
Переходя в равенстве (1) к пределу при ∆ х → 0, получаем
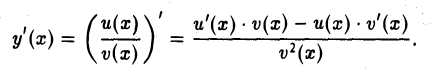
Пример:
Найти производную функции 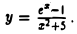
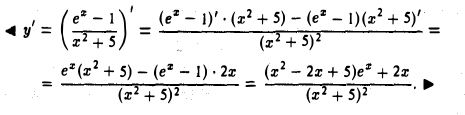
Следствие:
Постоянный множитель можно выносить за знак производной
{Си(х))’ = Си'(х).
Следствие:
Если функции u1(x), u2(x), …, ип(х) (п — конечное) имеют производную в точке х, то в этой точке имеют производную их сумма и произведение, причем
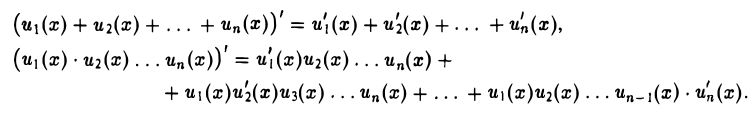
Задача:
Что можно сказать о дифференцируемое суммы f(x) + φ(x) в точке х, если в этой точке функция f(x) дифференцируема, а функция φ(х) не дифференцируема?
Задача:
Пусть функция f(х) дифференцируема в точке хо и f(xо) ≠ 0. а функция φ(х) не дифференцируема в этой точке. Доказать, что произведение f{x) • φ(х) является недифференцируемым в точке xo.
Задача:
Пусть функции f(г) и φ(х) не имеют производной в точке xo. Следует ли отсюда, что в этой точке не имеют производной функции
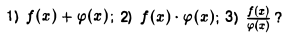
Рассмотреть примеры.
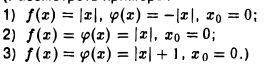
Отсюда
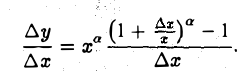
Учитывая, что
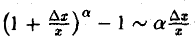
при ∆х → 0, получим
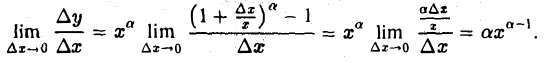
Итак,
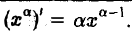
Производные тригонометрических функций
Рассмотрим функцию у = sin х, — ∞ < х < + ∞. Во всякой точке х и для любого ∆х
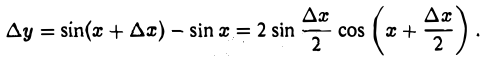
Отсюда
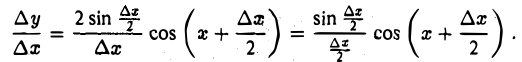
Учитывая, что
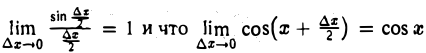
в силу непрерывности функции у = cos х во всякой точке х, получаем
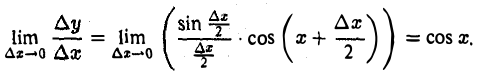
Итак
(sin х)’ = cos х. (1)
Аналогично получаем
(cos х)’ = — sin x. (2)
Пользуясь формулами (1) и (2) и правилом дифференцирования частного, найдем производную от функции у = tg х:
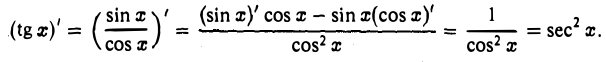
Итак,
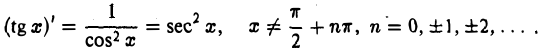
Аналогично находим
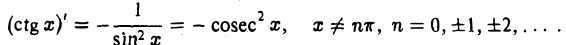
Дифференцирование сложной функции
Теорема:
О дифференцировании сложной функции. Если функция и = φ(х) дифференцируема в точке х0> а функция у = f(u) дифференцируема в соответствующей точке uo = φ(xо), то сложная функция у = f[φ(х)] дифференцируема в точке хо, причем
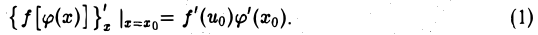
Дадим значению х = х0 приращение ∆х. Тогда функция и = φ(x) получит приращение ∆и, а это в свою очередь при ∆и Ф 0 вызовет приращение ∆у функции у = f(u). По условию функция у = f(и) дифференцируема в точке uo, поэтому приращение ∆у этой функции может быть представлено в виде
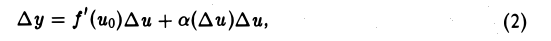
где а( ∆и) 0 при ∆и → 0.
Функция а( ∆u) вообще не определена при ∆и = 0. Доопределим ее, положив а(0) = 0. Тогда а(∆и) будет непрерывной при ∆и = 0. Разделив обе части равенства (2) на ∆х ≠ 0, получим
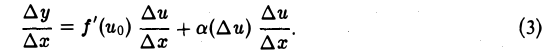
По условию функция и = φ(x) дифференцируема в точке хо и, значит, непрерывна в этой точке. Поэтому при ∆х → 0 приращение ∆и → 0, что вызывает стремление к нулю а( ∆и). Кроме Того, из этого условия следует, что 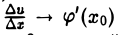 при ∆х0.
при ∆х0.
Следовательно, правая часть (3) имеет предел при ∆х → 0, равный f'(ио)φ'(хо). Поэтому существует и предел левой части равенства (3) при ∆х → 0, т.е. существует 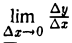 , который есть производная по х сложной функции у = f[у>(х)] в точке хо-Переходя в равенстве (3) к пределу при ∆х → 0, получим
, который есть производная по х сложной функции у = f[у>(х)] в точке хо-Переходя в равенстве (3) к пределу при ∆х → 0, получим
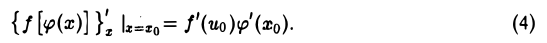
Здесь символ f'(uo) означает производную функции f(и) по ее аргументу и (а не х), вычисленную при значении и0 = о) этого аргумента.
Равенство (4) можно записать в виде
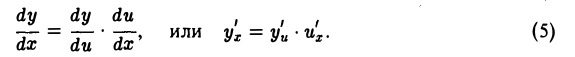
Пример:
Найти производную функции 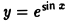
Здесь у есть сложная функция аргумента х: у = 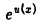 , где u(x) = sin x. Поэтому
, где u(x) = sin x. Поэтому
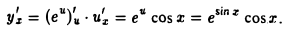
Пример:
Найти производную функции
y = ln|x|, х ≠ 0.
Эта функция определена на всей числовой оси, исключая точку х = 0; четная. Если х > 0, то |z| = х и In |х| = In х, так что
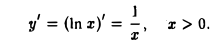
Если х < 0, то |х| = -х и In \х\ = ln(-x).
Представим функцию у = lп(-x) как сложную функцию, положив
у = In u, и = -x.
По правилу дифференцирования сложной функции
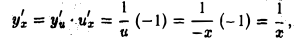
так что и для х < 0
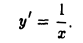
Таким образом,
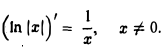
Замечание. Теорема может быть обобщена на случай любой конечной цепочки функции. Так, если
у = f(и), и = φ(t), z = ψ(x), так что у =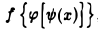 причем существуют производные
причем существуют производные 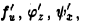 то
то
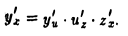
Инвариантность формы дифференциала
Если у = f(u) — дифференцируемая функция независимой переменной и, то
dy = f'(u) du, (6)
где дифференциал независимой переменной равен ее произвольному приращению:
du = ∆и.
Пусть теперь аргумент и дифференцируемой функции у = f(u) сам является дифференцируемой функцией и = φ(х) независимой переменной х. В таком случае у можно рассматривать как сложную функцию у = f[φ(x)] аргумента х. Поскольку аргумент х является независимой переменной, то для сложной функции у = f[φ(x)] дифференциал dy представляется в виде

По правилу дифференцирования сложной функции
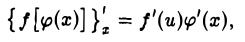
поэтому формула (7) примет вид
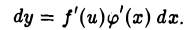
Замечая, что φ'(х) dx = du, получим для dy выражение
dy = f'(и) du.
совпадающее с (6).
Таким образом, дифференциал функции выражается формулой одного и того же вида как в случае функции от независимой переменной, так и в случае функции от функции. Это свойство дифференциала называют инвариантностью формы дифференциала.
Следует обратить внимание на то, что если и — независимая переменная, то в формуле дифференциала dy = f'(u) du величина du равна ∆и — произвольному приращению независимой переменной; когда же и = φ(х), то du = φ'(x) dx есть линейная часть приращения функции и = φ(х), в общем случае не равная ∆и.
Понятие обратной функции. Производная обратной функции
Пусть функция у = f(x) задана на отрезке [а, b] и пусть множеством значений этой функции является отрезок [а, β] оси Оу. Пусть, далее, каждому у из [а, β] соответствует только одно значение х ∈ [а, b], для которого f(х) = у (рис. 9). Тогда на отрезке [а, β] можно определить функцию х = φ{у), ставя в соответствие каждому у € (а, β] то значение х € [а, b], для которого f(x) = у. Функция х = φ(у) называется обратной для функции у = f(x).
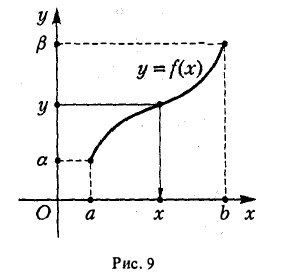
Если х = φ(у) — обратная функция для у = f{х), то, очевидно, функция у = f(x) является обратной для функции х = φ(у). Поэтому функции у = f(x) и x = у>(у) называют взаимно обратными. Для взаимно обратных функций имеют место соотношения
(1)
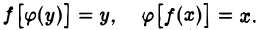
Укажем еше один, более конструктивный, подход к понятию обратной функции. Если уравнение у = f(x), определяющее у как функцию от х, можно разрешить относительно х так, что каждому значению у соответствует одно определенное значение х, то получим уравнение х = φ(у), определяющее х как функцию у. Эта функция х = φ(у) является обратной по отношению к функции у = f(x).
Примеры:
- у = 3x на (0, 1]; обратная функция х =
 на [0, 3].
на [0, 3]. - у = x3, -cc< х < + ∞; обратная функция х =
 — ∞ < у < + ∞ .
— ∞ < у < + ∞ .
3.

Очевидно, уравнения у = f(х) и х = φ(y) определяют одну и ту же кривую на плоскости хОу.
Если в обоих случаях откладывать значения аргументов на оси абсцисс, а значения функции на оси ординат, т. е. вместо уравнений у — f(x) и х = φ(у) рассматривать уравнения у = f(х) и у = φ(х), то график функции у = φ(х) будет симметричен графику функции у = f(х) относительно биссектрисы 1-го и 3-го координатных углов (рис. 10).
Определение:
Функция у — f(x) называется возрастающей на некотором отрезке [а, b], если для любых х1 и х2 из отрезка [а, bJ, удовлетворяющих условию х1 < x2, справедливо неравенство f(x1) < f(x2).
Пример:
Такова, например, функция f(x) = x3 на любом отрезке [а, b].
Теорема:
Если функция у = f(х) непрерывна и возрастает на отрезке [а, b], причем f(а) = a, f(b) = р, то она имеет обратную функцию х = φ(у), которая определена, непрерывна и возрастает на отрезке [a, /3].
Ограничимся геометрическим пояснением теоремы (рис. 11). Кривая АВ является графиком функции у = f(х), непрерывной и возрастающей на [а, b]. Из рисунка видно, что каждому значению у ∈ [а, b] отвечает одно значение х ∈ [а, b], для которого f(х) = у. Поэтому той же кривой АВ величина х выражается как функция у на [а, β ]: х = φ(у). Это и есть функция, обратная к у = f(х). Она на отрезке [а, β ] непрерывна (ее графиком является та же непрерывная кривая АВ) и возрастает, т. к. большему значению аргумента у отвечает большее значение функции х = φ(у).
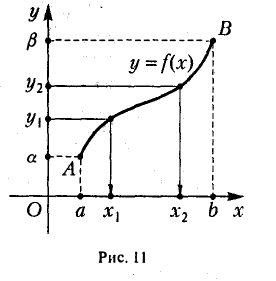
Аналогичное утверждение справедливо и для непрерывной убывающей на [а, b] функции.
Производная обратной функции
Теорема:
Пусть функция у = f(х) непрерывна и возрастает (убывает) в некоторой окрестности точки х0 и пусть в точке Хо существует производная f'(хо) ≠ 0. Тогда обратная функция х = φ(у) имеет производную в точке уо = f(х0), причем

Рассмотрим функцию х = φ{у). Дадим значению у = уо приращение ∆у. Тогда функция х = φ(у) получит некоторое приращение ∆х
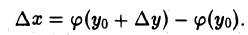
При этом в силу возрастания (убывания) обратной функции при ∆у ≠ 0 обязательно ∆х ≠ 0. Поэтому отношение 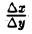 можно представить в виде
можно представить в виде
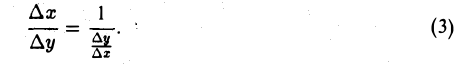
Если теперь ∆у устремить к нулю, то и ∆х будет стремиться к нулю, т. к. обратная функция х = φ (у) также непрерывна в точке уо.
По условию функция у = f(х) имеет в точке хо производную f'(хо) ≠ 0. Следовательно, при ∆ у —> 0 (когда и ∆ х —» 0), предел частного 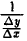 существует и равен
существует и равен 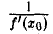 ,
,
Из равенства (3) вытекает поэтому, что при ∆у → 0 существует предел отношения 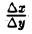 , причем
, причем
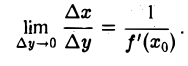
Но предел отношения 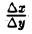 при ∆ у → 0 есть производная φ'(у0) функции х = φ(y) в точке у = уо. Таким образом, (4)
при ∆ у → 0 есть производная φ'(у0) функции х = φ(y) в точке у = уо. Таким образом, (4)
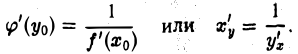
или
Геометрически результат теоремы достаточно прозрачен. Существование производной функции у = f(x) в точке хо эквивалентно существованию касательной к графику этой функции в точке М0(хо, f(xо)). Поэтому, если существует касательная к кривой у = f(x) в точке М0(х0, уо), не параллельная оси Ох, то она будет касательной и к графику функции х = φ(у) (та же кривая!) в точке Mо (рис. 12). При этом f'(xо) = tg а, φ'(yо) = tg β и, поскольку
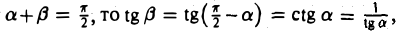
т. е.
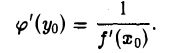
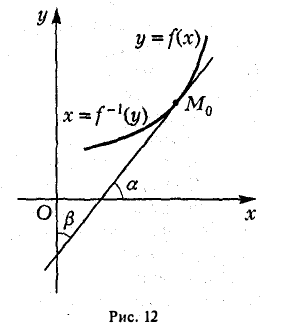
Формулу (4) записывают также в виде (5)
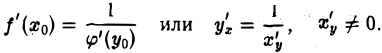
Формулы (4) и (5) можно получить совсем просто. Пусть у = f(x) и х = φ (у) — взаимно обратные дифференцируемые функции. Тогда
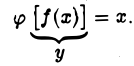
Дифференцируя обе части по х и пользуясь правилом дифференцирования сложной функции, получим
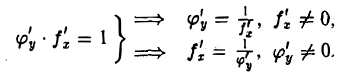
Производные обратных тригонометрических функций
- Функция у = arcsin х определена на отрезке [-1, 1] (рис. 13) и является обратной для функции х = sin у на отрезке —
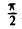 ≤ у ≤
≤ у ≤ 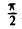 Рассмотрим интервал -1 < х < 1. Функциях = sin у имеет для соответствующих значений у ∈ (—
Рассмотрим интервал -1 < х < 1. Функциях = sin у имеет для соответствующих значений у ∈ (—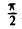 ,
,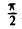 ) положительную производную х’у = cos у. В таком случае существует также производная у’х, равная, согласно (5),
) положительную производную х’у = cos у. В таком случае существует также производная у’х, равная, согласно (5), 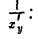
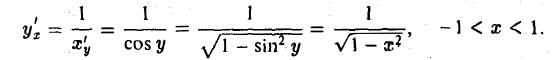
Корень 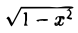 берем со знаком «+», т. к. cos у > 0 для у ∈ (-
берем со знаком «+», т. к. cos у > 0 для у ∈ (-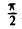 ,
,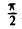 ). Итак,
). Итак,
(6)
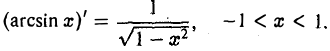
Мы исключаем значения х = ±1, поскольку для соответствующих значений у = ±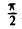 производная х’у = cos у равна нулю и правая часть (6) теряет числовой смысл.
производная х’у = cos у равна нулю и правая часть (6) теряет числовой смысл.
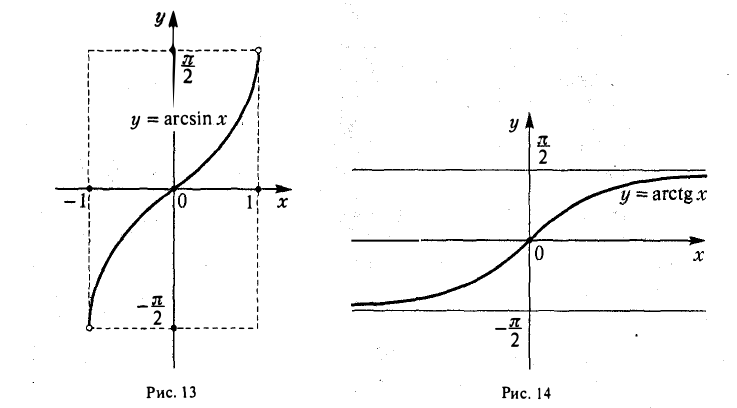
2. Функция у = arctg х, — ∞ < х < + ∞ (рис. 14) служит обратной для функции x = tg y, ~ 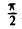 < y <
< y < 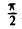 по формуле (5)
по формуле (5)
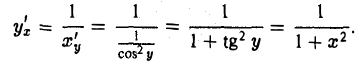
Итак
(7)
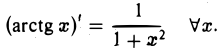
Чтобы найти формулы для производных arccos х и arcctg х, достаточно заметить, что
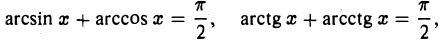
откуда
(8)
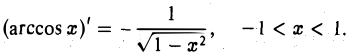
(9)
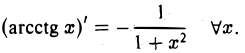
Производные гиперболических функций
По определению гиперболический синус sh х = 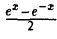 , гиперболический косинус ch х =
, гиперболический косинус ch х =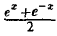 .
.
Отсюда легко находим
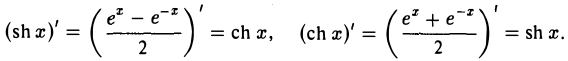
По определению гиперболический тангенс 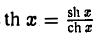 гиперболический котангенс cth х =
гиперболический котангенс cth х = 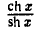
Пользуясь правилом дифференцирования частного и тождеством
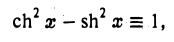
получаем
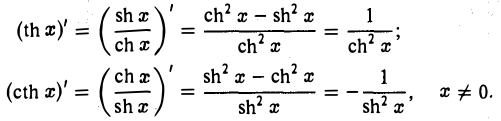
Таблица производных основных элементарных функций

Логарифмическое дифференцирование
При отыскании производной сложной функции иногда бывает удобным следующий прием, называемой логарифмическим дифференцированием. Пусть требуется найти производную функции у = f(х) > 0 и пусть функция tp(x) = ln f(x) дифференцируется значительно проще. Тогда поступаем так. Беря натуральный логарифм данной функции, будем иметь
ln у = ln f(x),
или
ln у = φ(х). (1)
Дифференцируя обе части (1) по х и учитывая, что у есть функция от х, найдем
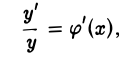
откуда у1 = у • φ(х), или (2)
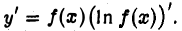
Логарифмическое дифференцирование особенно удобно при дифференцировании сложной степенно-показательной функции, т.е. функции вида
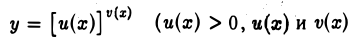
— дифференцируемые функции).
Имеем
ln у = v(x) ln и(х).
Дифференцируя обе части последнего равенства, получаем
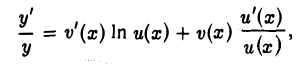
откуда
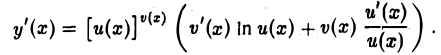
Пример:
Найти производную функции

Беря натуральные логарифмы от обеих частей равенства (*), получаем
In у = х In х,
откуда
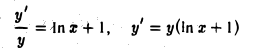
или
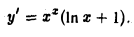
Применение дифференциалов в приближенных вычислениях
Пусть функция у = f(х) дифференцируема в точке х0, так что приращение функции ∆у, отвечающее приращению ∆х аргумента, представимо в виде
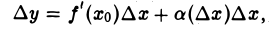
где f'(хо) ∆х = dy(x0), а( ∆х) → 0 при ∆х 0. Если dу(х0) ≠ 0 и, значит, f'(х0) ≠ 0, то
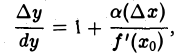
так что при ∆х → 0 бесконечно малые ∆у и dy эквивалентны и их разность ∆у — dy есть бесконечно малая более высокого порядка, чем они сами. Поэтому мы можем брать величину dy в качестве приближенного значения ∆у:
∆у ≈ dy.
Таким образом, если dy(xo) ≠ 0,то для приближенного вычисления значения функции в точке х0 + ∆х можно пользоваться формулой
f(х0 + ∆х) ≈ f(х0) +f'(хо) ∆х, (1)
причем абсолютная и относительная погрешности будут как угодно малы при достаточно малом | ∆х|.
Пусть, например, у = хβ, β ∈ R. Тогда
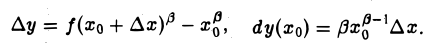
При малых значениях | ∆х| полагаем
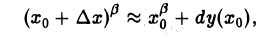
или
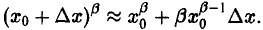
В частности, при β = 1/2
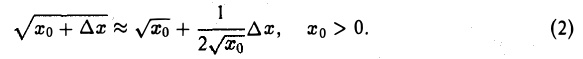
Пример:
Вычислить приближенно 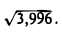
Полагаем x0 = 4, ∆x = -0,004, получим по формуле (2)
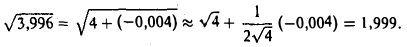
Производные высших порядков
Если функция f(х) имеет производную f'(х) в каждой точке х интервала (а, b ), то f'(х) есть функция от х, определенная на интервале (а, b). Может оказаться, что и f'(x) в точке х ∈ (а, b) в свою очередь имеет производную, которую называют производной 2-го порядка функции f(х) (или второй производной) и обозначают символом f»(х) или f(2)(х). Таким образом
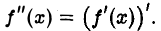
Производные более высоких порядков определяются аналогично. Именно, производная п-го порядка функции f(х) есть производная от производной (п — 1)-го порядка этой функции:
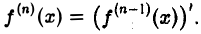
Число п, указывающее порядок производной, заключают в скобки, чтобы не путать с показателем степени.
Чтобы найти f(п)(x)> надо сначала найти f'(x), затем f»(х), взяв производную от f'(х), и т. д., пока не получим производную нужного порядка. Таким образом, производные высших порядков вычисляются при помощи уже известных правил и формул дифференцирования. . .
Примеры:
- Вычислим п-ю производную функции у = ekx, k = const. Последовательно дифференцируя, будем иметь
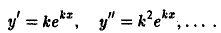
По методу математической индукции получаем
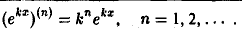
2. Вычислим n-ю производную функции у = sin х. Имеем
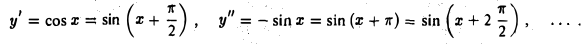
Методом индукции устанавливаем
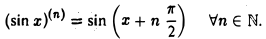
3. Аналогично получаем формулу
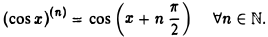
Множество всех функций f(x), определенных на интервале (а, b) и имеющих в каждой точке х ∈ (а, b) непрерывную производную п-го порядка, обозначается Сn(а, b). Функцию f(х), имеющую производную любого порядка в каждой точке х ∈ (а, b), называют бесконечно дифференцируемой на (а, b) и пишут f(x) ∈ С∞ (а, b). Так, функции ez, sin х, cosx бесконечно дифференцируемы на (- ∞, + ∞).
Замечание:
Производные четвертого порядка и выше иногда обозначают римскими цифрами и без скобок, т. е. пишут
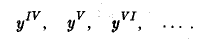
Механический смысл второй производной
Пусть S = S(t) — закон прямолинейного движения материальной точки. Тогда, как известно, S'(t) = v(t) — мгновенная скорость движущейся точки в момент времени t. В таком случае вторая производная S»(t) равна v'(t),т.е. ускорению a(t) движущейся точки в момент времени t:
S»(t) = a(t).
Производные высших порядков суммы и произведения функций
Если функции и(х) и v(x) имеют производные п-го порядка в точке х, то функции и(х) ± v(x) и и(х) • v(x) также имеют производные п-го порядка в этой точке, причем
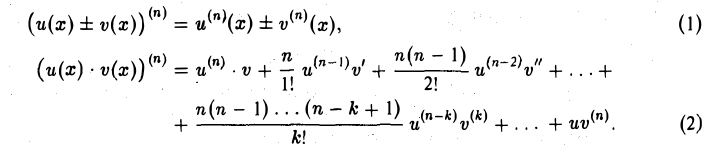
Формулы (1) и (2) доказываются по индукции. Для формулы (1) это делается без труда (проделайте самостоятельно). Остановимся несколько подробнее на выводе формулы (2). Если у = и(х) • v(x),to
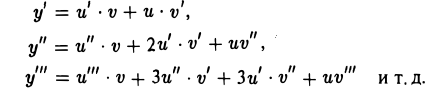
Легко подметить закон, по которому построены все эти формулы: правые части их напоминают разложение степеней бинома (и + v)1, (и + v)2, (и + v)3, лишь вместо степеней и и v стоят порядки производных. Сходство становится еще более полным, если в полученных формулах вместо u, v писать и(0), v (0) (производные нулевого порядка). Формула (2) носит название формулы Лейбница.
Пример:
Пользуясь формулой Лейбница, найти y(1001) 0т функции у = х2еx.
Имеем
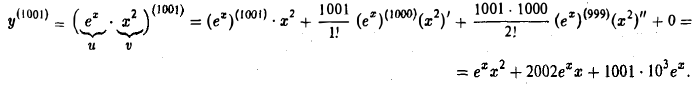
Отметим еще полезную формулу. Пусть х = φ(у) и у = f(x)~ взаимно обратные функции и пусть f'(x) ≠ 0. Тогда
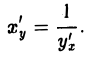
Далее,
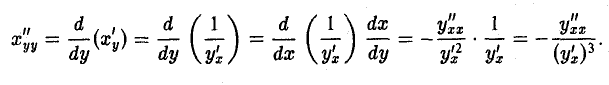
Дифференциалы высших порядков
Пусть функция у = f(x) дифференцируема в точке х. Может оказаться, что в точке х дифференциал dy = f'(x)dx, рассматриваемый как функция х, есть также дифференцируемая функция. Тогда существует дифференциал от дифференциала данной функции, который называется дифференциалом второго порядка функции у = f(x) и обозначается d2y. Таким образом,
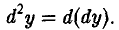
Аналогично определяются дифференциалы более высоких порядков: дифференциалом п-го порядка dny функции у = f(x) называется дифференциал от дифференциала (п — 1)-го порядка этой функции
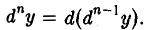
Дифференциал dy естественно называть дифференциалом 1 -го порядка от функции
y = f(x).
Найдем формулы, выражающие дифференциалы высших порядков. Пусть у = f(х) есть функция независимой переменной х, имеющая дифференциалы любого порядка. Тогда
dy = f'(x) dx,
где dx = ∆х есть некоторое приращение независимой переменной х, которое не зависит от х. По определению
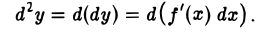
Т.к. здесь f'(x)dx рассматривается как функция от х, то множитель dx является постоянным и его можно вынести за знак дифференциала. Поэтому
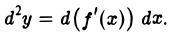
Для вычисления d(f'(x)) применим формулу дифференциала первого порядка к функции f'(x). Получим
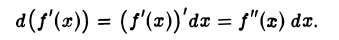
Следовательно, дифференциал d2y второго порядка функции у = f(x) в точке х, соответствующий тому же дифференциалу dx независимой переменной х, определится формулой
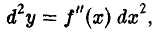
где dx2 обозначает (dx)2.
Пользуясь методом математической индукции, получаем формулу дифференциала n-го порядка
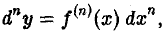
где dxn = (dx)n. Отсюда
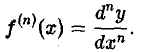
Пусть теперь у = f(и), где и = φ(х) — функция, дифференцируемая достаточное число раз. Тогда в силу инвариантности формы первого дифференциала
dy = f'(u) du.
Здесь du = φ'{x) dx в общем случае не является постоянной величиной, поэтому
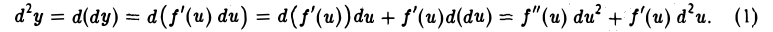
В случае, когда и — независимая переменная, d2u = 0 и

Сравнивая формулы (1) и (2), заключаем, что уже второй дифференциал инвариантностью формы не обладает.
Заметим, что если u = φ(х) есть линейная функция х, т. е. и = ax+b (a, b = const), инвариантность формы сохраняется.
Дифференцирование функции, заданной параметрически
Введем на плоскости декартову прямоугольную систему координат хОу. Пусть функции ψ(t) и φ(t) непрерывны на отрезке а ≤ t ≤ β изменения параметра. Если параметр t рассматривать как время, то указанные функции определяют закон движения точки М с координатами
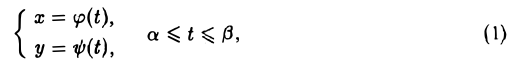
на плоскости хОу.
Определение:
Множество {М} всех точек плоскости, координаты (х, у) которых определяются уравнениями (1),называют плоской кривой. Говорят в этом случае, что кривая задана в параметрической форме.
Пример:
Так, например, окружность радиуса R с центром в начале координат можно задать в параметрической форме уравнениями
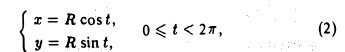
где t — радианная величина угла между осью Ох и радиус-вектором ОМ , проведенным в точку М (х, у) (рис. 15).
Если из системы уравнений (1) исключить параметр t, то останется одно уравнение, содержащее х и у, и тогда данная кривая будет определяться уравнением F(x, у) = 0. Так, если в уравнениях (2) возведем в квадрат левые и правые части и затем полученные уравнения почленно сложим, то параметр t будет исключен и данная окружность будет выражаться уже знакомым нам уравнением х2 + у2 = R2. Однако исключить параметр t не всегда бывает возможно. И тем не менее, для решения некоторых задач, как, например, для отыскания касательной к кривой, надо уметь находить производную от у по х и в таких случаях, когда кривая задана в параметрической форме.
Будем говорить, что функциональная зависимость у от х задана параметрически, если обе переменные х и у заданы как функции параметра t :
Рассмотрим вопрос о вычислении производной от у по х в случае параметрического задания функции.
Пусть функции х = φ(t) и у = ψ(t) определены и непрерывны на некотором интервале (а, β) изменения t. Пусть для функции х = φ'(t) существует обратная функция t = g(х). Тогда у есть сложная функция от х:

Допустим, что функции φ(t) и ψ(t) дифференцируемы в точке t е (а, β), причем φ'(t) ≠ 0, а функция t = g(х) дифференцируема в соответствующей точке х. Тогда, согласно правилу дифференцирования сложной функции, будет дифференцируемой в точке х и функция  причем
причем
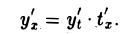
Но по правилу дифференцирования обратной функции
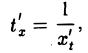
так что
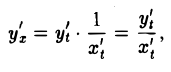
или
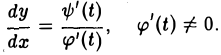
Формально этот результат получается мгновенно: производную 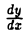 рассматриваем как дробь и делим числитель и знаменатель на dt, что дает
рассматриваем как дробь и делим числитель и знаменатель на dt, что дает
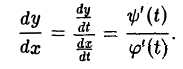
Для окружности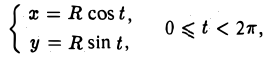
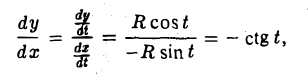
или 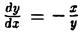 (пояснить результат геометрически).
(пояснить результат геометрически).
Если функции φ(t) и ψ{t) имеют производные k-ro порядка, причем φ'(t) ≠ 0, то и функция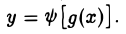 ] имеет производную k-ro порядка по х. Производная 2-го порядка от у по х вычисляется так:
] имеет производную k-ro порядка по х. Производная 2-го порядка от у по х вычисляется так:
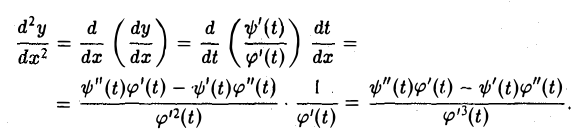
Таким образом,
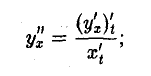
вообще
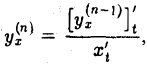
где у = f(х) — функция, заданная параметрическими уравнениями х = x(t), у = y(t).
Пример:
Найти 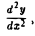 , если
, если
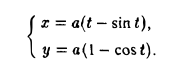
Имеем
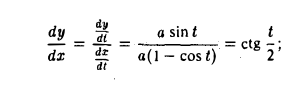
далее
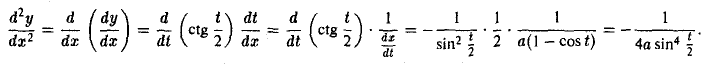
Вектор-функция скалярного аргумента
Пусть материальная точка М движется по некоторой траектории L. Тогда каждому значению времени t соответствует определенная длина и направление радиус-вектора г этой точки, а также ее скорости v, ускорения w и т. д.
Следовательно, каждый из этих векторов можно рассматривать как некоторую векторную функцию скалярного аргумента t:
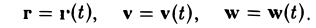
Определение:
Если каждому значению скалярного аргумента t из интервала (а, β) соответствует по некоторому закону определенный вектор а, то говорят, что на интервале (а, β) задана вектор-функция скалярного аргумента t и пишут
a = a(t). (1)
Пусть вектор а разложен по координатным ортам i, j, к некоторой фиксированной системы координат
n = xi + yj + zk. (2)
Если а = п(t) есть какая-либо векторная функция аргумента t, то ее координаты x,y,z будут также некоторыми (скалярными) функциями этого аргумента:
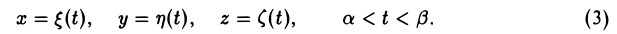
Обратно, если координаты х, у, z вектора а являются функциями аргумента t, то функцией аргумента t будет и сам вектор а:

Таким образом, задание одной вектор-функции а = a(t) равносильно заданию трех скалярных функций (3) и обратно.
При изменении аргумента t вектор а(t), вообще говоря, меняет длину и направление (а в некоторых случаях и точку приложения, как, например, вектор скорости).
Определение:
Годографом вектор-функции a(t) называется множество точек, которое прочерчивает конец вектора a(t) при изменении аргумента t, когда начало вектора а(<) помещено в фиксированную точку О пространства.
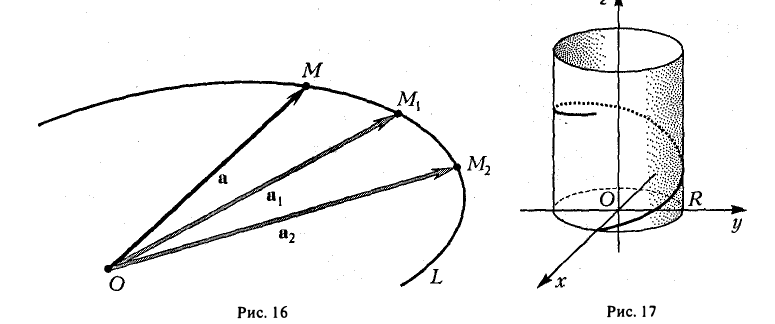
Годограф а(t) есть вообще некоторая кривая L в пространстве (рис. 16). Годографом радиуса-вектора г движущейся точки будет сама траектория L этой точки. Уравнение
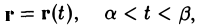
или
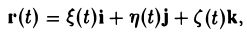
называется векторным уравнением кривой L. Уравнения
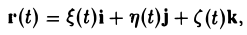
называются параметрическими уравнениями этой кривой. Пример. Например, уравнения
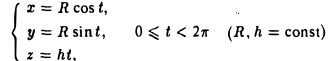
являются параметрическими уравнениями одного витка винтовой линии (рис. 17).
Пусть вектор-функция а = а(t) определена в некоторой окрестности точки t = t0 кроме, быть может, самой этой точки.
Определение:
Постоянный вектор А называется пределом вектор-функции а(t) при t → t0, если для всякого δ > 0 существует δ > 0 такое, что для всех t ≠ t0, удовлетворяющих условию |t — t0| < δ. верно неравенство
|a(t) — А| < ε.
В этом случае пишут
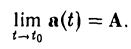
Геометрически это означает, что при t → tо длина вектора а(t) — А стремится к нулю, т.е. что вектор а(t) при t → t0 приближается по своей длине и направлению к вектору А (рис. 18).
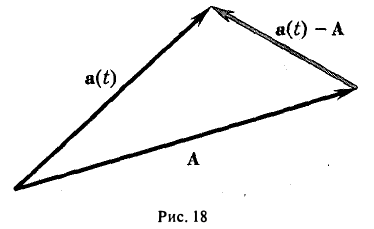
Таким образом,
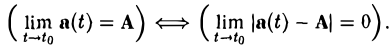
Пусть
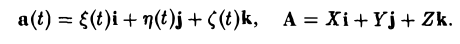
Тогда
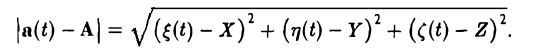
Отсюда, если 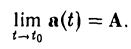 , то
, то
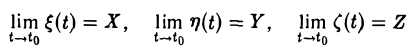
и наоборот.
Пусть вектор-функция а = a(t) определена на интервале а < t < β и to ∈ (а, β).
Определение:
Вектор-функция а(t) называется непрерывной при t = to, если
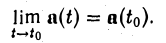
Производная вектор-функции по ее скалярному аргументу
Пусть вектор-функция п = а(t) определена на интервале а < t < β и пусть кривая L есть годограф a(t). Возьмем какое-нибудь фиксированное значение аргумента t ∈ (а, β). Ему отвечает точка М кривой L. Дадим t любое приращение ∆t, но такое, что t + ∆t ∈ (а, β). Тогда получим вектор a(t + ∆t), который определит на кривой L некоторую точку М1 (рис. 19).
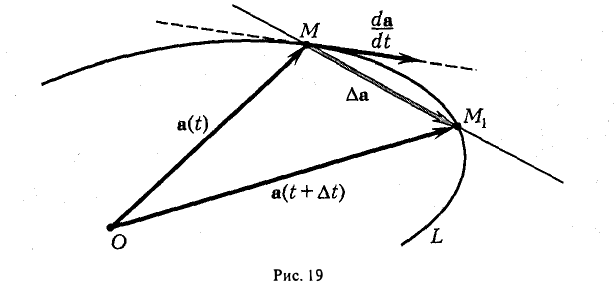
Рассмотрим приращение ∆а вектор-функции a(t), отвечающее приращению ∆t аргумента:
∆а = a(t + ∆t) — a(t).
Составим отношение
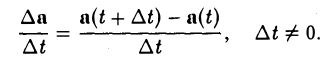
Это новый вектор, коллинеарный вектору ∆а.
Определение:
Если при ∆t —► 0 разностное отношение 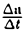 имеет предел, то этот предел называется производной вектор-функции a(t) по ее аргументу t в данной точке t и обозначается
имеет предел, то этот предел называется производной вектор-функции a(t) по ее аргументу t в данной точке t и обозначается 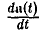 или a'(t).
или a'(t).
Таким образом,
(1)
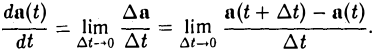
В этом случае a(t) называется дифференцируемой в точке t.
Выясним направление вектора 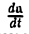 . При ∆t —> 0 точка М1 стремится по годографу к точке М, и потому секущая MMt стремится к касательной к кривой L в точке М. Следовательно, производная
. При ∆t —> 0 точка М1 стремится по годографу к точке М, и потому секущая MMt стремится к касательной к кривой L в точке М. Следовательно, производная 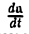 представляет собой вектор, касательный к годографу функции a(t) в точке М. Направлен же вектор
представляет собой вектор, касательный к годографу функции a(t) в точке М. Направлен же вектор 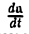 в ту сторону, куда перемешается конец вектора a(t) по годографу при возрастании параметра t (рис. 19).
в ту сторону, куда перемешается конец вектора a(t) по годографу при возрастании параметра t (рис. 19).
Найдем выражение для производной 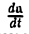 в координатах. Пусть
в координатах. Пусть
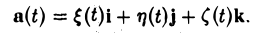
Тогда
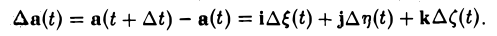
Деля обе части ∆t ≠ 0, получим
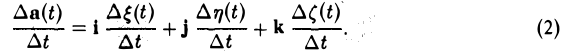
Если функции ξ(t), η(t), ζ(t) имеют производную при выбранном значении t, то при ∆ → 0 каждое слагаемое в правой части равенства (2) имеет предел, так что существует и предел левой части, т.е. существует 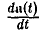 . Переходя в равенстве (2)
. Переходя в равенстве (2)
к пределу при ∆t → 0, получаем
(3)
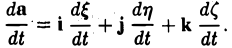
Итак, если вектор a(t) отнесен к неподвижной системе координат, то его производная 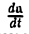 выражается формулой (3).
выражается формулой (3).
Таким образом, вычисление производной вектор-функции а(t) сводится к вычислению производных ее координат.
Если r = r(t) есть радиус-вектор движущейся в пространстве точки, то 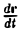 — скорость этой точки в момент времени t:
— скорость этой точки в момент времени t:
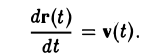
Пример:
Найти производную вектор-функции
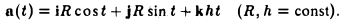
По формуле (3)
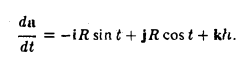
Правила дифференцирования
- Если e — постоянный вектор, то
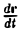 = 0.
= 0.
2. Если векторы а(t) и b(t) имеют производную в точке t, то
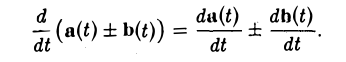
3. Постоянный числовой множитель можно выносить за знак производной
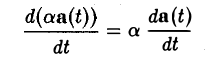
— (а — числовая постоянная).
4. Производная от скалярного произведения векторов выражается формулой
Следствие:
Если вектор e(t) единичный, т. е.
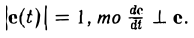
В самом деле, если e — единичный вектор, то
(e, e) = 1.
Беря производную по t от обеих частей последнего равенства, получим
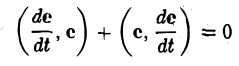
или
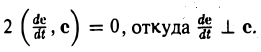
5. Производная векторного произведения векторов определяется формулой
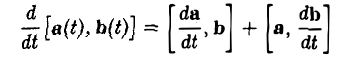
(порядок сомножителей существен).
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

