Оглавление:
Квадратный корень — это такое число, квадрат которого (результат умножения на себя) равен , то есть решение уравнения относительно переменной . Часто под этим понятием подразумевают более узкое — т. н. арифметический квадратный корень — неотрицательное число.
Кубический корень — это число x, куб которого равен a. Другими словами, это решение уравнения x3=a (обычно подразумеваются вещественные решения).
Корни (арифметические)
Определения:
Число, квадрат которого равен а, называется квадратным корнем из числа 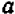 и обозначается
и обозначается 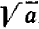 . Так, например,
. Так, например,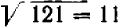 ; в самом деле,
; в самом деле, 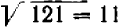 .
.
Число, куб которого равен 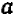 , называется кубическим корнем из числа
, называется кубическим корнем из числа 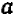 и обозначается
и обозначается 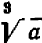 . Так, например,
. Так, например, 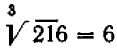 , так как
, так как 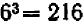 .
.
Вообще число, 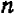 -я степень которого равна
-я степень которого равна 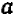 , называется корнем степени
, называется корнем степени 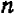 из числа
из числа 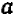 и обозначает
и обозначает 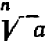 . Например,
. Например, 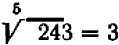 , так как
, так как 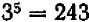 . Если
. Если 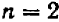 , то показатель при корне писать не принято.
, то показатель при корне писать не принято.
Нахождение корня некоторой степени из данного числа называется извлечением корня. Конечно, не из всякого числа можно извлечь корень данной степени в точности. Если нам не удается сделать это точно, то всегда можно сделать приближенно.
Пример:
Требуется начертить квадрат, площадь которого равнялась бы 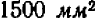 ; какова должна быть в миллиметрах длина его стороны?
; какова должна быть в миллиметрах длина его стороны?
Дело сводится, очевидно, к решению уравнения 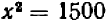 , т. е. к извлечению корня квадратного из
, т. е. к извлечению корня квадратного из 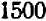 . Мы не найдем целого числа, квадрат которого равнялся бы
. Мы не найдем целого числа, квадрат которого равнялся бы 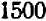 ; но легко убедиться, что квадрат числа
; но легко убедиться, что квадрат числа 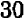 меньше, чем
меньше, чем 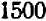 , а квадрат числа
, а квадрат числа 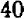 больше, чем
больше, чем 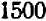 ; точно так же квадрат числа
; точно так же квадрат числа 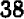 меньше, чем
меньше, чем 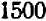 , а квадрат числа
, а квадрат числа 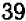 больше, чем
больше, чем 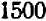 . Отсюда можно заключить, что искомый корень нашего уравнения заключен между
. Отсюда можно заключить, что искомый корень нашего уравнения заключен между 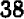 и
и 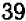 . Он нами вычислен приближенно («с точностью до единицы»). Итак, чтобы начертить квадрат площадью в
. Он нами вычислен приближенно («с точностью до единицы»). Итак, чтобы начертить квадрат площадью в 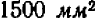 , нужно взять сторону его чуть большей
, нужно взять сторону его чуть большей 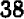 .
.
Предположим, что точность, доставляемая неравенством 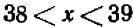 , нас бы не удовлетворяла. Тогда можно было бы перейти хотя бы к десятичным дробям и найти число десятых, содержащихся в искомом числе. Было бы нетрудно установить, что среди чисел
, нас бы не удовлетворяла. Тогда можно было бы перейти хотя бы к десятичным дробям и найти число десятых, содержащихся в искомом числе. Было бы нетрудно установить, что среди чисел 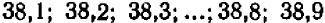 все до числа
все до числа 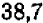 включительно имеют квадраты, меньшие, чем
включительно имеют квадраты, меньшие, чем 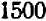 , тогда как два последних имеют квадраты, большие, чем
, тогда как два последних имеют квадраты, большие, чем 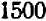 . Отсюда мы заключили бы, что
. Отсюда мы заключили бы, что 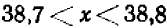 . И так можно было бы продолжать дальше.
. И так можно было бы продолжать дальше.
Знак корня иначе называется радикалом.
Извлечение корней непосредственно н с помощью таблиц
При решении множества самых разнообразных задач приходится извлекать квадратные корни из чисел; довольно часто нужно бывает извлекать и кубические корни.
Иногда удается извлечь корень точно, и притом не прибегая ни к каким особым приемам. Так, например, непосредственно ясно, что:
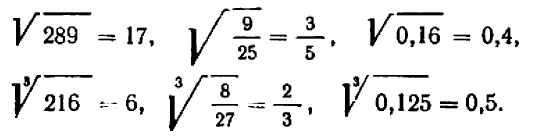
Однако на каждом шагу мы встречаемся и с такими случаями, когда точное извлечение корня не возможно. Тогда, с практической точки зрения, совершенно достаточно найти приближенное значение корня. Обыкновенно значение корня записывают в виде десятичной дроби, ограничиваясь тем или иным числом десятичных знаков после запятой.
Нахождение этих десятичных знаков стоит некоторого труда. Пусть требуется вычислить приближенно 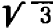 : ото равносильно решению уравнения
: ото равносильно решению уравнения 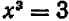 .
.
Легко понять, что искомое число 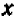 , которое мы обозначаем через
, которое мы обозначаем через 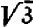 , должно быть больше единицы, но меньше
, должно быть больше единицы, но меньше 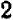 (так как
(так как  , но
, но  ). Уже отсюда ясно, что слева от запятой стоит одна цифра
). Уже отсюда ясно, что слева от запятой стоит одна цифра 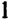 . Чтобы установить следующую цифру, подвергаем испытанию число
. Чтобы установить следующую цифру, подвергаем испытанию число 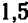 . Так как
. Так как 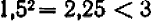 , то число десятых должно быть не меньше, чем
, то число десятых должно быть не меньше, чем 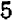 . Попробуем взять число
. Попробуем взять число 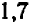 : мы видим, что
: мы видим, что 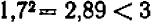 , и потому интересующая нас цифра не меньше, чем
, и потому интересующая нас цифра не меньше, чем 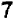 . Испытывая число
. Испытывая число 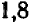 , убеждаемся, что
, убеждаемся, что 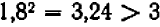 , и, значит, цифра
, и, значит, цифра 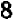 уже слишком велика. Итак, наверное, первая цифра после запятой есть
уже слишком велика. Итак, наверное, первая цифра после запятой есть 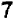 . Чтобы определить вторую цифру, возьмем хотя бы число
. Чтобы определить вторую цифру, возьмем хотя бы число 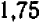 : так как
: так как 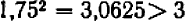 , то мы взяли слишком много. Подставив в уравнение
, то мы взяли слишком много. Подставив в уравнение 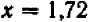 , по лучим
, по лучим 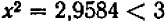 : это — недостаточно. Дальше,
: это — недостаточно. Дальше, 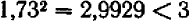 : тоже мало. Но
: тоже мало. Но 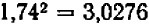 — уже больше, чем нужно. Теперь нет сомнения в том, что вторая цифра после запятой есть
— уже больше, чем нужно. Теперь нет сомнения в том, что вторая цифра после запятой есть 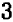 . Можно сказать, что искомый корень
. Можно сказать, что искомый корень 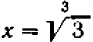 приближенно, с точностью до одной сотой, равен
приближенно, с точностью до одной сотой, равен 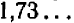 Если нужна большая точность, то таким же методом, с помощью дальнейших «проб», найдем и третий десятичный знак после запятой.
Если нужна большая точность, то таким же методом, с помощью дальнейших «проб», найдем и третий десятичный знак после запятой.
То же можно сказать и о вычислении корней кубических. Желая, например, определить приближенное значение 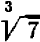 , т. е. найти приближенное решение уравнения
, т. е. найти приближенное решение уравнения 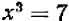 , мы в результате «проб» (затратив порядочно времени) придем к заключению, что
, мы в результате «проб» (затратив порядочно времени) придем к заключению, что 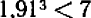 , но
, но 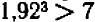 ; отсюда следует, что
; отсюда следует, что 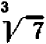 приближенно равняется
приближенно равняется 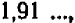 причем можно ручаться за правильность всех выписанных цифр.
причем можно ручаться за правильность всех выписанных цифр.
Более усовершенствованный прием извлечения корня (квадратного) указывается в основном курсе алгебры. С другой стороны, в особенности, если надо извлечь целый ряд корней, естественно прибегнуть к готовым таблицам. Существуют таблицы корней с четырьмя, пятью, десятью и большим числом десятичных знаков.
Можно себе представить, какой громадный труд был вложен при составлении этих таблиц, иногда издаваемых в виде отдельных книжек.
Для целей курса начальной алгебры достаточны трехзначные таблицы, внимающие гораздо меньше места. Такие таблицы при ведены в конце этой книги.
Следует заметить, что они составлены посредством округления до ближайшей тысячной тех данных, которые содержатся в более подробных таблицах. Поэтому погрешность, возникающая при заимствовании числового значения корня из таблиц этой книги, не может превысить половины тысячной, т. е.  .
.
Понятие об алгебраических корнях
Извлекая корень квадратный из какого-нибудь числа, например 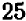 , мы ставим себе задачу — решить уравнение
, мы ставим себе задачу — решить уравнение 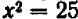 , т. е. найти все числа, квадрат которых равен
, т. е. найти все числа, квадрат которых равен 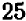 . Решение существует: уравнение имеет корень
. Решение существует: уравнение имеет корень 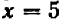 . Но этот корень — не единственный: противоположное по знаку число
. Но этот корень — не единственный: противоположное по знаку число 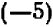 также удовлетворяет требованию:
также удовлетворяет требованию: 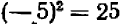 .
.
Можно было бы рассуждать иначе: придав уравнению вид 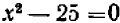 , или
, или 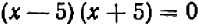 , и принимая во внимание, что произведение может равняться нулю только в том случае, если один из множителей равен нулю, мы видим, что неизвестное
, и принимая во внимание, что произведение может равняться нулю только в том случае, если один из множителей равен нулю, мы видим, что неизвестное 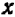 или равно
или равно 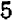 , или
, или 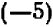 — третьего корня нет.
— третьего корня нет.
Таким же образом, всякое положительное число имеет два корня квадратных: один корень — положительный, другой — противоположный по знаку, отрицательный. Пишут иногда: 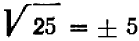 ,
, 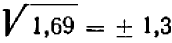 и т. п.
и т. п.
Положительное значение корня квадратного называется арифметическим (или значением корня в арифметическом смысле).
Напротив, если хотят рассматривать оба значения квадратного корня из положительного числа, то говорят об алгебраических значениях корня (или о значениях корня в алгебраическом смысле).
Из отрицательного числа квадратный корень извлечь нельзя; действительно, квадрат никакого числа не может быть отрицательным. Другими словами, отрицательные числа квадратных корней не имеют.
Что касается нуля, то легко понять, что корень квадратный из  существует только один:
существует только один: 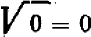 .
.
В таблицах ради краткости указываются только арифметические (т. е. положительные) значения корней.
Полезно уяснить себе геометрическую сторону дела, добавляя к графику уравнения 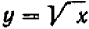 (см. упр. 230, пункт 699) те точки, которые соответствуют отрицательным значениям радикалов.
(см. упр. 230, пункт 699) те точки, которые соответствуют отрицательным значениям радикалов.
Предыдущие замечания относятся только к корням квадратным, но не кубическим. Так как куб всякого положительного числа есть число положительное, а куб всякого-отрицательного числа — число отрицательное, то и обратно: корень кубический из положительного числа имеет лишь одно значение — положительное, а корень кубический из отрицательного числа — лишь одно значение, отрицательное.
Например: 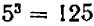 ,
, 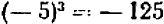 , поэтому
, поэтому 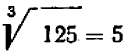 ,
, 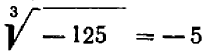 .
.
К тому же результату приводит иное рассуждение. Уравнению 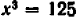 можно придать вид
можно придать вид 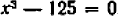 , или
, или 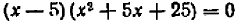 .
.
Второй множитель не может равняться нулю, так как при любом значении 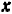
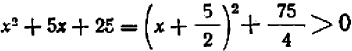 и значит, должен быть равен нулю первый множитель, что дает
и значит, должен быть равен нулю первый множитель, что дает  .
.
Глядя на график уравнения кубической параболы совсем не трудно «прочесть» ответ на вопрос: сколько существует корней кубических из данного, положительного или отрицательного, числа.
Нахождение промежуточных значений по таблице
Указание. Написав уравнение прямой линии в форме 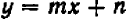 , следует подобрать коэффициенты
, следует подобрать коэффициенты 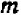 и
и 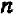 таким образом, чтобы уравнению удовлетворяли координаты точек
таким образом, чтобы уравнению удовлетворяли координаты точек 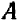 и
и 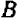 . Затем, подставив в уравнение найденные значения
. Затем, подставив в уравнение найденные значения 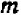 и
и 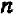 , останется только вычислить значения
, останется только вычислить значения 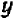 при х = 6.
при х = 6.
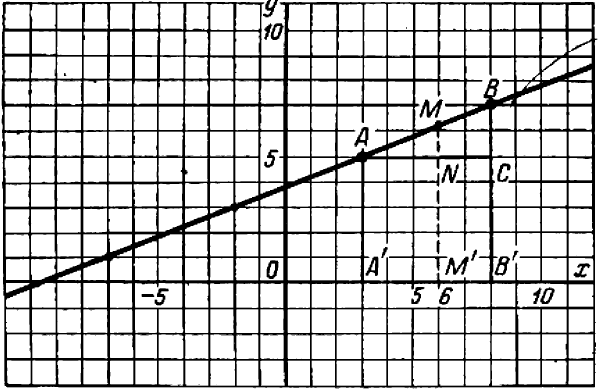
Как ни просто указанное решение этой задачи, при необходимости решать большое число задач подобного содержания удобнее рассуждать несколько иначе. Именно, достаточно прибегнуть к составлению про порции. Из чертежа видно, что в треугольниках 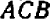 и
и 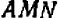 катеты
катеты 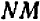 и
и 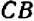 пропорциональны катетам
пропорциональны катетам 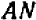 и
и 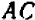 :
: 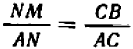 .
.
В этой пропорции известны все члены, кроме первого; в самом деле: 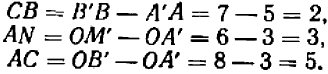
Поэтому пропорция принимает вид 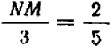 и отсюда следует:
и отсюда следует: 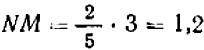 ,
, 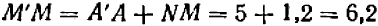 .
.
Короче: если на 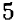 единиц «приращения абсциссы
единиц «приращения абсциссы 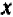 » (
» (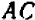 ) приходится
) приходится 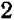 единицы «приращения ординаты» (
единицы «приращения ординаты» (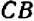 ), то на
), то на 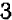 единицы «приращения абсциссы
единицы «приращения абсциссы 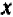 » (
» (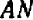 ) придется —
) придется — 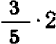 , т. е.
, т. е. 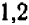 «приращения ординаты» (
«приращения ординаты» (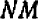 ); итого, искомая ордината равна «начальной» (
); итого, искомая ордината равна «начальной» (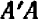 ) плюс «приращение» (
) плюс «приращение» (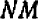 ):
): 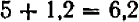 .
.
При нахождении корня квадратного или кубического из числа, которое отсутствует в таблице, но заключено между двумя числами, имеющимися в таблице, приходится решать подобные же задачи. Правда, таблица составлена не для линейной зависимости, и, следовательно, график ее — не прямая линия; тем не менее на очень маленьком протяжении (между точками, абсциссы которых равны последовательно взятым числам таблицы) кривую приближенно можно заменить прямой линией и зависимость между 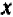 и
и 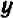 считать линейной.
считать линейной.
Пример:
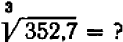
В таблице находим: 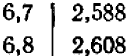
При увеличении числа па 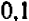 корень из него увеличивается на
корень из него увеличивается на 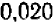 . Отсюда следует, что при увеличении числа на
. Отсюда следует, что при увеличении числа на 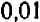 корень увеличивается на
корень увеличивается на 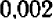 ; а при увеличении на
; а при увеличении на 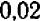 корень должен увеличиться на
корень должен увеличиться на 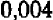 . Итак, можно считать, что
. Итак, можно считать, что 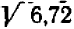 равняется
равняется 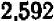 .
.
Пример:
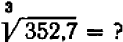
В таблице находим: 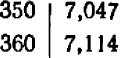
Запишем кратко приращения:  (округлено в тысячных)
(округлено в тысячных)
Итак, 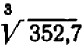 равняется
равняется 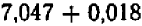 , т. е.
, т. е. 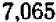 .
.
Полезно постепенно научиться проделывать подобного рода вычисления в уме.
Употребление таблиц при решении простейших геометрических задач
Примечание:
Пользуясь в дальнейшем таблицами корней квадратных и кубических, следует округлять данные и результаты до трех значащих цифр.
Приближенное определение корней уравнения
Пусть дано уравнение второй степени (квадратное уравнение) 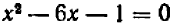 .
.
Пробуя разыскать его решение непосредственными подстановками, мы замечаем, что его левая часть (которую мы обозначим через 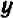 )
) 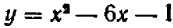 при значениях
при значениях 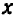 , равных
, равных 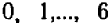 , принимает отрицательные значения, но при значениях
, принимает отрицательные значения, но при значениях 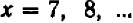 принимает значения положительные
принимает значения положительные 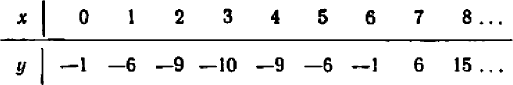
Соответствующий график намечен на черт. 56.
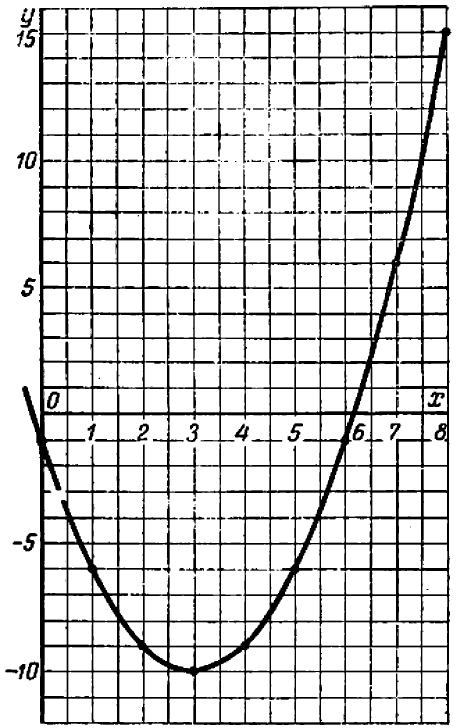
Возникает мысль, что при переходе от точки 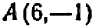 к точке
к точке 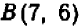 кривая должна в какой-то точке, абсцисса которой заключена между
кривая должна в какой-то точке, абсцисса которой заключена между 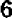 и
и 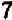 , пересечь ось
, пересечь ось 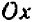 ; другими словами, величина
; другими словами, величина 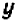 должна принять значение
должна принять значение  , т. е. уравнение
, т. е. уравнение 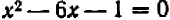 должно иметь корень в промежутке
должно иметь корень в промежутке 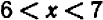 . Более точно этот корень можно вычислить уже знакомыми нам приемами. Подставляя хотя бы значение
. Более точно этот корень можно вычислить уже знакомыми нам приемами. Подставляя хотя бы значение 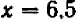 , мы убеждаемся, что при этом значении величина
, мы убеждаемся, что при этом значении величина 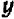 принимает уже положительное значение
принимает уже положительное значение 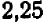 ; отсюда можно заключить, что перемена знака
; отсюда можно заключить, что перемена знака 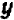 совершается в промежутке, более тесном
совершается в промежутке, более тесном 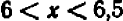 . Подставляя
. Подставляя 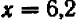 , получаем
, получаем 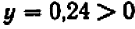 , и промежуток снова стеснился:
, и промежуток снова стеснился: 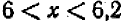 . Наконец, подстановка
. Наконец, подстановка 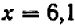 дает:
дает: 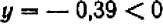 ; итак, искомый корень уравнения находится в промежутке
; итак, искомый корень уравнения находится в промежутке 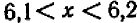 . Таким образом, значение корня уже известно с точностью до одной десятой. Так называется это уравнение потому, что в нем отсутствует член первой степени.
. Таким образом, значение корня уже известно с точностью до одной десятой. Так называется это уравнение потому, что в нем отсутствует член первой степени.
Подставляя дальше промежуточные значения 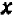 , заключенные между
, заключенные между 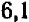 и
и 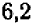 , мы сможем вычислить корень с точностью до одной сотой и т. д.
, мы сможем вычислить корень с точностью до одной сотой и т. д.
Применение радикалов к решению квадратных уравнений с числовыми коэффициентами
Рассмотрим неполное квадратное уравнение 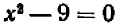 и постараемся найти все его корни. Сделать это очень легко, если преобразовать левую часть по формуле «разность квадратов» :
и постараемся найти все его корни. Сделать это очень легко, если преобразовать левую часть по формуле «разность квадратов» : 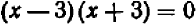 .
.
Дальше придется сказать: «Произведение равняется нулю в том, и только в том случае, если один из множителей равен нулю». В данном примере может быть одно из двух: или 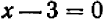 , или
, или 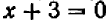 .
.
Но в первом случае 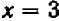 , во вторам
, во вторам 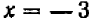 .
.
Итак, наше уравнение имеет точно два корня: 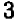 и
и 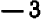 .
.
Если бы было дано квадратное уравнение 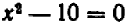 , то в предыдущем рассуждении изменялось бы немногое: нужно было бы принять во внимание, что
, то в предыдущем рассуждении изменялось бы немногое: нужно было бы принять во внимание, что 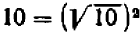 , и тогда мы получили бы
, и тогда мы получили бы 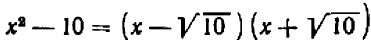 . Отсюда можно было бы заключить о существовании двух корней уравнения, а именно,
. Отсюда можно было бы заключить о существовании двух корней уравнения, а именно, 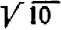 и
и 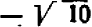 .
.
Рассмотрим теперь полное квадратное уравнение, например, 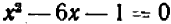
Его решение не представит труда, если удастся разложить на линейные множители левую часть. Для разложения трехчлена второй степени на линейные множители существует замечательный прием, который носит название «выделение квадрата».
В формуле «квадрат суммы» 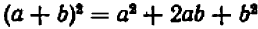 положим
положим  ,
, 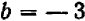 , и тогда получим
, и тогда получим 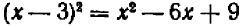 .
.
Последнее выражение только свободным членом отличается от левой части данного уравнения 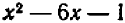 . Если добавим свободный член
. Если добавим свободный член 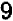 , то, чтобы тождество не было нарушено, придется одновременно
, то, чтобы тождество не было нарушено, придется одновременно 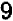 отнять:
отнять: 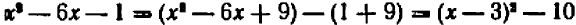 .
.
Итак, наш трехчлен принимает вид  ,
,
или 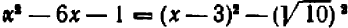 . Теперь уже ничего не стоит разложить трехчлен на множители:
. Теперь уже ничего не стоит разложить трехчлен на множители:
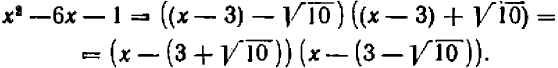
После того уравнение можно переписать в следующей форме 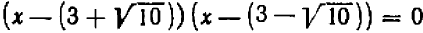 , и прежнее рассуждение приводит к заключению, что данное уравнение имеет два корня:
, и прежнее рассуждение приводит к заключению, что данное уравнение имеет два корня: 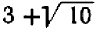 и
и 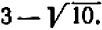 .
.
Обращаясь к таблицам, видим, что эти корни приближенно равны 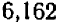 и
и 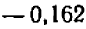 .
.
Если коэффициент при старшем члене в данном трехчлене неравен единице единице, то лучше всего при разложении трехчлена на множители сразу выносить его за скобки. Например, 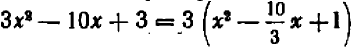 .
.
Но 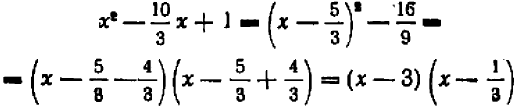 .
.
Значит, 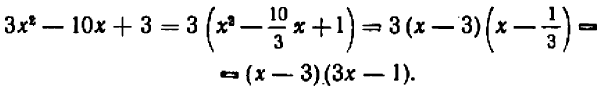
Некоторые действия с радикалами
Выполняя те или иные действия над радикалами, необходимо прежде всего помнить, что согласно смыслу радикала имеют место тождества 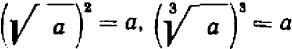 или
или 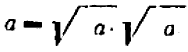 ,
, 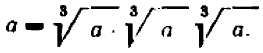
Предполагая числа 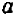 и
и 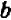 положительными, а все входящие корни считая арифметическими, установим справедливость следующих формул (I—IV):
положительными, а все входящие корни считая арифметическими, установим справедливость следующих формул (I—IV):
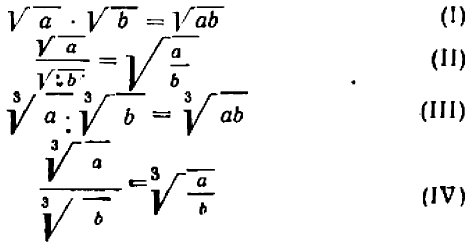
Чтобы убедиться в справедливости paвенств (I), посмотрим, каковы квадраты выражений 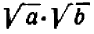 ,
, 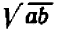 .
.
Мы получаем: 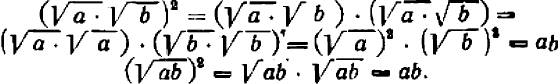
Оказывается, что положительные числа 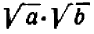 и
и 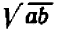 имеют одинаковые квадраты, именно,
имеют одинаковые квадраты, именно, 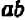 . Значит, они оба являются корнями квадратными из числа
. Значит, они оба являются корнями квадратными из числа 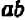 .
.
Но так как каждое положительное число имеет только один положительный квадратный корень, то отсюда следует, что рассматриваемые числа не могут быть различными. Таким же образом устанавливается справедливость равенства (П).
Что касается равенств (III) и (IV), то для их доказательства нужно, конечно, сравнить между собой не квадраты, а кубы правой н левой частей, ссылаясь на то, что каждое положительное число имеет только один кубический корень.
Упомянутые свойства не являются для нас новыми. Нам уже известно, что если  и
и  , то
, то  . В частности, полагая
. В частности, полагая 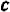 равным
равным 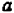 и
и 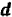 равным
равным 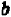 , мы получим первое из свойств. Полагая
, мы получим первое из свойств. Полагая 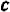 равным
равным 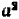 и
и 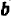 равным
равным 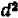 , получим второе.
, получим второе.
При решении уравнений, содержащих радикалы, необходимо делать проверку.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

