Геометрическая прогрессия в математике с примерами решения и образцами выполнения

Оглавление:

Определение геометрической прогрессии:

Рассмотрим последовательность, членами которой являются степени числа 2 с натуральными показателями:

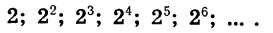
Каждый член этой последовательности, начиная со второго, получается умножением предыдущего члена на 2. Эта последовательность является примером геометрической прогрессии.

Определение:

Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.

Иначе говоря, последовательность 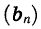— геометрическая прогрессия, если для любого натурального п выполняются условия

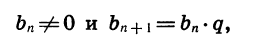
где q — некоторое число. Обозначим, например, через 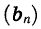Геометрическая прогрессия последовательность натуральных степеней числа 2. В этом случае для любого натурального п верно равенство 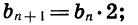здесь q = 2.

Из определения геометрической прогрессии следует, что отношение любого ее члена, начиная со второго, к предыдущему члену равно q, т. е. при любом натуральном n верно равенство

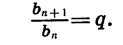
Число q называют знаменателем геометрической прогрессии.

Очевидно, что знаменатель геометрической прогрессии отличен от нуля.

Чтобы задать геометрическую прогрессию, достаточно указать ее первый член и знаменатель.

Приведем примеры.

Если 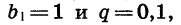Геометрическая прогрессия то получим геометрическую прогрессию

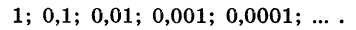
Условиями 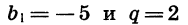задается геометрическая прогрессия

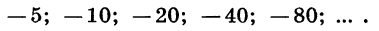
Если 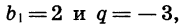Геометрическая прогрессия то имеем прогрессию

Если 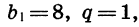Геометрическая прогрессия то получим геометрическую прогрессию

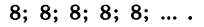
Зная первый член и знаменатель геометрической прогрессии, можно найти последовательно второй, третий и вообще любой ее член:

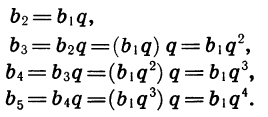
Точно так же находим, что 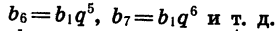Геометрическая прогрессия Вообще, чтобы найти 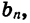мы должны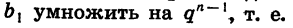

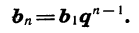
Мы получили формулу n-го члена геометрической прогрессии.

Приведем примеры решения задач с использованием этой формулы.

Пример:

В геометрической прогрессии 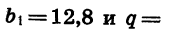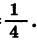Геометрическая прогрессия Найдем b7.

По формуле n-го члена геометрической прогрессии

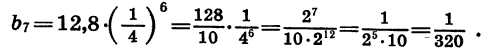
Пример:

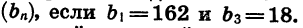
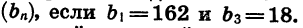
Найдем восьмой член геометрической прогрессии Геометрическая прогрессия

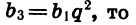
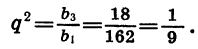
Зная первый и третий члены геометрической прогрессии, можно найти ее знаменатель. Так как Геометрическая прогрессия

Решив уравнение

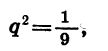
найдем, что

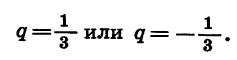
Таким образом, существуют две прогрессии, удовлетворяющие условию задачи.

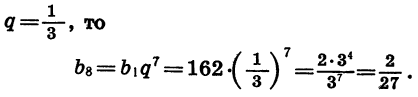
Если

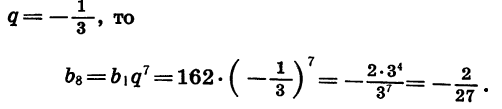
Задача имеет два решения:

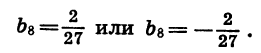
Пример:

После каждого движения поршня разрежающего насоса из сосуда удаляется 20% находящегося в нем воздуха. Определим давление воздуха внутри сосуда, после шести движений поршня, если первоначально давление было 760 мм рт. ст.

Так как после каждого движения поршня из сосуда удаляется 20% имевшегося воздуха, то остается 80% воздуха. Чтобы узнать давление воздуха в сосуде после очередного движения поршня, нужно давление после предыдущего движения поршня умножить на 0,8.

Мы имеем геометрическую прогрессию, первый член которой равен 760, а знаменатель равен 0,8. Число, выражающее давление воздуха в сосуде (в мм рт. ст.) после шести движений поршня, является седьмым членом этой прогрессии. Оно равно

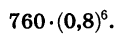
Произведя вычисления, получим:

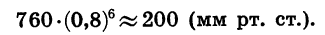
Формула суммы n первых членов геометрической прогрессии

Древняя индийская легенда рассказывает, что изобретатель шахмат попросил в награду за свое изобретение столько пшеничных зерен, сколько их получится, если на первую клетку шахматной доски положить одно зерно, на вторую — в 2 раза больше, т. е. 2 зерна, на третью — еще в 2 раза больше, т. е. 4 зерна, и т. д. до 64-й клетки. Сколько зерен должен был получить изобретатель шахмат?

Число зерен, о которых идет речь, является суммой шестидесяти четырех членов геометрической прогрессии, первый член которой равен 1, а знаменатель равен 2. Обозначим эту сумму через S:

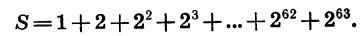
Умножим обе части записанного равенства на знаменатель прогрессии, получим:

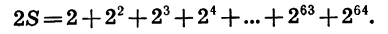
Вычтем почленно из второго равенства первое и проведем упрощения:

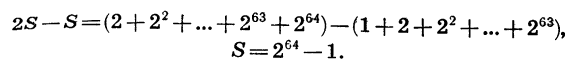
Можно подсчитать, что масса такого числа пшеничных зерен больше триллиона тонн. Это заведомо превосходит количество пшеницы, собранной человечеством до настоящего времени.

Выведем теперь формулу суммы n первых членов произвольной геометрической прогрессии. Воспользуемся тем же приемом, с помощью которого была вычислена сумма S.

Пусть дана геометрическая прогрессия 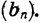Обозначим сумму n первых ее членов через :

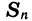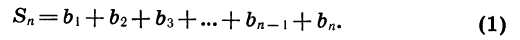
Умножим обе части этого равенства на q:

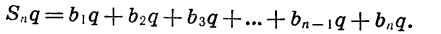
Учитывая, что

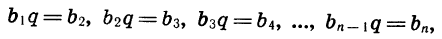
получим:

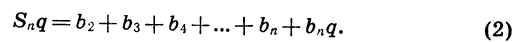
Вычтем почленно из равенства (2) равенство (1) и приведем подобные члены:

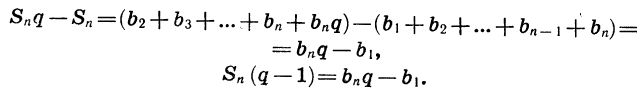
Отсюда следует, что при 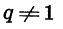Геометрическая прогрессия

Мы получили формулу суммы n первых членов геометрической прогрессии, в которой 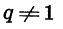Геометрическая прогрессия . Если q = 1, то все члены прогрессии равны первому члену и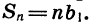

При решении многих задач удобно пользоваться формулой суммы п первых членов геометрической прогрессии, записанной в другом виде. Подставим в формулу (I) вместо 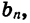Геометрическая прогрессия выражение 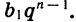Получим:

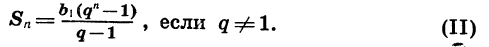
Пример:

Найдем сумму первых десяти членов геометрической прогрессии 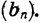Геометрическая прогрессия в которой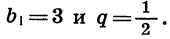

Так как известны первый член и знаменатель прогрессии, то удобно воспользоваться формулой (II). Получим:

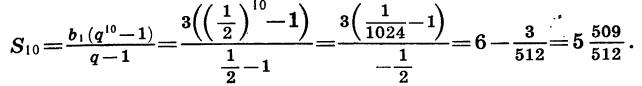
Пример:

Найдем сумму 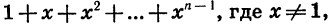Геометрическая прогрессия слагаемые которой являются последовательными членами геометрической прогрессии

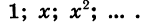
Первый член прогрессии равен 1, а знаменатель равен х. Так как 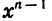Геометрическая прогрессия является членом этой прогрессии с номером n, то задача состоит в нахождении суммы п первых ее членов. Воспользуемся формулой (I):

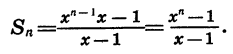
Таким образом, если 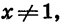Геометрическая прогрессия то

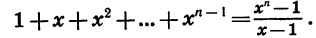
Умножив левую и правую части последнего равенства на х — 1, получим тождество

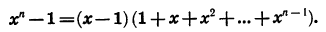
В частности, при n = 2 и n = 3 приходим к известным формулам

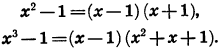
Пример:

Найдем сумму шести первых членов геометрической прогрессии 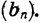Геометрическая прогрессия если известно, что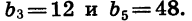

Зная 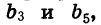Геометрическая прогрессия можно найти знаменатель прогрессии q. Так как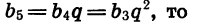

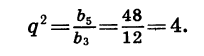
Значит,

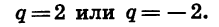
Таким образом, существуют две прогрессии, удовлетворяющие условию задачи.

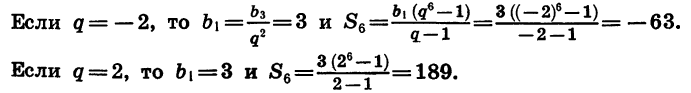
Сумма бесконечной геометрической прогрессии при |q|< 1

Пусть длина отрезка АВ равна 2 ед. (рис. 50). Отметим точку В1 — середину отрезка А В, затем точку В2 — середину правой его половины, затем точку В3 — середину получившегося справа отрезка и т. д. Длины отрезков 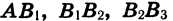Геометрическая прогрессия и т. д. образуют бесконечную геометрическую прогрессию, знаменатель которой равен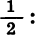

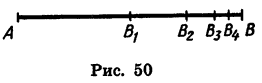
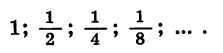
Найдем сумму n первых членов этой прогрессии:

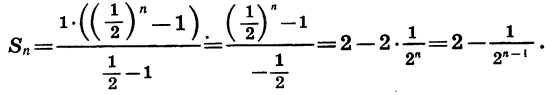
При увеличении числа слагаемых n значение дроби 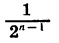Геометрическая прогрессия приближается к нулю. Действительно,

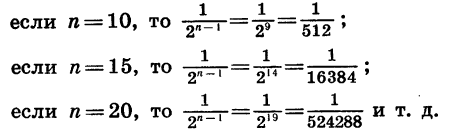
Поэтому при неограниченном увеличении n разность 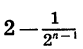Геометрическая прогрессия становится сколь угодно близкой к числу 2 или, как говорят, стремится к числу 2.

Таким образом, сумма n первых членов геометрической прогрессии 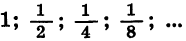Геометрическая прогрессия при неограниченном увеличении n стремится к числу 2. Число 2 называют суммой бесконечной геометрической прогрессии 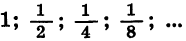и пишут:

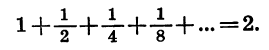
Это равенство легко истолковать геометрически: сумма длин отрезков 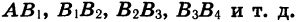Геометрическая прогрессия равна длине отрезка АВ.

Рассмотрим теперь произвольную геометрическую прогрессию

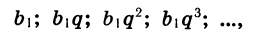
у которой |q|< 1

Запишем формулу суммы п первых членов прогрессии:

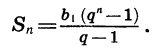
Преобразуем выражение в правой части равенства:

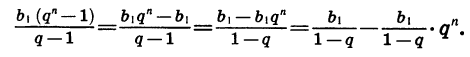
Значит,

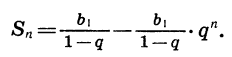
Можно доказать, что если 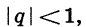Геометрическая прогрессия то при неограниченном увеличении n множитель 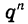стремится к нулю, а значит, стремится к нулю и произведение 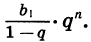Поэтому при неограниченном увеличении n сумма Sn стремится к числу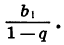 Геометрическая прогрессия

Число 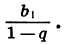Геометрическая прогрессия называют суммой бесконечной геометрической прогрессии 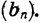у которой

Это записывают так:

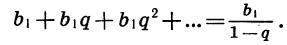
Обозначив сумму прогрессии 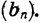Геометрическая прогрессия буквой S, получим формулу

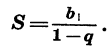
Заметим, что если 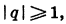то сумма n первых членов геометрической прогрессии при неограниченном увеличении n не стремится ни к какому числу. Бесконечная геометрическая прогрессия имеет сумму только при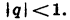

Пример:

Найдем сумму бесконечной геометрической прогрессии 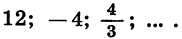Геометрическая прогрессия

У этой прогрессии 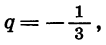Геометрическая прогрессия значит, условие |q| < 1 выполнено. По формуле 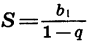получим:

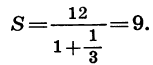
Пример:

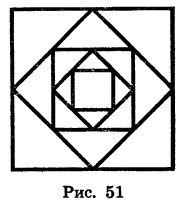
Дан квадрат, сторона которого равна 4 см. Середины его сторон являются вершинами второго квадрата, середины сторон второго квадрата являются вершинами третьего квадрата и т. д. (рис. 51). Найдем сумму площадей всех квадратов.

Из геометрических соображений ясно, что площадь каждого следующего квадрата равна половине площади предыдущего. Таким образом, последовательность площадей квадратов является геометрической прогрессией, первый член которой равен 16, а знаменатель равен 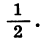Геометрическая прогрессия Найдем сумму этой геометрической прогрессии:

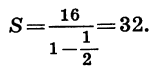
Значит, сумма площадей всех квадратов равна 32 см2.

Из курса VIII класса нам известно, что каждое рациональное число может быть представлено в виде бесконечной десятичной периодической дроби. Чтобы выразить рациональное число 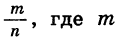Геометрическая прогрессия — целое число, а n — натуральное, в виде бесконечной десятичной дроби, достаточно разделить числитель на знаменатель. Наоборот, каждая бесконечная десятичная периодическая дробь представляет некоторое рациональное число. Покажем на примере, как с помощью формулы суммы бесконечной геометрической прогрессии можно представить бесконечную десятичную периодическую дробь в виде отношения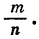 Геометрическая прогрессия

Пример:

Представим бесконечную десятичную периодическую дробь 0,(18) в виде обыкновенной дроби.

По аналогии с конечными десятичными дробями представим бесконечную десятичную дробь 0,(18) в виде суммы:

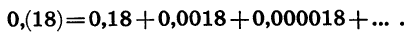
Слагаемые в правой части равенства — члены геометрической прогрессии, у которой первый член равен 0,18, а знаменатель равен 0,01, т. е. условие 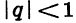Геометрическая прогрессия выполнено. Найдем сумму этой прогрессии:

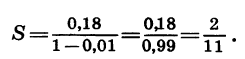
Значит,

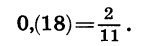
Таким же способом можно представить в виде обыкновенной дроби любую бесконечную десятичную периодическую дробь.

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике: