Тригонометрические функции числового аргумента и их графики в математике с примерами решения и образцами выполнения

Определение:

В настоящей главе мы введем тригонометрические функции числового аргумента. Многие вопросы математики, механики, физики и других наук приводят к тригонометрическим функциям не только угла (дуги), но и аргументов совершенно различной природы (длина, время, температура и т. д.). До сих пор под аргументом тригонометрической функции понимался угол, измеренный в градусах или радианах. Теперь мы обобщим понятия синуса, косинуса, тангенса, котангенса, секанса и косеканса, введя их как функции числового аргумента.

Определение:

Тригонометрическими функциями числового аргумента х называются одноименные тригонометрические функции угла, равного х радианам.

Поясним это определение на конкретных примерах.

Пример:

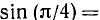
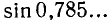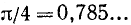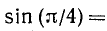
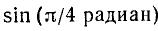
Вычислим значенйе . Здесь под мы понимаем отвлеченное иррациональное число. Согласно определению 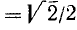. Итак, .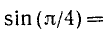

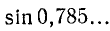
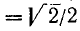Пример:

Вычислим значение sin 1,5. Здесь под 1,5 мы понимаем отвлеченное число. Согласно определению sin 1,5 = sin (1,5 радиана) = 0,9975 (см. приложение II).

Пример:

Вычислим значение tg 1,3. Аналогично предыдущему получаем tg 1,3 = tg (1,3 радиана) = 3,6021 (см. приложение II).

Итак, в дальнейшем под аргументом тригонометрических функций мы будем понимать угол (дугу) или просто число в зависимости от той задачи, которую решаем. А в ряде случаев аргументом может служить величина, имеющая и другую размерность, например время и т. д. Называя аргумент углом (дугой), мы можем подразумевать под ним число, с помощью которого он измерен в радианах. Например, вместо слов «косинус числа 10» будем говорить «косинус угла, равного 10 радианам».

Области определения и области изменения значений тригонометрических функций

Уточним области определения (существования) и области изменения значений тригонометрических функций, рассматриваемых как функции числового аргумента (х — число). Здесь мы существенным образом воспользуемся результатами пп. 97, 98.

1) y = sin x. Так как соответствующая функция угла определена для всех углов х, то и новая функция определена для Есех действительных чисел х (—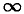 < х < + 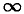). Синус как функция угла изменяется в пределах от —1 до +1, следовательно, и новая функция изменяется в пределах от —1 до +1, т. е. она удовлетворяет неравенствам 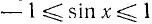. (Область изменения значений функции sin x — отрезок [—1, 1] оси Оу.)

Для остальных функций сообщаем просто результаты. Рассуждения аналогичны предыдущему.

2) y = cos х. Область определения (существования): —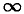 < х < +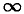. Область измеиения функции: .

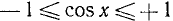3) у = tg x. Область определения (существования): х — любое действительное число, кроме чисел вида 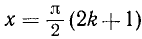, где k = 0, ±1, ±2, … .

Область изменения функции: —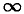 < tg x < +.

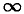4) у = ctg x. Область определения (существования): х —любое действительное число, кроме чисел вида 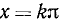, где k = ±1, ±2, … . Область изменения функции: — 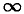< ctg x < +.

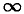Заметим, что все свойства тригонометрических функций угла (четность, нечетность, периодичность) переносятся на тригонометрические функции числового аргумента.

Некоторые неравенства и их следствия

Выведем теперь некоторые неравенства и их следствия.

Неравенство 1. Для всех действительных значений х, удовлетворяющих неравенствам 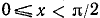, справедливы следующие неравенства:

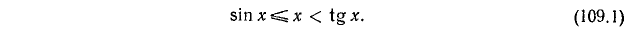
Доказательство:

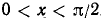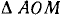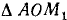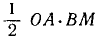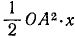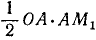Пусть число x удовлетворяет неравенствам . Построим окружность радиуса OA = 1 и в ней отложим от оси Ох центральный угол АОМ, равный х радианам (рис. 111). Из чертежа видно, что площадь меньше площади сектора АОМ, которая меньше площади . Соответствующие площади равны , и . Следовательно,

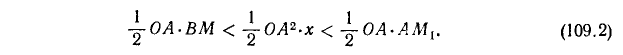
Так как 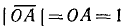, то 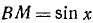, , 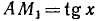и неравенства (109.2) принимают вид

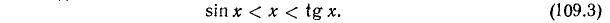
Заметив, что sin 0 = tg 0 = 0, приходим к неравенствам (109.1).

Неравенство 2. Для всех действительных значений х справедливо неравенство

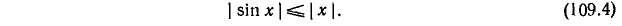
(Абсолютная величина функции sin x не превосходит абсолютной величины ее аргумента.)

Доказательство:

1) Если 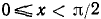, то неравенство (109.4) справедливо на основании (109.1).

2) Если 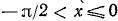, то, сделав замену переменной х на у по формуле у = — х, получим sin у = sin (— х) = —sin х, где у уже удовлетворяет неравенствам 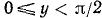, и для него справедливы неравенства 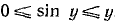. Вернувшись к переменной х, получим или 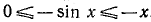. Последние неравенства равносильны неравенству 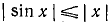либо .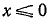

3) Если же 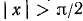, то и подавно 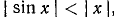, так как .

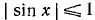Итак, мы доказали, что для всех действительных значений х справедливо неравенство (109.4).

Заметим, что только при х = 0 мы имеем равенство sin 0 = 0.

Неравенство 3. Для всех действительных значений х справедливы неравенства

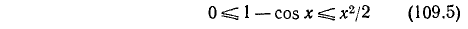
и, следовательно, неравенство

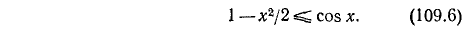
Доказательство:

По формуле (121.3) (см. стр. 306) имеем

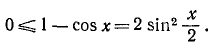
На основании неравенства (109.4) можем писать 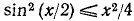. Таким образом,

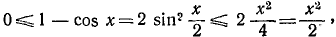
что и требовалось доказать.

Из (109.5) получим

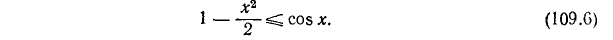
С помощью полученных неравенств изучим поведение cos x, sin x и tg x при малых х.

Следствие:

При малых х

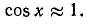
Доказательство:

На основании (109.5) имеем 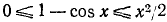, а это и значит, что 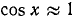при малых х, причем ошибка, которую мы допускаем при замене cos х на 1, не превосходит .

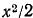Пример:

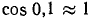, причем .

Пример:

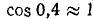, причем .

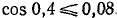Следствие:

При малых х

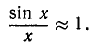
Доказательство:

Пусть 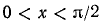; тогда на основании (109.3) имеем

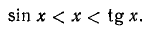
Разделим теперь sin х на каждый из членов последних неравенств; получим

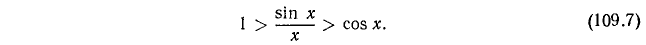
Умножим все члены неравенств (109.7) на —1; получим

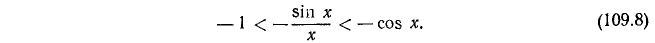
Затем ко всем членам последних неравенств прибавим по единице, получим

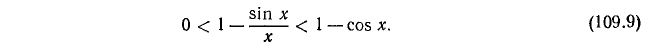
Применив теперь одно из неравенств (109.5), получим

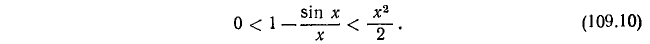
Мы вывели (109.10) в предположении, что 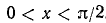. Рекомендуем читателю доказать самостоятельно, что (109.10) имеет место и при 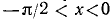. Итак, при х, удовлетворяющих условию 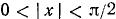, справедливы неравенства (109.10). А это и значит, что 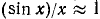, т. е. 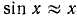, причем ошибка, которую мы допускаем при замене sin x на х, не превосходит 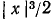. (Из (109.10) имеем )

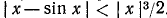Пример:

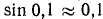, причем .

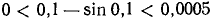Пример:

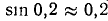, причем .

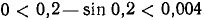Графики тригонометрических функций

Первоначальные сведения о таблицах тригонометрических функций: В Приложениях к настоящей книге приведены таблицы, которые дают возможность получить значения основных тригонометрических функций с четырьмя значащими цифрами.

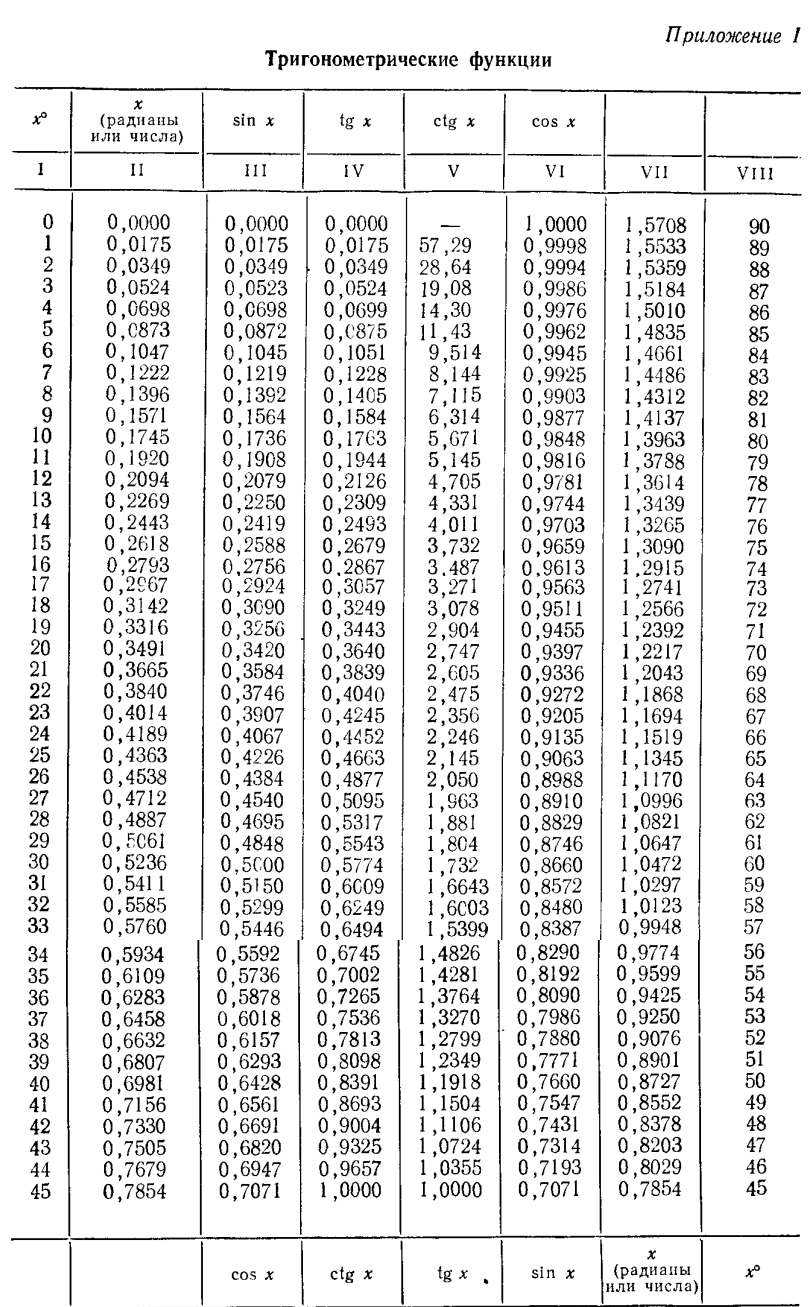
Приложение I. Таблица составлена для значений аргумента х в градусной мере. В графе I даются значения аргумента х° с шагом в 1° от 0° до 45°. В графе II даются соответствующие значения угла в радианной мере. Этой же графой можно пользоваться для отыскания значений тригонометрических функций числового аргумента (см. п. 107). В графах III—VI даются соответственно значения тригонометрических функций— значения sin x, tg x, ctg x и cos x, если 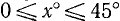, и даются значения cos x, ctg x, tg x и sin x, если 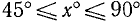(читай внизу!). Тригонометрические функции остальных углов можно уже искать, используя всевозможные формулы приведения (см. п. 106). В графе VIII даются значения аргумента х° с шагом в 1° от 45° до 99° (читай снизу вверх!). В графе VII даются соответствующие значения угла в радианной мере (или просто числа!).

Поясним, как можно пользоваться таблицей. Итак, считаем, что, использовав соответствующие формулы приведения, мы пришли к отысканию тригонометрической функции неотрицательного угла, не большего 90°.

Пример:

Найти tg 39°.

В графе I находим число 39. В графе IV (угол меньше 45°) находим соответствующее ему значение tg 39°, равное 0,8098. Итак, tg 39° — 0,8098.

Пример:

Найти tg 62°.

В графе VIII находим число 62. В графе V (угол больше 45°) находим соответствующее ему значение tg 62°, равное 1,881. Итак, tg 62° — 1,881.

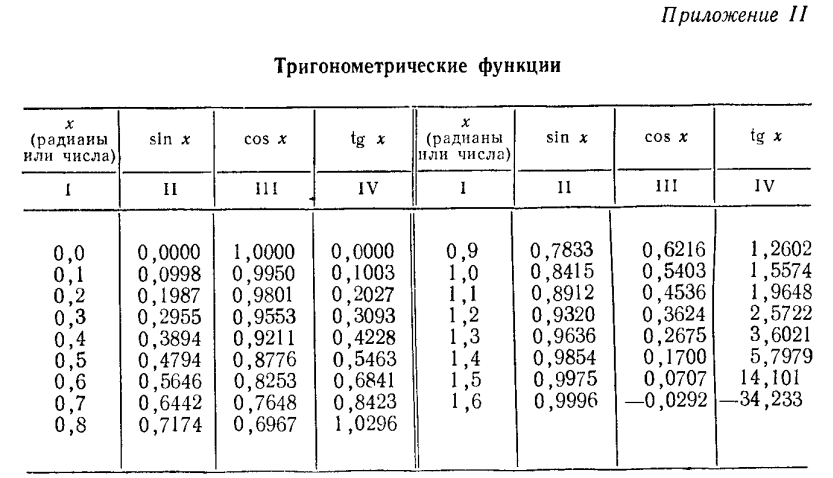
Приложение II. Таблица составлена для значений х в радианной мере. В графе I даются значения аргумента х с шагом 0,1 от 0 до 1,6. В графах II—IV даются соответственно значения тригонометрических функций—значения sin x, cos x и tg x. Этой же таблицей можно пользоваться для отыскания значений тригонометрических функций числового аргумента (см. п. 107).

Тригонометрические функции остальных углов можно искать, используя всевозможные формулы приведения (см. п. 106).

Итак, допустим, что, использовав соответствующие формулы приведения, мы пришли к отысканию тригонометрической функции неотрицательного угла, не большего 1,6.

Пример:

Найти cos 0,7.

В графе I находим число 0,7. В графе III находим соответствующее ему значение cos 0,7, равное 0,7648. Итак, cos 0,7 = 0,7648.

Пример:

Найти tg l,4.

В графе I находим число 1,4. В графе IV находим соответствующее ему значение tg l,4, равное 5,7979. Итак, tg 1,4 = 5,7979.

Основные графики

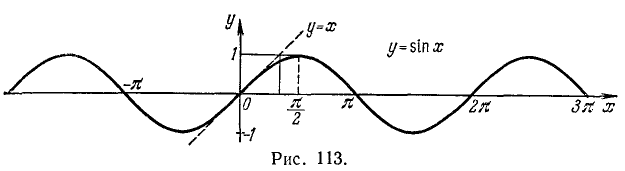
1 . Синусоида (график функции у = sin x).

1) Область определения (существования) функции:

х — любое действительное число (— < х < +).

2) Область изменения функции:

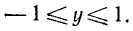
3) Периодичность функции:

sin x — периодическая функция с основным периодом, равным .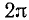

4) Четность функции:

sin х — нечетная функция, ибо sin (—х) =— sin x.

На основании пп. 3) и 4) достаточно построить график функции y= sin х на отрезке 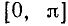, а затем продолжить его нечетно на отрезок 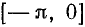и, наконец, то, что получится на отрезке 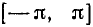, продолжить периодически на всю числовую ось. Итак, в дальнейшем будем изучать поведение нашей функции на отрезке .

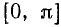5) Точки пересечения с осями координат:

а) с осью Оу (х = 0): у (0) = sin 0 = 0; график функции у = sin х проходит через начало координат;

6) с осью Ох (у = 0) (нули функции).

Найдем те х, при которых y = sin x = 0. Такими значениями будут числа 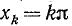(k = 0, ± 1, ±2, …). Нас интересуют 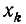из отрезка 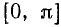. Такими 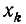будут 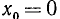(уже найдено) и 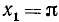, а остальные нули функции расположены вне отрезка 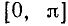. Следовательно, нули sin x на отрезке 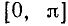совпадают с концами этого отрезка.

б) Наименьшие и наибольшие значения функции на отрезке .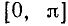

Функция у = sin x на отрезке 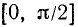монотонно возрастает от 0 до +1, а на отрезке 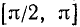монотонно убывает от +1 до 0 (см. п. 98). Следовательно, наименьшими значениями будут y (0) = sin 0 = 0 и 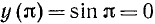; наибольшее значение достигается в одной точке: .

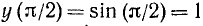7) Интервалы знакопостоянства функции.

На исследуемом отрезке 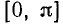наша функция всюду неотрицательна, т. е. .

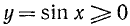8) На основании неравенств 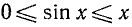для 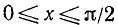(п. 109) мы заключаем, что наша синусоида на отрезке 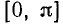должна располагаться ниже биссектрисы y = х первого координатного угла. Так как при этом 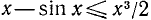, т. е. является при малых х весьма малой величиной, то график у = sin x близок к графику у = х (касается биссектрисы I координатного угла).

После того как функция исследована, приступаем к построению ее графика. Для этого найдем некоторые «опорные» точки его, а затем соединим их плавной линией с учетом свойств функции sin x. Для построения некоторых «опорных» точек можно, например, применить два способа.

Первый способ. Составим таблицу значений для sin x на отрезке 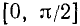с шагом h = 0,2 с точностью до 0,01. (Длина последнего отрезка 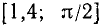на оси Ох немного меньше 0,2).

Значения для синуса взяты из таблицы тригонометрических функций (приложение II).

Второй способ. Воспользуемся геометрическими соображениями. Рассмотрим первую четверть единичной окружности (рис. 112). Разделим ее и соответствующий ей отрезок 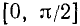оси Ох, например, на 8 равных частей.

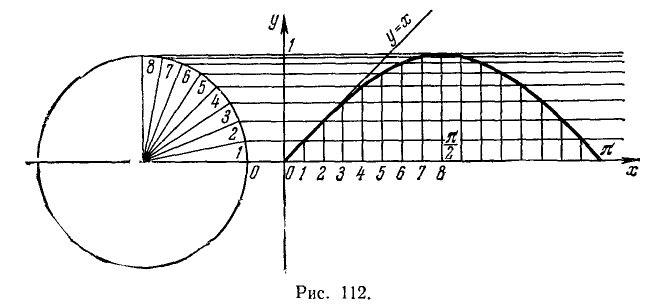
Величина перпендикуляра, опущенного из точки деления окружности на ось Ох, численно равна значению синуса соответствующего угла и значению синуса соответствующего числового аргумента из отрезка 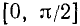оси Ох. Во второй четверти 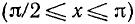синус убывает от 1 до 0. На основании нашего геометрического построения можно заключить, что график синуса во второй четверти 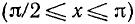симметричен его графику в первой четверти относительно прямой .

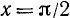Соединив полученные вторым (или первым) способом «опорные» точки плавной линией, мы получим график синуса (синусоиду) на отрезке 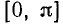. При проведении линии (построении графика) следует иметь в виду свойства 2), 6), 7) и 8). Затем продолжим график синуса на отрезок 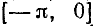, используя нечетность синуса, а именно построим на отрезке 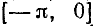график, симметричный графику синуса на отрезке 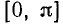относительно начала координат. Имея график синуса, построенный на отрезке 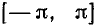, мы, используя его периодичность, сможем продолжить его на всю числовую ось (рис. 113).

2. График функции у = cos х. На основании формулы приведения мы имеем .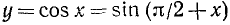

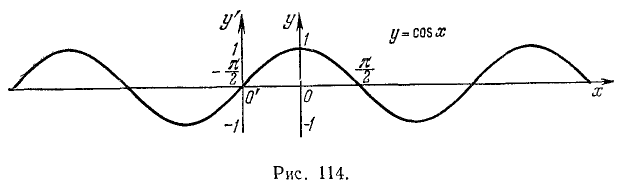
Следовательно, график косинуса — это синусоида, сдвинутая по оси Ох влево на 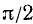. График косинуса построен на рис. 114.

3. Тангенсоида (график функции у= tg x). 1) Область определения функции:

х — любое действительное число, кроме чисел вида 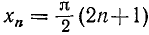, где n = 0, ±1, ±2… .

2) Область изменения функции:

— < у < +.

3) Периодичность функции:

tg x — периодическая функция с основным периодом, равным .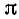

4) Четность функции:

tg x — нечетная функция, ибо tg (—х) = — tg x.

На основании 3) и 4) достаточно построить график функции у = tg х на отрезке 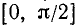, а далее продолжить его нечетно на отрезок 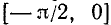и, наконец, то, что получится на отрезке 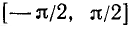, продолжить периодически на всю числовую ось. Итак, в дальнейшем будем изучать поведение нашей функций на отрезке .

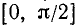5) Точки пересечения с осями координат:

а) с осью Оу (х = 0): y (0)= tg 0 = 0; график функции y = tg x проходит через начало координат;

б) с осью Ох (у = 0) (нули функции).

Найдем те значения х, при которых tg x = 0. Такими значениями будут 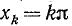(k = 0, ±1, ±2, …). Нас интересуют 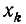из отрезка 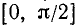: 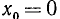(уже найдено), а остальные нули функции расположены вне отрезка 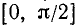. Следовательно, единственный нуль tg x, находящийся на отрезке 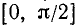, совпадает с левым концом этого отрезка.

6) Вертикальные асимптоты:

tg x определен всюду на отрезке 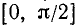, кроме точки .

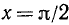Так как при 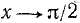, , 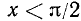то прямая 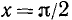является вертикальной асимптотой для графика функции у = tg x.

7) Наименьшие и наибольшие значения функции на отрезке .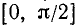

На основании п. 98 функция tg x на отрезке 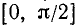монотонно возрастает от 0 до +. Следовательно, наименьшее значение будет y (0) = tg 0 = 0, а наибольшего значения не будет, ибо 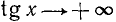, когда , .

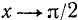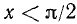8) Интервалы знакопостоянства функции.

На исследуемом отрезке 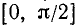функция tg x всюду неотрицательна, т. е. 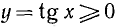. Следовательно, график функции лежит над осью Ох. На основании неравенств 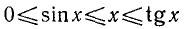(см. (109.1)) для 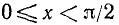мы заключаем, что тангенсоида на отрезке 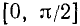должна располагаться выше биссектрисы у = х первого координатного угла.

После того как функция исследована, приступаем к построению ее графика. Для этого найдем некоторые «опорные» точки его, а затем соединим их плавной линией с учетом свойств функции tg x. Для построения «опорных» точек можно применять один из двух уже знакомых нам способов.

Первый способ. Составим таблицу значений для tg x на отрезке 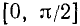с шагом h = 0,2 и с точностью до 0,01. (Длина последнего отрезка 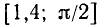на оси Ох немного меньше 0,2).

Значения для тангенса взяты из таблицы тригонометрических функций (приложение II).

Второй способ. Воспользуемся геометрическими соображениями аналогично тому, как мы это делали в случае построения графика функции y = sin x. Разделим опять первую четверть единичной окружности и соответствующий ей отрезок 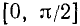оси Ох, например, на 8 равных частей. На оси тангенсов получим отрезки, численно равные тангенсам соответствующих углов.

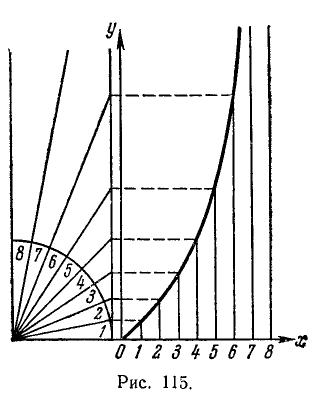
Далее, эти отрезки перенесем в соответствующие точки оси Ох. Концы их соединим плавной линией и получим график функции у = tgx (рис. 115). Вся тангенсоида изображена на рис. 116.

4. График функции у = ctg x изображен на рис. 117. Рекомендуем читателю самостоятельно построить его двумя способами:

1) составить таблицу значений для ctg x на отрезке 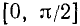с шагом h = 0,2 и точностью до 0,01;

2) воспользоваться формулой приведения .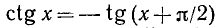

Указания к способу 1). При составлении таблицы значений для clg x воспользоваться формулой ctg x = 1/tg x и таблицей тригонометрических функций (приложение II), например: ctg 1,0 = 1/tg 1,0= 1/1,557 = 0,64.

Указания к способу 2). 1) Построить график функции у= tg x;

2) сдвинуть построенный график влево по оси Ох на 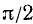(получим график функции );

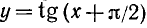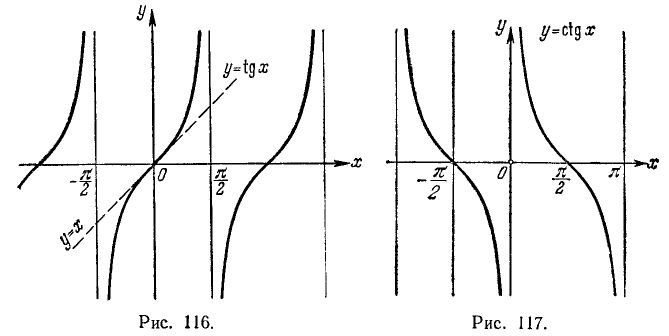
3) последний график зеркально отразить (перевернуть) относительно оси Ох (после выполнения последнего действия получим график функции y = ctg x).

Примеры построения графиков некоторых других тригонометрических функций

В дальнейшем мы будем коротко говорить: построить график функции y = f (x), а понимать под этим следующее: провести исследование функции y = f (x) и построить ее график. Рассмотрим некоторые примеры.

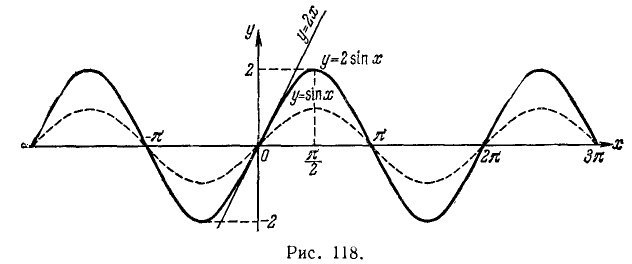
Пример:

Построить график функции у = 2sin x.

Решение:

Заметим, что график функции у = 2sin x получается из графика функции у = sin x, исследование которой проведено в начале п. 111, умножением каждой его ординаты на 2. Нули же функции sin x совпадают с нулями функции 2sin x. График функции у = 2sin x изображен на рис. 118.

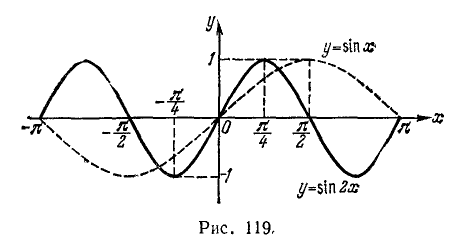
Пример:

Построить график функции y = sin2x.

Решение:

Заметим, что график функции y = sin2x получается из графика функции у = sin x сжатием по оси Ох в два раза (см. п. 47). Основным периодом для функции у = sin2x будет уже число . График функции y = sin2x изображен на рис. 119.

Пример:

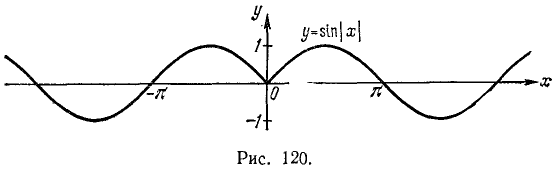
Построить графики функций: a) y = sin |x|; б) y = |sin x|.

Решение:

а) Воспользуемся общим правилом (п. 48) построения графика функции y = f (|х|) по графику функции у = f (х): сохраняем часть графика 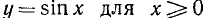и зеркально отражаем ее относительно оси Оу (часть графика у = sin x для х < 0 просто отбрасываем). Получаем график, показанный на рис. 120.

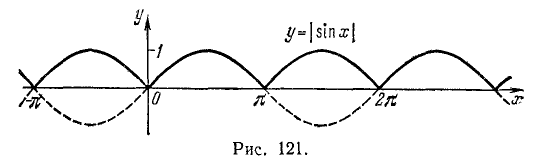
б) Снова используем результаты п. 48. Сохраняем часть синусоиды у = sin x, расположенную выше оси Ох; часть синусоиды, лежащая ниже оси Ох, зеркально отражается в оси Ох. Получаем график функции y = |sin x|, показанный на рис. 121.

Дальнейшие примеры построения графиков функций

Пример:

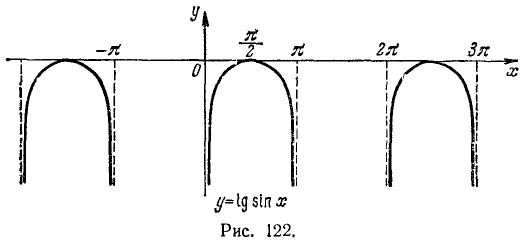
Построить график функции y= lg sin x.

Решение:

1) Область определения функции.

Функция определена для тех значений аргумента х, для которых sin x > 0. Такие значения аргумента заключены в пределах 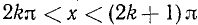, где k = 0, ±1, ±2, …

2) Периодичность функции.

sin x — периодическая функция с основным периодом, равным 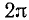. Следовательно, для тех х, для которых определена функция y = lg sin x, мы будем иметь 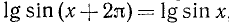, т. е. исследуемая функция будет иметь периодом также число 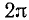. Исходя из соображений периодичности, достаточно исследовать нашу функцию на любом отрезке длины 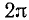, например на отрезке 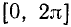. Но на отрезке 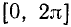наша функция определена не всюду —она определена только в интервале 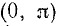, поэтому в дальнейшем будем изучать поведение данной функции в интервале .

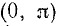3) Область изменения функции.

В интервале 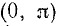наибольшее значение, которое принимает sin x, равно 1 (в точке 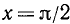), а наименьшего значения нет, но пр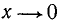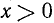и , , и 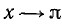, , 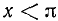, 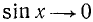оставаясь положительным. Функция lg sin x сначала возрастает от 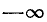до 0 (при 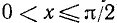), а затем убывает от 0 до 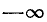(при 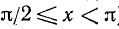). Итак, .

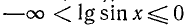4) Четность функции.

Функция y = lg sin x ни четная, ни нечетная.

5) Точки пересечения с осями координат:

а) с осью Оу (х = 0); наша функция определена только в интервале 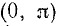, а в точке х = 0 она не существует, поэтому точки пересечения с осью Оу не существует;

б) с осью Ох (у = 0) (нули функции); наша функция обращается в нуль в единственной точке интервала 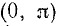— в точке 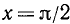, а в остальных точках этого интервала она отлична от нуля.

6) Вертикальные асимптоты.

Заметим, что прямые х = 0 и 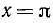являются вертикальными асимптотами для нашей функции, ибо 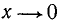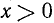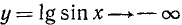при , , и при , , .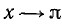

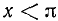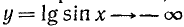7) Интервалы знакопостоянства функции.

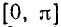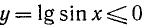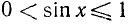На исследуемом отрезке наша функция всюду неположительна, т. е. , ибо . Следовательно, график функции лежит под осью Ох.

8) Наименьшие и наибольшие значения функции на отрезке .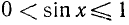

Наибольшего значения функция достигает в единственной точке 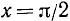, и это значение равно 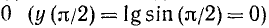. Наименьшего значения функция не имеет, ибо при 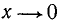, , 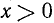и при 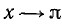, , 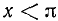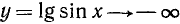. График функции y = lg sin x изображен на рис. 122.

Пример:

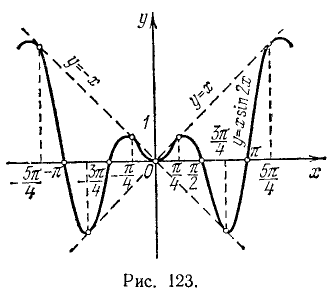
Построить график функции y = x sin 2x.

Решение:

1) Область определения функции: х — любое действительное число.

2) Область расположения графика функции.

Заметим, что 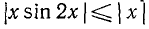(так как 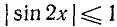, поэтому

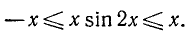
Геометрически это означает, что график функции у = х sin 2х заключен между графиками функций у = —х и у = х.

3) Четность функции.

Данная функция, как произведение двух нечетных функций (х и sin2x), есть функция четная.

В дальнейшем будем исследовать функцию при .

4) Точки пересечения с осями координат:

а) с осью Оу (х = 0); при х = 0 мы имеем у = 0, следовательно, график функции проходит через начало координат;

б) с осью Ох (у = 0) (нули функции); функция обращается в нуль в точках, где sin 2x = 0, т. е. в точках вида 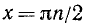(n = 0, 1, 2, …).

5) Точки, в которых функция принимает значения, равные х, или —х.

a) x sin 2x = x в точках, где sin 2x = 1, т. е. в точках

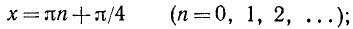
б) x sin 2x = — х в точках, где sin 2x =—1, т. е. в точках

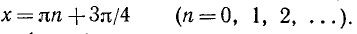
Построим график функции сначала для , а затем, используя четность нашей функции, отразим его зеркально в оси Оу. График функции у = — х sin 2х изображен на рис. 123.

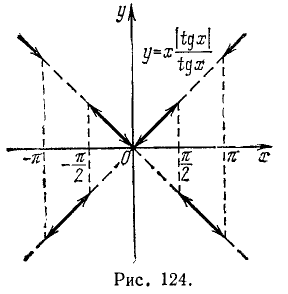
Пример:

Построить график функции .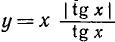

Решение:

1) Область определения функции.

Функция определена для тех значений х, для которых существует и отлична от нуля функция tg x, т. е. для всех х, кроме 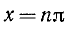и 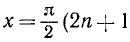, где n = 0, ±1, ±2, … .

2) Для всех х из области определения функции имеем

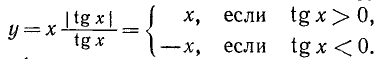
3) Четность функции. Функция — четная. Следовательно, достаточно сначала построить ее график для х > 0.

4) Заметим, что tg х > 0 при х > 0 в интервалах

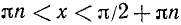, где n = 0,1,2,…,

т. е. в интервалах 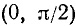, 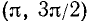и т.д.; tg x < 0 при х > 0 в интервалах

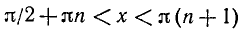, где n = 0,1,2,…,

т. е. в интервалах 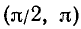, 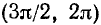и т. д.

Окончательно имеем (для x > 0)

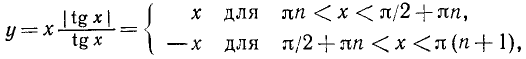
Построим график функции сначала для х > 0, а затем, используя четность данной функции, отразим его зеркально в оси Оу.

График функции 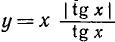изображен на рис. 124.

Решение заданий и задач по предметам:

• Математика
• Высшая математика
• Математический анализ
• Линейная алгебра

Дополнительные лекции по высшей математике:

1. Тождественные преобразования алгебраических выражений
2. Функции и графики
3. Преобразования графиков функций
4. Квадратная функция и её графики
5. Алгебраические неравенства
6. Неравенства
7. Неравенства с переменными
8. Прогрессии в математике
9. Арифметическая прогрессия
10. Геометрическая прогрессия
11. Показатели в математике
12. Логарифмы в математике
13. Исследование уравнений
14. Уравнения высших степеней
15. Уравнения высших степеней с одним неизвестным
16. Комплексные числа
17. Непрерывная дробь (цепная дробь)
18. Алгебраические уравнения
19. Неопределенные уравнения
20. Соединения
21. Бином Ньютона
22. Число е
23. Непрерывные дроби
24. Функция
25. Исследование функций
26. Предел
27. Интеграл
28. Двойной интеграл
29. Тройной интеграл
30. Интегрирование
31. Неопределённый интеграл
32. Определенный интеграл
33. Криволинейные интегралы
34. Поверхностные интегралы
35. Несобственные интегралы
36. Кратные интегралы
37. Интегралы, зависящие от параметра
38. Квадратный трехчлен
39. Производная
40. Применение производной к исследованию функций
41. Приложения производной
42. Дифференциал функции
43. Дифференцирование в математике
44. Формулы и правила дифференцирования
45. Дифференциальное исчисление
46. Дифференциальные уравнения
47. Дифференциальные уравнения первого порядка
48. Дифференциальные уравнения высших порядков
49. Дифференциальные уравнения в частных производных
50. Тригонометрические функции
51. Тригонометрические уравнения и неравенства
52. Показательная функция
53. Показательные уравнения
54. Обобщенная степень
55. Взаимно обратные функции
56. Логарифмическая функция
57. Уравнения и неравенства
58. Положительные и отрицательные числа
59. Алгебраические выражения
60. Иррациональные алгебраические выражения
61. Преобразование алгебраических выражений
62. Преобразование дробных алгебраических выражений
63. Разложение многочленов на множители
64. Многочлены от одного переменного
65. Алгебраические дроби
66. Пропорции
67. Уравнения
68. Системы уравнений
69. Системы уравнений высших степеней
70. Системы алгебраических уравнений
71. Системы линейных уравнений
72. Системы дифференциальных уравнений
73. Арифметический квадратный корень
74. Квадратные и кубические корни
75. Извлечение квадратного корня
76. Рациональные числа
77. Иррациональные числа
78. Арифметический корень
79. Квадратные уравнения
80. Иррациональные уравнения
81. Последовательность
82. Ряды сходящиеся и расходящиеся
83. Тригонометрические функции произвольного угла
84. Тригонометрические формулы
85. Обратные тригонометрические функции
86. Теорема Безу
87. Математическая индукция
88. Показатель степени
89. Показательные функции и логарифмы
90. Множество
91. Множество действительных чисел
92. Числовые множества
93. Преобразование рациональных выражений
94. Преобразование иррациональных выражений
95. Геометрия
96. Действительные числа
97. Степени и корни
98. Степень с рациональным показателем
99. Тригонометрические функции угла
100. Тригонометрические выражения и их преобразования
101. Преобразование тригонометрических выражений
102. Комбинаторика
103. Вычислительная математика
104. Прямая линия на плоскости и ее уравнения
105. Прямая и плоскость
106. Линии и уравнения
107. Прямая линия
108. Уравнения прямой и плоскости в пространстве
109. Кривые второго порядка
110. Кривые и поверхности второго порядка
111. Числовые ряды
112. Степенные ряды
113. Ряды Фурье
114. Преобразование Фурье
115. Функциональные ряды
116. Функции многих переменных
117. Метод координат
118. Гармонический анализ
119. Вещественные числа
120. Предел последовательности
121. Аналитическая геометрия
122. Аналитическая геометрия на плоскости
123. Аналитическая геометрия в пространстве
124. Функции одной переменной
125. Высшая алгебра
126. Векторная алгебра
127. Векторный анализ
128. Векторы
129. Скалярное произведение векторов
130. Векторное произведение векторов
131. Смешанное произведение векторов
132. Операции над векторами
133. Непрерывность функций
134. Предел и непрерывность функций нескольких переменных
135. Предел и непрерывность функции одной переменной
136. Производные и дифференциалы функции одной переменной
137. Частные производные и дифференцируемость функций нескольких переменных
138. Дифференциальное исчисление функции одной переменной
139. Матрицы
140. Линейные и евклидовы пространства
141. Линейные отображения
142. Дифференциальные теоремы о среднем
143. Теория устойчивости дифференциальных уравнений
144. Функции комплексного переменного
145. Преобразование Лапласа
146. Теории поля
147. Операционное исчисление
148. Системы координат
149. Рациональная функция
150. Интегральное исчисление
151. Интегральное исчисление функций одной переменной
152. Дифференциальное исчисление функций нескольких переменных
153. Отношение в математике
154. Математическая логика
155. Графы в математике
156. Линейные пространства
157. Первообразная и неопределенный интеграл
158. Линейная функция
159. Выпуклые множества точек
160. Система координат