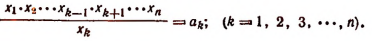Оглавление:
Уравнения высших степеней с одним неизвестным:
Биквадратное уравнение
Как известно, целое уравнение, содержащее только четвертую, вторую и нулевую степени неизвестного, называется биквадратным.
Уравнение
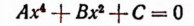
представляет собой общий вид биквадратного уравнения. Принимая за новое неизвестное 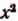 , получим:
, получим:
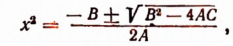
откуда
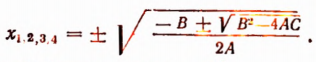
Свойства корней биквадратного уравнения.
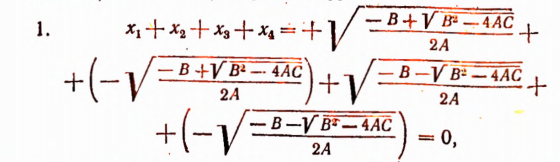
т. е. сумма корней биквадратного уравнения равна нулю как и надо было ожидать согласно теореме Виета, так как коэффициент при 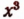 в биквадратном уравнении равен нулю.
в биквадратном уравнении равен нулю.
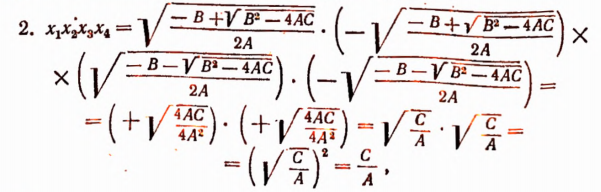
т. е. произведение корней биквадратного уравнения равно отношению свободного члена к коэффициенту при четвертой степени неизвестного.
Возвратное уравнение 4-й степени
Общий вид возвратного уравнения 4-й степени таков:
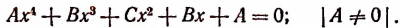
Нуль не является корнем этого уравнения, поэтому можно разделить все члены уравнения на 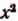 и привести уравнение к виду:
и привести уравнение к виду:
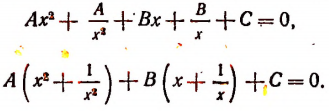
Введем новое неизвестное 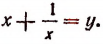
Тогда
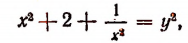
откуда
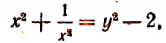
что приведет нас к квадратному уравнению 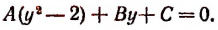
Найдя 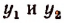 и пользуясь уравнением
и пользуясь уравнением
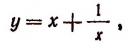
найдем 4 значения неизвестного х.
Двучленные уравнения
1. Двучленное уравнение 3-й степени 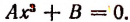
а) Пусть из двух чисел А и В одно положительное, а другое отрицательное. Положим, что
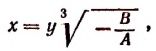
где под выражением  будем подразумевать лишь его арифметическое значение. (Как известно, арифметическое значение корня легко вычисляется с помощью таблиц логарифмов.)
будем подразумевать лишь его арифметическое значение. (Как известно, арифметическое значение корня легко вычисляется с помощью таблиц логарифмов.)
Подставляя в данное уравнение вместо х выражение 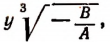 получим:
получим:
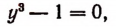
или
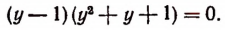
Отсюда
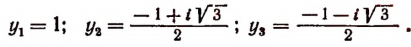
Пользуясь формулой
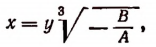
найдем все три корня исходного уравнения:
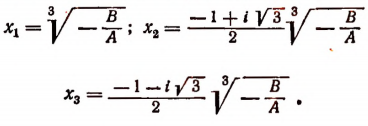
б) Пусть А и В одновременно положительны или одновременно отрицательны. Положим, что
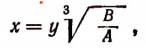
где под выражением 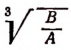 будем подразумевать опять лишь его арифметическое значение.
будем подразумевать опять лишь его арифметическое значение.
Из исходного уравнения получим:
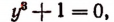
или

Отсюда
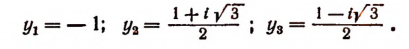
Пользуясь формулой
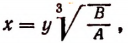
найдем все три корня исходного уравнения:
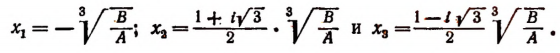
2. Двучленное уравнение 4-й степени 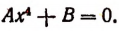
а) Пусть из двух чисел А и В одно положительное, а другое отрицательное. Положим, что
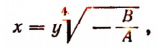
где под выражением
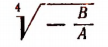
будем подразумевать лишь его арифметическое значение. Тогда из исходного уравнения получим:
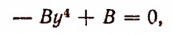
или
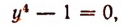
т. е. получим опять двучленное уравнение 4-й степени, но уже в его простейшей форме.
Решив уравнение 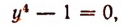 найдем его четыре корня:
найдем его четыре корня:
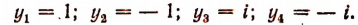
Пользуясь уравнением
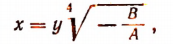
найдем все 4 корня исходного уравнения:
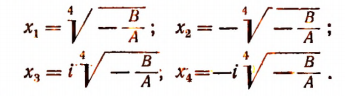
б) Пусть оба числа А и В одновременно положительны либо одновременно отрицательны. Положим, что
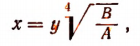
где под выражением 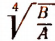 будем опять подразумевать лишь его арифметическое значение. Тогда из исходного уравнения получим:
будем опять подразумевать лишь его арифметическое значение. Тогда из исходного уравнения получим:
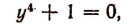
т. е. опять двучленное уравнение, но уже в его простейшей форме.
Разложим левую часть последнего уравнения на множители:
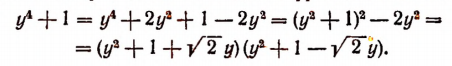
Теперь легко обнаружить, что корнями уравнения
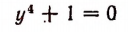
будут
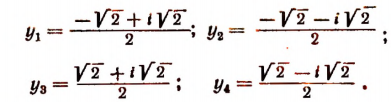
Пользуясь уравнением
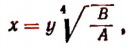
найдем:
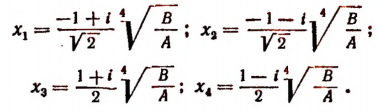
3.Двучленное уравнение 6-й степени 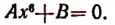
а) Пусть из двух чисел А и В одно положительное, а другое отрицательное. Положим, что
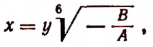
где под выражением
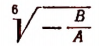
будем, как и выше, подразумевать лишь его арифметическое значение. Тогда из исходного уравнения получим:
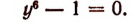
Разложив левую часть этого уравнения на множители, получим:
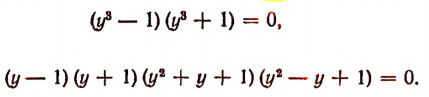
Найдя 6 корней этого уравнения, определим и 6 корней исходного уравнения так же, как это мы делали в предыдущих случаях.
б) Пусть оба числа А и В либо одновременно положительны, либо одновременно отрицательны. Положим, что
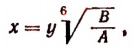
тогда получим:
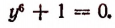
Разложив левую часть этого уравнения на множители, получим:
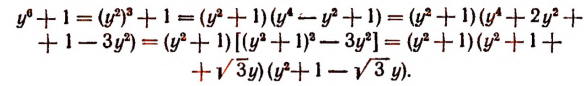
Таким образом, решение уравнения + 1 = О сводится к решению уравнения
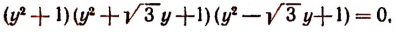
Отсюда
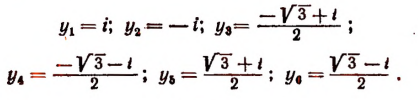
Пользуясь формулой 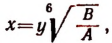 найдем шесть корней уравнения
найдем шесть корней уравнения
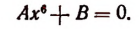
Второй способ решения двучленного уравнения
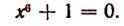
Положим, что x=iy. Тогда задача сведется к решению уравнения
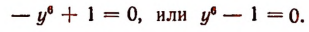
Найдя все 6 корней последнего уравнения и пользуясь равенством х=iy, найдем все 6 корней уравнения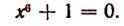
4. Двучленное уравнение п-й степени 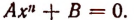
а) Пусть из двух чисел А и В одно положительное и другое отрицательное. Положим, что
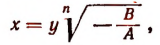
где под выражением 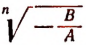 будем, как и раньше, подразумевать лишь его арифметическое значение. Тогда из исходного уравнения получим:
будем, как и раньше, подразумевать лишь его арифметическое значение. Тогда из исходного уравнения получим:
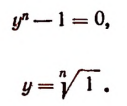
Найдя все п значений 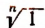 (см. стр. 590), получим п значений неизвестного у, а затем и все п корней исходного уравнения.
(см. стр. 590), получим п значений неизвестного у, а затем и все п корней исходного уравнения.
б) Пусть числа АнВ одновременно положительны или одновременно отрицательны. Положим, что
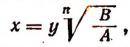
где под выражением  будем опять-таки подразумевать лишь его арифметическое значение. Тогда получим:
будем опять-таки подразумевать лишь его арифметическое значение. Тогда получим:
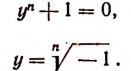
Найдя все п значений  , получим п значений неизвестного у, а затем и все п корней исходного уравнения:
, получим п значений неизвестного у, а затем и все п корней исходного уравнения:
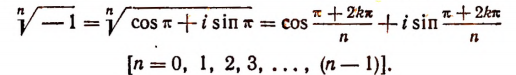
Заметим, что двучленное уравнение
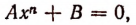
где 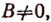 никогда не имеет кратных корней. Уравнение
никогда не имеет кратных корней. Уравнение
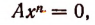
где 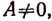 имеет один п-кратный корень, равный нулю.
имеет один п-кратный корень, равный нулю.
Другими словами, все п корней этого уравнения одинаковы и каждый равен нулю, т.е.
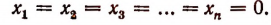
Трехчленные уравнения
Общий вид трехчленного уравнения таков:
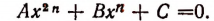
Решение трехчленного уравнения подстановкой 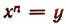 сводится к квадратному уравнению
сводится к квадратному уравнению
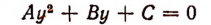
и далее к двучленному уравнению п-й степени.
Пример:
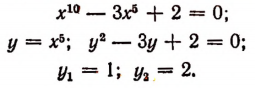
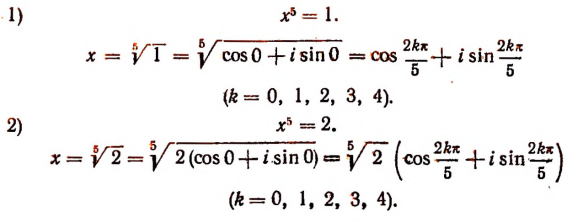
Целое алгебраическое уравнение
Уравнение, в котором правая часть есть нуль, а левая — целая рациональная функция п-й степени, т. е.
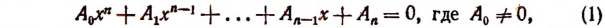
называется целым алгебраическим уравнением п-й степени с одним неизвестным.
При п = 1 и п = 2 (как известно) это уравнение решается легко.
Вопрос о решении этого уравнения в общем виде при п = 3 и п = 4 освещен в конце настоящей главы. Вопрос же о решении уравнения (I) в общем виде при п > 4 изучается в специальных курсах современной алгебры. Корни уравнений степени выше 4-й не выражаются через коэффициенты уравнения посредством элементарных функций.
Наряду с этим обратная задача, т. е. задача составления уравнения п-й степени по данным его корням, решается легко.
В самом деле, пусть нам даны корни 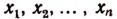 уравнения п-й степени. Тогда само уравнение может быть записано в виде
уравнения п-й степени. Тогда само уравнение может быть записано в виде
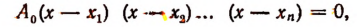
где 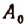 — произвольное число, не равное нулю.
— произвольное число, не равное нулю.
Раскрыв скобки и сгруппировав члены, содержащие одинаковые степени неизвестного, получим искомое уравнение в виде

где коэффициенты 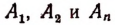 вполне определятся в зависимости от
вполне определятся в зависимости от 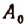 и от чисел
и от чисел 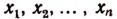 .
.
Пример:
Составить уравнение 5-й степени по данным его корням:
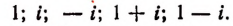
Искомым уравнением будет:
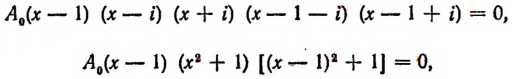
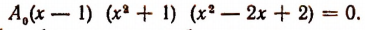
Положив  и раскрыв скобки, получим искомое уравнение в виде
и раскрыв скобки, получим искомое уравнение в виде
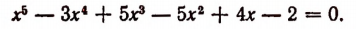
Отыскание рациональных корней целого алгебраического уравнения с целыми коэффициентами
Приведенное уравнение
Пусть в приведенном уравнении
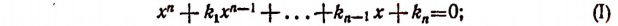
все коэффициенты 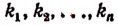 — целые числа и
— целые числа и 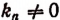 . Докажем следующие две теоремы.
. Докажем следующие две теоремы.
Теорема:
Если уравнение (I) имеет целый корень, то он обязательно будет делителем свободного члена 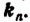
Доказательство:
Допустим, что целое число l, не равное нулю, есть корень уравнения (I). Тогда получим:
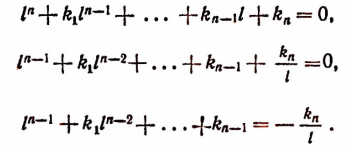
В левой части уравнения мы имеем целое число. Следовательно, l должно быть делителем свободного члена 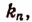 что и требовалось доказать.
что и требовалось доказать.
Следствие:
Если ни один из делителей свободного члена не является корнем уравнения (I), то последнее не имеет ни одного целого корня.
Теорема:
Уравнение (I) не может иметь ни одного дробного корня.
Доказательство:
Применим метод доказательства от противного. Допустим, что уравнение (I) имеет дробный корень 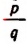 , где р и q — целые взаимно простые числа. Тогда получим:
, где р и q — целые взаимно простые числа. Тогда получим:
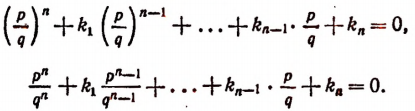
Умножив на 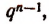 получим:
получим:
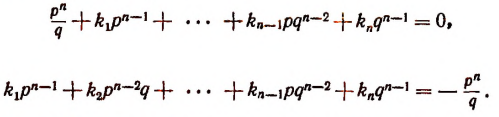
Но последнее равенство невозможно, так как его левая часть есть число целое, а правая — дробное.
Следовательно, уравнение (I) не может иметь ни одного дробного корня.
Итак, уравнение (I) может иметь корни либо целые, либо иррациональные, либо мнимые.
Для нахождения целых корней уравнения (I) надо производить испытание делителей свободного члена. Если ни один делитель свободного члена не окажется корнем уравнения (I), то это будет означать (как это уже было доказано выше), что оно не имеет нн одного целого корня. В этом случае корнями уравнения (I) могут быть либо иррациональные, либо мнимые числа.
Примеры:
1. Найти целые корни уравнения:
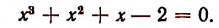
Делителями свободного члена являются лишь числа 1; —1; 2; — 2. Ни один нз этих делителей не является корнем данного уравнения. Следовательно, оно не имеет нн одного целого корня.
2. Найти целые корни уравнения:

Делители 1;— 1; 2 не являются корнями этого уравнения. Делитель же — 2 является корнем данного уравнения. Следовательно, данное уравнение имеет только один целый корень, равный — 2.
Разделив многочлен  на х + 2, получим в частном
на х + 2, получим в частном  . Поэтому данное уравнение может быть записано в виде
. Поэтому данное уравнение может быть записано в виде
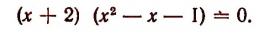
Отсюда получим и остальные два корня данного уравнения:
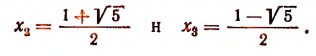
Неприведенное уравнение
Пусть в неприведенном уравнении
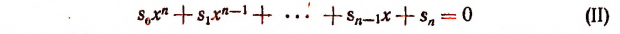
все коэффициенты 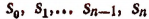 — целые числа и
— целые числа и 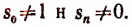
Поставим следующую задачу. Найти все рациональные корни уравнения (II).
Умножив обе части уравнения на 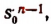 получим:
получим:
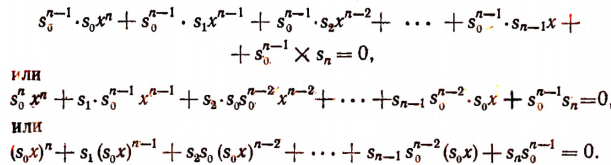
Примем за новое неизвестное произведение 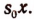 Полагая
Полагая 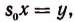 получим:
получим:
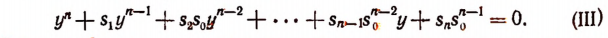
Таким обратом, мы пришли к уравнению относительно у, которое также имеет целые коэффициенты, но которое уже является приведенным. Это уравнение, как уже известно, дробных корней иметь не может. Но у него могут быть или не быть целые корни.
Если окажется, что уравнение (III) имеет целые корни, то каждому его.целому корню 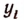 будет соответствовать (в силу равенства
будет соответствовать (в силу равенства 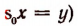 рациональный корень
рациональный корень 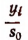 уравнения (II).
уравнения (II).
Если окажется, что уравнение (III) не имеет ни одного целого корня, то это будет означать, что уравнение (II) не имеет ни одного рационального корня.
Примеры:
1.Найти рациональные корни уравнения
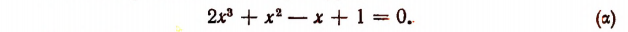
Умножив на 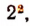 получим:
получим:
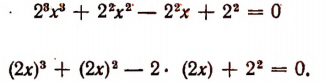
Полагая 2х = у, получим:
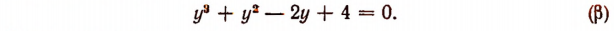
Делители свободного члена:

Ни один из этих делителей не является корнем уравнения 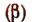 , т. е. уравнение
, т. е. уравнение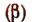 не имеет ни одного целого корня. Следовательно, первоначальное уравнение (а) на имеет ни одного рационального корня.
не имеет ни одного целого корня. Следовательно, первоначальное уравнение (а) на имеет ни одного рационального корня.
2. Найти рациональные корни уравнения
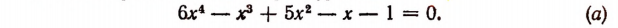
Умножив на 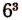 , получим:
, получим:
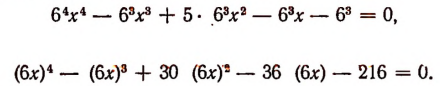
Полагая 6х = у, получим:
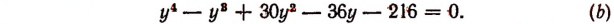
Испытывая делители числа 216, найдем, что числа — 2 и 3 являются корнями уравнения (b).
Найденным целым корням уравнения (b) будут соответствовать (в силу уравнения 6х = у) .дробные корни уравнения (а), а именно:
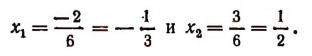
Зная два корня уравнения 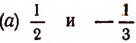 разделим его левую часть на произведение:
разделим его левую часть на произведение: 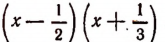 Для удобства деления предварительно умножим делимое и делитель на 6. Тогда получим:
Для удобства деления предварительно умножим делимое и делитель на 6. Тогда получим:
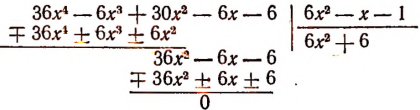
Остальные корни уравнения (а) будут решениями уравнения 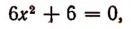
т. е. будут i и — i.
Итак, уравнение (а) имеет два рациональных корня 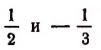 и два чисто мнимых корня i и —i.
и два чисто мнимых корня i и —i.
О решении уравнений 3-й и 4-й степени
Уравнение 3-й степени в общем виде таково:
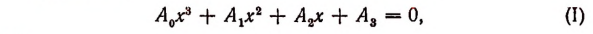
где
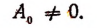
Решение этого уравнения всегда можно свести к решению уравнения
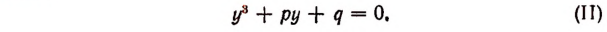
Действительно, разделив все члены уравнения (I) на 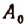 , получим уравнение в приведенной форме
, получим уравнение в приведенной форме
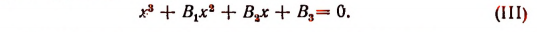
Применим к последнему уравнению преобразование
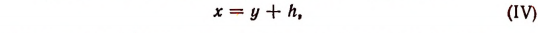
где у— новая неизвестная, а h— постоянная, значение которой мы в дальнейшем выберем так, как нам будет необходимо.
Подставив в уравнение (III) вместо х выражение у + h и расположив результат по степеням у, получим:
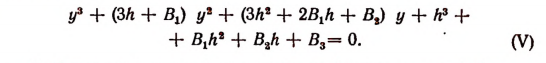
Выберем постоянную h так, чтобы коэффициент при 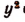 обратился в нуль, т. е. положим, что
обратился в нуль, т. е. положим, что
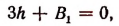
откуда
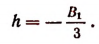
Подставляя это значение h в уравнение (V), получим:
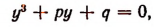
где
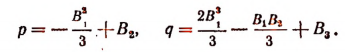
Теперь перейдем к решению уравнения
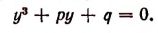
Неизвестное у представим в виде суммы двух новых неизвестных, т. е. положим, что
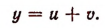
Тогда уравнение (Р) примет вид:
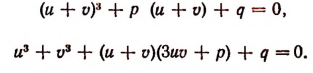
Так как мы вместо одного неизвестного у ввели два неизвестных u и v, то одно из них может быть выбрано произвольно; иначе говоря, мы можем установить между u и v еще одну произвольную зависимость.
Пользуясь этим, потребуем, чтобы 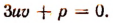 Тогда уравнение (Q) примет вид:
Тогда уравнение (Q) примет вид:
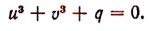
Таким образом, мы пришли к системе уравнений:
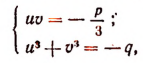
или
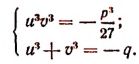
В этой системе за неизвестные примем 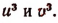 Тогда они определятся как корни квадратного уравнения
Тогда они определятся как корни квадратного уравнения
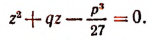
Таким образом, можем принять
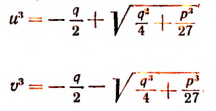
Определив отсюда u и v, найдем результат для неизвестного у:
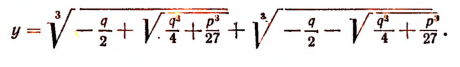
Получили так называемую формулу Кардаио для решения кубического уравнения.
Полные сведения о решении уравнения 3-й степени и о формуле Кардаио излагаются в учебниках по высшей алгебре.
Решение уравнения 4-й степени путем преобразований сводится к решению уравнения 3-й степени.
Некоторые системы уравнений высших степеней, решаемые искусственным путем
Примеры:
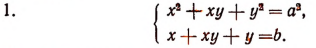
Преобразуем эту систему к виду:
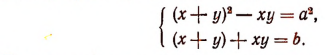
Полагая х+у = u и ху = v, получим:

Найдя решения этой системы, придем к двум отдельным системам вида:

Решения этой системы наиболее удобно находить с помощью квадратного уравнения:

(см. стр. 360).

Разложим левые части уравнений на множители:
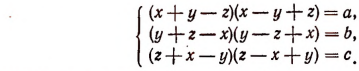
Перемножая и извлекая квадратный корень, получим:
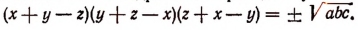
Сопоставляя это уравнение по очереди с каждым из предшествующих трех уравнений, получим:
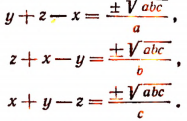
Складывая попарно, найдем два решения системы;
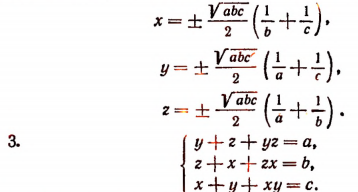
Прибавив к левой и правой частям каждого уравнения системы по единице, получим:
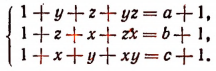
Разложим левые части системы на множители:
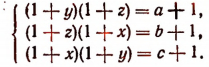
Перемножим левые и правые части уравнений системы и извлечем квадратный корень:
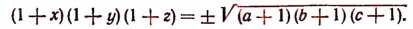
Пользуясь этим уравнением и каждым из трех предшествующих, получим:
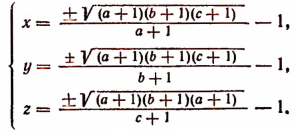
Система имеет два решения.
4. Найти положительные решения системы п уравнений с п неизвестными 
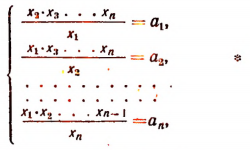
Эту систему можно было записать кратко так:
где все числа  — положительные.
— положительные.
Перемножив левые и правые части системы уравнений, получим:
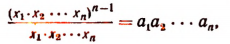
откуда
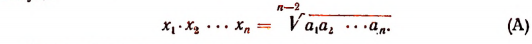
Из первого уравнения системы следует, что
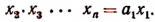
Пользуясь этим равенством и равенством (А), найдем, что
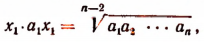
откуда
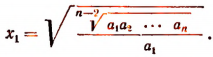
Аналогично находятся значения и остальных неизвестных.
Под появившимися корнями (п — 2)-й степени и 2-й степени мы подразумеваем здесь лишь их арифметические значения.
Данная система имеет лишь одно такое решение, при котором значения всех п неизвестных одновременно положительны. Это решение можно записать кратко так:
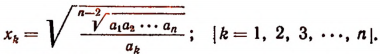
5. Решить систему:
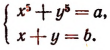
Преобразуем первое уравнение системы:
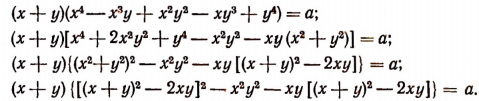
Так как х + у = b, то, заменив в последнем уравнении х + у через b и обозначив ху через z, получим квадратное уравнение
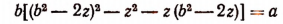
с одним неизвестным z. Решив это квадратное уравнение, найдем два значения для z, т е. для произведения ху.
Теперь задача сведется к решению двух отдельных систем вида:
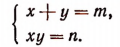
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат