Оглавление:
Квадратичная функция — целая рациональная функция второй степени вида 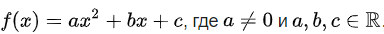 . Уравнение квадратичной функции содержит квадратный трёхчлен. Графиком квадратичной функции является парабола. Многие свойства графика квадратичной функции так или иначе связаны с вершиной параболы, которая во многом определяет положение и внешний вид графика.
. Уравнение квадратичной функции содержит квадратный трёхчлен. Графиком квадратичной функции является парабола. Многие свойства графика квадратичной функции так или иначе связаны с вершиной параболы, которая во многом определяет положение и внешний вид графика.
Формула корней квадратного уравнения
В первой части курса были выведены следующие формулы для определения корней неполного и полного квадратных уравнений:
1) αx²=0; очевидно, оба корня уравнения равны нулю.
2) αx²+с=0; формула для корней будет: 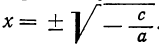
3) αx² +bx=0; тогда x₁ =0; х₂ =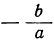
4) x² + +q=0; формула корней даёт: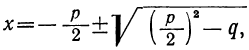 или:
или: 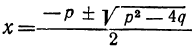 .
.
5) Наконец, общая формула для корней полного квадратного уравнения вида αx²+bx+c=0 будет: 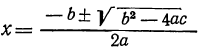
Последняя формула является наиболее общей; из неё как частные случаи получаются все остальные. Так, полагая в этой формуле α=l, получаем случай (4) (в этом случае b=p и c=q); полагая с=0, получаем случай (3); при b=0 будем иметь случай (2) и, наконец, первый случай получим, давая в общей формуле значения b=c=0.
Дискриминант
Рассмотрим различные случаи, которые могут встретиться при решении квадратного уравнения в зависимости от числового значения коэффициентов.
1. b² — 4αc>0. В этом случае выражение под корнем положительно. Квадратный корень из него имеет два значения, и, следовательно, уравнение имеет два различных вещественных корня: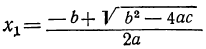 и
и 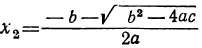 .
.
2. b² — 4αc=0. В этом случае второй член числителя равен нулю, и уравнение имеет два равных корня: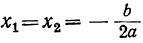
3. b² — 4αc<0. Оба корня — мнимые.
Мы видим, таким образом, что квадратное уравнение имеет вещественные (различные или равные) или мнимые корни, в зависимости от того, будет ли составленное из коэффициентов уравнения подкоренное выражение b² — 4αc больше, равно или меньше нуля. Ввиду особого значения этого выражения оно носит специальное название дискриминанта уравнения. (Дискриминант — значит в переводе р а з л и ч и т е л ь.)
Свойства корней квадратного уравнения (теорема Виета)
Возьмём формулу корней квадратного уравнения, у которого коэффициент при x² равен единице, т. е. уравнения вида x²+ +q=0: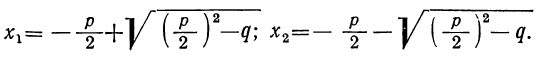
Если сложим почленно эти равенства, то радикалы взаимно уничтожатся, и мы получим: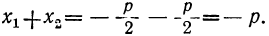
Если те же равенства почленно перемножим, то получим (произведение суммы двух чисел на их разность равно разности квадратов этих чисел):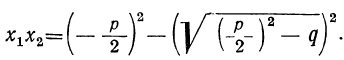
Каково бы ни было подкоренное число, всегда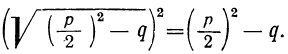
Следовательно: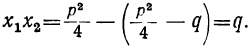
Таким образом:
Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение этих корней равно свободному члену.
Теперь возьмём квадратное уравнение общего вида αx²+bx+c=0. Разделив все его члены на а, мы приведём это уравнение к только что рассмотренному виду: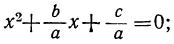
следовательно, для неприведённого полного уравнения мы должны иметь: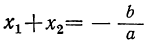 и
и 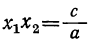 .
.
Следствия:
1) Пользуясь этими свойствами, мы легко можем составить квадратное уравнение, у которого корнями были бы данные числа.
Пусть, например, надо составить уравнение, у которого корни были бы числа 2 и 3. Тогда из равенства 2+3= — р и 2∙3 = q находим: р = — 5 и q=6; следовательно, уравнение будет: x²-5x+6=0.
Подобно этому найдём,что 3 и -7 будут корни уравнения x²- [3+(- 7)]x+3( -7) = 0, т. е. x²+4x-21=0; числа 3 и 0 будут корни уравнения x²— 3x=0.
2) При помощи тех же свойств мы можем, не решая квадратного уравнения, определить знаки его корней, если эти корни вещественные. Пусть, например, имеем уравнение x²+8x+12=0. Так как в этом примере выражение 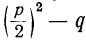 , т. е. 4² -12, есть число положительное, то оба корня вещественные. Обращая внимание на свободный член, видим, что он имеет знак +; значит, произведение корней должно быть положительное число, т. е. оба корня имеют одинаковые знаки. Эти знаки должны быть минусы, так как сумма корней отрицательна (она равна — 8). Уравнение x² +8x-12=0 имеет корни с разными знаками (потому что их произведение отрицательно), причём отрицательный корень имеет большую абсолютную величину (потому что их сумма отрицательна) и т. п.
, т. е. 4² -12, есть число положительное, то оба корня вещественные. Обращая внимание на свободный член, видим, что он имеет знак +; значит, произведение корней должно быть положительное число, т. е. оба корня имеют одинаковые знаки. Эти знаки должны быть минусы, так как сумма корней отрицательна (она равна — 8). Уравнение x² +8x-12=0 имеет корни с разными знаками (потому что их произведение отрицательно), причём отрицательный корень имеет большую абсолютную величину (потому что их сумма отрицательна) и т. п.
Трёхчлен второй степени
Выражение αx²+bx+c, в котором х означает независимое переменное, а α, b и с — какие-нибудь данные, постоянные числа, называется квадратной функцией, или трёхчленом второй степени. Различие между таким трёхчленом и левой частью уравнения αx²+bx+c=0 состоит в том, что в уравнении буква х означает только те числа, которые удовлетворяют уравнению, тогда как в трёхчлене она означает какое угодно число. Значения х, обращающие трёхчлен в нуль, называются его корнями; значит, корни трёхчлена-это корни квадратного уравнения:
αx² +6x+c=0.
В частном случае при α=1 трёхчлен принимает вид: x²+ +q; при b=0 или при с=0 трёхчлен обращается в двучлен αx²+c или αx²+bx.
Разложение трёхчлена второй степени
Сначала возьмём трёхчлен x²+ +q, в котором коэффициент при x² есть 1. Решив приведённое уравнение x²+ +q=0, мы найдём корни его х₁ и х₂ . Как мы сейчас видели: х₁+х₂ =-p и х₁х₂ =q.
Из этих равенств находим: р=- ( х₁+х₂) и q=х₁х₂
Подставим в трёхчлен на место р и q эти выражения и затем преобразуем полученный многочлен:
x²+ +q= x² — (х₁+ х₂)x+х₁х₂ = x²— х₁x — х₂x+ х₁х₂ =
= ( x²— х₁x) — (х₂x — х₁х₂) = х( x— х₁) — х₂ (x— х₁ ) = ( x— х₁)(x — х₂).
Таким образом:
Трёхчлен x² +q разлагается на два множителя, из которых первый равен разности между х и одним корнем трёхчлена, а второй равен разности между х и другим корнем трёхчлена.
Примеры: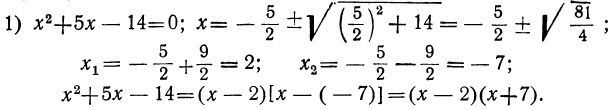
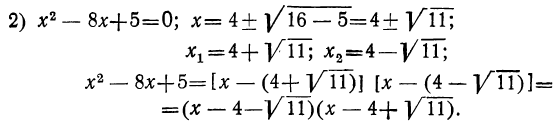
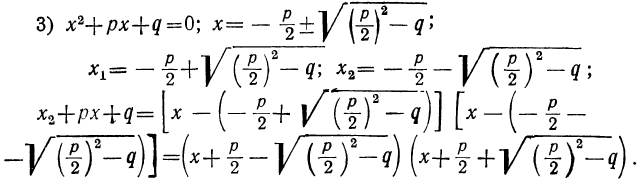
Теперь возьмём трёхчлен αx²+bx+c, в котором коэффициент при x² есть какое угодно число. Этот трёхчлен можно представить так: 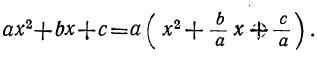
Выражение, стоящее внутри скобок, есть трёхчлен вида x²+ +q . Его корни х₁ и х₂ будут те же самые, что трёхчлена αx²+bx+c. Найдя их, мы можем, по доказанному, разложить этот трёхчлен так: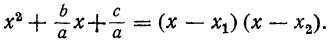
Следовательно: αx²+bx+c =α(x — х₁) (х — х₂).
Таким образом, разложение трёхчлена αx²+bx+c отличается от разложения трёхчлена x²+ +q только дополнительным множителем α.
Примеры:
1) Трёхчлен 2x² — 2х -12, корни которого 3 и — 2, можно разложить так: 2(x — 3)(x+2).
2) Трёхчлен 3x² + х +1, корни которого следующие: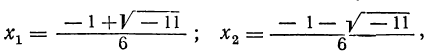
разлагается так: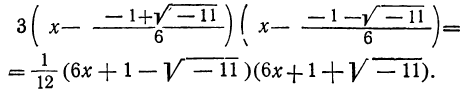
3) 6abx² — ( 3b³ +2α³)x+a²b² .
Корни этого трёхчлена следующие: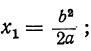
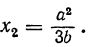
Поэтому: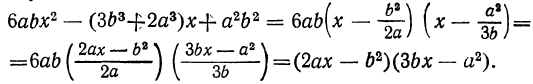
4) Сократить дробь: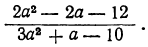
Разложим числитель и знаменатель на множители и затем, если можно, сократим дробь. Так как корни числителя 3 и —2, а корни знаменателя 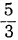 и — 2, то дробь представится так:
и — 2, то дробь представится так: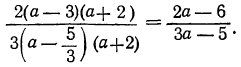
Следствие:
По данным корням можно составить квадратное уравнение. Так, уравнение, имеющее корни З и -2, будет:
(x-3)[x-( — 2)] =0, т. е. (х — 3)(x+2)=0,
что по раскрытии скобок даёт: x² — х — 6 = 0. Конечно, все члены этого уравнения можно умножить на произвольное число, не зависящее от х (например, на 2), отчего корни не изменятся.
Сократить следующие дроби (предварительно разложив числитель и знаменатель каждой дроби на множители):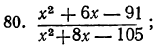
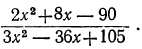
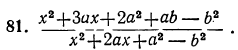
Разложив на множители следующие трёхчлены, определить, для каких значений х эти трёхчлены будут давать положительные числа и для каких — отрицательные: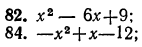
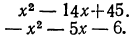
График квадратной функции
Графиком квадратичной функции является парабола.
График функции у=x²
Обратим внимание на следующие особенности функции y=x²;
а) При всяком значении аргумента х функция определена и получает только одно значение. Например, при x = — 10 значение функции будет (-10)² = 100, при x = 1000 значение функции будет 1000² = 1 000 000 и т. п.
б) Так как (—x)² =x² , то при двух значениях х, отличающихся только знаками, получаются два одинаковых положительных значения у; например, при х = — 2 и при x =+2 значение у будет одно и то же, именно 4. Отрицательных значений для у никогда не получается.
в) Если абсолютная величина х неограниченно увеличивается, то и у неограниченно увеличивается. Так, если для х будем давать ряд неограниченно возрастающих положительных значений: 1, 2, 3, 4,… или ряд неограниченно убывающих отрицательных значений: -1, -2, -3, -4, … ,то для у получим ряд неограниченно возрастающих значений: 1, 4, 9, 16, 25, … .
Заметив эти свойства, составим таблицу значений функции у= x²; например, такую:
| x | … | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | … |
| у | … | 4 | 2,25 | 1 | 0,25 | 0 | 0,25 | 1 | 2,25 | 4 | … |
Изобразим теперь эти значения на чертеже 16 в виде точек, абсциссы которых будут выписанные значения х, а ординаты — соответствующие значения у (на чертеже за единицу длины мы приняли отрезок O1); полученные точки соединим кривой. Кривая эта называется параболой. Рассмотрим некоторые её свойства:
а) Вся кривая расположена по одну сторону от оси х-ов, именно — по ту сторону, по какую лежат положительные значения ординат.
б) Парабола разделяется осью у-ов на две части (ветви). Точка О, в которой эти ветви сходятся, называется вершиной параболы. Эта точка есть единственная общая точка параболы и оси х-ов.
в) Обе ветви бесконечны, так как х и у могут увеличиваться беспредельно. Ветви поднимаются от оси х-ов неограниченно вверх, удаляясь в то же время неограниченно от оси у-ов вправо и влево.
г) Ось у-ов служит для параболы осью симметрии, так что если перегнуть чертёж по этой оси так, чтобы левая половина чертежа упала на правую, то обе ветви совместятся; например, точка с абсциссой — 2 и с ординатой 4 совместится с точкой, имеющей абсциссу +2 и ту же ординату 4.
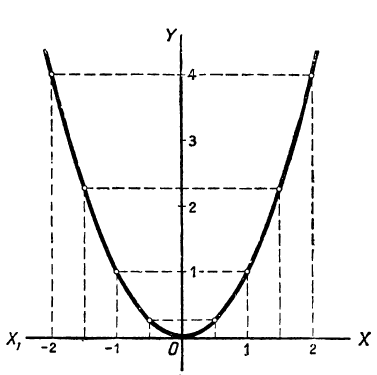
График функции у= x²
Предположим сначала, что а есть число положительное. Возьмём, например, такие две функции: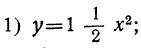
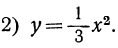
Составим таблицы значений этих функций, например такие:
1)
| x | -2 | -1 | 0 | 1 | 2 | … |
| у | 6 | 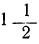 | 0 | 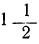 | 6 | … |
2)
| x | -3 | -2 | -1 | 0 | 1 | 2 | … |
| у | 3 | 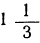 | 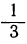 | 0 | 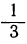 | 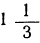 | … |
Нанесём все эти значения на чертёж 17 и проведём кривые. Для сравнения мы поместили на том же чертеже (прерывистой линией) ещё график функции: 3) y=x² .
3)
| x | -2 | -1 | 0 | 1 | 2 | … |
| y | 4 | 1 | 0 | 1 | 4 | … |
Из чертежа видно, что при одной и той же абсциссе ордината первой кривой в 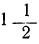 раза больше, а ордината второй кривой в 3 раза меньше, чем ордината третьей кривой. Эти кривые имеют общий характер: бесконечные ветви, ось симметрии и пр., только при α>1 ветви кривой более приподняты вверх, а при α<1 они более отогнуты книзу, чем у кривой y=x². Все такие кривые называются также параболами.
раза больше, а ордината второй кривой в 3 раза меньше, чем ордината третьей кривой. Эти кривые имеют общий характер: бесконечные ветви, ось симметрии и пр., только при α>1 ветви кривой более приподняты вверх, а при α<1 они более отогнуты книзу, чем у кривой y=x². Все такие кривые называются также параболами.
Предположим теперь, что коэффициент α будет число отрицательное. Пусть, например, 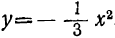 . Сравнивая эту функцию с функцией
. Сравнивая эту функцию с функцией 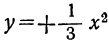 , замечаем, что при одном и том же значении х обе функции имеют одну и ту же абсолютную величину, но противоположны по знаку. Поэтому на чертеже 18 для функции
, замечаем, что при одном и том же значении х обе функции имеют одну и ту же абсолютную величину, но противоположны по знаку. Поэтому на чертеже 18 для функции 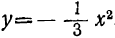 получится такая же парабола, как и для функции
получится такая же парабола, как и для функции 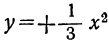 , только расположенная под осью х-ов симметрично с параболой
, только расположенная под осью х-ов симметрично с параболой 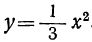 . В этом случае все значения функции отрицательны, кроме одного, равного нулю при х=0.
. В этом случае все значения функции отрицательны, кроме одного, равного нулю при х=0.
Замечание:
Если зависимость между двумя переменными величинами у и х выражается равенством y=ax² , где a — какое-нибудь постоянное число, то можно сказать, что величина у пропорциональна квадрату величины х, так как с увеличением или уменьшением х в 2 раза, в 3 раза и т. д. величина у увеличивается или уменьшается в 4 раза, в 9 раз, в 16 раз и т. д.
Например, площадь круга равна πR² , где R есть радиус круга и π — постоянное число; поэтому можно сказать, что площадь круга пропорциональна квадрату его радиуса.
График функции y=ax²+b
Пусть мы имеем следующие три функции: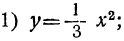
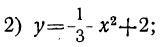
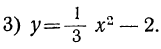
Очевидно, что при одном и том же значении аргумента х ордината второй функции больше, а ордината третьей функции меньше на 2 единицы, чем соответствующая ордината первой функции. Поэтому вторая и третья функции изобразятся на чертеже той же параболой, что и первая функция, только парабола эта должна быть поднята вверх (для второй функции) и опущена вниз (для третьей функции) на 2 единицы длины.
Вообще график функции y=ax²+b есть та же парабола, которая изображает функцию у=ax², только парабола эта должна быть поднята вверх, если b>0, опущена вниз, если b<0, на b единиц длины.
График трёхчлена второй степени
Сначала мы рассмотрим график такого трёхчлена, который может быть представлен в виде произведения a (x+m)² . Например, возьмём такие две функции: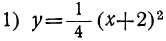 и
и 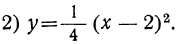
Для сравнения изобразим на том же чертеже ещё параболу: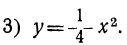
Предварительно составим таблицу частных значений этих трёх функций; например, такую:
| x= | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
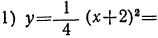 | 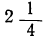 | 1 | 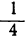 | 0 | 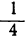 | 1 | 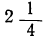 | 4 | 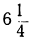 | 9 | 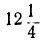 | 16 |
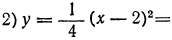 |  | 9 |  | 4 |  | 1 | 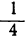 | 0 | 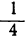 | 1 | 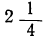 | 4 |
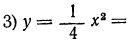 | 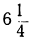 | 4 | 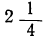 | 1 | 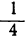 | 0 | 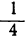 | 1 | 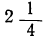 | 4 | 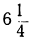 | 9 |
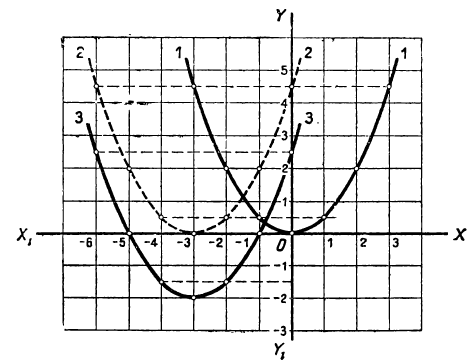
Нанеся все эти значения на чертёж, получим три графика, изображённые на чертеже 19.
Рассматривая этот чертёж, мы замечаем, что кривая 1 есть та же парабола 3, только перенесённая на 2 единицы влево, а кривая 2 есть та же парабола 3, но перенесённая на 2 единицы вправо.
Обобщая этот вывод, мы можем сказать, что график функции y=a(x+m)² есть парабола, изображающая функцию y=ax² , только парабола эта перенесена влево, если m>0, и в правд, если m<0, на столько единиц, сколько их заключается в абсолютной величине числа m. Ветви этой параболы направлены вверх, если α>0, как в наших примерах, и вниз, если α< 0, например как у параболы: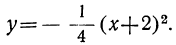
Теперь возьмём трёхчлен вида: y=ax²+bx+c. Рассмотрим, например, такой трёхчлен: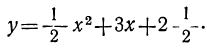
| x | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | … |
| y | 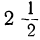 | 0 | 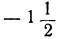 | -2 | 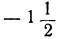 | 0 | 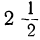 | 6 | … |
Построив точки, изображающие помещённые в таблице значения, и проведя через них кривую (кривая 3-я, черт. 20), мы получим искомый график. Покажем теперь, что этот график есть та же парабола, которая изображает функцию 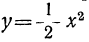 (полученную отбрасыванием в данном трёхчлене второго и третьего членов), только парабола эта перенесена в другое место. Для этого преобразуем данный трёхчлен следующим образом: во-первых, вынесем за скобки коэффициент при x²:
(полученную отбрасыванием в данном трёхчлене второго и третьего членов), только парабола эта перенесена в другое место. Для этого преобразуем данный трёхчлен следующим образом: во-первых, вынесем за скобки коэффициент при x²: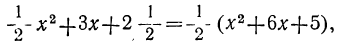
во-вторых, к трёхчлену, стоящему в скобках, добавим два взаимно уничтожающихся члена 9 и — 9: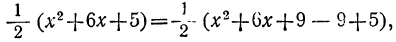
и, в-третьих, сгруппируем члены многочлена в две группы, получим: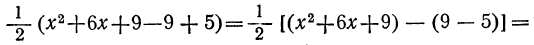
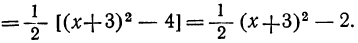
Принимая теперь во внимание примеры, разобранные выше, мы можем поступить так.
Построим параболу, изображающую функцию 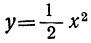 (кривая 1-я, черт. 20), затем перенесём её на 3 единицы влево, тогда получим 2-ю параболу, изображающую функцию
(кривая 1-я, черт. 20), затем перенесём её на 3 единицы влево, тогда получим 2-ю параболу, изображающую функцию 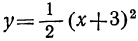 . Эту параболу перенесём теперь на 2 единицы вниз, тогда получим 3-ю параболу, изображающую данную функцию.
. Эту параболу перенесём теперь на 2 единицы вниз, тогда получим 3-ю параболу, изображающую данную функцию.
Графический способ решения квадратного уравнения
Квадратное уравнение можно графически решить таким способом:
построив на миллиметровой бумаге параболу, изображающую трёхчлен, стоящий в левой части уравнения, находим точки пересечения этой параболы с осью х-ов. Абсциссы этих точек и будут корни уравнения, так как при этих абсциссах ординаты, изображающие соответствующие значения трёхчлена, равны нулю.
Примеры: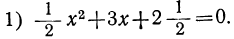
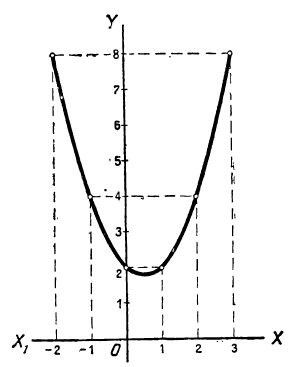
График левой части этого уравнения изображён кривой 3 (черт. 20). На нём мы видим, что парабола пересекается с осью х-ов в двух точках, абсциссы которых —1 и —5. Это и будут корни уравнения.
Это можно проверить, решив уравнение посредством общей формулы или путём подстановки.
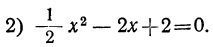
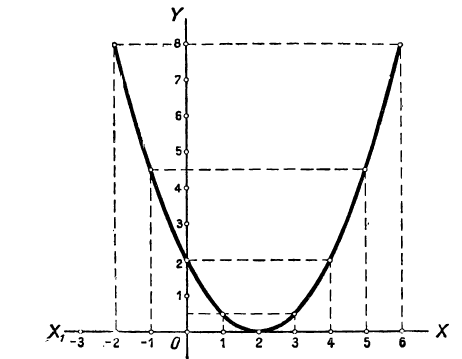
Составив таблицу частных значений трёхчлена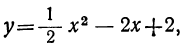
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| y | 8 | 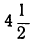 | 2 | 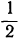 | 0 | 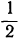 | 2 | 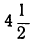 | 8 | … |
мы построим параболу (черт. 21). Эта парабола не пересекается с осью х-ов, а только её касается в точке с абсциссой 2. Уравнение в этом случае имеет только один корень 2 (точнее, два равных корня).
3) x² -x+2=0
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | 14 | 8 | 4 | 2 | 2 | 4 | 8 | 14 | … |
Парабола (черт. 22) не пересекается и не касается оси х-ов; уравнение не имеет вещественных корней.
Укажем ещё следующий приём графического решения квадратного уравнения. Пусть требуется решить уравнение:
x² — 1,5х — 2=0.
Представим его так:
x² =1,5x+2.
Каждая часть этого уравнения, рассматриваемая отдельно, есть некоторая функция от х. Обозначим функцию, выражаемую левой частью уравнения, буквой y₁ , а функцию, выражаемую правой частью уравнения, буквой у₂ . Первая функция на чертеже 23 изобразится параболой, а вторая — прямой. Построив на одном и том же чертеже графики этих двух функций, мы найдём, что прямая и парабола пересекаются в двух точках, абсциссы которых приблизительно выражаются числами 2,35 и — 0,85. Это и будут приближённые значения корней данного уравнения, так как при каждой из этих абсцисс ординаты y₁, у₂ равны между собой, и, следовательно, x² =l,5x+2.
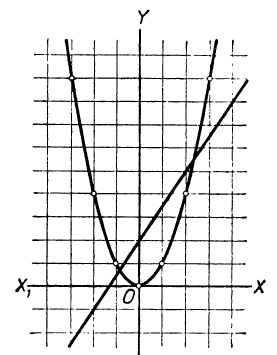
Если случится, что прямая с параболой не пересекается, то уравнение не имеет вещественных корней; если же прямая коснётся параболы, то уравнение имеет один корень, равный абсциссе точки касания.
Биквадратное уравнение
Уравнение четвёртой степени, например такое:
x⁴ — 13x² + 36=0,
в которое входят только чётные степени неизвестного, называется биквадратным. Оно приводится к квадратному, если заменим х² через у и, следовательно, x⁴ через у² ; тогда уравнение обратится в квадратное:
у² — 13y+36=0.
Решим его: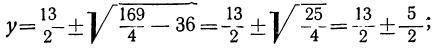
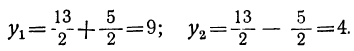
Но из равенства x²=y видно, что x=± √y. Подставляя сюда на место у найденные числа 9 и 4, получим следующие четыре решения данного уравнения:
x₁ = +√ 9 = 3;
x₂ = -√ 9 = -3;
x₃ = + √4 =2;
x₃ = — √4 = -2.
Составим формулы для решения биквадратного уравнения общего вида:
ax⁴ +bx² + c=0.
Положив x²=y, получим уравнение ay² + by + c=0, из которого находим: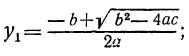
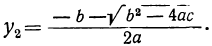
Но так как x=± √y , то для биквадратного уравнения мы получим следующие четыре решения: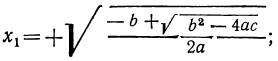
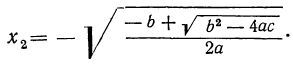
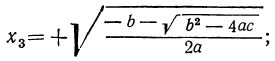
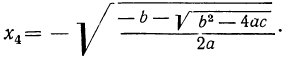
Отсюда видно, что если b² — 4ac < 0, то все четыре корня мнимы; если же b² —4ac>0, то могут быть три случая (мы полагаем a > 0):
1) все корни вещественные (как в приведённом выше численном примере), если 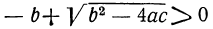 и
и 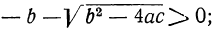
2) все корни мнимые, если оба эти выражения дадут отрицательные числа, и 3) два корня вещественные и два мнимые, если 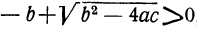 ,
, 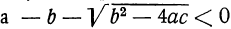 . Наконец, если b² — 4ac = 0 , то четыре корня попарно равны.
. Наконец, если b² — 4ac = 0 , то четыре корня попарно равны.
Уравнения, левая часть которых разлагается на множители, а правая есть нуль
Решение таких уравнений сводится к решению уравнений более низких степеней. Так, мы видели, что для решения неполного квадратного уравнения вида ax² + bx=0 достаточно его левую часть разложить на два множителя: x(ax + b) = 0 и затем, приняв во внимание, что произведение равно нулю только тогда, когда какой-нибудь сомножитель равен нулю, свести решение этого уравнения к решению двух уравнений первой степени: x=0 и ax + b=0.
Подобно этому можно решить неполное кубическое уравнение, не содержащее свободного члена; например, такое:
x³ + 3x² — 10x = 0.
Вынеся х за скобки, мы представим уравнение так:
x (x² +3x — 10) = 0,
из которых находим три решения: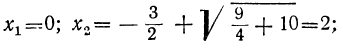
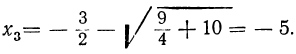
Пусть некоторое уравнение приведено к такому виду:
x(x+4)(x²-5x+6)=0.
Тогда оно распадается на три уравнения:
x = 0; x + 4 = 0; x² — 5x + 6 = 0
Уравнения эти дают:
х₁ = 0; x₂ = — 4; x₃ =2; x₄ = 3.
Двучленное уравнение
Двучленным уравнением называется уравнение вида 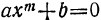 , или, что то же самое, вида
, или, что то же самое, вида 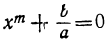 . Обозначив абсолютную величину числа
. Обозначив абсолютную величину числа 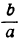 через q, мы можем двучленное уравнение записать или
через q, мы можем двучленное уравнение записать или 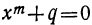 , или
, или 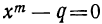 . При помощи вспомогательного неизвестного эти уравнения всегда можно упростить так, что свободный член у первого обратится в +1, а у второго в — 1. Действительно, положим, что
. При помощи вспомогательного неизвестного эти уравнения всегда можно упростить так, что свободный член у первого обратится в +1, а у второго в — 1. Действительно, положим, что 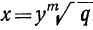 , где
, где 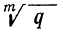 есть арифметический корень m-й степени из q; тогда
есть арифметический корень m-й степени из q; тогда 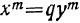 , и уравнения примут вид:
, и уравнения примут вид:
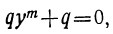 т.е.
т.е. 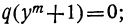 откуда
откуда 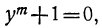
или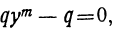 т.е.
т.е. 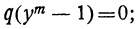 откуда
откуда 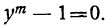
Итак, решение двучленных уравнений приводится к решению уравнений вида 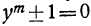 . Решение таких уравнений элементарными способами может быть выполнено только при некоторых частных значениях показателя m. Общий приём, употребляемый при этом, состоит в разложении левой части уравнения на множители, после чего уравнение приводится к виду, рассмотренному нами раньше.
. Решение таких уравнений элементарными способами может быть выполнено только при некоторых частных значениях показателя m. Общий приём, употребляемый при этом, состоит в разложении левой части уравнения на множители, после чего уравнение приводится к виду, рассмотренному нами раньше.
Решение двучленных уравнений третьей степени
Эти уравнения следующие: х³ —1=0 и х³ + l=0.
Заметив, что
х³ — 1 = х³ — 1³ = (х -1)(x²+ х +1)
и
х³ + 1 = х³ + 1³ = (х +1)(x²- х +1)
мы можем предложенные уравнения записать так:
(х -1)(x² + х +1) = 0 и ( х +1 ) ( x² — х +1)=0.
Значит, первое из них имеет своими корнями корни уравнений: x-1=0 и x²+ x +1=0, а второе — корни уравнений: x+1=0 и x²- x +1=0.
Решив их, находим, что уравнение х³ — 1=0 имеет следующие три корня: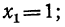
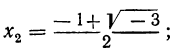
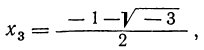
из которых один вещественный, а два мнимых; уравнение х³ + 1 = 0 имеет три корня:
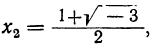
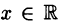
из которых также один вещественный и два мнимых.
Различные значения корня
Решение двучленных уравнений имеет тесную связь с нахождением всех значений корня (радикала) из данного числа. В самом деле, найти 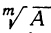 , очевидно, всё равно, что решить уравнение
, очевидно, всё равно, что решить уравнение 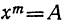 ,
, 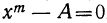 , и потому, сколько это уравнение имеет различных решений, столько
, и потому, сколько это уравнение имеет различных решений, столько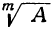 имеет различных решений.
имеет различных решений.
Основываясь на этом замечании, покажем, например, что корень кубичный из всякого вещественного числа (не равного нулю) имеет три различных значения.
Рассмотрим сначала случай положительного числа А. Пусть требуется найти 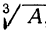 , т. е., другими словами, требуется решить уравнение х³-А=0. Обозначив арифметическое значение
, т. е., другими словами, требуется решить уравнение х³-А=0. Обозначив арифметическое значение 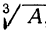 буквой q, положим, что x=qy. Тогда уравнение х³ — А=0 можно представить так: q³y³ — А = 0. Но q³=A, поэтому q³y³ — A=A( y³ — 1), и уравнение примет вид: y³ — 1=0.
буквой q, положим, что x=qy. Тогда уравнение х³ — А=0 можно представить так: q³y³ — А = 0. Но q³=A, поэтому q³y³ — A=A( y³ — 1), и уравнение примет вид: y³ — 1=0.
Мы видели, что это уравнение имеет три
корня: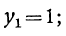
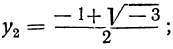
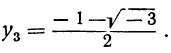
Каждое из этих значений, удовлетворяя уравнению y³ = l, представляет собой кубичный корень из 1. Так как x=qy, то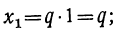
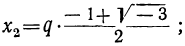
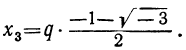
Это и будут три значения 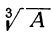 ; одно из них вещественное (арифметическое), а два — мнимые. Все они получатся, если арифметическое значение
; одно из них вещественное (арифметическое), а два — мнимые. Все они получатся, если арифметическое значение 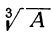 умножим на каждое из трёх значений
умножим на каждое из трёх значений 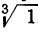 .
.
Например, кубичный корень из 8 имеет три следующих значения: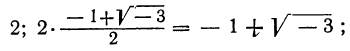
Если A<0, то предыдущее рассуждение остаётся в силе, только следует обозначить через q действительное значение 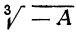 и положить x= — qy.
и положить x= — qy.
Трёхчленное уравнение
Так называется уравнение вида:
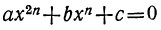
(частный случай такого вида при n=2 есть биквадратное уравнение). Оно приводится к квадратному, если введём вспомогательное неизвестное 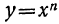 . Тогда уравнение примет вид:
. Тогда уравнение примет вид:
ay²+by+c=0,
откуда: 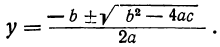
Следовательно: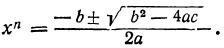
Решив, если возможно, это двучленное уравнение, найдём все значения х.
Пример:
x⁶- 9x³ + 8=0.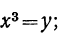
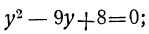
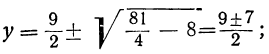
y₁=8; y₂=1;
следовательно:
x³=8 и x³=1.
Решив эти двучленные уравнения третьей степени, получим шесть значений для х: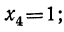
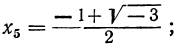
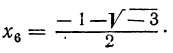
Системы уравнений второй степени
Степень уравнения с несколькими неизвестными: Чтобы определить степень уравнения, в которое входят несколько неизвестных, надо предварительно это уравнение упростить (раскрыть скобки, освободить от радикалов и знаменателей, которые содержат неизвестные, и сделать приведение подобных членов). Тогда степенью уравнения называется сумма показателей при неизвестных в том члене уравнения, в котором эта сумма наибольшая.
Например, три уравнения: x²+2xy—x+2=0, 3xy=4, 2x+y² — у=0 будут уравнениями второй степени с двумя неизвестными; уравнение 3x²y—y² + x+10 = 0 есть уравнение третьей степени (с двумя неизвестными) и т. п.
Заметим, что сумма показателей при неизвестных в каком-нибудь члене уравнения называется его измерением. Так, члены 2xy, 5x² , Зу² — второго измерения, члены 0,2x²y, 10xy² , 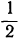 xyz — третьего измерения и т. п. Член, не содержащий неизвестных, называется членом нулевого измерения.
xyz — третьего измерения и т. п. Член, не содержащий неизвестных, называется членом нулевого измерения.
Заметим ещё, что уравнение называется однородным, если все его члены — одного и того же измерения. Так, 3x² + xy — 2y²=0 есть однородное уравнение второй степени с двумя неизвестными.
Мы рассмотрим сейчас, как решаются некоторые простейшие системы уравнений второй степени с двумя неизвестными.
Общий вид полного уравнения второй степени с двумя неизвестными есть следующий:
ax² +bxy+cy² +dx+ey+j=0.
В нём первые три члена — второго измерения, следующие два члена — первого и последний (свободный) член — нулевого. Коэффициенты а, b, с, … могут быть числами положительными, отрицательными, а также равными нулю (конечно, три коэффициента а, b и с не предполагаются одновременно равными нулю, так как в противном случае уравнение было бы не второй, а первой степени).
Мы рассмотрим сейчас, как решаются простейшие системы двух уравнений второй степени с двумя неизвестными.
Системы двух уравнений, из которых одно первой степени, а другое—второй
Пусть дана система: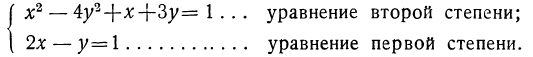
Всего удобнее такую систему решить способом подстановки следующим путём. Из уравнения первой степени определяем одно какое-нибудь неизвестное как функцию от другого неизвестного; например, определяем у как функцию от х:
y=2x — 1.
Тогда уравнение второй степени после подстановки даёт уравнение с одним неизвестным х:
x² — 4(2x — l)² + x +3(2x — 1) = 1;
x² — 4(4x² — 4x + l)+x+6x— 3=1;
x² — 16x² +16x — 4 + x + 6x — 3 — 1=0;
— 15 x² — 23x-8=0; 15x² — 23x + 8=0;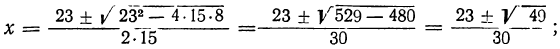
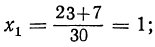
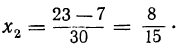
После этого из уравнения у=2х — 1 находим: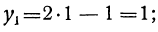
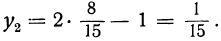
Таким образом, данная система имеет два решения: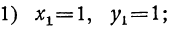
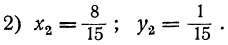
Искусственные приёмы:
Указанный приём применим в тех случаях, когда одно уравнение первой степени; в некоторых случаях можно пользоваться искусственными приёмами, для которых нельзя указать общего правила. Приведём примеры.
Пример:
x + y=α; xy=b.
Первый способ. Так как даны сумма и произведение неизвестных, то х и у должны быть корнями квадратного уравнения:
z² — az + b =0.
Следовательно: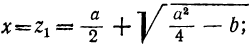
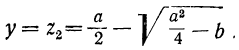
Второй способ. Возвысим первое уравнение в квадрат и вычтем из них учетверённое второе:
x²+ 2xy + y² = a² 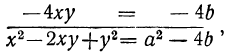
т.е.
(x-y)² =a²— 4b, откуда 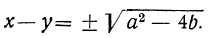
Теперь мы имеем систему: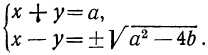
Складывая и вычитая эти уравнения, получим: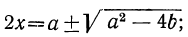
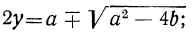
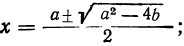
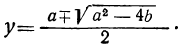
Так как одно из данных уравнений мы возвышали в квадрат, то проверяем подстановкой, нет ли посторонних корней в числе найденных.
Таким образом находим, что данная система имеет два решения: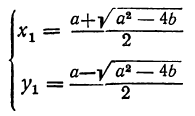 и
и 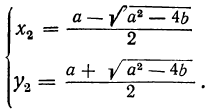
Второе решение отличается от первого только тем, что значение х в первом решении служит значением у во втором решении, и наоборот. Это можно было предвидеть, так как данные уравнения не изменяются от замены х на у, а у на х. Заметим, что такие уравнения называются симметричными.
Пример:
х — y= a, xy=b.
Первый способ. Представив уравнения в виде:
x +( —y)=а, x (-y)=-b,
замечаем, что х и —у это корни квадратного уравнения:
z² -az-b=0,
следовательно: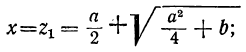
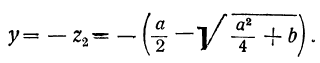
Второй способ. Возвысив первое уравнение в квадрат и сложив его с учетверённым вторым, получим:
(x + y)² = α² + 4b, откуда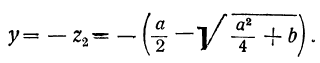
Теперь имеем систему: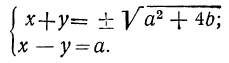
Пример:
x+y=cz, x² + y² = 6.
Возвысив первое уравнение в квадрат и вычтя из него второе, получим:
2xy= a² — b, откуда 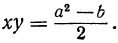
Теперь вопрос приводится к решению системы:
x + y= a, 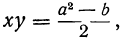
которую мы уже рассмотрели в первом примере.
Система двух уравнений, из которых каждое второй степени
Такая система в общем виде не разрешается элементарно, так как она приводится к полному уравнению четвёртой степени.
Рассмотрим некоторые частные виды уравнений, которые можно решить элементарным путём.
Пример:
x² +y² =α, ху=b.
Первый способ (способ подстановки). Из второго уравнения определяем одно неизвестное в зависимости от другого; например, 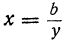 . Подставим это значение в первое уравнение и освободимся от знаменателя; тогда получим биквадратное уравнение:
. Подставим это значение в первое уравнение и освободимся от знаменателя; тогда получим биквадратное уравнение:
у⁴ — αy² + b² =0.
Решив его, найдём для у четыре значения. Подставив каждое из них в формулу, выведенную ранее для х, найдём четыре соответствующих значения для х.
Второй способ. Сложив первое уравнение с удвоенным вторым, получим:
x² +y² +2xy=α+2b, т. е. (x + y)² =a + 2b,
откуда: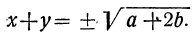
Вычтя из первого уравнения удвоенное второе, найдём:
x² +y² — 2xy=a — 2b, т. е. (х — у)² —а — 2b,
откуда: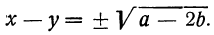
Таким образом, вопрос приводится к решению следующих четырёх систем первой степени: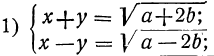
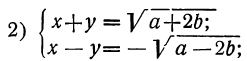
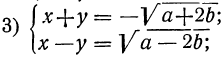
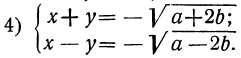
Каждая из них решается весьма просто посредством алгебраического сложения уравнений.
Третий способ. Возвысив второе уравнение в квадрат, получим следующую систему:
x² + y² =α, x²y² =b².
Отсюда видно, что x² и y² — корни квадратного уравнения:
z² + az+b² =0.
Следовательно: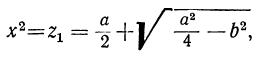
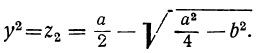
Пример:
x² — y² = a, xy=b.
Способом подстановки легко приведём эту систему к биквадратному уравнению. Вот ещё искусственный’приём решения этой системы.
Возвысив второе уравнение в квадрат, будем иметь систему:
x² — y² = a, x²y² = b².
или
x² +( — y²) = a , x² (- y²)=- b².
Отсюда видно, что x² и — y² будут корнями уравнения:
z² — az — b² = 0.
Следовательно: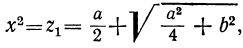
Отсюда найдём х и у.
Замечание:
Во всех случаях, когда приходится возводить уравнения в степень, необходима проверка корней.
Графический способ решения систем уравнений второй степени
Начертив графики каждого из данных уравнений, находим величины координат точек пересечения этих графиков; это и будут корни уравнений.
Пример:
Решить графически систему:
1) y=x² — 3x+2, 2)x = 2y² — 3.
Составим таблицу частных значений х и у для первого уравнения:
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
| y | … | 20 | 12 | 6 | 2 | 0 | 0 | 2 | 6 | 12 | … |
и таблицу частных значений х и у для второго уравнения:
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 15 | 5 | -1 | -3 | -1 | 5 | 15 | 29 | … |
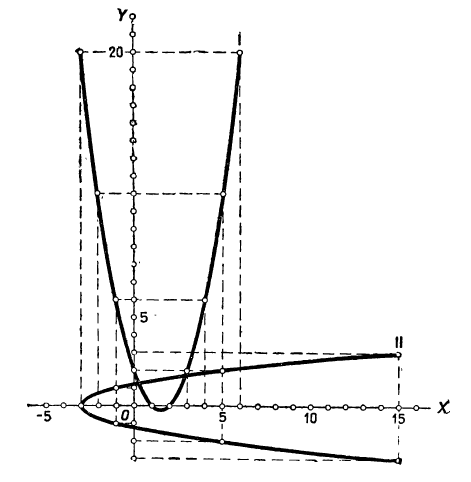
По этим значениям построим графики (эти графики будут параболы, черт. 24).
Графики пересекаются в двух точках, координаты которых приблизительно будут: х=0,3; y=1,3 и x=2,8; y=l,6.
Можно найти координаты точек пересечения точнее, если начертим в более крупном масштабе те части графиков, которые лежат около точек пересечения.
Квадратичная функция — основные понятия и определения
Функция — одно из важнейших математических понятий. Напомним, что функцией называют такую зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у.
Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Говорят также, что переменная у является функцией от переменной х. Значения зависимой переменной называют значениями функции.
Если зависимость переменной у от переменной х является функцией, то коротко это записывают так: y = f(x). (Читают: у равно / от х.) Символом / (х) обозначают значение функции, соответствующее значению аргумента, равному х.
Пусть, например, функция задается формулой 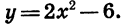 Тогда можно записать, что
Тогда можно записать, что 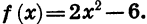 Найдем значения функции для значений х, равных, например, 1, 2,5, —3, т. е. найдем /(1), /(2,5), /(-3):
Найдем значения функции для значений х, равных, например, 1, 2,5, —3, т. е. найдем /(1), /(2,5), /(-3):
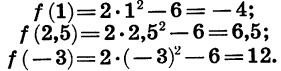
Заметим, что в записи вида y = f(x) вместо f употребляют и другие буквы: 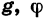 , и т. п.
, и т. п.
Все значения независимой переменной образуют область onределения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.
Если функция задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений аргумента, при которых формула имеет смысл. Например, областью определения функции 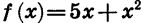 является множество всех чисел; областью определения функции
является множество всех чисел; областью определения функции 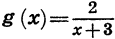 служит множество всех чисел, кроме — 3.
служит множество всех чисел, кроме — 3.
Область определения функции, описывающей реальный процесс, зависит от конкретных условий его протекания. Например, зависимость длины l железного стержня от температуры нагревания t выражается формулой 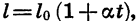 где
где 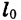 — начальная длина стержня, а
— начальная длина стержня, а 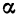 — коэффициент линейного расширения. Указанная формула имеет смысл при любых значениях t. Однако областью определения функции l = f (t) является промежуток в несколько десятков градусов, для которого справедлив закон линейного расширения.
— коэффициент линейного расширения. Указанная формула имеет смысл при любых значениях t. Однако областью определения функции l = f (t) является промежуток в несколько десятков градусов, для которого справедлив закон линейного расширения.
Напомним, что графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
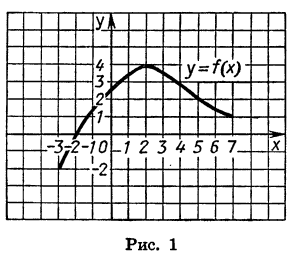
На рисунке 1 изображен график функции y = f(x), областью определения которой является промежуток [ — 3; 7]. С помощью графика можно найти, например, что f(— 3) = — 2, f(0) = 2,5, f(2) = 4, f(5) = 2. Наименьшее значение функции равно —2, а наибольшее равно 4; при этом любое число от —2 до 4 является значением данной функции. Таким образом, областью значений функции y = f(x) служит промежуток [-2; 4].
Мы изучили некоторые важные виды функций: линейную функцию, т. е. функцию, задаваемую формулой 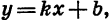 где k и b — некоторые числа; прямую пропорциональность — это частный случай линейной функции, она задается формулой
где k и b — некоторые числа; прямую пропорциональность — это частный случай линейной функции, она задается формулой 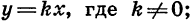 обратную пропорциональность — функцию
обратную пропорциональность — функцию 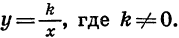
Графиком функции 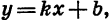 служит прямая (рис. 2). Ее областью определения является множество всех чисел. Область значений этой функции при
служит прямая (рис. 2). Ее областью определения является множество всех чисел. Область значений этой функции при 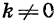 есть множество всех чисел, а при
есть множество всех чисел, а при 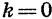 ее область значений состоит из одного числа b.
ее область значений состоит из одного числа b.
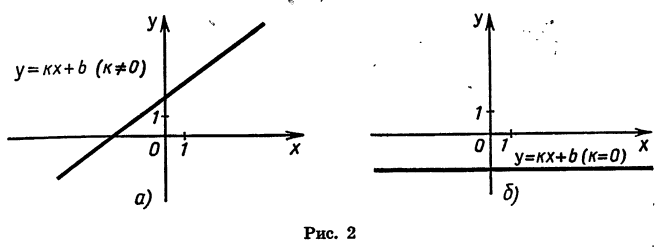
График функции 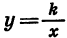 — называется гиперболой. На рисунке 3 изображен график функции
— называется гиперболой. На рисунке 3 изображен график функции 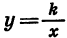 для
для  Область определения этой функции есть множество всех чисел, кроме нуля. Это множество является и областью ее значений.
Область определения этой функции есть множество всех чисел, кроме нуля. Это множество является и областью ее значений.
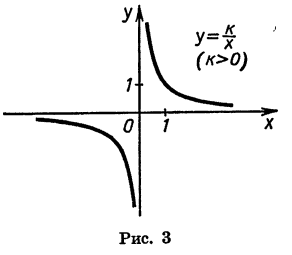
Функциями такого вида описываются многие реальные процессы и закономерности. Например, прямой пропорциональностью является зависимость массы тела m от его объема V при постоянной плотности 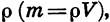 зависимость длины окружности С от ее радиуса
зависимость длины окружности С от ее радиуса 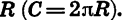 Обратной пропорциональностью является зависимость силы тока I на участке цепи от сопротивления проводника R при постоянном напряжении
Обратной пропорциональностью является зависимость силы тока I на участке цепи от сопротивления проводника R при постоянном напряжении 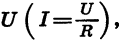 зависимость времени t, которое затрачивает равномерно движущееся тело на прохождение заданного пути s, от скорости движения
зависимость времени t, которое затрачивает равномерно движущееся тело на прохождение заданного пути s, от скорости движения 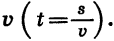
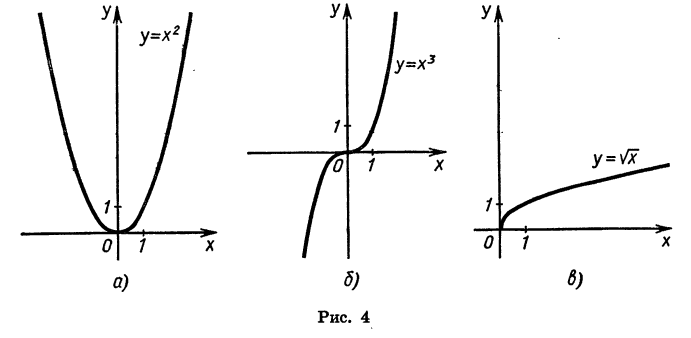
Мы рассматривали также функции, заданные формулами 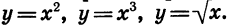 Их графики изображены на рисунке 4.
Их графики изображены на рисунке 4.
Рассмотрим еще одну функцию, а именно функцию, заданную формулой 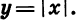
Так как выражение |х| имеет смысл при любом х, то областью определения этой функции является множество всех чисел. По определению |х| = х, если 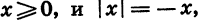 если x < 0. Поэтому функцию
если x < 0. Поэтому функцию 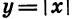 можно задать следующим образом:
можно задать следующим образом:
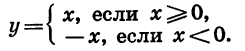
График рассматриваемой функции в промежутке 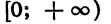
совпадает с графиком функции у = х, а в промежутке  — с графиком функции у = -х. График функции
— с графиком функции у = -х. График функции 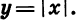 изображен на рисунке 5. Он состоит из двух лучей, исходящих из начала координат и являющихся биссектрисами I и II координатных углов.
изображен на рисунке 5. Он состоит из двух лучей, исходящих из начала координат и являющихся биссектрисами I и II координатных углов.
Свойства функции
На рисунке 9 изображен график зависимости температуры воздуха р (в °С) от времени суток t (в часах). Мы видим, что в 2 ч и в 8 ч температура равнялась нулю, от 0 до 2 ч и от 8 до 24 ч она была выше нуля, а от 2 до 8 ч — ниже нуля. Из графика ясно также, что в течение первых пяти часов температура понижалась, затем в промежутке от 5 до 14 ч она повышалась, а потом опять понижалась.
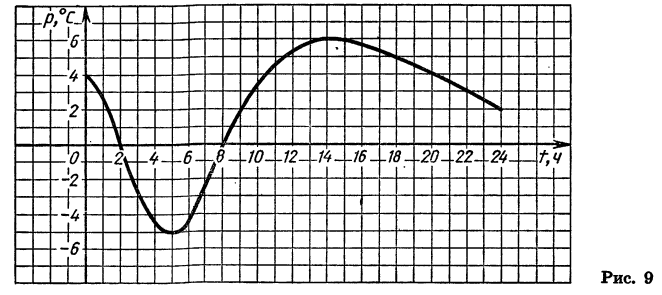
С помощью графика мы выяснили некоторые свойства функции p=f(t), где t — время суток в часах, а р — температура воздуха в градусах Цельсия.
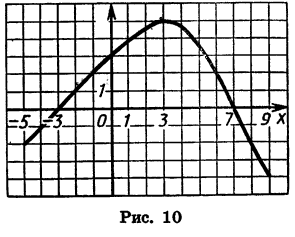
Рассмотрим теперь свойства функции y = f (х), график которой изображен на рисунке 10. Выясним сначала, при каких значениях х функция обращается в нуль, принимает положительные и отрицательные значения.
Найдем абсциссы точек пересечения графика с осью х. Получим х = — 3 и х = 7. Значит, функция принимает значение, равное нулю, при х = — 3 и х = 7. Значения аргумента, при которых функция обращается в нуль, называют нулями функции, т. е. числа -3 и 7 — нули рассматриваемой функции.
Нули функции разбивают ее область определения — промежуток [- 5; 9] на три промежутка: [-5; -3), (-3; 7) и (7; 9]. Для значений х из промежутка (-3; 7) точки графика расположены выше оси х, а для значений х из промежутков [- 5; — 3) и (7; 9] — ниже оси х. Значит, в промежутке ( — 3; 7) функция принимает положительные значения, а в каждом из промежутков [-5; -3) и (7; 9] — отрицательные.
Выясним теперь, как изменяются (увеличиваются или уменьшаются) значения данной функции с изменением х от — 5 до 9.
Из графика видно, что с увеличением х от -5 до 3 значения у увеличиваются, а с увеличением х от 3 до 9 значения у уменьшаются. Говорят, что в промежутке [-5; 3] функция y = f(x) является возрастающей, а в промежутке [3; 9] эта функция является убывающей.
Определение:
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции;
функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Иными словами, функцию y = f (х) называют возрастающей в некотором промежутке, если для любых 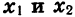 из этого промежутка, таких, что
из этого промежутка, таких, что  выполняется неравенство
выполняется неравенство
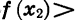
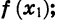 функцию y = f(x) называют убывающей в некотором промежутке, если для любых
функцию y = f(x) называют убывающей в некотором промежутке, если для любых 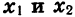 из этого промежутка, таких, что
из этого промежутка, таких, что  выполняется неравенство
выполняется неравенство 
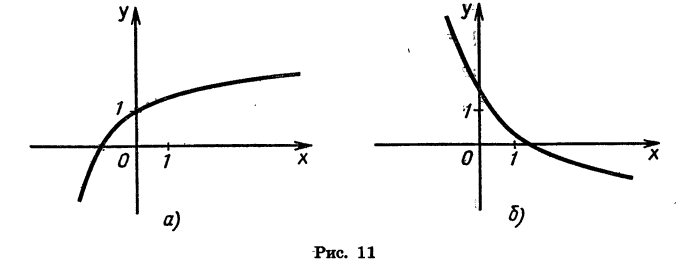
Если функция возрастает на всей области определения, то ее называют возрастающей функцией, а если убывает, то убывающей функцией. На рисунке 11 изображены графики возрастающей функции и убывающей функции.
Выясним, какими свойствами обладают некоторые изученные ранее функции.
Пример 1. Рассмотрим свойства функции  где
где 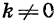 (рис. 12).
(рис. 12).
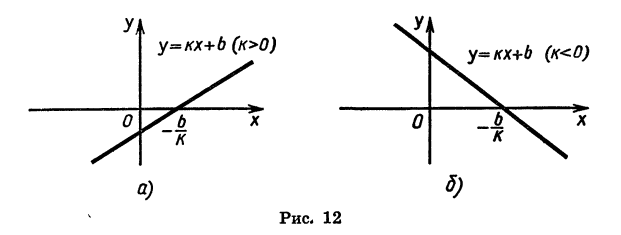
- Решив уравнение
 найдем, что
найдем, что  Значит, у=0, при
Значит, у=0, при 
- Выясним, при каких значениях х функция принимает положительные значения и при каких — отрицательные. Рассмотрим два случая:
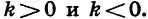
Пусть  Решив неравенство
Решив неравенство 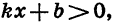 найдем, что
найдем, что 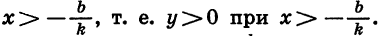 Из неравенства
Из неравенства 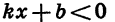 получим, что
получим, что 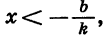 значит,
значит, 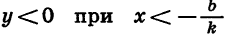 (см. рис. 12, а).
(см. рис. 12, а).
Пусть  Тогда, решив неравенства
Тогда, решив неравенства 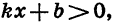 и
и 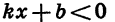 найдем, что
найдем, что 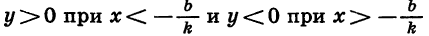 (см. рис. 12, б).
(см. рис. 12, б).
3. При  функция
функция 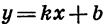 является возрастающей, а при
является возрастающей, а при  — убывающей.
— убывающей.
Докажем это. Пусть 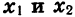 — произвольные значения аргумента, причем
— произвольные значения аргумента, причем  обозначим через
обозначим через 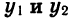 соответствующие им значения функции:
соответствующие им значения функции:
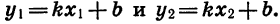
Рассмотрим разность 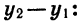
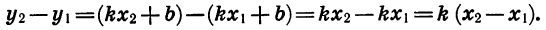
Множитель  положителен, так как
положителен, так как  Поэтому знак произведения
Поэтому знак произведения 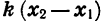 определяется знаком коэффициента k.
определяется знаком коэффициента k.
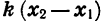
Если 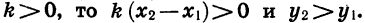 Значит, при
Значит, при  функция
функция 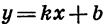 является возрастающей.
является возрастающей.
Если 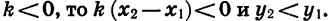 Значит, при
Значит, при 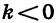 функция
функция 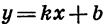 является убывающей.
является убывающей.
Пример:
Рассмотрим свойства функции 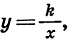 где
где 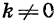 (рис. 13).
(рис. 13).
1.Так как дробь 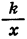 ни при каком значении х в нуль не обращается, то функция
ни при каком значении х в нуль не обращается, то функция 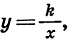 нулей не имеет.
нулей не имеет.
2. Если  , то дробь
, то дробь 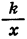 положительна при
положительна при 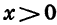 и отрицательна при
и отрицательна при 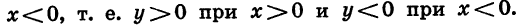
Если  то дробь
то дробь 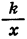 положительна при
положительна при 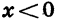 и отрицательна при
и отрицательна при 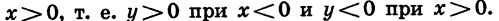
3. При  функция
функция 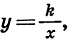 является убывающей в каждом
является убывающей в каждом
из промежутков 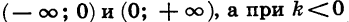 — возрастающей в каждом из этих промежутков (см. рис. 13, а, б).
— возрастающей в каждом из этих промежутков (см. рис. 13, а, б).
Доказательство этого свойства проводится аналогично тому, как это было сделано для линейной функции.
Заметим, что, хотя функция 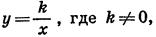 убывает (или возрастает) в каждом из промежутков
убывает (или возрастает) в каждом из промежутков 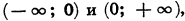 она не является убывающей (возрастающей) функцией на всей области определения.
она не является убывающей (возрастающей) функцией на всей области определения.
Квадратный трехчлен
Квадратный трехчлен и его корни
Выражение 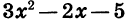 является многочленом второй степени с одной переменной. Такие многочлены называют квадратными трехчленами.
является многочленом второй степени с одной переменной. Такие многочлены называют квадратными трехчленами.
Определение:
Квадратным трехчленом называется многочлен вида 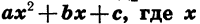 — переменная, а, b и с — некоторые числа, причем
— переменная, а, b и с — некоторые числа, причем 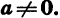
Значение квадратного трехчлена 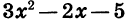 зависит от значения х. Так, например:
зависит от значения х. Так, например:
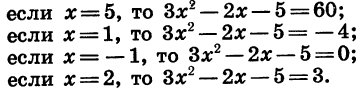
Мы видим, что при х = -1 квадратный трехчлен 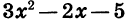 обращается в нуль. Говорят, что число — 1 является корнем этого трехчлена.
обращается в нуль. Говорят, что число — 1 является корнем этого трехчлена.
Корнем квадратного трехчлена называется значение переменной, при котором значение этого трехчлена равно нулю.
Для того чтобы найти корни квадратного трехчлена 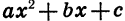 , надо решить квадратное уравнение
, надо решить квадратное уравнение 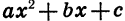 = 0.
= 0.
Пример:
Найдем корни квадратного трехчлена .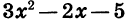 .
.
Решим уравнение
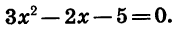
Имеем:
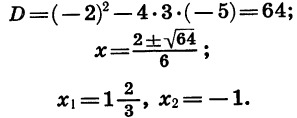
Значит, квадратный трехчлен 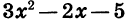 имеет два корня:
имеет два корня: 
Так как квадратный трехчлен 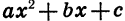 имеет те же корни, что и квадратное уравнение
имеет те же корни, что и квадратное уравнение 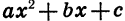 = 0, то он может, как и квадратное уравнение, иметь два корня, один корень или не иметь корней. Это зависит от знака дискриминанта квадратного уравнения
= 0, то он может, как и квадратное уравнение, иметь два корня, один корень или не иметь корней. Это зависит от знака дискриминанта квадратного уравнения 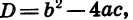 который называют также дискриминантом квадратного трехчлена. Если D > 0, то квадратный трехчлен имеет два корня; если D = 0, то квадратный трехчлен имеет один корень; если D < 0, то квадратный трехчлен не имеет корней.
который называют также дискриминантом квадратного трехчлена. Если D > 0, то квадратный трехчлен имеет два корня; если D = 0, то квадратный трехчлен имеет один корень; если D < 0, то квадратный трехчлен не имеет корней.
При решении задач иногда бывает удобно представлять квадратный трехчлен 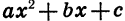 в виде
в виде 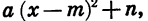 где m и n — некоторые числа. Такое преобразование называется выделением квадрата двучлена из квадратного трехчлена. Покажем на примере, как выполняется это преобразование.
где m и n — некоторые числа. Такое преобразование называется выделением квадрата двучлена из квадратного трехчлена. Покажем на примере, как выполняется это преобразование.
Пример:
Выделим из трехчлена 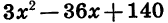 квадрат двучлена.
квадрат двучлена.
Вынесем за скобки множитель 3:
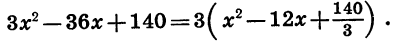
Преобразуем выражение в скобках. Для этого представим 12х в виде произведения 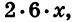 а затем прибавим и вычтем
а затем прибавим и вычтем 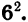 Получим:
Получим:
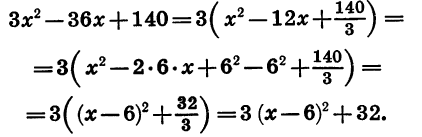
Значит,
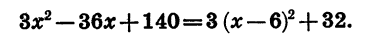
Рассмотрим задачу, при решении которой применяется выделение квадрата двучлена из квадратного трехчлена.
Пример:
Докажем, что из всех прямоугольников с периметром 20 см наибольшую площадь имеет квадрат.
Пусть одна сторона прямоугольника равна х см. Тогда другая сторона равна 10 — х см, а площадь прямоугольника равна 
Раскрыв скобки в выражении х (10 — х), получим 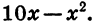 Выражение
Выражение 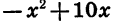 представляет собой квадратный трехчлен, в котором а = -1, b = 10, с = 0. Выделим квадрат двучлена:
представляет собой квадратный трехчлен, в котором а = -1, b = 10, с = 0. Выделим квадрат двучлена:
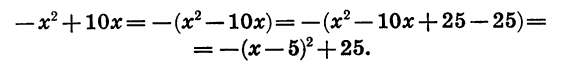
Так как выражение 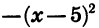 при любом
при любом 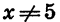 отрицательно, то сумма
отрицательно, то сумма 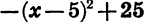 принимает наибольшее значение при x = 5. Значит, площадь будет наибольшей, когда одна из сторон прямоугольника равна 5 см. В этом случае вторая сторона также равна 5 см, т. е. прямоугольник является квадратом.
принимает наибольшее значение при x = 5. Значит, площадь будет наибольшей, когда одна из сторон прямоугольника равна 5 см. В этом случае вторая сторона также равна 5 см, т. е. прямоугольник является квадратом.
Разложение квадратного трехчлена на множители
Пусть требуется разложить на множители квадратный трехчлен 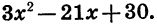 Вынесем сначала за скобки множитель 3. Получим:
Вынесем сначала за скобки множитель 3. Получим:
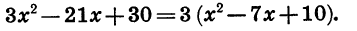
Для того чтобы разложить на множители трехчлен 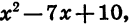 представим — 7х в виде суммы одночленов — 2х и — 5х и применим способ группировки:
представим — 7х в виде суммы одночленов — 2х и — 5х и применим способ группировки:
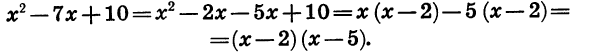
Значит,
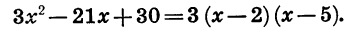
При х = 2 и х = 5 произведение 3 (х — 2) (х — 5), а следовательно, и трехчлен 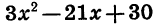 обращаются в нуль. Значит, числа 2 и 5 являются его корнями.
обращаются в нуль. Значит, числа 2 и 5 являются его корнями.
Мы представили квадратный трехчлен 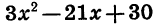 в виде произведения числа 3, т. е. коэффициента при
в виде произведения числа 3, т. е. коэффициента при 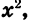 и двух линейных множителей. Первый из них представляет собой разность между переменной х и одним корнем трехчлена, а второй — разность между переменной х и другим корнем.
и двух линейных множителей. Первый из них представляет собой разность между переменной х и одним корнем трехчлена, а второй — разность между переменной х и другим корнем.
Такое разложение можно получить для любого квадратного трехчлена, имеющего корни. При этом считают, что если дискриминант квадратного трехчлена равен нулю, то этот трехчлен имеет два равных корня.
Теорема:
Если 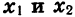 — корни квадратного трехчлена
— корни квадратного трехчлена 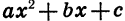 , то
, то
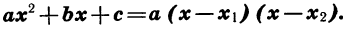
Доказательство.
Вынесем за скобки в многочлене 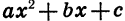 множитель а. Получим:
множитель а. Получим:
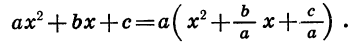
Так как корни квадратного трехчлена 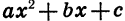 являются также корнями квадратного уравнения
являются также корнями квадратного уравнения 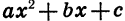 = 0, то по теореме Виета
= 0, то по теореме Виета
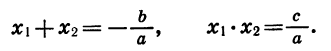
Отсюда
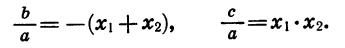
Поэтому
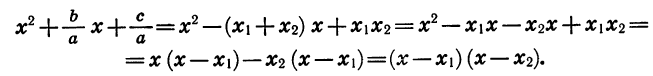
Итак,
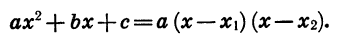
Заметим, что если квадратный трехчлен не имеет корней, то его нельзя разложить на множители, являющиеся многочленами первой степени.
Докажем это. Пусть трехчлен 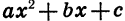 не имеет корней. Предположим, что его можно представить в виде произведения многочленов первой степени:
не имеет корней. Предположим, что его можно представить в виде произведения многочленов первой степени:
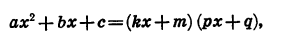
где 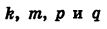 — некоторые числа, причем
— некоторые числа, причем 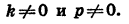
Произведение (kx+m) ( +q) обращается в нуль при 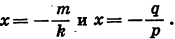
Следовательно, при этих значениях х обращается в нуль и трехчлен
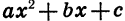 , т. е. числа
, т. е. числа 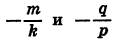 являются его корнями. Мы пришли к противоречию, так как по условию этот трехчлен корней не имеет.
являются его корнями. Мы пришли к противоречию, так как по условию этот трехчлен корней не имеет.
Пример:
Разложим на множители квадратный трехчлен 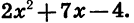
Решив уравнение 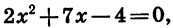 найдем корни трехчлена:
найдем корни трехчлена:
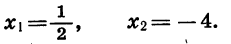
По теореме о разложении квадратного трехчлена на множители имеем:
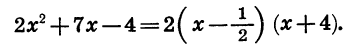
Полученный результат можно записать иначе, умножив число 2 на двучлен 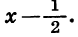 Получим:
Получим:
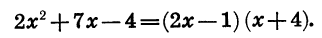
Пример:
Разложим на множители квадратный трехчлен 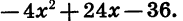
Решив уравнение 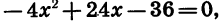 найдем корни трехчлена:
найдем корни трехчлена:
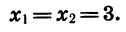
Значит,
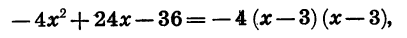
или иначе:
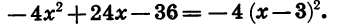
Пример:
Сократим дробь 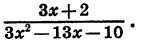
Разложим на множители квадратный трехчлен 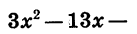 10. Его корни равны
10. Его корни равны 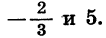 Поэтому
Поэтому
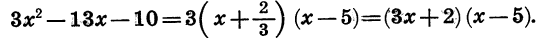
Значит,
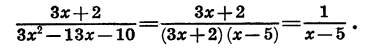
Квадратичная функция и ее график
Функция 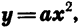 ее график и свойства
ее график и свойства
Одной из важных функций, которую мы будем рассматривать в дальнейшем, является квадратичная функция.
Определение:
Квадратичной функцией называется функция, которую можно задать формулой вида у = 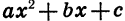 , где х — независимая переменная, а, b и с — некоторые числа, причем
, где х — независимая переменная, а, b и с — некоторые числа, причем 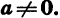
Примером квадратичной функции является зависимость пути от времени при равноускоренном движении. Если тело движется с ускорением 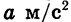 и к началу отсчета времени t прошло путь
и к началу отсчета времени t прошло путь 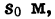 имея в этот момент скорость
имея в этот момент скорость 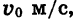 то зависимость пройденного пути s (в метрах) от времени t (в секундах) выражается формулой
то зависимость пройденного пути s (в метрах) от времени t (в секундах) выражается формулой
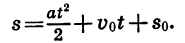
Если, например, а = 6, 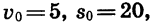 то формула примет вид:
то формула примет вид:
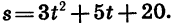
Изучение квадратичной функции мы начнем с частного случая — функции 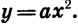
При а = 1 формула 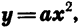 принимает вид
принимает вид 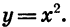 С этой функцией мы уже встречались. Ее графиком является парабола.
С этой функцией мы уже встречались. Ее графиком является парабола.
Построим график функции 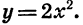 Составим таблицу значений этой функции:
Составим таблицу значений этой функции:

Построим точки, координаты которых указаны в таблице. Соединив их плавной линией, получим график функции 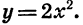 (рис. 20, а).
(рис. 20, а).
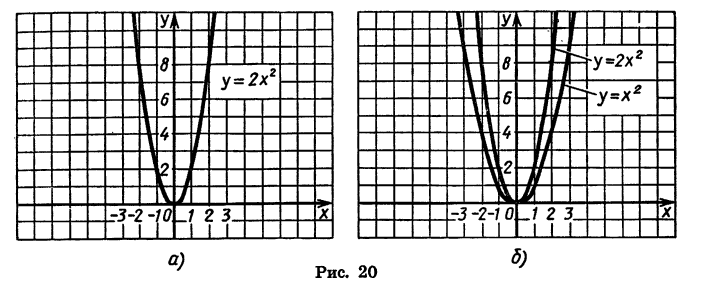
При любом 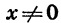 значение функции
значение функции  больше соответствующего значения функции
больше соответствующего значения функции  в 2 раза. Если переместить каждую точку графика функции
в 2 раза. Если переместить каждую точку графика функции 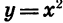 вверх так, чтобы расстояние от этой точки до оси х увеличилось в 2 раза, то она перейдет в точку графика функции
вверх так, чтобы расстояние от этой точки до оси х увеличилось в 2 раза, то она перейдет в точку графика функции 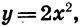 при этом каждая точка этого графика может быть получена из некоторой точки графика функции
при этом каждая точка этого графика может быть получена из некоторой точки графика функции 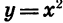 . Иными словами, график функции
. Иными словами, график функции 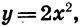 можно получить из параболы
можно получить из параболы 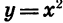 растяжением от оси х в 2 раза (рис. 20, б).
растяжением от оси х в 2 раза (рис. 20, б).
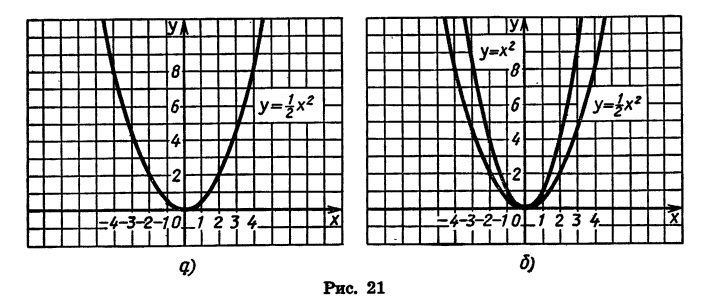
Построим теперь график функции 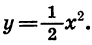 . Для этого составим таблицу ее значений:
. Для этого составим таблицу ее значений:

Построив точки, координаты которых указаны в таблице, и соединив их плавной линией, получим график функции 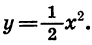 (рис. 21, а).
(рис. 21, а).
При любом 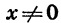 значение функции
значение функции 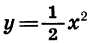 меньше соответствующего значения функции
меньше соответствующего значения функции 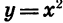 в 2 раза. Если переместить каждую точку графика функции
в 2 раза. Если переместить каждую точку графика функции 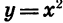 вниз так, чтобы расстояние от этой точки до оси х уменьшилось в 2 раза, то она
вниз так, чтобы расстояние от этой точки до оси х уменьшилось в 2 раза, то она
перейдет в точку графика функции 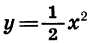 причем каждая точка этого графика может быть получена из некоторой точки графика функции
причем каждая точка этого графика может быть получена из некоторой точки графика функции 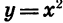 (рис. 21,6). Таким образом, график функции
(рис. 21,6). Таким образом, график функции 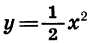 можно получить из параболы
можно получить из параболы 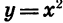 сжатием к оси х в 2 раза.
сжатием к оси х в 2 раза.
Вообще график функции 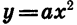 можно получить из параболы
можно получить из параболы 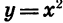 растяжением от оси х в а раз, если а > 1, и сжатием к оси х в
растяжением от оси х в а раз, если а > 1, и сжатием к оси х в 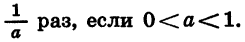
Рассмотрим теперь функцию 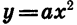 при а < 0.
при а < 0.
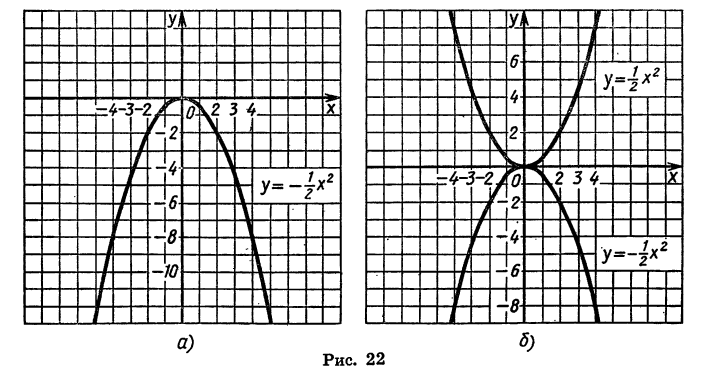
Построим график функции 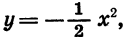 для чего составим таблицу значений этой функции:
для чего составим таблицу значений этой функции:

Воспользовавшись этой таблицей, построим график функции 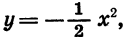 (рис. 22, а).
(рис. 22, а).
Сравним графики функций 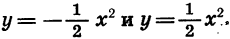 (рис. 22, б).
(рис. 22, б).
При любом х значения этих функций являются противоположными числами. Значит, соответствующие точки графиков симметричны относительно оси х. Иными словами, график функции
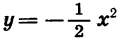 может быть получен из графика функции
может быть получен из графика функции 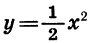 с помощью симметрии относительно оси х.
с помощью симметрии относительно оси х.
Вообще графики функций 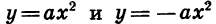 (при
(при  ) симметричны относительно оси х.
) симметричны относительно оси х.
График функции 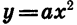 , где
, где 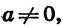 как и график функции
как и график функции 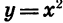 , называют параболой.
, называют параболой.
Сформулируем свойства функции 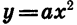 при а > 0.
при а > 0.
1.Если х = 0, то у = 0. График функции проходит через начало координат.
2. Если 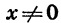 , то у > 0. График функции расположен в верхней полуплоскости.
, то у > 0. График функции расположен в верхней полуплоскости.
3. Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси у.
4. Функция убывает в промежутке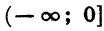 и возрастает в промежутке
и возрастает в промежутке 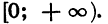
5. Наименьшее значение, равное нулю, функция принимает при х = 0, наибольшего значения функция не имеет. Областью значений функции является промежуток 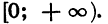
Докажем свойство 4. Пусть 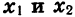 — два значения аргумента, причем
— два значения аргумента, причем 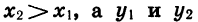 — соответствующие им значения функции. Составим разность
— соответствующие им значения функции. Составим разность 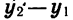 и преобразуем ее:
и преобразуем ее:
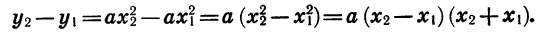
Так как 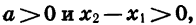 то произведение
то произведение 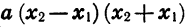 имеет тот же знак, что и множитель
имеет тот же знак, что и множитель 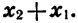 Если числа
Если числа 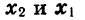 принадлежат промежутку
принадлежат промежутку 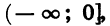 то этот множитель отрицателен. Если числа
то этот множитель отрицателен. Если числа 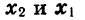 принадлежат промежутку
принадлежат промежутку 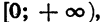 то множитель
то множитель 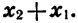 положителен. В первом случае
положителен. В первом случае 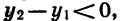 т. е.
т. е.  во втором случае
во втором случае 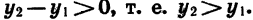 Значит, в промежутке
Значит, в промежутке 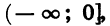 функция убывает, а в промежутке
функция убывает, а в промежутке 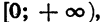 — возрастает.
— возрастает.
Теперь сформулируем свойства функции 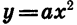 при а < 0.
при а < 0.
- Если х = 0, то у = 0. График функции проходит через начало координат.
- Если
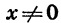 , то у < 0. График функции расположен в нижней полуплоскости.
, то у < 0. График функции расположен в нижней полуплоскости. - Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси у.
- Функция возрастает в промежутке
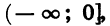 и убывает в промежутке
и убывает в промежутке 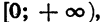
- Наибольшее значение, равное нулю, функция принимает при я = 0, наименьшего значения функция не имеет. Областью значений функции является промежуток
Доказательство свойства 4 проводится аналогично тому, как это было сделано для функции у=ах2 при а>0.
Из перечисленных свойств следует, что при а > 0 ветви параболы 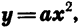 направлены вверх, а при а < 0 — вниз. Ось у является осью симметрии параболы. Точку пересечения параболы с ее осью симметрии называют вершиной параболы. Вершиной параболы
направлены вверх, а при а < 0 — вниз. Ось у является осью симметрии параболы. Точку пересечения параболы с ее осью симметрии называют вершиной параболы. Вершиной параболы 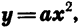 является начало координат.
является начало координат.
Построение графика, симметричного данному относительно оси х, растяжение графика от оси х или сжатие к оси х — различные виды преобразования графиков функций. Преобразования графиков, рассмотренные нами для функции 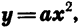 применимы к любой функции.
применимы к любой функции.
График функции y = -f(x) можно получить из графика функции y = f(х) с помощью симметрии относительно оси х.
График функции y = af (х) можно получить из графика функции y = f(x) с помощью растяжения от оси х в а раз, если а > 1, и с помощью сжатия к оси х в 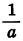 раз, если 0 < а < 1.
раз, если 0 < а < 1.
Графики функции 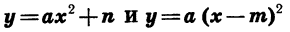
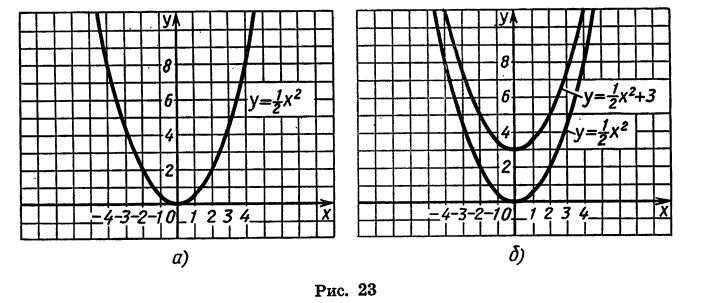
Рассмотрим другие частные случаи квадратичной функции. Пример 1. Выясним, что представляет собой график функции 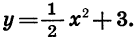
С этой целью в одной системе координат построим графики функций 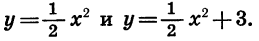 .
.
Составим таблицу значений функции 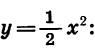

График функции 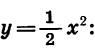 изображен на рисунке 23, а.
изображен на рисунке 23, а.
Чтобы получить таблицу значений функции 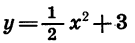 для тех же значений аргумента, достаточно к найденным | значениям функции
для тех же значений аргумента, достаточно к найденным | значениям функции 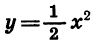 прибавить 3:
прибавить 3:

Построим точки, координаты которых указаны в таблице (2), и соединим их плавной линией. Получим график функции 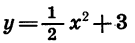 (рис. 23, б).
(рис. 23, б).
Легко понять, что каждой точке 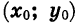 графика функции
графика функции 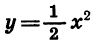 соответствует единственная точка
соответствует единственная точка 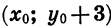 графика функции
графика функции 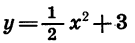 и наоборот. Значит, если переместить каждую точку графика функции
и наоборот. Значит, если переместить каждую точку графика функции 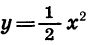 на 3 единицы вверх, то получим соответствующую точку графика функции
на 3 единицы вверх, то получим соответствующую точку графика функции 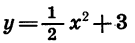 Иначе говоря, каждую точку второго графика можно получить из некоторой точки первого графика р помощью параллельного переноса на 3 единицы вверх вдоль оси у.
Иначе говоря, каждую точку второго графика можно получить из некоторой точки первого графика р помощью параллельного переноса на 3 единицы вверх вдоль оси у.
График функции 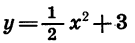 — парабола, полученная в результате сдвига вверх графика функции
— парабола, полученная в результате сдвига вверх графика функции 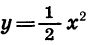 .
.
Вообще график функции 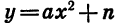 является параболой, которую можно получить из графика функции
является параболой, которую можно получить из графика функции 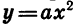 с помощью параллельного переноса вдоль оси у на п единиц вверх, если n > 0, или на -n единиц вниз, если
с помощью параллельного переноса вдоль оси у на п единиц вверх, если n > 0, или на -n единиц вниз, если 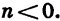
Пример:
Рассмотрим теперь функцию 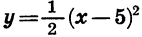 и выясним, что представляет собой ее график.
и выясним, что представляет собой ее график.
Для этого в одной системе координат построим графики функций 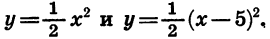
Для построения графика функции 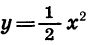 воспользуемся таблицей (1). Составим теперь таблицу значений функции
воспользуемся таблицей (1). Составим теперь таблицу значений функции 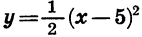 . При этом в качестве значений аргумента выберем те, которые на 5 больше соответствующих значений аргумента в таблице (1). Тогда соответствующие им значения функции
. При этом в качестве значений аргумента выберем те, которые на 5 больше соответствующих значений аргумента в таблице (1). Тогда соответствующие им значения функции 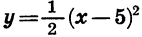 будут те же, которые записаны во второй строке таблицы (1):
будут те же, которые записаны во второй строке таблицы (1):

Построим график функции 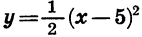 , отметив точки, координаты которых указаны в таблице (3) (рис. 24). Нетрудно заметить, что каждой точке
, отметив точки, координаты которых указаны в таблице (3) (рис. 24). Нетрудно заметить, что каждой точке 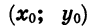 графика функции
графика функции
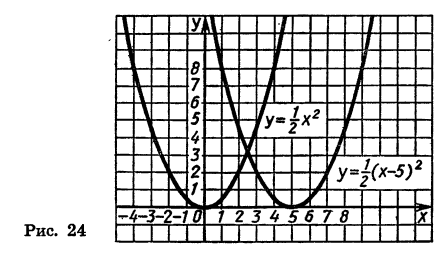
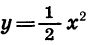 соответствует единственная точка
соответствует единственная точка 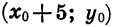 графика функции
графика функции 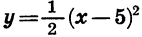 И наоборот.
И наоборот.
Значит, если переместить каждую точку графика функции 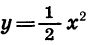 на 5 единиц вправо, то получим соответствующую точку графика функции
на 5 единиц вправо, то получим соответствующую точку графика функции 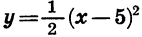 . Иначе говоря, каждую точку второго графика можно получить из некоторой точки первого графика с помощью параллельного переноса на 5 единиц вправо вдоль оси х.
. Иначе говоря, каждую точку второго графика можно получить из некоторой точки первого графика с помощью параллельного переноса на 5 единиц вправо вдоль оси х.
График функции 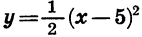 — парабола, полученная в результате сдвига вправо графика функции
— парабола, полученная в результате сдвига вправо графика функции 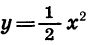 .
.
Вообще график функции 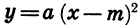 является параболой, которую можно получить из графика функции
является параболой, которую можно получить из графика функции 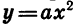 с помощью параллельного переноса вдоль оси х на m единиц вправо, если m > 0, или на -m единиц влево, если то m < 0.
с помощью параллельного переноса вдоль оси х на m единиц вправо, если m > 0, или на -m единиц влево, если то m < 0.
Полученные выводы позволяют понять, что представляет собой график функции 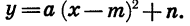 Рассмотрим, например, функцию
Рассмотрим, например, функцию 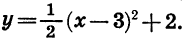 Ее график можно получить из графика функции
Ее график можно получить из графика функции 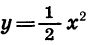 с помощью двух параллельных переносов — сдвига параболы
с помощью двух параллельных переносов — сдвига параболы 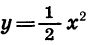 на 3 единицы вправо и на 2 единицы вверх (рис. 25).
на 3 единицы вправо и на 2 единицы вверх (рис. 25).
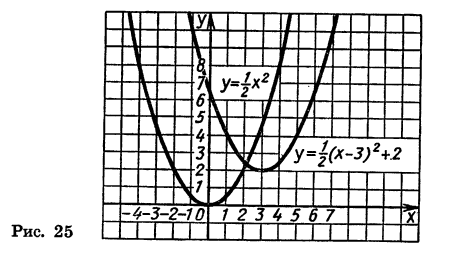
Вообще график функции 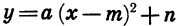 является параболой, которую можно получить из графика функции
является параболой, которую можно получить из графика функции 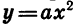 с помощью двух параллельных переносов: сдвига вдоль оси х на то единиц вправо, если m > 0, или на -m единиц влево, если m < 0, и сдвига вдоль оси у на n единиц вверх, если n > 0, или на -n единиц вниз, если n < 0.
с помощью двух параллельных переносов: сдвига вдоль оси х на то единиц вправо, если m > 0, или на -m единиц влево, если m < 0, и сдвига вдоль оси у на n единиц вверх, если n > 0, или на -n единиц вниз, если n < 0.
Заметим, что производить параллельные переносы можно в любом порядке: сначала выполнить параллельный перенос вдоль оси х, а затем вдоль оси у или наоборот.
Полученные нами выводы о преобразованиях графиков применимы к любым функциям.
График функции y=f(x) + n можно получить из графика функции у = f(x) с помощью параллельного переноса вдоль оси у на n единиц вверх, если n > 0, или на — n единиц вниз, если n < 0.
График функции y = f(x—m) можно получить из графика функции у = f(х) с помощью параллельного переноса вдоль оси х на m единиц вправо, если m > 0, или на —m единиц влево, если m < 0.
График функции y = f (х — m) + n можно получить из графика функции y = f(x) с помощью двух соответствующих параллельных переносов.
Построение графика квадратичной функции
Рассмотрим квадратичную функцию у = 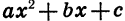 . Выделим из трехчлена
. Выделим из трехчлена 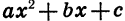 квадрат двучлена:
квадрат двучлена:
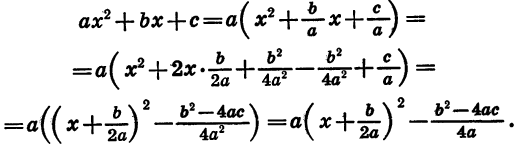
Отсюда
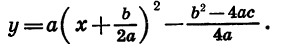
Мы получили формулу вида 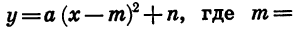
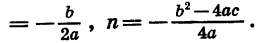
Значит, график функции 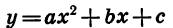 есть парабола, которую можно получить из графика функции
есть парабола, которую можно получить из графика функции 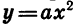 с помощью двух параллельных переносов — сдвига вдоль оси х и сдвига вдоль оси у. Отсюда следует, что график функции
с помощью двух параллельных переносов — сдвига вдоль оси х и сдвига вдоль оси у. Отсюда следует, что график функции 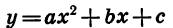 есть парабола, вершиной которой является точка
есть парабола, вершиной которой является точка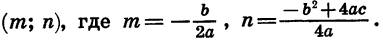 Осью симметрии параболы служит прямая х = m, параллельная оси у. При а > 0 ветви параболы направлены вверх, при а < 0 — вниз.
Осью симметрии параболы служит прямая х = m, параллельная оси у. При а > 0 ветви параболы направлены вверх, при а < 0 — вниз.
Чтобы построить график квадратичной функции, нужно:
1) найти координаты вершины параболы и отметить ее в координатной плоскости;
2) построить еще несколько точек, принадлежащих параболе;
3) соединить отмеченные точки плавной линией.
Заметим, что абсциссу т вершины удобно находить по формуле 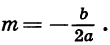 Ординату п можно находить, подставив найденное значение абсциссы в формулу
Ординату п можно находить, подставив найденное значение абсциссы в формулу 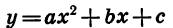 , так как при х = m
, так как при х = m
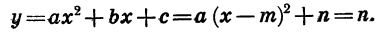
Приведем примеры построения графиков квадратичных функций.
Пример:
Построим график функции 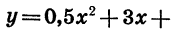 0,5.
0,5.
Графиком функции 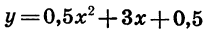 является парабола, ветви которой направлены вверх. Найдем координаты тип , вершины этой параболы:
является парабола, ветви которой направлены вверх. Найдем координаты тип , вершины этой параболы:
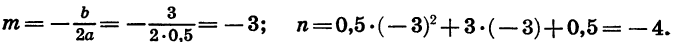
Значит, вершиной параболы является точка ( — 3; —4). Составим таблицу значений функции:

Построив точки, координаты которых указаны в таблице, и соединив их плавной линией, получим график функции 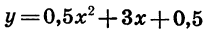 (рис. 27).
(рис. 27).
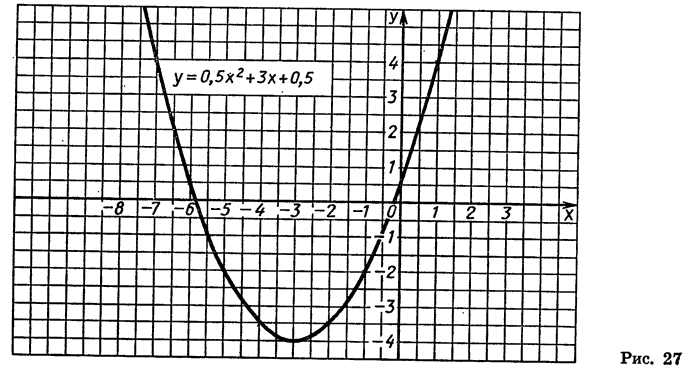
При составлении таблицы и построении графика учитывалось, что прямая х = — 3 является осью симметрии параболы. Поэтому мы брали точки с абсциссами — 4 и — 2, — 5 и — 1, — 6 и 0, симметричные относительно прямой х = — 3 (эти точки имеют одинаковые ординаты).
Пример:
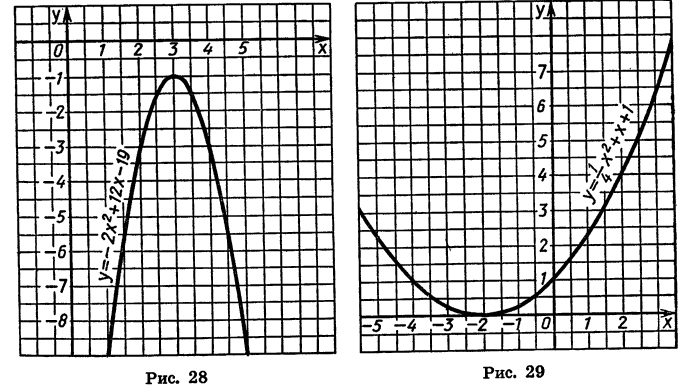
Построим график функции 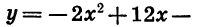 19.
19.
Графиком этой функции является парабола, ветви которой направлены вниз. Найдем координаты ее вершины:
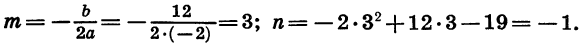
Вычислив координаты еще нескольких точек, получим таблицу:
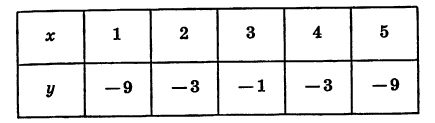
Соединив плавной линией точки, координаты которых указаны в таблице, получим график функции 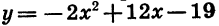 (рис. 28).
(рис. 28).
Пример:
Построим график функции 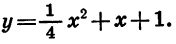
Графиком функции 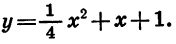 является парабола, ветви которой направлены вверх. Найдем координаты ее вершины:
является парабола, ветви которой направлены вверх. Найдем координаты ее вершины:
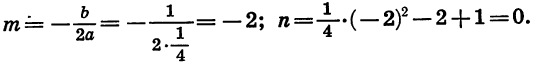
Вычислив координаты еще нескольких точек, получим таблицу:
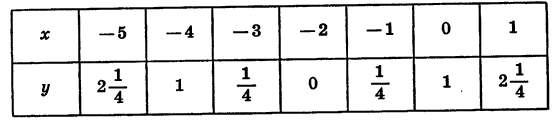
График функции 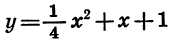 изображен на рисунке 29.
изображен на рисунке 29.
Решение неравенств второй степени с одной переменной
Неравенства вида 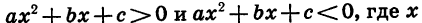 — переменная, a, b и с — некоторые числа, причем
— переменная, a, b и с — некоторые числа, причем 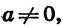 называют неравенствами второй степени с одной переменной.
называют неравенствами второй степени с одной переменной.
Решение неравенства второй степени с одной переменной можно рассматривать как нахождение промежутков, в которых соответствующая квадратичная функция принимает положительные или отрицательные значения.
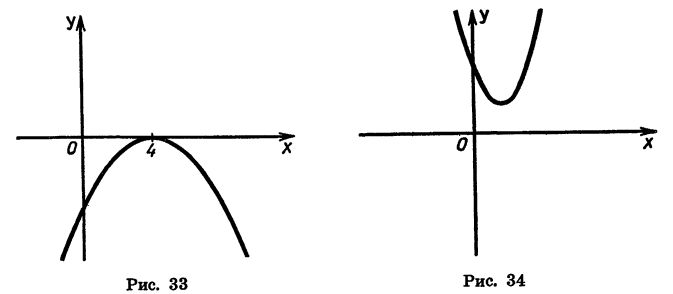
Пример:
Решим неравенство 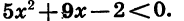
Рассмотрим функцию 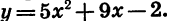 Графиком этой функции является-парабола, ветви которой направлены вверх.
Графиком этой функции является-парабола, ветви которой направлены вверх.
Выясним, как расположена эта парабола относительно оси х. Для этого решим уравнение 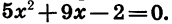
Получим:

Значит, парабола пересекает ось х в двух точках, абсциссы которых равны 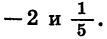
Покажем схематически, как расположена парабола в координатной плоскости (рис. 31). Из рисунка видно, что функция принимает отрицательные значения, когда 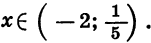
Следовательно, множеством решений неравенства 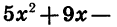 2 < 0 является числовой промежуток
2 < 0 является числовой промежуток 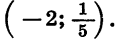
Заметим, что при рассмотренном способе решения неравенства нас не интересовала вершина параболы. Важно лишь было знать, куда направлены ветви параболы — вверх или вниз и каковы абсциссы точек ее пересечения с осью х.
Пример:
Решим неравенство 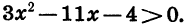
График функции 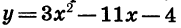 — парабола, ветви которой направлены вверх.
— парабола, ветви которой направлены вверх.
Для того чтобы выяснить, пересекает ли парабола ось х и в каких точках, решим уравнение 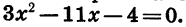 Получим, что
Получим, что
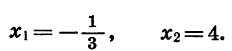
Покажем схематически, как расположена парабола в координатной плоскости (рис. 32). Из рисунка видно, что данное неравенство верно, если х принадлежит промежутку 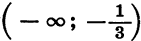 или промежутку
или промежутку 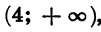 т. е. множеством решений неравенства
т. е. множеством решений неравенства
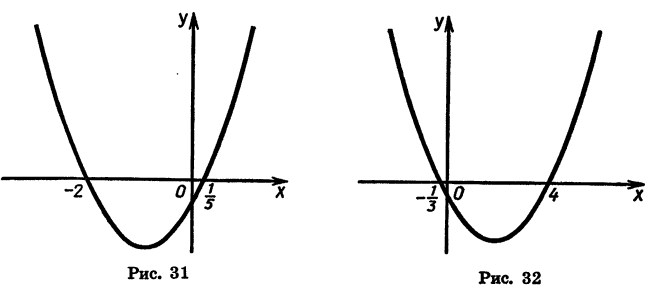
является объединение промежутков 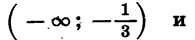
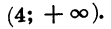
Ответ можно записать так: 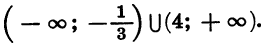
Пример:
Решим неравенство 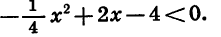
Рассмотрим функцию  Ее графиком является парабола, ветви которой направлены вниз.
Ее графиком является парабола, ветви которой направлены вниз.
Выясним, как расположен график относительно оси х. Решим для этого уравнение 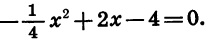 Получим, что х = 4. Уравнение имеет единственный корень. Значит, парабола касается оси х.
Получим, что х = 4. Уравнение имеет единственный корень. Значит, парабола касается оси х.
Изобразив схематически параболу (рис. 33), найдем, что функция принимает отрицательные значения при любом х, кроме 4.
Ответ можно записать так: х — любое число, не равное 4.
Пример:
Решим неравенство 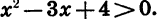
График функции 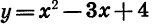 — парабола, ветви которой направлены вверх.
— парабола, ветви которой направлены вверх.
Чтобы выяснить, как расположена парабола относительно оси х, решим уравнение 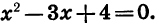 Находим, что D = -7 < 0, т. е. это уравнение не имеет корней. Значит, парабола не имеет общих точек с осью х.
Находим, что D = -7 < 0, т. е. это уравнение не имеет корней. Значит, парабола не имеет общих точек с осью х.
Показав схематически расположение параболы в координатной плоскости (рис. 34), найдем, что функция принимает положительные значения при любом х.
Ответ: х — любое число.
Итак, для решения неравенств вида 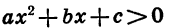 и
и 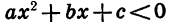 поступают следующим образом:
поступают следующим образом:
1) находят дискриминант квадратного трехчлена и выясняют, имеет ли трехчлен корни
2) если трехчлен имеет корни, то отмечают их на оси х и через отмеченные точки проводят схематически параболу, ветви которой направлены вверх при а > 0 или вниз при а < 0;
если трехчлен не имеет корней, то схематически изображают параболу, расположенную в верхней полуплоскости при а > 0 или в нижней при а < 0;
3) находят на оси х промежутки, для которых точки параболы расположены выше оси х (если решают неравенство 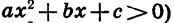 или ниже оси х (если решают неравенство
или ниже оси х (если решают неравенство 
Решение неравенств методом интервалов
Рассмотрим функцию
Областью определения этой функции является множество всех чисел. Нулями функции служат числа — 2, 3, 5. Они разбивают область определения функции на промежутки 

Выражение (х + 2) (х — 3) (х — 5) представляет собой произведение трех множителей. Знак каждого из этих множителей в рассматриваемых промежутках указан в таблице:
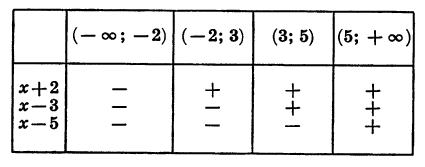
Отсюда ясно, что:
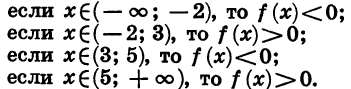
Мы видим, что в каждом из промежутков 
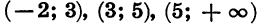 функция сохраняет знак, а при переходе через точки — 2, 3 и 5 ее знак изменяется (рис. 35,6). Вообще, пусть функция задана формулой вида
функция сохраняет знак, а при переходе через точки — 2, 3 и 5 ее знак изменяется (рис. 35,6). Вообще, пусть функция задана формулой вида
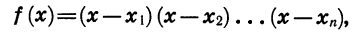
где х — переменная, а  не равные друг другу числа. Числа
не равные друг другу числа. Числа  являются нулями функции. В каждом из промежутков, на которые область определения разбивается нулями функции, знак функции сохраняется, а при переходе через нуль ее знак изменяется.
являются нулями функции. В каждом из промежутков, на которые область определения разбивается нулями функции, знак функции сохраняется, а при переходе через нуль ее знак изменяется.
Это свойство используется для решения неравенств вида
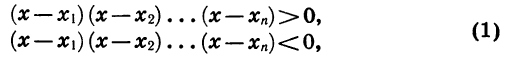
где  не равные друг другу числа.
не равные друг другу числа.
Пример:
Решим неравенство
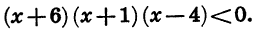
Данное неравенство является неравенством вида (1), так как в левой части записано произведение 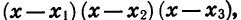 где
где 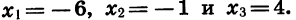 Для его решения удобно воспользоваться рассмотренным выше свойством чередования знаков функции.
Для его решения удобно воспользоваться рассмотренным выше свойством чередования знаков функции.
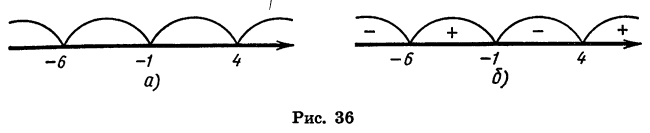
Отметим на координатной прямой нули функции
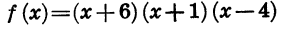
Найдем знаки этой функции в каждом из промежутков 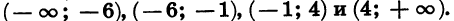 Для этого достаточно знать, какой знак имеет функция в одном из этих промежутков, и, пользуясь свойством чередования знаков, определить знаки во всех остальных промежутках. При этом удобно начинать с крайнего справа промежутка
Для этого достаточно знать, какой знак имеет функция в одном из этих промежутков, и, пользуясь свойством чередования знаков, определить знаки во всех остальных промежутках. При этом удобно начинать с крайнего справа промежутка 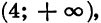 так как в нем значение функции
так как в нем значение функции 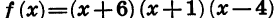 заведомо положительно. Это объясняется тем, что при значениях х, расположенных правее всех нулей функции, каждый из множителей
заведомо положительно. Это объясняется тем, что при значениях х, расположенных правее всех нулей функции, каждый из множителей 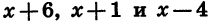 положителен. Используя свойство чередования знаков, определим, двигаясь по координатной прямой справа налево, знаки данной функции в каждом из остальных промежутков (рис. 36, б).
положителен. Используя свойство чередования знаков, определим, двигаясь по координатной прямой справа налево, знаки данной функции в каждом из остальных промежутков (рис. 36, б).
Из рисунка видно, что множеством решений неравенства является объединение промежутков 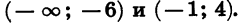
Ответ: 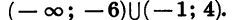
Рассмотренный способ решения неравенств называют методом интервалов.
Рассмотрим теперь примеры решения неравенств, которые сводятся к неравенствам вида (1).
Пример:
Решим неравенство 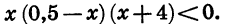
Приведем данное неравенство к виду (1). Для этого в двучлене 0,5 — х вынесем за скобку множитель -1. Получим:
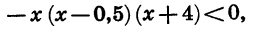
отсюда
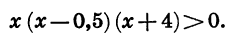
Мы получили неравенство вида (1), равносильное данному.

Отметим на координатной прямой нули функции f (х) = х (х — 0,5)(х + 4) (рис. 37, а). Покажем знаком «плюс», что в крайнем справа промежутке функция принимает положительное значение, а затем, двигаясь справа налево, укажем знак функции в каждом из промежутков (рис. 37, б). Получим, что множеством решений неравенства является объединение промежутков 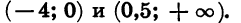
Ответ: 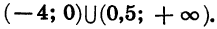
Пример:
Решим неравенство 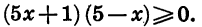
Приведем неравенство к виду (1). Для этого в первом двучлене вынесем за скобки множитель 5, а во втором —1, получим:
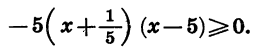
Разделив обе части неравенства на -5, будем иметь:
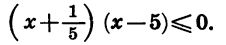
Отметим на координатной прямой нули функции f(x) 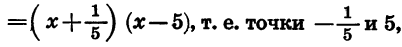 и укажем знаки функции в образовавшихся промежутках (рис. 38). Мы видим, что множество решении неравенства состоит из чисел
и укажем знаки функции в образовавшихся промежутках (рис. 38). Мы видим, что множество решении неравенства состоит из чисел 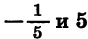 и чисел, заключенных между ними, т. е. представляет собой промежуток
и чисел, заключенных между ними, т. е. представляет собой промежуток
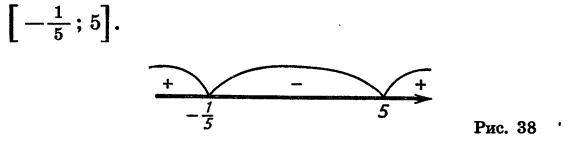
Ответ: 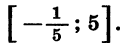
Заметим, что данное неравенство можно решить иначе, воспользовавшись свойствами графика квадратичной функции.
7_у
Пример:
Решим неравенство 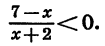
Так как знак дроби 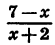 совпадает со знаком произведения (7—х)(х+2), то данное неравенство равносильно неравенству
совпадает со знаком произведения (7—х)(х+2), то данное неравенство равносильно неравенству 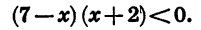
Приведя неравенство 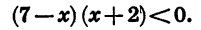 к виду (1) и используя метод интервалов, найдем, что множеством решений этого неравенства, а значит, и данного неравенства
к виду (1) и используя метод интервалов, найдем, что множеством решений этого неравенства, а значит, и данного неравенства 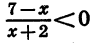 является объединение промежутков
является объединение промежутков 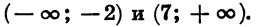
Ответ: 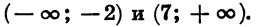
Квадратичная функция и её построение
Парабола
Рассмотрим уравнение

Если х и у рассматривать как координаты точки, то уравнение (1) определит некоторое геометрическое место точек. Исследуем вид этого геометрического места. Заметим, что наше исследование будет неполным, так как останутся вопросы, которые нами пока не будут выяснены. Чем дальше мы будем продвигаться в изучении математики, тем полнее будут проводиться исследования.
1) Так как 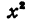 при любом значении х всегда неотрицательно, то у, определяемое уравнением всегда неотрицательно. Значит, любая точка, принадлежащая изучаемому геометрическому месту, не будет лежать ниже оси Ох (рис. 18).
при любом значении х всегда неотрицательно, то у, определяемое уравнением всегда неотрицательно. Значит, любая точка, принадлежащая изучаемому геометрическому месту, не будет лежать ниже оси Ох (рис. 18).
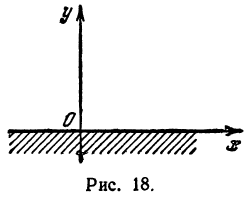
2) Так как и для —х и для х после возведения в квадрат получается одно и то же число, то точки, принадлежащие геометрическому месту и соответствующие значениям — х и х, имеют одну и ту же ординату и поэтому расположены симметрично относительно оси Оу (рис. 19).
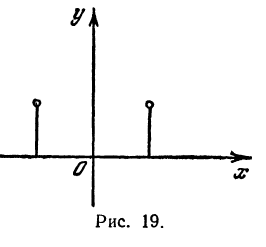
3) Если х положительно, то, чем больше х, тем больше и 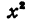 . Поэтому по мере возрастания абсолютной величины абсциссы величина ординаты тоже возрастает. Следовательно точки геометрического места удаляются от начала координат вправо вверх и влево вверх.
. Поэтому по мере возрастания абсолютной величины абсциссы величина ординаты тоже возрастает. Следовательно точки геометрического места удаляются от начала координат вправо вверх и влево вверх.
Геометрическое место, определяемое уравнением 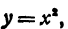 называется параболой и имеет вид, изображенный на рис. 20. Эту кривую линию называют также графиком функции
называется параболой и имеет вид, изображенный на рис. 20. Эту кривую линию называют также графиком функции 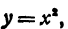 Точка (0, 0) принадлежит геометрическому месту, поэтому можно сказать, что парабола проходит через начало координат. Эту точку называют вершиной параболы. Часть параболы, расположенная в первой четверти, и часть параболы, расположенная во второй четверти, называются ее ветвями.
Точка (0, 0) принадлежит геометрическому месту, поэтому можно сказать, что парабола проходит через начало координат. Эту точку называют вершиной параболы. Часть параболы, расположенная в первой четверти, и часть параболы, расположенная во второй четверти, называются ее ветвями.
Теперь рассмотрим уравнение
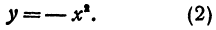
Оно определяет геометрическое место точек. Сравнивая уравнения (1) и (2), замечаем, что при одном и том же х значения у отличаются только знаками, именно у, полученный из уравнения (2), всегда неположителен. Поэтому уравнение (2) тоже определяет параболу, вершина которой также находится в точке (0, 0), но ветви этой которой также находится в точке (0, 0), но ветви этой параболы идут от начала координат вниз вправо и вниз влево. График функции (2) изображен на рис. 21
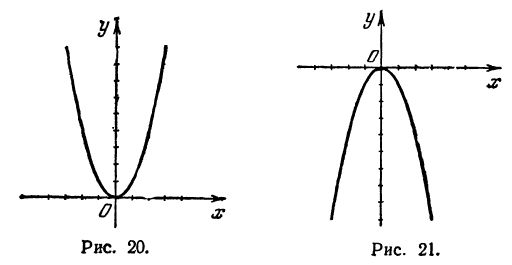
Перейдем к рассмотрению уравнения

Сравним его с уравнением (1),
Если а положительно и больше единицы, то очевидно, что при одном и том же значении х величина у из уравнения (3) будет больше, чем величина у, взятая из уравнения (1). Отсюда можно заключить, что кривая, определяемая уравнением (3), отличается от параболы (1) только тем, что ординаты ее точек растянуты в а раз. Таким образом, кривая, определяемая уравнением (3), является более сжатой, чем парабола 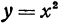 . Эту кривую тоже называют параболой.
. Эту кривую тоже называют параболой.
Если 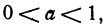 то получим параболу более раскрытую, чем парабола
то получим параболу более раскрытую, чем парабола 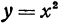 . Для а отрицательного получаем аналогичные выводы, которые ясны из рис. 22.
. Для а отрицательного получаем аналогичные выводы, которые ясны из рис. 22.
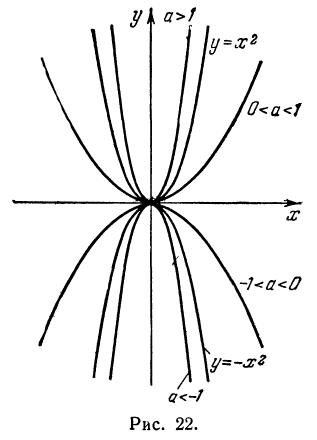
Теперь покажем, что кривая, определяемая уравнением
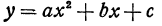
является параболой, только ее расположение относительно координатных осей другое, чем в разобранных случаях. Предварительно рассмотрим параллельный перенос осей координат.
Параллельный перенос осей координат
Пусть на плоскости дана система координат хОу (рис. 23). Рассмотрим новую систему координат  .Предположим, что новая ось
.Предположим, что новая ось  параллельна старой оси Ох и новая ось
параллельна старой оси Ох и новая ось  параллельна старой оси Оу. Начало координат новой системы — точка
параллельна старой оси Оу. Начало координат новой системы — точка  . Масштаб и направление осей одинаковы в старой и новой системах координат.
. Масштаб и направление осей одинаковы в старой и новой системах координат.
Обозначим координаты нового начала  относительно старой системы координат через х0 и у0, так что
относительно старой системы координат через х0 и у0, так что
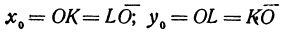
Возьмем произвольную точку М на плоскости; пусть ее координаты в старой системе будут х и у, а в новой 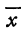 и
и 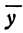 . Тогда
. Тогда
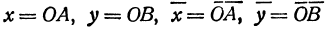
и (на основании формулы (2) из § 1 гл. I)
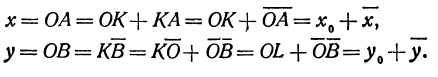
Таким образом,

Переход от старой системы координат к указанной новой называется параллельным переносом или параллельным сдвигом осей координат. Приходим к выводу:
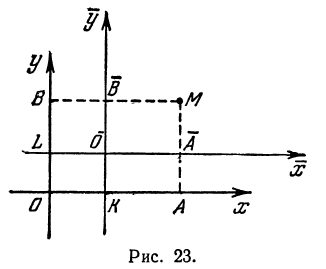
При параллельном сдвиге осей координат старая координата точки равна новой координате той же точки плюс координата нового начала в старой системе.
Исследование функции
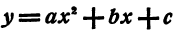
Функция, определенная уравнением

называется квадратичной функцией. Функция 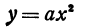 рассмотренная выше, является частным случаем квадратичной функции. Поставим перед собой цель—выяснить, как изменится уравнение (1), если перейти к новым координатам. Возьмем новые оси координат так, чтобы они были параллельны старым, т. е. ось
рассмотренная выше, является частным случаем квадратичной функции. Поставим перед собой цель—выяснить, как изменится уравнение (1), если перейти к новым координатам. Возьмем новые оси координат так, чтобы они были параллельны старым, т. е. ось  будет параллельна оси Ох,
будет параллельна оси Ох,
а ось  — оси Оу. Масштаб и направление осей такие же, как и у старых. Пусть координаты нового начала в старой системе будут х0 и у0. Подставим в уравнение (5) вместо х и у их выражения через новые координаты:
— оси Оу. Масштаб и направление осей такие же, как и у старых. Пусть координаты нового начала в старой системе будут х0 и у0. Подставим в уравнение (5) вместо х и у их выражения через новые координаты: 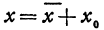 ,
, 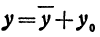 . Получим
. Получим
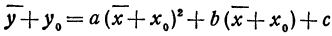
Разрешив это уравнение относительно 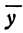 , будем иметь
, будем иметь
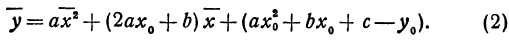
Координаты нового начала находятся в нашем распоряжении, поэтому их можно выбрать так, чтобы выполнялись условия
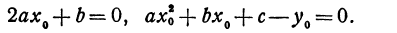
В этих уравнениях два неизвестных: х0 и у0. Найдем их:
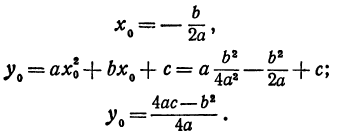
Если взять новое начало в точке
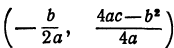
то в уравнении (2) скобки
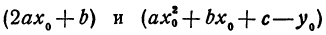
сделаются равными нулю, т. е. уравнение (2) примет вид

Полученное уравнение имеет вид, рассмотренный выше. Таким образом, уравнение 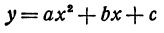 относительно новой системы координат определяет ту же параболу, что и уравнение
относительно новой системы координат определяет ту же параболу, что и уравнение 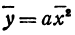 .Приходим к выводу:
.Приходим к выводу:
Уравнение 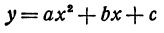 определяет параболу, вершина которой находится в точке
определяет параболу, вершина которой находится в точке 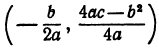 и ветви которой направлены вверх, если а > 0, и вниз, если а < 0. Тот же вывод можно высказать по-другому: График квадратической функции есть парабола с вершиной в точке
и ветви которой направлены вверх, если а > 0, и вниз, если а < 0. Тот же вывод можно высказать по-другому: График квадратической функции есть парабола с вершиной в точке 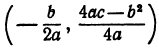 ветви которой направлены вверх, если а > 0, и вниз, если а < 0.
ветви которой направлены вверх, если а > 0, и вниз, если а < 0.
Пример:
Выяснить вид и расположение параболы, заданной уравнением

Переносим начало координат в точку (х0, у0), координаты которой пока неизвестны. Старые координаты я, у выражаются через новые  ,
, 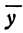 по формулам
по формулам
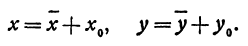
Подставляя эти выражения в уравнение (4), получим:
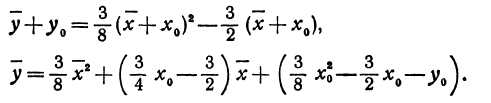
Выберем координаты нового начала так, чтобы соблюдались равенства
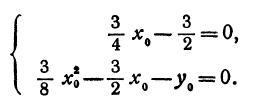
Решая полученную систему уравнений, будем иметь:
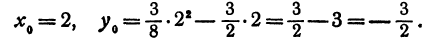
Следовательно, перенося начало координат в точку 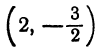 , преобразуем уравнение (4) в новое уравнение, которое имеет вид
, преобразуем уравнение (4) в новое уравнение, которое имеет вид

Следовательно, уравнение (4) определяет параболу, имеющу вершину в точке 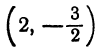 ; ветви параболы направлены вверх (рис. 24).
; ветви параболы направлены вверх (рис. 24).
Приведем пример применения квадратичной функции в механике.
Задача:
Найти траекторию тела, брошенного под углом к горизонту. Угол бросания а, скорость бросания . Сопротивлением воздуха пренебрегаем.
. Сопротивлением воздуха пренебрегаем.
Решение:
Выберем оси координат так: ось Оу—вертикальная прямая, проведенная в точке бросания , ось Ох— горизонтальная прямая, начало координат—точка бросания (рис. 25).
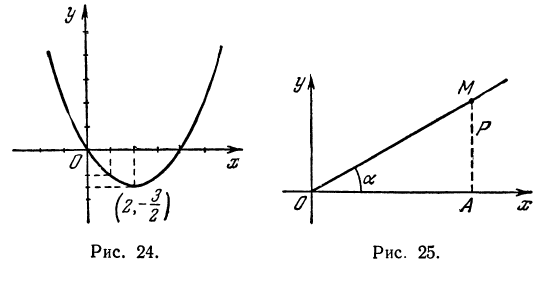
Если бы не действовала сила притяжения Земли, то тело, брошенное под углом к горизонту, по инерции двигалось бы по прямой ОМ. За t сек оно прошло бы расстояние 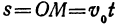 и, стало быть, находилось бы в точке М. Но под действием силы притяжения Земли это тело, как свободно падающее, за t сек пройдет вниз путь
и, стало быть, находилось бы в точке М. Но под действием силы притяжения Земли это тело, как свободно падающее, за t сек пройдет вниз путь  следовательно, тело фактически будет в точке Р. Вычислим координаты точки Р:
следовательно, тело фактически будет в точке Р. Вычислим координаты точки Р:
Найдем уравнение, связывающее х с у. Для этого из уравнения (*) найдем t и подставим это выражение в уравнение (**):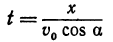
и, следовательно,
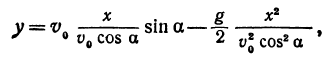
или
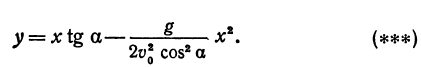
Мы получили уравнение траектории тела. Как мы видим, это есть квадратичная функция рассмотренного вида, следовательно, тело, брошенное под углом к горизонту, движется в безвоздушном пространстве по параболе, расположенной вершиной вверх, поскольку коэффициент при 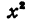 отрицателен.
отрицателен.
Какова наибольшая высота подъема тела над Землей? Чтобы ответить на этот вопрос, нужно найти вершину параболы. Как было выведено, вершина параболы имеет координаты
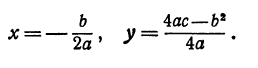
В нашей задаче
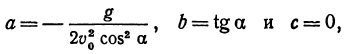
этому координаты вершины равны
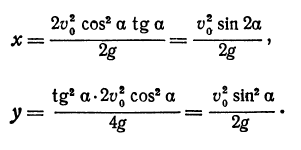
Найдем теперь дальность полета тела, т. е. абсциссу точки падения. Для этого приравняем в уравнении (***) у нулю, получим уравнение
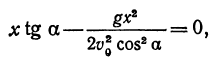
решая которое найдем два значения
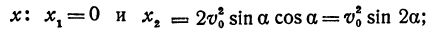
первое из них дает точку бросания, а второе — искомую абсциссу точки падения.
Все эти рассуждения относятся к безвоздушному пространству; в воздухе и высота и дальность будут значительно меньше.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

