Оглавление:
Первообразная и неопределенный интеграл:
Операция нахождения производной от функции называется дифференцированием. Обратная дифференцированию операция — отыскание функции по ее производной — называется интегрированием. Функция 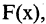 производная которой равна некоторой функции
производная которой равна некоторой функции 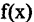 , т.е.
, т.е. 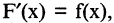 называется первообразной для
называется первообразной для 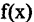 . Так, например, если
. Так, например, если 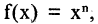 то ее первообразная есть
то ее первообразная есть
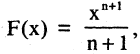 если же
если же 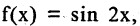 то ее первообразная
то ее первообразная 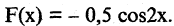 Поскольку производная любой постоянной величины равна нулю, то
Поскольку производная любой постоянной величины равна нулю, то 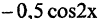 является первообразной не только для
является первообразной не только для 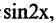 но и для
но и для 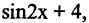 и для
и для 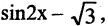 и вообще для любой функции вида
и вообще для любой функции вида 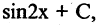 т.е. первообразные одной и той же функции отличаются на постоянную величину. Обобщая вышеизложенное, можно сказать, что функция
т.е. первообразные одной и той же функции отличаются на постоянную величину. Обобщая вышеизложенное, можно сказать, что функция 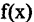 имеет бесконечное множество первообразных вида
имеет бесконечное множество первообразных вида 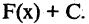
Множество всех первообразных для функции 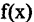 называется неопределенным интегралом от этой функции и обозначается так
называется неопределенным интегралом от этой функции и обозначается так

где 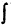 — знак интеграла, читается «интеграл»,
— знак интеграла, читается «интеграл», 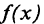 — подынтегральная функция от переменной интегрирования
— подынтегральная функция от переменной интегрирования 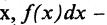 подынтегральное выражение. С — постоянная интегрирования.
подынтегральное выражение. С — постоянная интегрирования.
Основные свойства неопределенного интеграла
1.Из определения интеграла следует, что
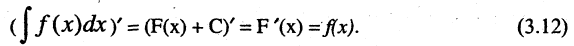
Так как 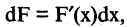 то
то
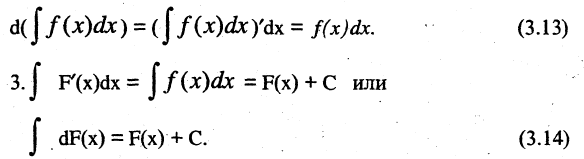
Формулы 3.12-3.14 наглядно иллюстрируют то обстоятельство, что операции дифференцирования и интегрирования взаимно обратны с точностью до постоянной.
4.Постоянный множитель можно выносить за знак неопределенного интеграла.
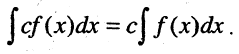
5.Неопределенный интеграл от суммы функций равен сумме неопределенных интегралов от этих функций.
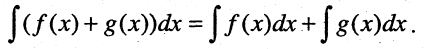
Замечание:
Если каждый из суммируемых неопределенных интегралов содержит свою постоянную интегрирования, то для всей суммы записывается одна постоянная интегрирования.
Как было сказано, операции дифференцирования и интегрирования обратны, поэтому таблица неопределенных интегралов является следствием таблицы производных. Если интеграл не является табличным, то при помощи специальных методов он должен быть сведен к табличному. Методы, позволяющие преобразовать интегралы к табличным, называются методами интегрирования.
Таблица основных интегралов

Пример:
Найти 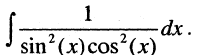
Решение:
Запишем стоящую в числителе единицу в тригонометрическом виде 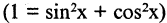 и, разделив почленно числитель на знаменатель, получим табличные интегралы:
и, разделив почленно числитель на знаменатель, получим табличные интегралы:
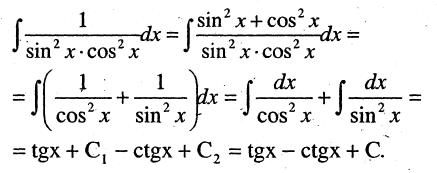
Методы интегрирования
Перечислим основные методы интегрирования.
Метод интегрирования по частям
Пусть на некотором промежутке существуют производные функций 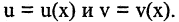
По правилу дифференцирования произведения, имеем
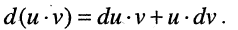
Проинтегрируем это равенство, учитывая, что
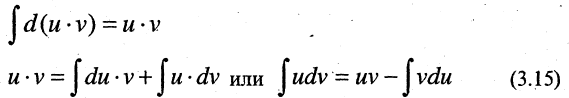
Эта формула носит название формулы интегрирования по частям. Ее применение полезно в тех случаях, когда подынтегральное выражение можно представить в виде произведения двух функций 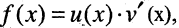 а выражение
а выражение 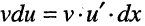 для вычисления интеграла проще, чем подынтегральное выражение
для вычисления интеграла проще, чем подынтегральное выражение 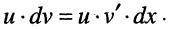
Пример:
Найти 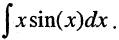 Так как производная от х равна 1, то возьмем
Так как производная от х равна 1, то возьмем 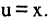 Используем схему записи в виде, удобном для метода интегрирования по частям:
Используем схему записи в виде, удобном для метода интегрирования по частям:
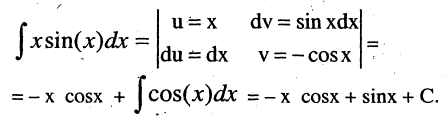
Метод замены переменной
Добиться упрощения подынтегрального выражения можно при помощи метода замены переменной интегрирования. Суть этого метода заключается в замене переменной интегрирования х на некоторую функцию u(t) с тем, чтобы преобразовать исходный интеграл к более простому виду.
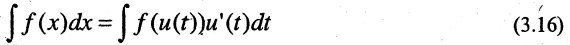
Формула (3.16) называется формулой замены переменной под знаком неопределенного интеграла. Важные частные случаи:
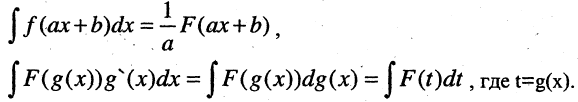
Алгоритм метода замены переменной следующий. Вначале необходимо найти замену переменной интегрирования 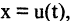 записать интеграл с новой переменной интегрирования t, вычислить его, а затем вновь вернуться к исходной переменной интегрирования.
записать интеграл с новой переменной интегрирования t, вычислить его, а затем вновь вернуться к исходной переменной интегрирования.
Пример:
Найти 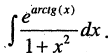 Особенностью данного интеграла является то обстоятельство, что его подынтегральное выражение содержит множитель
Особенностью данного интеграла является то обстоятельство, что его подынтегральное выражение содержит множитель 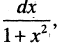 который является дифференциалом функции
который является дифференциалом функции 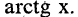 Поэтому в данном интеграле целесообразно ввести замену переменной:
Поэтому в данном интеграле целесообразно ввести замену переменной: 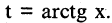 Отсюда
Отсюда 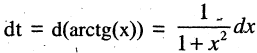 Подставляя в исходный интеграл, имеем
Подставляя в исходный интеграл, имеем
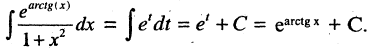
Пример:
Найти 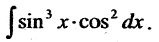
Решение. Здесь уместна замена 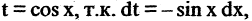 и
и 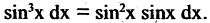 Поэтому
Поэтому
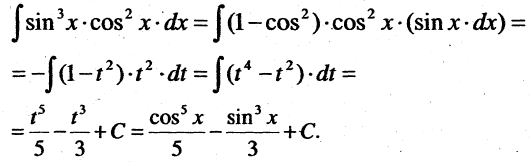
Первообразная и неопределенный интеграл





Смотрите также:
| Частные производные высших порядков. | Табличные интегралы. |
| Дифференциалы высших порядков. | Интегрирование подстановкой (замена переменной). |
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Линейная функция
- Выпуклые множества точек
- Система координат

