Точка 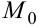 называется точкой максимума функции
называется точкой максимума функции 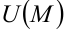 , если значение функции в этой точке больше, чем её значение в любой другой точке некоторой (хотя бы малой) окрестности точки
, если значение функции в этой точке больше, чем её значение в любой другой точке некоторой (хотя бы малой) окрестности точки 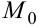 . Аналогично (с заменой «больше» на «меньше») определяется точка минимума функции.
. Аналогично (с заменой «больше» на «меньше») определяется точка минимума функции.
Точки минимума и максимума объединяются под общим названием точки экстремума.
Для функции двух переменных точка 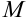 имеет две координаты
имеет две координаты 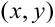 для функции трёх переменных — три координаты
для функции трёх переменных — три координаты 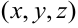 . При этом окрестностью точки
. При этом окрестностью точки 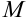
 является открытый шар с центром в этой точке.
является открытый шар с центром в этой точке.
Поиск критических точек, т.е. точек в которых может быть экстремум функции 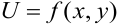 , производится при помощи необходимого условия экстремума:
, производится при помощи необходимого условия экстремума:

Решение системы (8.12) определяет координаты критических точек 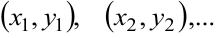
Однако необходимого условия мало для существования точек экстремума.
Нужно провести исследование критических точек с использованием достаточных условий экстремума.
Для функции двух переменных 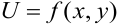 введём обозначения для вторых частных производных в критической точке
введём обозначения для вторых частных производных в критической точке 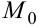
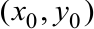 :
:
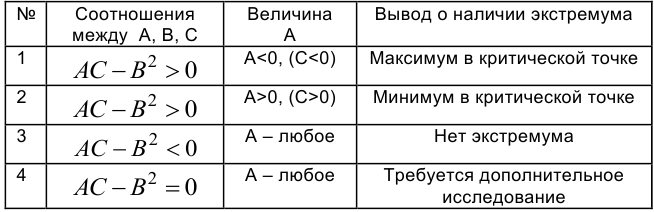
Достаточные условия приводим в таблице 4.
Таблица 4 — Достаточные условия экстремума функции двух переменных
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Производная по направлению |
| Градиент и его свойства |
| Основные определения о дифференциальных уравнениях |
| Дифференциальные уравнения первого порядка |
