Оглавление:
Задание: Нахождение радиуса и интервала сходимости степенного ряда.
Цель: формирование умения находить радиус и интервал сходимости степенных рядов.
Задание для самостоятельной внеаудиторной работы:
41.1. Выучите определение степенного ряда. Сформулируйте определение радиуса сходимости степенного ряда. Выясните, какова техника его нахождения.
41.2. Проанализируйте, в каких случаях для вычисления радиуса сходимости степенного ряда 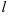 удобно искать по формуле
удобно искать по формуле 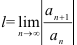 , а в каких — по формуле —
, а в каких — по формуле — 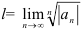 . Внимательно изучите примеры, позволяющие находить радиус сходимости степенного ряда.
. Внимательно изучите примеры, позволяющие находить радиус сходимости степенного ряда.
41.3. Найдите радиус сходимости степенного ряда:
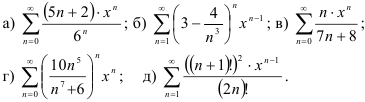

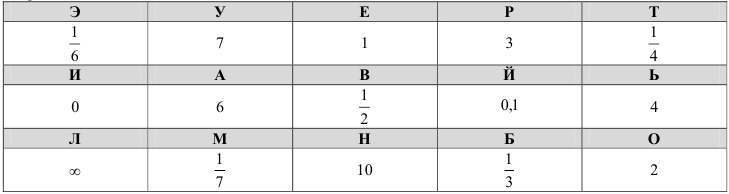
Выполнив задание 41.3. и заменив получившиеся ответы буквами из таблицы. Вы откроете фамилию математика — автора теоремы:
Если степенной ряд 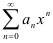 сходится в точке
сходится в точке 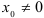 , то он сходится, и притом абсолютно, для всех
, то он сходится, и притом абсолютно, для всех 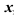 , удовлетворяющих неравенству:
, удовлетворяющих неравенству: 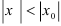 .
.
Его работы в теории рядов фундаментальны. Огромное число понятий и теорем в различных областях математики носит его имя. За свою короткую жизнь этот учёный сделал важнейшее для науки открытие: доказал, что алгебраические уравнения степени выше четвёртой в общем случае неразрешимы в радикалах.
На его родине знаменитому математику установлен необычный памятник. По круто поднимающейся гранитной глыбе молодой человек с одухотворённым лицом шагает ввысь, переступая через два отвратительных чудовища. Что они символизируют? Одни математики, шутя, говорят, что они изображают уравнения пятой степени и эллиптические функции, побеждённые учёным. Другие утверждают, что скульптор воплотил в образе чудовищ социальную несправедливость. Именно с ней всю жизнь боролся учёный. Только в этой трактовке автор памятника погрешил против истины: не математик победил эти чудовища, а они погубили его…
Фамилия математика — автора теоремы:

Карта ответов:
41.4. Выучите определение интервала сходимости степенного ряда. Выясните, какова техника его нахождения.
41.5. Найдите интервал сходимости степенного ряда:
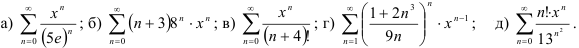
Методические указания по выполнению работы:
Для успешного решения задач необходимо знание следующего теоретического материала:
Функциональный ряд вида  , членами которого являются степенные функции аргумента
, членами которого являются степенные функции аргумента 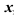 , называется степенным (
, называется степенным (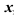 — действительная переменная, действительные числа
— действительная переменная, действительные числа  — коэффициенты степенного ряда).
— коэффициенты степенного ряда).
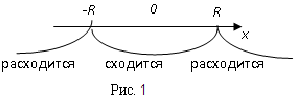
Радиусом сходимости 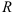 степенного ряда
степенного ряда 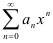 называется неотрицательное действительное число или
называется неотрицательное действительное число или 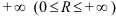 , удовлетворяющее условиям: при всех
, удовлетворяющее условиям: при всех 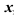 , для которых
, для которых 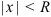 степенной ряд
степенной ряд 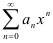 сходится; при всех
сходится; при всех 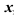 , для которых
, для которых 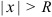 , степенной ряд
, степенной ряд 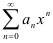 расходится.
расходится.
Если степенной ряд 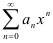 сходится лишь в одной точке
сходится лишь в одной точке 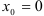 , то его радиус сходимости равен 0:
, то его радиус сходимости равен 0: 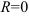 .
.
Если степенной ряд 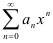 сходится при всех действительных значениях переменной
сходится при всех действительных значениях переменной 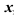 (во всех точках числовой оси), то его радиус сходимости равен
(во всех точках числовой оси), то его радиус сходимости равен 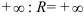 .
.
У любого степенного ряда есть радиус сходимости, найти который позволяет следующая теорема.
Теорема. Если для степенного ряда 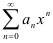 существуют конечные или бесконечные пределы
существуют конечные или бесконечные пределы 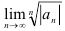 или
или 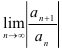 , равные
, равные 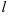 , то радиус сходимости степенного ряда находится по формуле:
, то радиус сходимости степенного ряда находится по формуле: 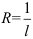 .
.
Заметим, что находить 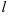 можно, фактически осуществляя ту же последовательность действий, что и в алгоритмах, предназначенных для исследования сходимости положительных рядов по признакам Даламбера и Коши. При этом роль общего члена положительного ряда будет играть коэффициент
можно, фактически осуществляя ту же последовательность действий, что и в алгоритмах, предназначенных для исследования сходимости положительных рядов по признакам Даламбера и Коши. При этом роль общего члена положительного ряда будет играть коэффициент 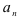 степенного ряда.
степенного ряда.
Рассмотрим примеры нахождения радиуса сходимости степенного ряда.
Пример 1.
Найдите радиус сходимости степенного ряда 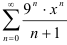 .
.
Решение:
Радиус сходимости степенного ряда 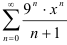 будем искать по формуле:
будем искать по формуле: 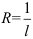 . Поскольку коэффициент степенного ряда
. Поскольку коэффициент степенного ряда 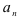 содержит выражение
содержит выражение 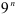 , то для нахождения
, то для нахождения 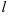 применим формулу:
применим формулу: 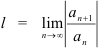 , аналогичную формуле признака Даламбера. Фактически
, аналогичную формуле признака Даламбера. Фактически
воспользуемся соответствующим алгоритмом. Для этого:
- найдём коэффициент
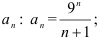
- найдём коэффициент
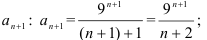
- найдём отношение коэффициентов
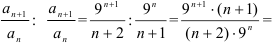
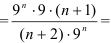
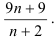
Таким образом, получим
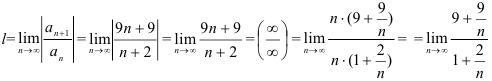
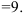
Следовательно, так как 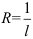 , а
, а 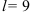 , то
, то 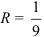 .
.
Ответ: 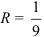 .
.
Если для степенного ряда 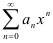
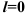 , то его радиус сходимости
, то его радиус сходимости 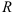 равен
равен 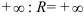 .
.
Если для степенного ряда 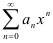
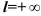 , то его радиус сходимости
, то его радиус сходимости 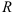 равен 0:
равен 0: 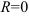 .
.
Пример 2.
Найдите радиус сходимости степенного ряда 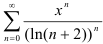 .
.
Решение:
Радиус сходимости степенного ряда 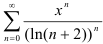 будем искать по формуле:
будем искать по формуле: 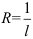 . Поскольку коэффициент степенного ряда
. Поскольку коэффициент степенного ряда 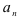 представляет собой
представляет собой 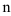 -ую степень выражения
-ую степень выражения 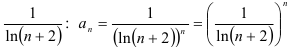 , то для нахождения
, то для нахождения 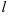 применим формулу:
применим формулу: 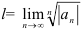 , аналогичную формуле признака Коши. Фактически воспользуемся соответствующим алгоритмом. Для этого:
, аналогичную формуле признака Коши. Фактически воспользуемся соответствующим алгоритмом. Для этого:
- найдём коэффициент
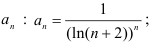
- найдем
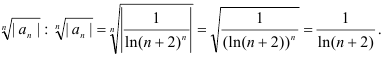
Таким образом, получим 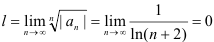 .
.
Следовательно, если 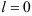 , то
, то 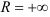 .
.
Ответ: 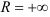 .
.
Если 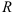 — радиус сходимости степенного ряда
— радиус сходимости степенного ряда 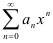 , то множество точек
, то множество точек 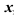 , удовлетворяющих неравенству
, удовлетворяющих неравенству 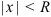 , называется интервалом сходимости I степенного ряда. Значит, если
, называется интервалом сходимости I степенного ряда. Значит, если 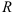 — радиус сходимости степенного ряда
— радиус сходимости степенного ряда 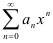 , то его интервал сходимости
, то его интервал сходимости
находится следующим образом: 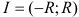 .
.
Пример 3.
Найдите интервал сходимости степенного ряда .
.
Решение:
Интервал сходимости степенного ряда определяется формулой: 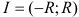 . Выясним, чему равен радиус сходимости данного степенного ряда. Искать его будем по соотношению:
. Выясним, чему равен радиус сходимости данного степенного ряда. Искать его будем по соотношению: 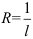 . Для нахождения
. Для нахождения 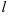 применим формулу:
применим формулу: 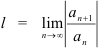 , аналогичную формуле признака Даламбера. Фактически воспользуемся соответствующим алгоритмом. Для этого:
, аналогичную формуле признака Даламбера. Фактически воспользуемся соответствующим алгоритмом. Для этого:
- найдём коэффициент
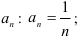
- найдём коэффициент
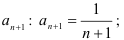
- найдём отношение коэффициентов
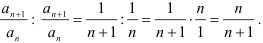
Таким образом, получим
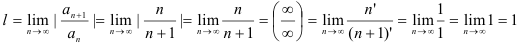
(при раскрытии неопределённости 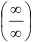 использовали правило Лопиталя). Следовательно, так как
использовали правило Лопиталя). Следовательно, так как 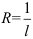 , а
, а 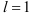 , то
, то 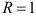 .
.
Применяя формулу для нахождения интервала сходимости степенного ряда: 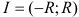 , получим:
, получим: 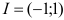 .
.
Ответ: 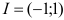 .
.
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:

