Оглавление:
Задание: Исследование сходимости числовых положительных рядов.
Цель: формирование умения применять достаточные признаки (сравнения, Даламбера, радикальный и интегральный Коши) при исследовании рядов на сходимость.
Задание для самостоятельной внеаудиторной работы:
39.1. Выучите определение положительного (знакоположительного) ряда. Сформулируйте признак сравнения. Выясните, какова техника его применения для исследования сходимости положительных рядов. Запомните ряды, традиционно использующиеся в качестве «эталонных» для исследования сходимости ряда по признаку сравнения.
39.2. С помощью признака сравнения исследуйте на сходимость положительные ряды:
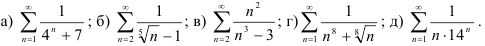
39.3. Сформулируйте признак Даламбера. Постарайтесь освоить алгоритм, позволяющий исследовать сходимость положительного ряда по признаку Даламбера. Изучите пример исследования сходимости ряда 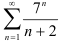 по этому признаку.
по этому признаку.
39.4. С помощью признака Даламбера исследуйте на сходимость положительные ряды:
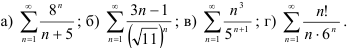
39.5. Сформулируйте признак Коши (радикальный). Постарайтесь освоить алгоритм, позволяющий исследовать сходимость положительного ряда по признаку Коши. Изучите пример исследования сходимости ряда 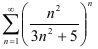 по этому признаку.
по этому признаку.
39.6. С помощью признака Коши исследуйте на сходимость положительные ряды:
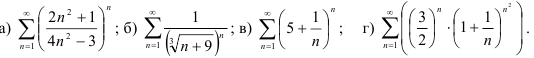
39.7. Выясните, в чём заключается интегральный признак Коши, и как он применяется для исследования сходимости положительных рядов.
39.8. С помощью интегрального признака Коши исследуйте на сходимость положительные ряды:
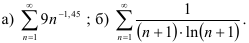
39.9. Проанализируйте, в каких случаях исследовать положительный ряд на сходимость целесообразно с помощью признака сравнения, в каких — с помощью признака Даламбера, а в каких — с помощью признаков Коши.
39.10. Исследуйте на сходимость положительные ряды:
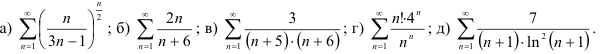
Методические указания по выполнению работы:
Для успешного решения задач необходимо знание следующего теоретического материала: Числовой ряд с неотрицательными членами называется положительным (знакоположительным).
Признак сравнения позволяет исследовать положительный ряд на сходимость путем сравнения его с другим («эталонным») рядом, о котором известно, сходится он или нет.
Признак сравнения: Пусть даны два положительных ряда 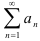 и
и 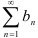 . Если, начиная с некоторого номера, выполняется неравенство
. Если, начиная с некоторого номера, выполняется неравенство 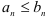 , то
, то
- из сходимости ряда
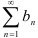 следует сходимость ряда
следует сходимость ряда 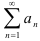 ;
; - из расходимости ряда
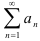 следует расходимость ряда
следует расходимость ряда 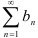 .
.
Другими словами:
- если общий член исследуемого ряда меньше общего члена сходящегося ряда, то исследуемый ряд сходится;
- если общий член исследуемого ряда больше общего члена расходящегося ряда, то исследуемый ряд расходится.
В качестве «эталонных» обычно используют следующие ряды:
1. 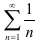 — расходящийся гармонический ряд;
— расходящийся гармонический ряд;
2. 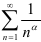 , если
, если 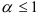 — расходящийся обобщённый гармонический ряд,
— расходящийся обобщённый гармонический ряд,
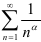 , если
, если 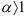 — сходящийся обобщённый гармонический ряд;
— сходящийся обобщённый гармонический ряд;
3. 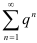 , если
, если 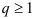 — расходящийся ряд геометрической прогрессии,
— расходящийся ряд геометрической прогрессии,
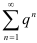 , если
, если 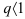 — сходящийся ряд геометрической прогрессии.
— сходящийся ряд геометрической прогрессии.
Рассмотрим примеры использования признака сравнения для исследования сходимости положительных рядов.
Пример 1.
Исследуйте ряд 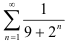 на сходимость, применяя признак сравнения.
на сходимость, применяя признак сравнения.
Решение:
Сравним данный ряд с «эталонным» рядом геометрической прогрессии 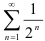
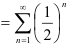 , который сходится
, который сходится 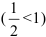 . Имеем:
. Имеем: 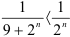 . Таким образом, общий член нашего ряда меньше общего члена сходящегося ряда. Следовательно, по признаку сравнения, ряд
. Таким образом, общий член нашего ряда меньше общего члена сходящегося ряда. Следовательно, по признаку сравнения, ряд 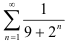 сходится.
сходится.
Ответ: 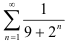 сходится.
сходится.
Пример 2.
Исследуйте ряд 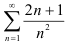 на сходимость, применяя признак сравнения.
на сходимость, применяя признак сравнения.
Решение:
Рассмотрим ряд 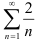 . Поскольку он получается из расходящегося гармонического ряда
. Поскольку он получается из расходящегося гармонического ряда 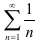 умножением на 2, то, по свойству числовых рядов (свойство 2), он расходится. Сравним исследуемый ряд с рядом
умножением на 2, то, по свойству числовых рядов (свойство 2), он расходится. Сравним исследуемый ряд с рядом 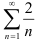 . Имеем:
. Имеем: 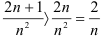 , т.е.
, т.е. 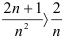 . Таким образом, общий член исследуемого ряда больше общего члена расходящегося ряда. Следовательно, по признаку сравнения, ряд
. Таким образом, общий член исследуемого ряда больше общего члена расходящегося ряда. Следовательно, по признаку сравнения, ряд 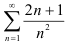 расходится.
расходится.
Ответ: 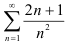 расходится.
расходится.
В отличие от признака сравнения, где многое зависит от догадки и запаса «эталонных» рядов, признак Даламбера часто позволяет исследовать сходимость ряда, проделав лишь некоторые операции над ним.
Признак Даламбера: Пусть дан положительный числовой ряд 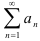 и существует конечный или бесконечный предел
и существует конечный или бесконечный предел 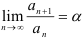 . Тогда:
. Тогда:
- если
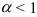 , то ряд
, то ряд 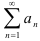 сходится;
сходится; - если
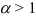 , то ряд
, то ряд 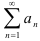 расходится;
расходится; - если
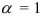 , то признак не применяется (вопрос о сходимости ряда остается открытым).
, то признак не применяется (вопрос о сходимости ряда остается открытым).
Исследовать ряд 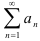 на сходимость по признаку Даламбера удобно по следующему алгоритму:
на сходимость по признаку Даламбера удобно по следующему алгоритму:
1) найти 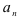 ;
;
2) найти 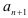 ;
;
3) найти 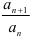 ;
;
4) найти предел отношения на бесконечности 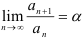 и проанализировать полученное значение:
и проанализировать полученное значение:
- если
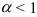 , то ряд
, то ряд 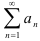 сходится;
сходится; - если
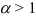 , то ряд
, то ряд 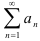 расходится;
расходится; - если
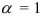 , то признак Даламбера ответа не дает (требуется дополнительное исследование).
, то признак Даламбера ответа не дает (требуется дополнительное исследование).
Рассмотрим пример использования признака Даламбера для исследования сходимости положительных рядов.
Пример 3.
Исследуйте ряд 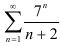 на сходимость, применяя признак Даламбера.
на сходимость, применяя признак Даламбера.
Решение:
Для исследования сходимости ряда по признаку Даламбера воспользуемся алгоритмом:
1) найдём 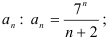
2) найдём 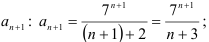
3) найдём 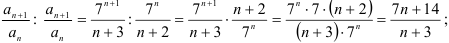
4) найдём 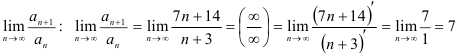 (при раскрытии неопределенности
(при раскрытии неопределенности 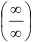 использовали правило Лопиталя). Получили, что
использовали правило Лопиталя). Получили, что 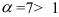 . Значит, по признаку Даламбера ряд
. Значит, по признаку Даламбера ряд 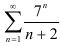 расходится.
расходится.
Ответ: 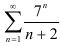 расходится.
расходится.
Заметим, что признак Даламбера целесообразно применять в том случае, когда общий член ряда содержит выражение вида 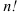 или
или 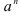 .
.
Иногда для исследования сходимости положительного ряда удобно использовать радикальный признак Коши, во многом схожий с признаком Даламбера.
Признак Коши (радикальный): Пусть дан положительный числовой ряд 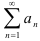 , и существует конечный или бесконечный предел
, и существует конечный или бесконечный предел 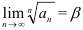 . Тогда:
. Тогда:
- если
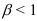 , то ряд
, то ряд 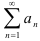 сходится;
сходится; - если
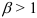 , то ряд
, то ряд 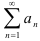 расходится;
расходится; - если
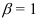 , признак не применяется (вопрос о сходимости ряда остается открытым).
, признак не применяется (вопрос о сходимости ряда остается открытым).
Исследовать ряд 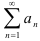 на сходимость по признаку Коши удобно по следующему алгоритму:
на сходимость по признаку Коши удобно по следующему алгоритму:
1) найти 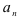 ;
;
2) найти 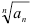 ;
;
3) найти 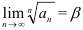 и проанализировать полученное значение:
и проанализировать полученное значение:
- если
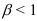 , то ряд
, то ряд 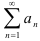 сходится;
сходится; - если
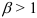 , то ряд
, то ряд 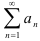 расходится;
расходится; - если
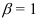 , то признак Коши ответа не дает (требуется дополнительное исследование).
, то признак Коши ответа не дает (требуется дополнительное исследование).
Пример 4.
Исследуйте ряд 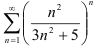 на сходимость, применяя признак Коши.
на сходимость, применяя признак Коши.
Решение:
Для исследования сходимости ряда по признаку Коши воспользуемся алгоритмом:
1) найдём 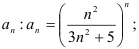
2) найдём 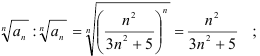
3) найдём 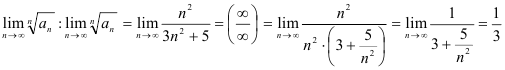 . Получили, что
. Получили, что 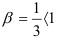 . Значит, по признаку Коши ряд
. Значит, по признаку Коши ряд 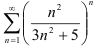 сходится.
сходится.
Ответ: 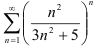 сходится.
сходится.
Заметим, что признак Коши целесообразно применять в том случае, когда общий член ряда представляет собой 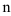 -ую степень выражения.
-ую степень выражения.
В некоторых ситуациях, когда ни один из признаков сравнения, Даламбера, Коши не дает ответ о сходимости положительного ряда, исследовать ряд на сходимость позволяет интегральный признак Коши.
Интегральный признак Коши: Если члены положительного ряда 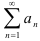 могут быть представлены как числовые значения некоторой непрерывной монотонно убывающей на промежутке
могут быть представлены как числовые значения некоторой непрерывной монотонно убывающей на промежутке 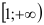 функции
функции 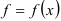 так, что
так, что 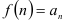 , то данный ряд
, то данный ряд 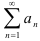 и несобственный интеграл
и несобственный интеграл 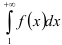 одновременно сходятся или расходятся.
одновременно сходятся или расходятся.
Пример 5.
Исследуйте ряд 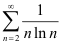 на сходимость, применяя интегральный признак Коши.
на сходимость, применяя интегральный признак Коши.
Решение:
Рассмотрим функцию 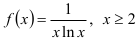 . Эта функция непрерывна, монотонно убывает на
. Эта функция непрерывна, монотонно убывает на 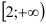 , и
, и 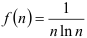 , следовательно, можно применить интегральный признак Коши.
, следовательно, можно применить интегральный признак Коши.
Выясним, будет ли несобственный интеграл 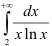 сходиться или расходиться.
сходиться или расходиться.
Имеем: 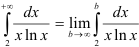 .
.
Отдельно найдём неопределённый интеграл 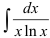 методом замены переменной:
методом замены переменной:
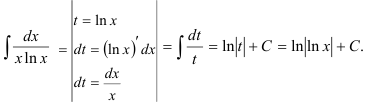
Найдем предел: 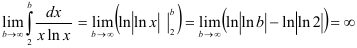 .
.
Таким образом, получили 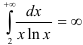 . Следовательно, несобственный интеграл
. Следовательно, несобственный интеграл 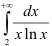 расходится. Значит, в силу интегрального признака Коши, ряд
расходится. Значит, в силу интегрального признака Коши, ряд 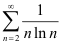 также будет расходиться.
также будет расходиться.
Ответ: 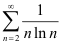 расходится.
расходится.
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:

