Число е в математике и его применение с примерами решения

Оглавление:

Возникновение числа е:

Рассмотрим выражение

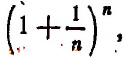
в котором n — натуральное число.

Изучение этого выражения необходимо для решения очень многих крайне важных задач (см., например, следующий параграф и главу «Производная, дифференциал, интеграл и их простейшие применения»).

Если мы станем натуральное число n неограниченно увеличивать, то величина выражения

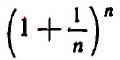
станет величиной переменной. Эта переменная не стремится к единице, как это может показаться на первый взгляд. Действительно, мы сейчас убедимся в том, что при возрастании натурального числа n значение выражения

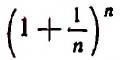
будет монотонно* возрастать, начиная со значения, равного двум. Например,

Последовательность 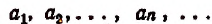называется возрастающей, если 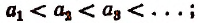неубывающей, если 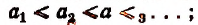убывающей, если 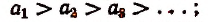невозрастающей, если 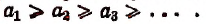Все такие последовательности называются монотонными.

Чтобы доказать, что переменная

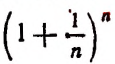
монотонно возрастает при возрастании n, применим формулу бинома Ньютона:

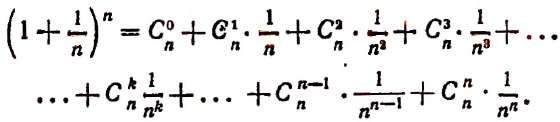
Перепишем эту формулу в следующем виде:

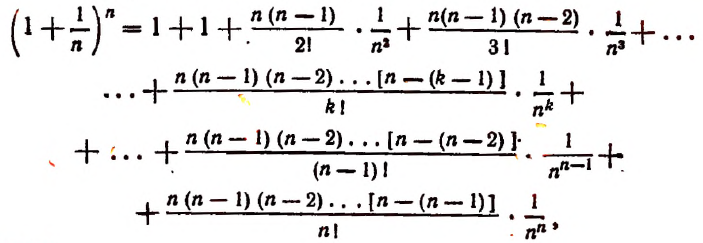
или так:

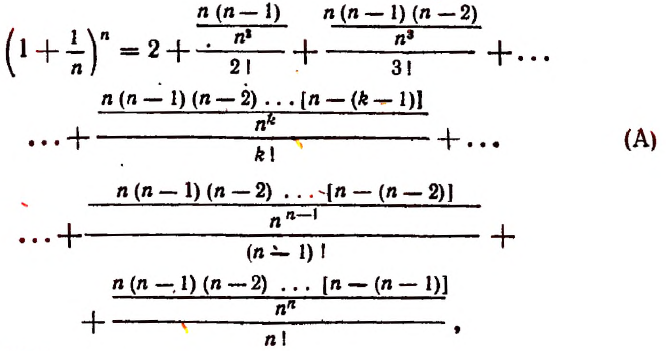
наконец, так:

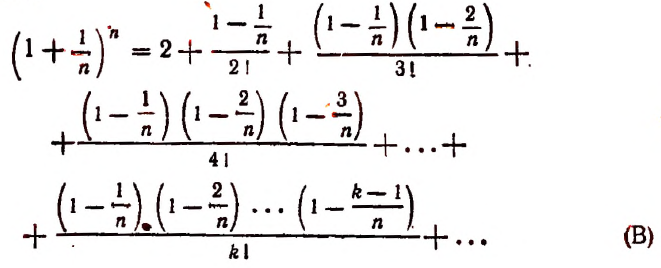
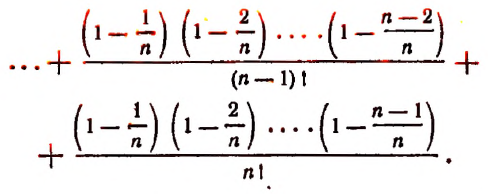
Все слагаемые в правой части этого равенства положительны.

При возрастании числа n правая часть этого равенства будет монотонно возрастать, так как будет возрастать число слагаемых и каждое слагаемое, начиная со второго.

Значит, доказано, что переменная 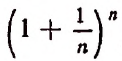будет монотонно возрастать при возрастании числа n.

Теперь докажем, что, несмотря на то что переменная 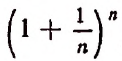монотонно возрастает, тем не менее она будет оставаться всегда меньшей, чем число 2,75.

Из формулы (В) видно, что

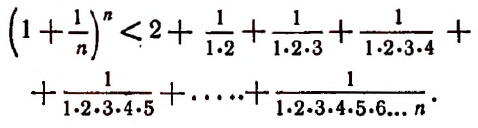
Тем более будет верным неравенство

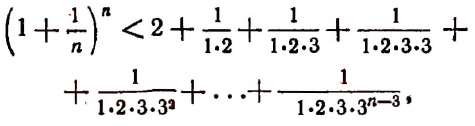
К сумме, написанной в квадратных скобках, применим формулу суммы членов конечной геометрической прогрессии. Тогда получим:

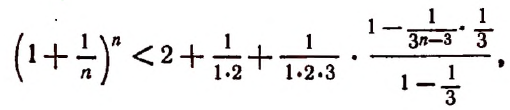
или

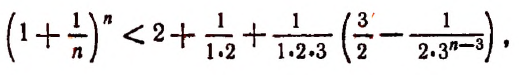
и тем более будет верным неравенство

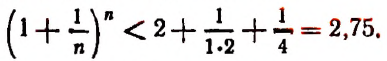
Кроме этого, из формулы (А) видно, что всегда

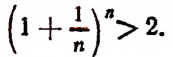
Теперь перейдем к самому важному выводу.

Мы доказали, что переменная 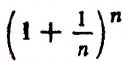монотонно возрастает при возрастании n и при этом всегда остается меньше, чем 2,75. По признаку Вейерштрасса (см. стр. 408) эта переменная имеет предел. Этим пределом будет определенное число, большее двух и не большее 2,75. Это число является иррациональным и обозначается, как это принято во всей математической литературе, буквой е. Значит, 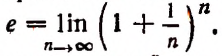Иррациональность числа е доказывается в курсах высшей математики.

Число е выражается бесконечной непериодической десятичной дробью. Первые цифры этой дроби идут в таком порядке:

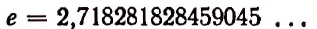
Напомним, что логарифмы по основанию е называются натуральными и обозначаются символом 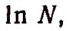так что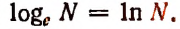

Применения числа е

Исходя из полученного равенства

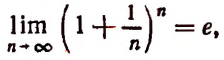
можно доказать, что

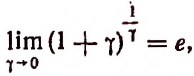
где 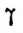— любая бесконечно малая величина, могущая принимать и положительные и отрицательные значения.

Последнее равенство можно сформулировать так:

Степень, основанием которой служит единица плюс бесконечно малое слагаемое 7, а показателем величина, обратная этому слагаемому, стремится к числу е, как к своему, пределу (доказательство опускается).

Обратим внимание на то, что основание этой степени стремится к единице, но, несмотря на это, сама степень не стремится к единице.

Рассмотрим пределы степеней, в которых основанием служит единица плюс бесконечно малое слагаемое, а показатель есть величина, обратная этому слагаемому.

Примеры:

1. Найти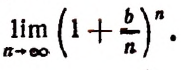

Решение:

Полагая 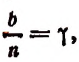получим 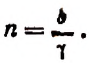При 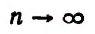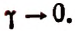Следовательно,

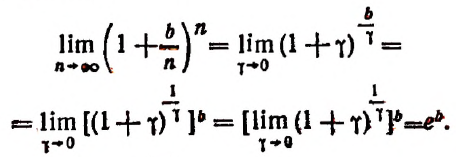
2. Найти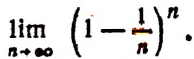

Полагая 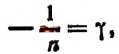получим 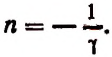Следовательно,

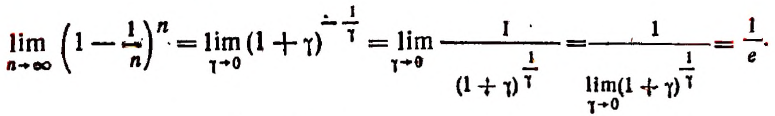
3. Найти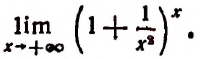

Полагая 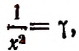получим 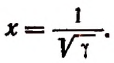Следовательно,

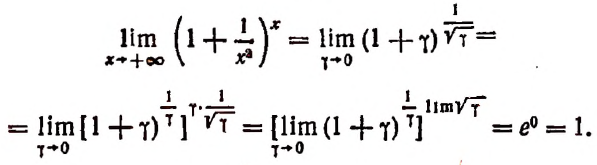
4. Найти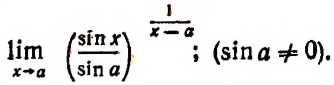

Представим 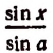в виде суммы, у которой первое слагаемое было бы единицей, а второе — величиной бесконечно малой. Это легко сделать.

Действительно,

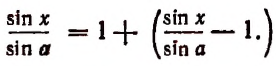
Здесь первое слагаемое есть единица, а второе, стоящее в скобках, есть величина бесконечно малая при

Таким образом, получим:

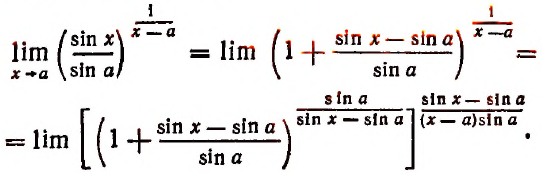
В квадратных скобках мы имеем степень, основанием которой является единица плюс бесконечно малое слагаемое, а показатель степени есть величина, обратная этому бесконечно малому слагаемому. Предел такой степени, как мы знаем, равен числу е.

Теперь найдем предел показателя степени, в который возводится выражение, стоящее в квадратных скобках:

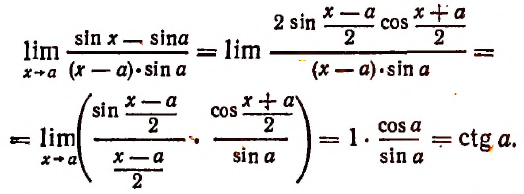
Следовательно,

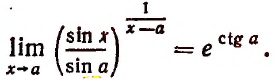
Задачи:

1. Пусть банк принял вклад в a руб. и обязался присоединять процентные деньги к вкладу через каждую 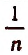часть года из расчета р годовых процентов. Спрашивается, в какую сумму обратится первоначальный вклад через t лет?

Одну n-ю часть года назовем установленным промежутком времени. Тогда один год будет содержать n, a t лет nt таких промежутков.

К концу первого промежутка времени вклад обратится в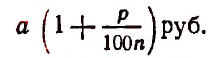

Действительно, за первый промежуток времени процентные деньги, подлежащие присоединению к вкладу, будут равны 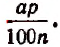Следовательно, вклад окажется равным 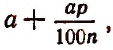т. е.

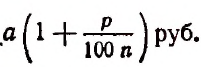
Обратим внимание на то, что для получения возросшей суммы за один промежуток времени достаточно вклад, имевшийся в начале промежутка, умножить на 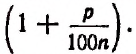Этот множитель называется множителем процентного наращения за промежуток времени, равный 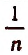части года.

Значит, чтобы получить возросшую сумму к концу второго промежутка времени, достаточно вклад, образовавшийся к началу второго промежутка времени, умножить на множитель процентного наращения и т. д.

Таким образом,

Итак, первоначальный вклад в а руб. обратится через t лет в

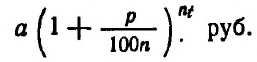
Теперь вообразим, что 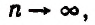т. е. что рост вклада происходит, как выражаются, органически. Тогда вклад в а руб. обратится через t лет в сумму А, определяемую равенством

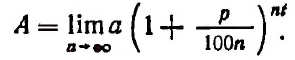
Полагая 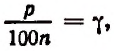найдем, что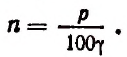

Отсюда

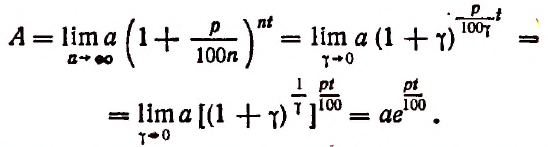
Итак, для органического роста вклада получилась следующая формула:

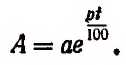
Например, при а = 1, р = 5 и f = 100

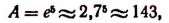
т. е. один рубль превращается через 100 лет приблизительно в 143 руб., если органический рост происходит по 5 годовых процентов.

2. Лесная делянка содержит в данный момент а куб. м древесины. Сколько окажется на этой делянке древесины через t лет, если органический рост древесины происходит по р годовых процентов.

Oтв. 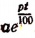куб. м.

3. Численность населения города увеличивается ежегодно на р% (по отношению к началу года). Через сколько лет численность населения удвоится?

Отв.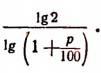

Формула Эйлера

Формула Эйлера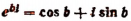

В заключение этой главы приведем еще одно важное соотношение, найденное гениальным Эйлером, устанавливающее связь между тригонометрическими функциями и показательной функцией. Было доказано, что

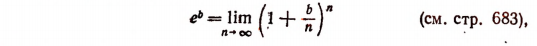
где b — любое действительное число.

Обобщая этот результат, примем по определению, что

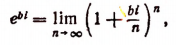
где b — любое действительное число, a i — мнимая единица. Теперь вычислим предел правой части последнего равенства.

Комплексное число 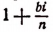представим в тригонометрической форме. Как известно (см. стр. 580),

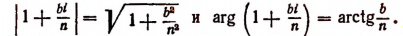
Поэтому

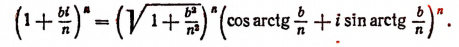
Пользуясь формулой Муавра, найдем, что

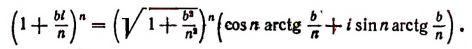
Теперь имеем:

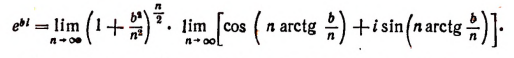
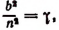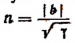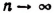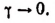Вычислим каждый из пределов, входящих в правую часть последней формулы. Обозначив получим, что и что при будет Следовательно,

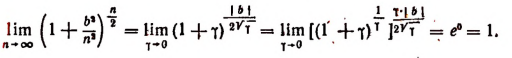
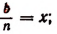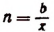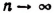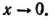Далее, обозначим тогда и при будет Следовательно,

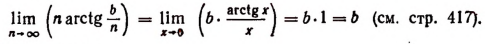
Теперь имеем:

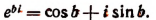
Эта формула и носит название формулы Эйлера.

Следствия из формулы Эйлера

1. Полагая в формуле Эйлера вместо b число 2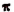, получим, что 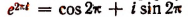или 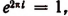т. е.установим связь между действительными числами е и и мнимой единицей I.

2. Полагая в формуле Эйлера вместо b число — b, получим, что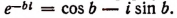

Из системы

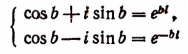
находим, что

3. Пользуясь формулой Эйлера, можно представить любое комплексное число еще в одной новой форме.

Действительно, обозначив модуль комплексного числа х + iy буквой r, а главное значение аргумента буквой 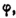получим:

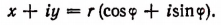
Но по формуле Эйлера

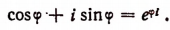
Поэтому получим:

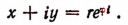
Выражение 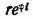называется показательной формой комплексного числа.

Справедливой будет и следующая запись:

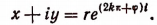
В самом деле,

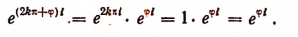
4. Исходя из формулы Эйлера, мы можем находить тригонометрические функции от комплексного числа.

Действительно, обобщая формулу 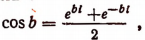примем по определению, что

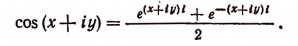
Полагая в последней формуле, например, х = 0 и у = 1, получим:

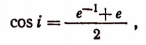
т. е. получим, что косинус мнимой единицы представляет собой действительное число.

5.Опираясь на формулу Эйлера, можно показать, что логарифм любого действительного или мнимого числа имеет в области комплексных чисел бесконечное множество различных значений. Представим комплексное число х + iy в показательной форме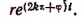

Тогда получим:

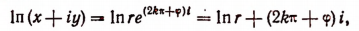
где k — любое целое число.

Под выражением In r здесь понимается лишь действительное значение логарифма положительного числа r, которое легко вычисляется по таблицам логарифмов.

Примеры:

1. Модуль числа— 1 равен 1, а главное значение аргумента равно 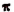. Поэтому

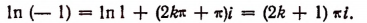
2. Модуль числа 1 есть 1, а главное значение аргумента 0. Поэтому

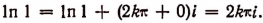
Под выражением In 1, написанным в левой части последнего равенства, подразумеваются все возможные комплексные значения логарифма единицы.

Под таким же выражением In 1, написанным в правой части, подразумевается лишь одно действительное значение логарифма единицы, т. е. нуль.

Числа е и 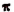являются мировыми постоянными (константы природы).

С помощью этих чисел выражаются многие законы, по которым происходят процессы в природе. Числа е и 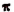, как мы уже видели, играют необычайно важную роль как в математике, так и в ее разнообразных приложениях.

Дополнение к числу е

Смотрите также:

Характер стремления In x: к бесконечности при возрастании х	Показательная функция
Шкалы порядков роста. Логарифмическая шкала	Основные свойства показательной функции

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике: