Оглавление:
Абсолютная величина действительного числа. Положение точки на прямой, на плоскости, в пространстве. Расстояние между двумя точками. Преобразование координат. Полярные координаты.
Абсолютная величина действительного числа
Определение:
Абсолютной величиной или модулем действительного числа х называется само это число, если х ≥ 0 и число -х, если х < 0:
(2.1) 
Например: |2| = 2, т. к. 2 > 0, |- 3| = -(-3) = 3, т. к. — 3 < 0,
∣x² + 4| = x² + 4, т. к. x² + 4 > О при всех х ∈ R, |0| = 0.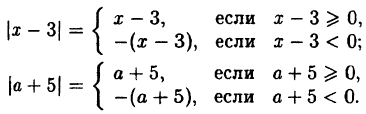
Модуль дейcтвительного числа х равен расстоянию на числовой оси от точки х до начала координат.
Расстояние между двумя точками на оси с координатами x₁ и х₂ выражается формулой:
(2.2) d = ∣x₂ — x₁∣
Докажем эту формулу для случая, когда х₂ ≥ x₁ ≥ 0 (рис. 15)
В этом случае
OM₁ = x₁ , OM₂ = x₂ и d — M₁M₂ = OM₂ — OM₁ — x₂ — x₁ — ∣ x₂ — x₁ ∣.
Если x₁>x₂ ≥ 0 (рис. 15), то d = M₁M₂ = OM₂ — OM₁ — x₁ — х₂ — (x₂ — x₁) = ∣х₂ — x₁∣ , т. к. х₂ — x₁ < 0.
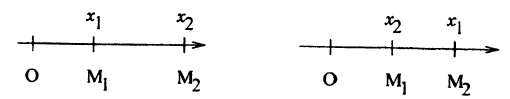
Для остальных случаев расположения M₁ и M₂ формула доказывается аналогично.
Пример:
Для данных а и R > 0 отметить на числовой оси множество M = {x|| x — а |< R}.
Решение:
В соответствии с формулой 2.2 множество M есть множество точек числовой оси, расстояние от которых до данной точки меньше R, т.е. интервал с центром в а и длиной 2R:
M = {x||x — α |< R} = {x|x ∈ (а — R; а + R)} =
= {x∣α — R < х < а + R}.
Ответ: см. рис. 16.
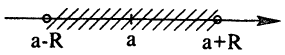
Приведем свойства модуля действительного числа, которые вытекают из определения модуля и свойств арифметических операций.
1) ∣x∣ ≥ 0,
2) ∣x∙y∣ = ∣x∣∙∣y∣,
3) 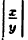 =
= 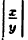
4) ∣x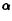 ∣ = ∣x∣
∣ = ∣x∣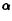 если ∃x
если ∃x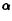 ,
,
5) |x| = |- x|,
6) |x| ≤ a ⇔ -a ≤ x ≤ а для ∀a > 0,
7) ∣x + y∣ ≤ |x| + |y|,
8) ∣x — y∣ ≤ |x| — |y|.
Заметим, что из свойств модуля и того факта, что арифметический корень квадратный неотрицателен, следует, что корень квадратный из полного квадрата некоторого выражения а равен модулю этого выражения:
(2.3) √a² = |a|.
Так, например, √5² =5; √(-3)² = 3(а не — 3);
√(x + 5)² =| x + 5|.
Аналогичное замечание справедливо при любом сокращении и показателя корня и степени подкоренного выражения на четное число:
(2.4) 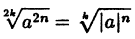 ∀k, n ∈ N
∀k, n ∈ N
Положение точки на прямой
Определение:
Координатой точки M на числовой оси называется действительное число х, которое соответствует этой точке (см. п. 1.11 лекции 2).
Положение точки на плоскости
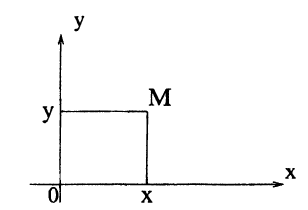
В декартовой системе координат положение точки на плоскости определяется уже двумя числами. Зададим на плоскости две взаимно перпендикулярные числовые оси Ox и Оу, имеющие общее начало О (совпадающее с точкой пересечения). Плоскость в которой, расположены оси, назовем координатной плоскостью Оху. Произвольная точка M плоскости имеет две координаты, одна из которых — ее проекция х на ось Ох, а другая ее проекция у на ось Oy (рис. 17).
Определение:
Координата х называется абсциссой точки M, а координата у — ординатой точки M. Упорядоченная пара чисел (х; у) называется прямоугольными или декартовыми координатами точки M на плоскости Оху. Каждой точке M координатной плоскости соответствует единственная упорядоченная пара чисел (х; у) и, наоборот, каждая такая пара чисел определяет единственную точку M плоскости, расположенную на пересечении перпендикуляров к осям в точках х и у соответственно. Ось Ox называется осью абсцисс, ось Oy — осью ординат, точка О — началом координат.
Заметим, что обычно горизонтальную ось называют осью абсцисс и устанавливают положительное направление направо, а вертикальную ось называют осью ординат и устанавливают положительное направление вверх, как на рис. 17. Оси Ox и Oy делят координатную плоскость на четыре четверти (на четыре квадранта): в I-й х > 0, у > 0, во II-й х < 0, у > 0, в III-й х < 0, у < 0, в IV-й х > 0, у < 0. Запись M (1; 2) будет означать, что точка M имеет абсциссу 1 и ординату 2.
Положение точки в пространстве
В декартовой системе координат положение точки в пространстве определяется тремя числами. Зададим в пространстве три взаимно перпендикулярные числовые оси Ox, Оу, Oz, имеющее общее начало О (совпадающее с точкой их пересечения). Оси назовем координатными осями: Ox — ось абцисс, Oy — ось ординат, Oz — ось аппликат. Координатное пространство обозначим Oxyz.
Произвольная точка M пространства Oxyz имеет три координаты — ее проекция х на ось Ox (пересечение плоскости, проходящей через точку M перпендикулярно оси Ох, с этой осью), ее проекция у на ось Oy и ее проекция z на ось Oz (рис. 18). Упорядоченная тройка чисел (x,y,z) называется прямоугольными или декартовыми координатами точки M в пространстве.
Очевидно, между точками в пространстве Oxyz и упорядоченными тройками чисел существует взаимно-однозначное соответствие. Координаты х, у, z называются аналогично осям — абсцисса, ордината и аппликата соответственно. Кроме координатных осей можно рассмотреть также три взаимно перпендикулярные координатные плоскости Оху, Oyz, Ozx, проходящие через оси приведенные в обозначении. Мы будем стараться располагать координатные оси как показано на рис. 18. Координатные плоскости делят пространство на 8 октантов: в I-м х > 0, у > 0, z > 0, во II-м х < 0, у > 0, z > 0, в III-м х < 0, у < 0, z > 0, в IV-M х > 0, у < 0, z > 0, в V-м х > 0, у > 0, z < 0, в VI-м х < 0, у > 0, z < 0, в VII-м х < 0, у < 0, z < 0, в VIII-м х > 0, у < 0, z < 0. Запись М(-1; -2; -3) будет означать, что точка M имеет абсциссу -1, ординату -2, аппликату -3 и расположена, следовательно, в VII октанте.
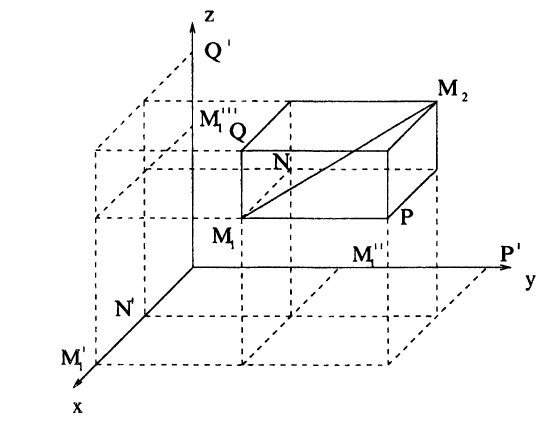
2.5. Расстояние между двумя точками. Найдем расстояние d между точками M₁(x₁,y₁, z₁) и M₂(x₂;y₂; z₂) в пространстве. Построив прямоугольный параллелепипед, диагональю которого является отрезок M₁M₂ и с гранями, параллельными координатным плоскостям (рис. 19), на основании известной теоремы курса стереометрии средней школы получим:
M₁M₂² = M₁N² + M₁P² + M₁Q².
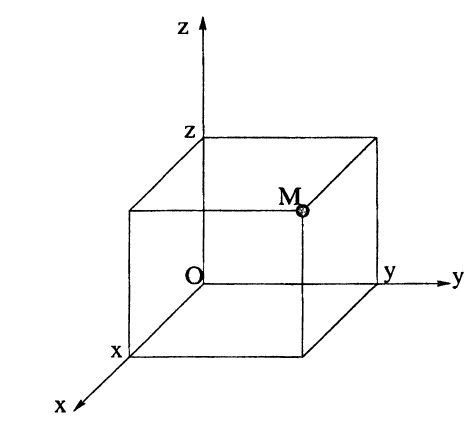
Спроектировав концы ребер M₁N, M₁P, M₁Q на оси Ox, Оу, Oz, получим на этих осях отрезки M’₁N’, M»₁P’, M»’₁ Q1 и в соответствии с формулой ( 2.2): M₁N = M’₁N’ = ∣x₂ — x₁∣; M₁P = M₁»P’ = ∣y₂ — y₁∣; M₁Q = M₁»Q’ = ∣z₂ — z₁∣.
Подставив эти выражения в предыдущую формулу, получим:
M₁M₂² = ∣x₂ — x₁∣² + ∣y₂ — y₁∣² + ∣z₂ — z₁∣²,
или:
(2.5) 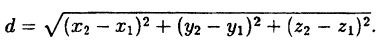
Данная формула остается, безусловно, справедливой, если отрезок M₁M₂ параллелен каким-либо координатным плоскостям (рассмотрите эти случаи самостоятельно). Если точки M₁ (x₁; y₁) и М₂ (х₂; у₂) лежат в плоскости Оху, то формула для расстояния между этими точками принимает вид:
(2.6) 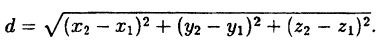
Пример:
Найти расстояние d₁ между точками M₁ (-1; -2; -3;) и M₂ (0; -2; 5), расстояние d₂ между точками М₃ (2;3) и М₄ (—1;0) и расстояние d₃ между началом координат 0 и точкой M₅ (-2; 1; 3).
Решение:
По формуле ( 2.5):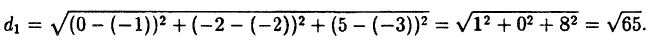
По формуле ( 2.6):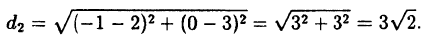
По формуле ( 2.5):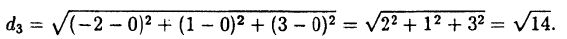
Параллельный перенос осей координат
В некоторых случаях приходится одновременно рассматривать две системы координат на плоскости и решать следующую задачу: зная координаты точки в одной системе координат, найти ее координаты в другой системе. Эти формулы называются формулами преобразования координат.
Мы будем предполагать, что обе системы — декартовы (прямоугольные), причем одноименные оси этих систем параллельны и одинаково направлены, и на каждой из осей выбрана одна и та же масштабная единица. На рис. 20 изображены две такие системы Oxy и O₁XY. Система O₁XY может быть получена параллельным переносом осей Ox и Оу.
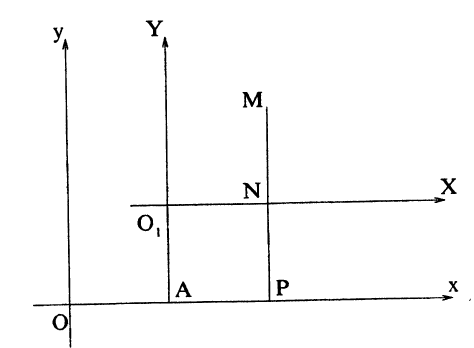
Условимся называть координаты точек в системе Oxy старыми, а в системе O₁XY — новыми. Пусть x₀, y₀ — координаты нового начала O₁ в старой системе. Предположим, что произвольно выбранная точка M на плоскости имеет старые координаты х и у и новые координаты X и Y. Выведем формулы, выражающие старые координаты точки M через новые. Проектируя новое начало O₁ и точку M на ось Ох, а также точку M на ось O₁X, получим соответственно точки A, P и N. Очевидно, O₁N = АР. Но O₁N = |X|, AP = |х — x₀∣, тaκ что
|X| =∣x-x₀∣ ,
т.е. новая абсцисса X и разность x-x₀ равны по модулю. Нетрудно заметить, что и знаки этих величин одинаковы. В самом деле, если N лежит правее O₁ , то P расположена правее А, и обе величины X и (x-x₀) положительны. Если же N находится левее O₁, то P — левее А и, следовательно, X и (x-x₀) отрицательны. В обоих случаях X = x-x₀,
откуда х = X + x₀. Аналогично получается формула для старой ординаты у. Таким образом, мы получили следующие формулы преобразования координат (параллельного переноса осей):
(2.7) х = X + x₀ > У = Y + y₀
Пример:
Дана точка M(2; —1) в системе Оху. Найти ее новые координаты X и Y при параллельном переносе осей, если новое начало в старой системе имеет координаты -1 и 3.
Решение:
По формулам ( 2.7) получим 2 = X — 1, -1 = Y + 3, откуда X = 3, Y = -4
Полярные координаты
Наряду с декартовыми координатами на плоскости употребляются полярные координаты, в которых положение точки M на плоскости задается (рис. 21) полярным углом  и полярным радиусом r, называемыми полярными координатами точки M : M(
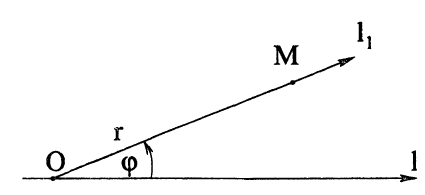
и полярным радиусом r, называемыми полярными координатами точки M : M( ∙,r). Пусть на плоскости задана числовая ось l. Назовем ее полярной осью, а ее начало — точку О — полюсом. Проведем через точку M и полюс ось l₁, начало которой совпадает с О (см. рис. 21), а положительное направление от О к М. Полярный угол
∙,r). Пусть на плоскости задана числовая ось l. Назовем ее полярной осью, а ее начало — точку О — полюсом. Проведем через точку M и полюс ось l₁, начало которой совпадает с О (см. рис. 21), а положительное направление от О к М. Полярный угол  — это угол между полярной осью 1 и осью l₁, отсчитываемый со знаком «+» против часовой стрелки и со знаком «-» по часовой стрелке. Полярный радиус r — это расстояние от О до точки M по оси l₁ (r ≥ 0). Если значение полярного угла
— это угол между полярной осью 1 и осью l₁, отсчитываемый со знаком «+» против часовой стрелки и со знаком «-» по часовой стрелке. Полярный радиус r — это расстояние от О до точки M по оси l₁ (r ≥ 0). Если значение полярного угла  ограничить промежутком 0 ≤
ограничить промежутком 0 ≤  < 2π, то между точками плоскости и упорядоченными парами полярных координат (
< 2π, то между точками плоскости и упорядоченными парами полярных координат ( ; r) будет существовать взаимно-одназначное соответствие.
; r) будет существовать взаимно-одназначное соответствие.
Пример:
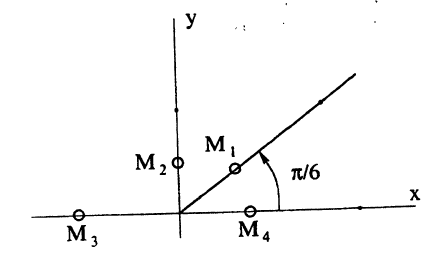
Построить в полярной системе координат точки 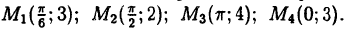
Решение:
Точки M₁, M₂, M₃, M₄, отмечены на рис. 22
Выведем формулы, связывающие декартовы и полярные координаты точки на плоскости, для чего расположим полярную ось l, совпадающую с осью Ox, а полюс О — с началом координат О (рис. 23)
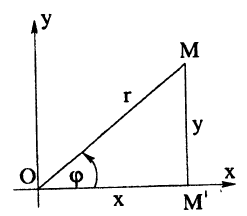
Из Δ OMM’ находим: cos  =
= 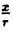 , sin
, sin  =
=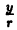 , r² = r² + у², откуда:
, r² = r² + у², откуда:
(2.8) 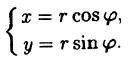
(2.9)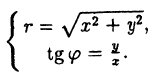
Легко понять,что формулы ( 2.8), ( 2.9) будут справедливы при любом расположении точки M на плоскости. Формулы ( 2.8) дают зависимость декартовых координат (x∙,y) от полярных (r, ), а формулы ( 2.9) — наоборот. В последней формуле ( 2.9) из двух значений угла
), а формулы ( 2.9) — наоборот. В последней формуле ( 2.9) из двух значений угла  , соответствующих найденной величине tg
, соответствующих найденной величине tg , выбирается то (0 ≤
, выбирается то (0 ≤  < 2π), при котором удовлетворяются условия ( 2.8).
< 2π), при котором удовлетворяются условия ( 2.8).
Пример:
Найти полярные координаты точки M с декартовыми координатами х = 2, у =-2.
Решение:
По формулам ( 2.9) находим : r = 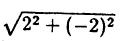 =
= 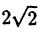 , tg
, tg 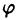 = — 1 Найдем угол
= — 1 Найдем угол  : tg
: tg = — 1 ⇒
= — 1 ⇒  = arctg(-1) + nπ, n ∈ Z ⇔
= arctg(-1) + nπ, n ∈ Z ⇔  =
= 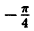 + nπ, n ∈ Z Условию 0 ≤
+ nπ, n ∈ Z Условию 0 ≤ 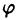 < 2π, удовлетворяют два значения:
< 2π, удовлетворяют два значения:  ₁ =
₁ = 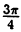 , и
, и  ₂ =
₂ = 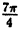 , однако равенства ( 2.8):
, однако равенства ( 2.8):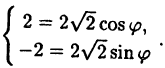
удовлетворяются только при  =
= 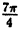 . Ответ: M(
. Ответ: M(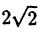 ;
; 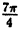 ).
).
Поворот осей координат
Пусть на плоскости заданы две системы координат, имеющие общее начало О: система Oxy (старая) и система OXY (новая), которая получена поворотом старой системы на угол а. Это значит,что угол (Ox;OX) = а (рис. 24) и, следовательно, угол (Oy, OY) = а. Найдем формулы, выражающие старые координаты х и у произвольной точки M плоскости через ее новые координаты X и Y.
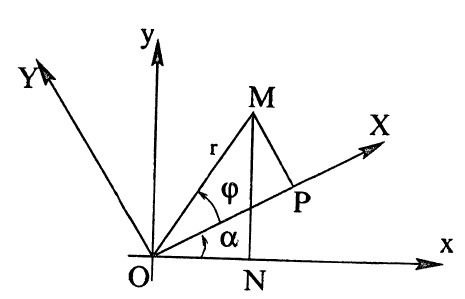
Введем полярные координаты: старые — с полярной осью, совпадающей с осью Ох, и новые — с полярной осью ОХ. Пусть точка M в новой
полярной системе имеет полярный угол 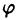 и полярный радиус r. В старой полярной системе полярный угол точки M равен α +
и полярный радиус r. В старой полярной системе полярный угол точки M равен α +  , а полярный радиус такой же, как и в новой системе. Поэтому по формулам ( 2.8) имеем:
, а полярный радиус такой же, как и в новой системе. Поэтому по формулам ( 2.8) имеем:
х = r cos (α +  ), у = r sin (α +
), у = r sin (α +  ).
).
Используя тригонометрические тождества для косинуса и синуса суммы двух углов, получим:
х = r (cos α cos  — sin α sin
— sin α sin 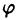 ) = (r cos
) = (r cos  ) cos α — (r sin
) cos α — (r sin  ) sin α;
) sin α;
у = r (sin α cos 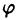 + cos α sin
+ cos α sin  ) = (r cos
) = (r cos  ) sin α + (r sin
) sin α + (r sin  )cos α.
)cos α.
Ho r cos  = X и r sin
= X и r sin  = Y, поэтому
= Y, поэтому
(2.10) x = X cos α -Y sin α, у = X sin α + Y cos α.
Формулы ( 2.10) называются формулами поворота осей. Выразив отсюда X и Y, получим
(2.11) X = x cos α + y sin α, Y =-x sin α + у cos α.
Пример:
Выразить старые координаты точки х и у через ее новые координаты X и Y при повороте осей на угол α = π∕4.
Решение:
Так как cos(π∕4) = √2∕2, то по формулам ( 2.10) получим: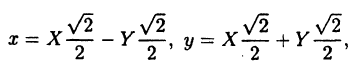
или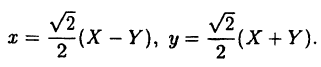
Системы координат — примеры с решением
В этом практическом занятии на основании материала лекций 1 и 2 решите примеры с модулями, а также — на преобразование координат.
Пример:
Запишите с помощью знака модуля неравенство -3 < х < 3.
Решение:
Неравенство -3 < х < 3 на основании свойства 6 модуля действительного числа (лекция 2) равносильно неравенству |х| < 3.
Ответ: -3 < х < 3 ⇔|x| < 3.
Пример:
Решите неравенство |х — 1| < 5.
Решение:
Неравенство можно решить с помощью свойства 6 модуля действительного числа (2), однако здесь целесообразно использовать определение модуля: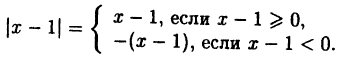
Исходное неравенство равносильно совокупности двух систем: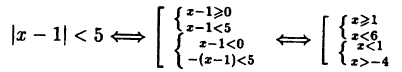
Решение последней совокупности представлено на рис. 25. Следует
помнить, что решение системы неравенств получается как пересечение множеств решений каждого, а решение совокупности систем (неравенств) получается как объединение множеств решений каждой.
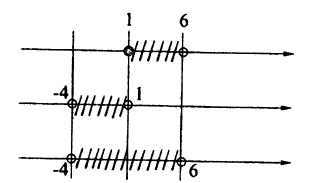
Для решения этого примера можно также воспользоваться решением примера 1.1 лекции 2.
Ответ: х ∈ (—4;6).
Система координат на плоскости



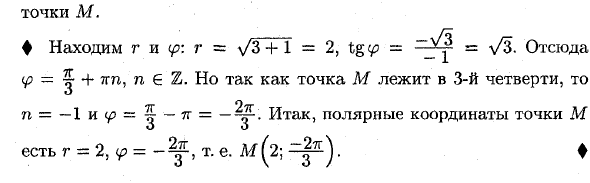
Смотрите также:
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

