Оглавление:

| Здравствуйте! Я Людмила Анатольевна Фирмаль, занимаюсь помощью студентам более 17 лет. У меня своя команда грамотных, сильных преподавателей. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И неважно – она по объёму на две формулы или огромная, сложно структурированная, на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте. |
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Как заказать выполнение заданий по теории вероятностей
Вы можете написать сообщение в WhatsApp. После этого я оценю ваш заказ и укажу стоимость и срок выполнения вашей работы. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за вашу работу, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл готовой работы в личные сообщения.
Сколько может стоить заказ теории вероятности
Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости, загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Какой срок выполнения заказа
Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Как оплатить заказ
Сначала пришлите задание, я оценю, после вышлю вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Гарантии и исправление ошибок
В течение 1 года с момента получения Вами готового решения заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Чуть ниже я предоставила примеры оформления заказов по некоторым темам теории вероятностей, так я буду оформлять ваши работы если закажите у меня, это не все темы, это лишь маленькая часть их, чтобы вы понимали насколько подробно я оформляю.
Возможно эта страница вам будет полезна:
| Предмет теория вероятностей и математическая статистика |
Пример оформления заказа №1.
В розыгрыше кубка страны по футболу берут участие 17 команд. Сколько существует способов распределить золотую, серебряную и бронзовую медали?
Решение:
Поскольку медали не равноценны, то количество способов распределить золотую, серебряную и бронзовую медали среди команд будет равно числу размещений из 17-ти элементов по 3, т.е.
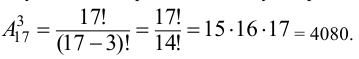
Пример оформления заказа №2.
Произведено три выстрела по мишени. Рассматриваются такие элементарные события: 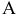 — попадание в мишень при
— попадание в мишень при 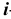 -том выстреле;
-том выстреле; 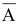 — промах по мишени при
— промах по мишени при 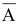 -том выстреле. Выразить через
-том выстреле. Выразить через 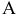 и
и 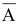 следующие события:
следующие события:
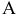 — все три попадания;
— все три попадания; 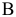 — ровно два попадания;
— ровно два попадания; 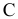 — все три промаха;
— все три промаха; 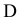 — хотя бы одно попадание;
— хотя бы одно попадание; 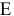 — больше одного попадания;
— больше одного попадания; 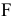 — не больше одного попадания.
— не больше одного попадания.
Решение:
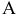 — все три попадания, т.е. совместное появления трех событий
— все три попадания, т.е. совместное появления трех событий
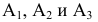
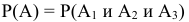
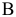 — ровно два попадания, т.е. два попадания и один промах
— ровно два попадания, т.е. два попадания и один промах
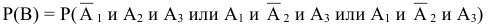
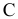 — все три промаха, т.е. совместное появления трех событий
— все три промаха, т.е. совместное появления трех событий
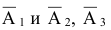
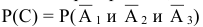
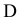 — хотя бы одно попадание, т.е. или одно попадание, или два попадания или три попадания
— хотя бы одно попадание, т.е. или одно попадание, или два попадания или три попадания
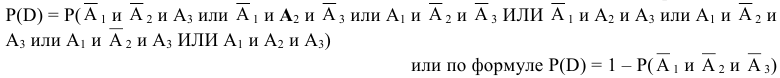
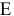 — больше одного попадания, т.е. или два попадания или три попадания
— больше одного попадания, т.е. или два попадания или три попадания
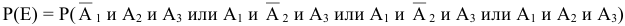
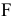 — не больше одного попадания, т.е. одно попадание и два промаха
— не больше одного попадания, т.е. одно попадание и два промаха
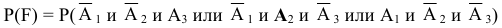
Пример оформления заказа №3.
Игральный кубик бросают два раза. Описать пространство элементарных событий. Описать события: 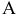 — сумма появившихся очков равна 8;
— сумма появившихся очков равна 8; 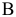 — по крайней мере один раз появится 6.
— по крайней мере один раз появится 6.
Решение:
Будем считать пространством элементарных событий множество пар чисел 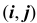 , где
, где 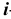 (соответственно
(соответственно 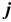 ) есть число очков, выпавших при первом (втором) подбрасывании, тогда множество элементарных событий будет таким:
) есть число очков, выпавших при первом (втором) подбрасывании, тогда множество элементарных событий будет таким:

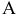 — сумма появившихся очков равна 8. Этому событию благоприятствуют такие элементарные события
— сумма появившихся очков равна 8. Этому событию благоприятствуют такие элементарные события
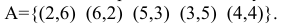
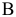 — по крайней мере один раз появится 6. Этому событию благоприятствуют такие элементарные события
— по крайней мере один раз появится 6. Этому событию благоприятствуют такие элементарные события
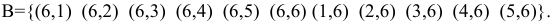
Пример оформления заказа №4.
В вазе с цветами 15 гвоздик: 5 белых и 10 красных. Из вазы наугад вынимают 2 цветка. Какова вероятность того, что эти цветки: а) оба белые; б) оба красные; в) разного цвета; г) одного цвета.
Решение:
а) Пусть событие 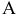 состоит в том, что оба вынутых из вазы цветка белые.
состоит в том, что оба вынутых из вазы цветка белые.
Количество возможных способов взять 2 цветка из 15-ти равно 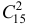 , т.е.
, т.е.
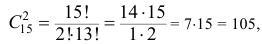
а количество возможных способов взять 2 белых цветка из 5-ти белых равно
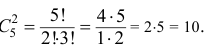
Тогда по классическому определению вероятность события 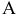 равна
равна
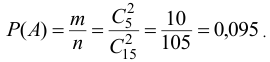
б) Пусть событие 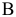 состоит в том, что оба вынутых из вазы цветка красные. Количество возможных способов взять 2 цветка из 15-ти равно
состоит в том, что оба вынутых из вазы цветка красные. Количество возможных способов взять 2 цветка из 15-ти равно 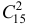 , т.е.
, т.е.
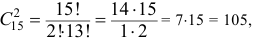
а количество возможных способов взять 2 красных цветка из 10-ти красных равно
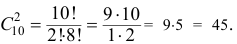
Тогда по классическому определению вероятность события 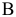 равна
равна
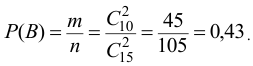
в) Пусть событие 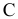 состоит в том, что оба вынутых из вазы цветка разного цвета, т.е. один белый и один красный.
состоит в том, что оба вынутых из вазы цветка разного цвета, т.е. один белый и один красный.
Количество возможных способов взять 2 цветка из 15-ти равно 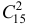 , т.е.
, т.е.
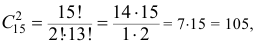
а количество возможных способов взять 1 красный цветок из 10-ти красных и 1 белый цветок из 5-ти белых равно
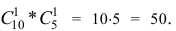
Тогда по классическому определению вероятность события 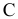 равна
равна
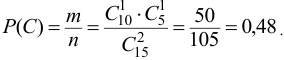
г) Пусть событие 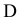 состоит в том, что оба вынутых из вазы цветка одного цвета, т.е. или оба белые (событие
состоит в том, что оба вынутых из вазы цветка одного цвета, т.е. или оба белые (событие 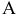 ) или оба красные (событие
) или оба красные (событие 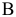 ). По теореме сложения независимых событий вероятность события
). По теореме сложения независимых событий вероятность события 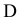 будет равна
будет равна
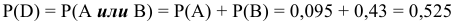
Пример оформления заказа №5.
Из шести карточек с буквами 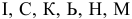 наугад одну за другой вынимают и раскладывают в ряд в порядке появления. Какова вероятность того, что появится слово а) «НIС»; б) «СIМ»?
наугад одну за другой вынимают и раскладывают в ряд в порядке появления. Какова вероятность того, что появится слово а) «НIС»; б) «СIМ»?
Решение: (для пунктов а) и б) одинаково)
Каждый вариант получившегося «слова» является размещением из 6-ти элементов по 3.
Число таких вариантов равно
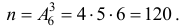
Из этих вариантов правильным будет только один, т.е. 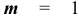 , тогда по классическому определению вероятности
, тогда по классическому определению вероятности
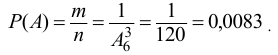
Пример оформления заказа №6.
Вероятность того, что в течении одной смены возникнет поломка станка равна 0,05. Какова вероятность того, что не возникнет ни одной поломки за три смены?
Решение:
Пусть событие 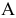 состоит в том, что в течении одной смены возникнет поломка станка. По условию задачи вероятность этого события равна
состоит в том, что в течении одной смены возникнет поломка станка. По условию задачи вероятность этого события равна 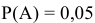 . Противоположное событие
. Противоположное событие 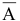 состоит в том, что в течении одной смены поломка станка НЕ возникнет. Вероятность противоположного события
состоит в том, что в течении одной смены поломка станка НЕ возникнет. Вероятность противоположного события
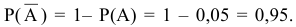
Искомая вероятность равна
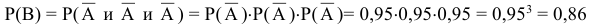
Пример оформления заказа №7.
Студент пришел на зачет зная только 30 вопросов из 50. Какова вероятность сдачи зачета, если после отказа отвечать на вопрос преподаватель задает еще один?
Решение:
Вероятность того, что преподаватель задал студенту вопрос, на который он не знал ответа (событие 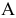 ) равна
) равна 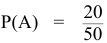 . Найдем вероятность того, что на второй вопрос преподавателя студент знает ответ (событие
. Найдем вероятность того, что на второй вопрос преподавателя студент знает ответ (событие 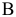 ) при условии, что ответа на первый вопрос студент не знал. Это условная вероятность, так как событие
) при условии, что ответа на первый вопрос студент не знал. Это условная вероятность, так как событие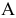 уже произошло. Отсюда
уже произошло. Отсюда 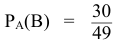 . Искомую вероятность определим по теореме умножения вероятностей зависимых событий.
. Искомую вероятность определим по теореме умножения вероятностей зависимых событий.
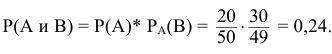
Пример оформления заказа №8.
С помощью наблюдений установлено, что в некоторой местности в сентябре в среднем бывает 12 дождливых дней. Какова вероятность того, что из наугад взятых в этом месяце 8-ми дней 3 будут дождливыми?
Решение:
Поскольку количество испытаний невелико 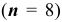 , то для нахождения вероятности того, что событие
, то для нахождения вероятности того, что событие 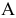 появится точно
появится точно 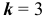 раза воспользуемся формулой Бернулли:
раза воспользуемся формулой Бернулли:
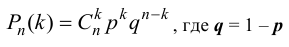
По условию задачи вероятность дождя равна 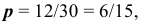 (в сентябре 30 дней). Значит вероятность ясного дня равна
(в сентябре 30 дней). Значит вероятность ясного дня равна 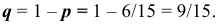
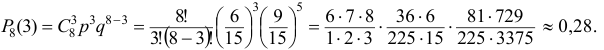
Пример оформления заказа №9.
С помощью наблюдений установлено, что в некоторой местности в сентябре в среднем бывает 25 дней без дождя. Какова вероятность того, что 1-го и 2-го сентября дождя не будет?
Решение:
Вероятность того, что 1-го сентября дождя не будет (событие 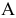 ) равна
) равна 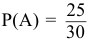 . Найдем вероятность того, что и 2-го сентября дождя не будет (событие
. Найдем вероятность того, что и 2-го сентября дождя не будет (событие 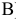 ) при условии, что 1-го сентября дождя не было. Это условная вероятность, так как событие
) при условии, что 1-го сентября дождя не было. Это условная вероятность, так как событие 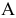 уже произошло.
уже произошло.
Отсюда 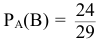 . Искомую вероятность определим по теореме умножения вероятностей зависимых событий.
. Искомую вероятность определим по теореме умножения вероятностей зависимых событий.
Пример оформления заказа №10.
В условиях задачи 8 найти вероятность наивероятнейшего числа дней без ДОЖДЯ. (Задача 8. С помощью наблюдении установлено, что в некоторой местности в сентябре в среднем бывает 12 дождливых дней. Какова вероятность того, что из наугад взятых в этом месяце 8-ми дней 3 будут дождливыми?)
Решение:
Число 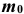 называется наивероятнейшим в
называется наивероятнейшим в 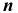 независимых испытаниях, если вероятность наступления события
независимых испытаниях, если вероятность наступления события 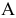 при этом числе наибольшая.
при этом числе наибольшая.
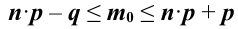
По условию задачи 8 вероятность дня без дождя равна 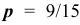 , значит вероятность дождливого дня равна
, значит вероятность дождливого дня равна 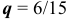 . Составим неравенство
. Составим неравенство
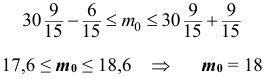
Наивероятнейшее число дней без дождя равно 18. Поскольку количество испытаний велико 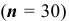 и нет возможности применить формулу Бернулли, то для нахождения вероятности наивероятнейшего числа дней без дождя воспользуемся локальной теоремой Лапласа:
и нет возможности применить формулу Бернулли, то для нахождения вероятности наивероятнейшего числа дней без дождя воспользуемся локальной теоремой Лапласа:
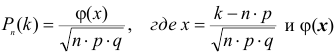
— диф. функция Лапласа -Гаусса
Определим аргумент функции Лапласа-Гаусса 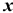 : 4
: 4
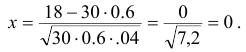
По таблице значений функции Гаусса определяем, что
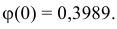
Теперь
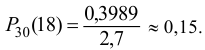
Пример оформления заказа №11.
Вероятность получения удачного результата при проведении сложного химического опыта равна 3/4. Найти вероятность шести удачных результатов в 10-ти опытах.
Решение:
Поскольку количество испытаний невелико 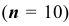 , то для нахождения вероятности того, что событие
, то для нахождения вероятности того, что событие 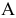 появится точно
появится точно 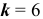 раз воспользуемся формулой Бернулли:
раз воспользуемся формулой Бернулли:
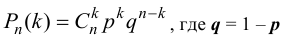
По условию задачи 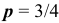 , значит
, значит 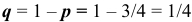 .
.
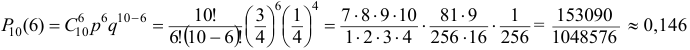
Пример оформления заказа №12.
Вероятность рождения мальчика равна 0,515, девочки — 0,485. В некоторой семье шестеро детей. Найти вероятность того, что среди низ не больше двух девочек.
Решение:
Пусть событие 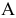 состоит в том, что в семье, где шестеро детей, не больше двух девочек, т.е. в указанной семье или одна девочка или две девочки или все мальчики. Поскольку количество испытаний невелико
состоит в том, что в семье, где шестеро детей, не больше двух девочек, т.е. в указанной семье или одна девочка или две девочки или все мальчики. Поскольку количество испытаний невелико 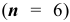 , то для нахождения вероятности события
, то для нахождения вероятности события 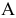 воспользуемся формулой Бернулли:
воспользуемся формулой Бернулли:
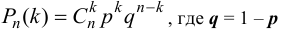
По условию задачи вероятность рождения девочки равна 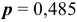 и вероятность рождения мальчика равна
и вероятность рождения мальчика равна 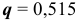 , тогда искомая вероятность будет равна
, тогда искомая вероятность будет равна
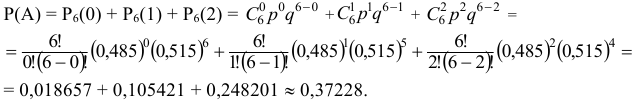
Пример оформления заказа №13.
Что вероятнее: выиграть у равносильного противника (включая ничью) три партии из пяти или пять из восьми?
Решение:
Вероятность выиграть у равносильного противника равна 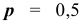 , соответственно вероятность проиграть у равносильного противника равна
, соответственно вероятность проиграть у равносильного противника равна 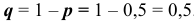 . Найдем и сравним такие вероятность
. Найдем и сравним такие вероятность 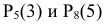 .
.
Поскольку количество испытаний невелико 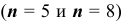 , то для нахождения вероятности того, что событие
, то для нахождения вероятности того, что событие 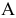 появится точно
появится точно 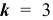 раза
раза 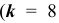 раз) воспользуемся формулой Бернулли:
раз) воспользуемся формулой Бернулли:
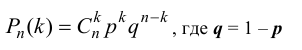
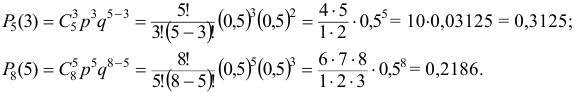
Сравнивая полученные значения вероятностей
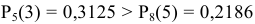
получаем, что вероятнее выиграть у равносильного противника три партии из пяти чем пять из восьми.
Пример оформления заказа №14.
Из партии, в которой 25 изделий, среди которых 6 бракованных, случайным образом выбрали 3 изделия для проверки качества. Найти вероятность того, что: а) все изделия годные, б) среди выбранных изделий одно бракованное; в) все изделия бракованные.
Решение:
а) Пусть событие 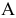 состоит в том, что все выбранные изделия годные. Количество возможных способов взять 3 изделия из 25-ти равно
состоит в том, что все выбранные изделия годные. Количество возможных способов взять 3 изделия из 25-ти равно 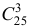 , т.е.
, т.е.
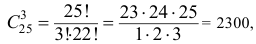
а количество возможных способов взять 3 годных изделия из (25 — 6) = 19-ти годных равно
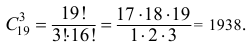
Тогда по классическому определению вероятность события 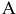 равна
равна
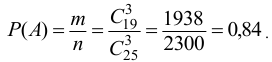
б) Пусть событие 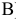 состоит в том, что среди выбранных изделий одно бракованное, т.е. одно бракованное и два годных. Количество возможных способов взять 3 изделия из 25-ти равно
состоит в том, что среди выбранных изделий одно бракованное, т.е. одно бракованное и два годных. Количество возможных способов взять 3 изделия из 25-ти равно 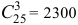 , а количество возможных способов взять одно бракованное изделие из 6-ти бракованных И два годных изделия из (25 — 6) = 19-ти годных равно
, а количество возможных способов взять одно бракованное изделие из 6-ти бракованных И два годных изделия из (25 — 6) = 19-ти годных равно
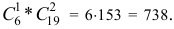
Тогда по классическому определению вероятность события 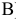 равна
равна
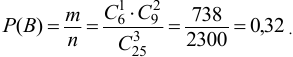
в) Пусть событие 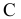 состоит в том, что все выбранные изделия бракованные. Количество возможных способов взять 3 изделия из 25-ти равно
состоит в том, что все выбранные изделия бракованные. Количество возможных способов взять 3 изделия из 25-ти равно 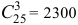 , а количество возможных способов взять 3 бракованные изделия из 6-ти бракованных равно
, а количество возможных способов взять 3 бракованные изделия из 6-ти бракованных равно
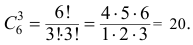
Тогда по классическому определению вероятность события 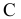 равна
равна
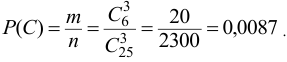
Пример оформления заказа №15.
В условиях задачи 13 найти наивероятнейшее число удачных опытов и вероятность его появления. (Задача 11. Вероятность получения удачного результата при проведении сложного химического опыта равна 3/4. Найти вероятность шести удачных результатов в 10-ти опытах).
Решение:
Число 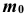 называется наивероятнейшим в
называется наивероятнейшим в 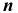 независимых испытаниях, если вероятность наступления события
независимых испытаниях, если вероятность наступления события 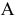 при этом числе наибольшая.
при этом числе наибольшая.
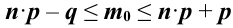
По условию задачи 11 вероятность проведения удачного опыта равна 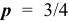 , значит вероятность неудачного опыта равна
, значит вероятность неудачного опыта равна 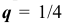 . Количество опытов равно
. Количество опытов равно 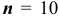 . Составим неравенств
. Составим неравенств
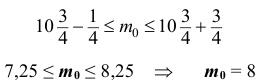
Наивероятнейшее число удачных опытов равно 8. Поскольку количество испытаний невелико (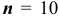 ), то для нахождения вероятности того, что событие
), то для нахождения вероятности того, что событие 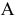 появится точно
появится точно 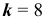 раз воспользуемся формулой Бернулли:
раз воспользуемся формулой Бернулли:
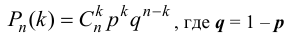
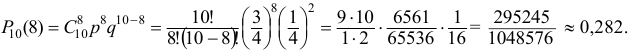
Пример оформления заказа №16.
В белом ящике 12 красных и 6 синих шаров. В черном — 15 красных и 10 синих шаров. Бросают игральный кубик. Если выпадет количество очков, кратное 3, то наугад берут шар из белого ящика. Если выпадет любое другое количество очков, то наугад берут шар из черного ящика. Какова вероятность появления красного шара?
Решение:
Возможны две гипотезы:
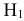 — при бросании кубика выпадет количество очков, кратное 3, т.е. или 3 или 6;
— при бросании кубика выпадет количество очков, кратное 3, т.е. или 3 или 6;
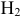 — при бросании кубика выпадет другое количество очков, т.е. или 1 или 2 или 4 или 5.
— при бросании кубика выпадет другое количество очков, т.е. или 1 или 2 или 4 или 5.
По классическому определению вероятности гипотез равны:
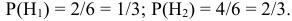
Поскольку гипотезы составляют полную группу событий, то должно выполняться равенство
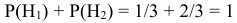
Пусть событие 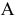 состоит в появлении красного шара. Условные вероятности этого события зависят от того, какая именно гипотеза реализовалась, и составляют соответственно:
состоит в появлении красного шара. Условные вероятности этого события зависят от того, какая именно гипотеза реализовалась, и составляют соответственно:

Тогда по формуле полной вероятности
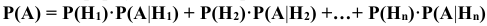
вероятность события 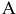 будет равна:
будет равна:
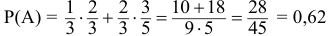
Пример оформления заказа №17.
Вероятность появления события 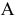 по крайней мере один раз в 5-ти независимых испытаниях равна 0,9. Какова вероятность появления события
по крайней мере один раз в 5-ти независимых испытаниях равна 0,9. Какова вероятность появления события 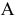 в одном испытании, если при каждом испытании она одинаковая?
в одном испытании, если при каждом испытании она одинаковая?
Решение:
Воспользуемся формулой для вероятности появления хотя бы одного события
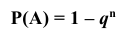
По условию задачи
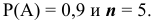
Составим уравнение
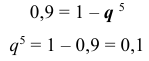
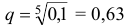 — вероятность Не появления события
— вероятность Не появления события 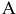 в одном испытании, тогда
в одном испытании, тогда 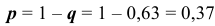 — вероятность появления события
— вероятность появления события 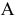 в одном испытании.
в одном испытании.
Пример оформления заказа №18.
Из каждых 40-ка изделий, изготовленных станком-автоматом 4 бракованных. Наугад взяли 400 изделий. Найти вероятность того, что среди них 350 без дефекта.
Решение:
Поскольку количество испытаний велико 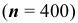 то для нахождения вероятности того, что событие
то для нахождения вероятности того, что событие 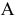 появится ровно
появится ровно 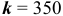 раз воспользуемся локальной теоремой Лапласа:
раз воспользуемся локальной теоремой Лапласа:
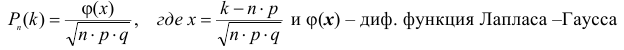
По условию задачи вероятность бракованного изделия равна
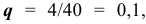
Значит вероятность изделия без дефекта равна
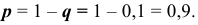
Определим аргумент функции Лапласа-Гаусса 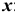 :
:
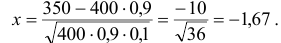
Учитывая что функция 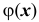 является четной, т.е.
является четной, т.е. 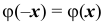 по таблице значений функции Гаусса определяем, что
по таблице значений функции Гаусса определяем, что
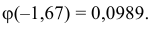
Теперь
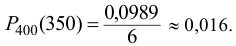
Пример оформления заказа №19.
Вероятность присутствия студента на лекции равна 0,8. Найти вероятность того, что из 100 студентов на лекции будут присутствовать не меньше 75 и не больше 90.
Решение:
Поскольку количество испытаний велико 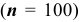 , то для нахождения вероятности того, что событие
, то для нахождения вероятности того, что событие 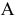 появится от 75 до 90 раз воспользуемся интегральной теоремой Лапласа:
появится от 75 до 90 раз воспользуемся интегральной теоремой Лапласа:
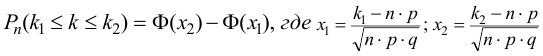
и 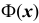 — интегральная функция Лапласа Определим аргументы интегральной функции Лапласа
— интегральная функция Лапласа Определим аргументы интегральной функции Лапласа 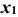 и
и 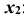 :
:
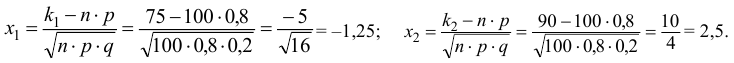
Учитывая что функция 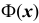 является Нечетной, т.е.
является Нечетной, т.е.
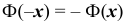
по таблице значений интегральной функции Лапласа находим:
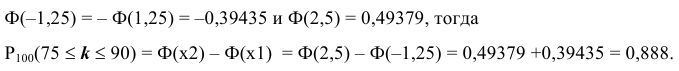
Пример оформления заказа №20.
Сколько раз необходимо кинуть игральный кубик, чтобы навероятнейшее число появления тройки равнялось 55?
Решение:
Число 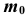 называется наивероятнейшим в
называется наивероятнейшим в 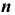 независимых испытаниях, если вероятность наступления события
независимых испытаниях, если вероятность наступления события 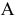 при этом числе наибольшая.
при этом числе наибольшая.
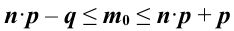
По условию задачи 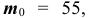 , вероятность появления тройки равна
, вероятность появления тройки равна 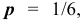 значит вероятность НЕ появления тройки равна
значит вероятность НЕ появления тройки равна 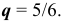 . Составим неравенство
. Составим неравенство
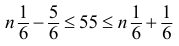
получили линейную систему неравенств
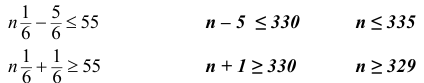
Таким образом получили, что игральный кубик необходимо кинуть от 329 до 335 раз.
Пример оформления заказа №21.
Ткач обслуживает 1000 веретен. Вероятность обрыва нитки на одном из веретен в течении одной минуты равна 0,005. Найти вероятность того, что в течении одно минуты обрыв произойдет на 7 веретенах.
Решение:
Поскольку количество испытаний велико 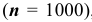 , а вероятность отдельного испытания очень мала
, а вероятность отдельного испытания очень мала 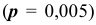 то для вычисления искомой вероятности воспользуемся формулой Пуассона:
то для вычисления искомой вероятности воспользуемся формулой Пуассона:
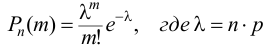
Параметр распределения
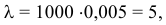
тогда искомая вероятность равна
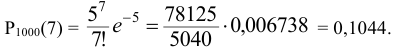
Пример оформления заказа №22.
Задан закон распределения дискретной случайной величины 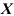 :
:

Найти функцию распределения и построить ее график.
Решение:
Функцией распределения называют функцию 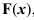 , определяющую вероятность того, что случайная величина
, определяющую вероятность того, что случайная величина 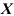 в результате испытания примет значение, меньшее некоторого фиксированного значения
в результате испытания примет значение, меньшее некоторого фиксированного значения 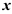
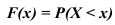
В нашем случае

Таким образом функция распределения 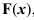 имеет вид:
имеет вид:
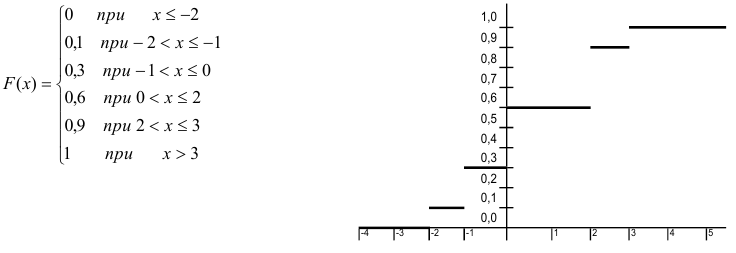
Пример оформления заказа №23.
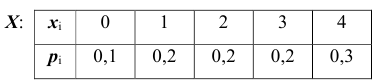
Задан закон распределения дискретной случайной величины 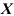 :
:
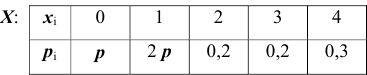
Найти функцию распределения и построить ее график.
Решение:
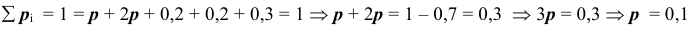
Следовательно закон распределения дискретной случайной величины  примет вид:
примет вид:
Функцией распределении называют функцию 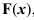 , определяющую вероятность того, что случайная величина
, определяющую вероятность того, что случайная величина 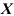 в результате испытания примет значение, меньшее некоторого фиксированного значения
в результате испытания примет значение, меньшее некоторого фиксированного значения 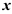
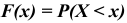
В нашем случае

Таким образом функция распределения 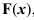 имеет вид:
имеет вид:
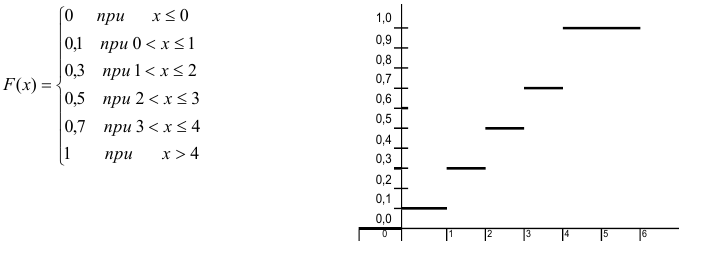
Пример оформления заказа №24.
Монета брошена 2 раза. Записать закон распределения CЛ вел 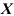 — числа появления герба.
— числа появления герба.
Найти функцию распределения и построить ее график.
Решение:
Обозначим вероятность появления «герба» при подбрасывании одной монеты через 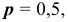 тогда
тогда 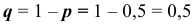 — вероятность появления надписи.
— вероятность появления надписи.
Случайная величина 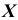 — число появления герба. Она может принимать следующие возможные значения: 0, 1,2. Найдем вероятности, с которыми случайная величина
— число появления герба. Она может принимать следующие возможные значения: 0, 1,2. Найдем вероятности, с которыми случайная величина 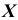 может принимать эти возможные значения:
может принимать эти возможные значения:
при 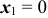 — оба раза выпала надпись, тогда
— оба раза выпала надпись, тогда
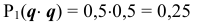
при 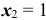 — один раз выпал «герб» и один раз — надпись, тогда
— один раз выпал «герб» и один раз — надпись, тогда
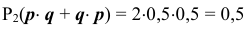
при 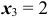 — оба раза выпал «герб», тогда
— оба раза выпал «герб», тогда
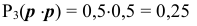
ТОГДА закон распределения дискретной случайной величины 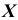 примет вид:
примет вид:
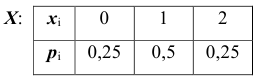
Проверка
Функцией распределения называют функцию 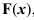 , определяющую вероятность того, что случайная величина
, определяющую вероятность того, что случайная величина 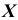 в результате испытания примет значение, меньшее некоторого фиксированного значения
в результате испытания примет значение, меньшее некоторого фиксированного значения 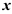
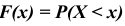
В нашем случае

Таким образом функция распределения 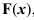 имеет вид:
имеет вид:
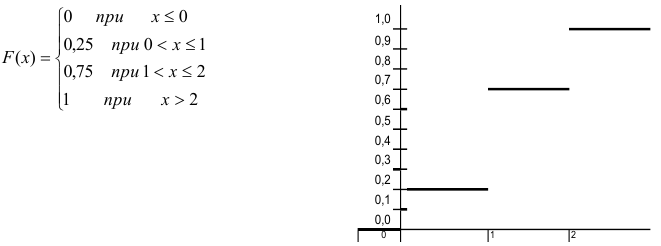
Возможно эти страницы вам будут полезны:
- Решение задач по теории вероятностей
- Помощь по теории вероятности
- Контрольная работа по теории вероятности
- Курсовая работа по теории вероятности
- Решение задач по математической статистике
- Помощь по математической статистике
- Заказать работу по математической статистике
- Контрольная работа по математической статистике
- Курсовая работа по математической статистике
- Теория вероятностей краткий курс для школьников и студентов

