Помощь по математической статистике — решение заданий и задач онлайн

Здравствуйте! Я Людмила Анатольевна Фирмаль, занимаюсь помощью студентам более 17 лет. У меня своя команда грамотных, сильных преподавателей. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И неважно – она по объёму на две формулы или огромная, сложно структурированная, на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.

Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Как получить помощь в выполнении заданий по математической статистике

Вы можете написать сообщение в WhatsApp. После этого я оценю ваш заказ и укажу стоимость и срок выполнения вашей работы. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за вашу работу, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл готовой работы в личные сообщения.

Сколько стоит помощь

Стоимость помощи зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости, загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.

Какой срок выполнения

Минимальный срок выполнения составляет 2-4 дня, но помните, срочные задания оцениваются дороже.

Как оплатить

Сначала пришлите задание, я оценю, после вышлю вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.

Гарантии и исправление ошибок

В течение 1 года с момента получения Вами готового решения действует гарантия. В течении 1 года я и моя команда исправим любые ошибки.

Чуть ниже я предоставила примеры оформления заказов по некоторым темам математической статистики, так я буду оформлять ваши работы если закажите у меня, это не все темы, это лишь маленькая часть их, чтобы вы понимали насколько подробно я оформляю.

Первичная обработка данных

При проведении экспериментов фиксировались значения случайной величины 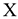, характеризующей время простоя оборудования в ожидании ремонта (в часах).

Пример оформления заказа №1.

Задание: произвести первичную обработку полученных опытных данных с целью изучения свойств случайной величины .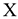

1) Составим расчетную таблицу, в которой запишем вариационный ряд (элементы выборки в порядке возрастания признака) и произведем расчеты, необходимые для вычисления числовых характеристик.

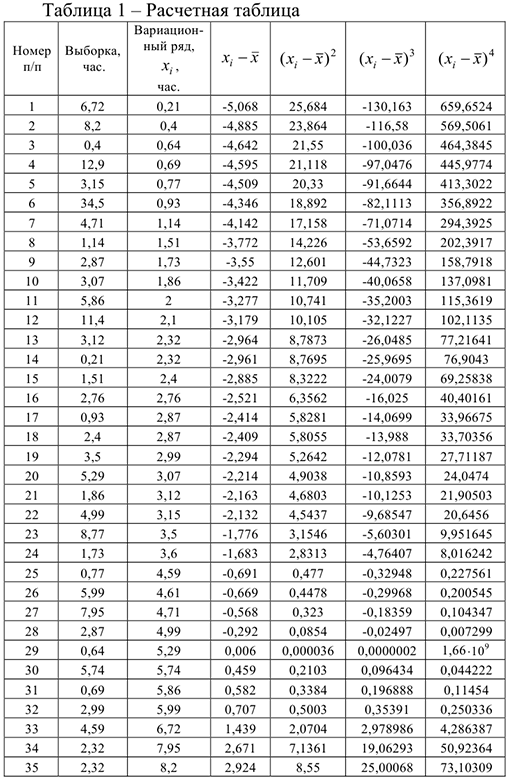
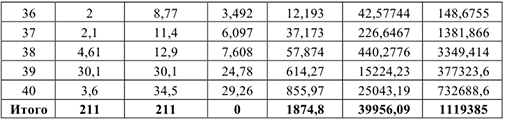
2) Найдем размах выборки

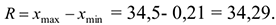
3) Длина интервала

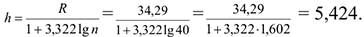
4) границы интервалов:

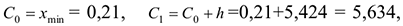
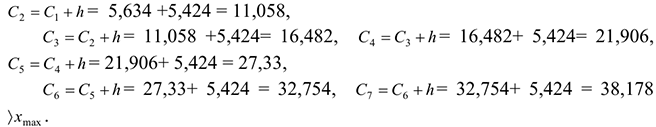
5) Построим интервальный статистический ряд:

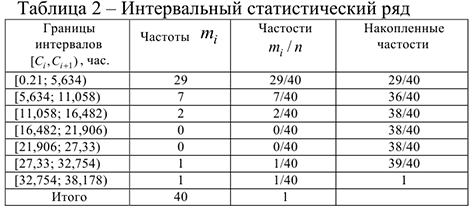
6) Вычислим числовые характеристики.

В качестве оценки математического ожидания используется среднее арифметическое 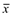наблюденных значений. Эта статистика называется выборочным средним.

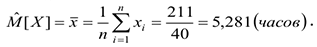
Для оценивания по выборочным данным моды распределения, используется то значение сгруппированного статистического ряда 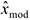, которому соответствует наибольшее значение частоты. По интервальному статистическому ряду определяется модальный интервал, в который попало наибольшее число элементов выборки, и в качестве точечной оценки моды может использоваться среднее значение этого интервала.

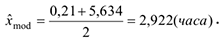
Для определения выборочного значения медианы используется вариационный ряд. В качестве оценки медианы 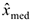принимают средний (т.е. 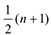-й) член этого ряда, если значение 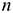— нечётно и среднее арифметическое между двумя средними (т.е. между 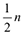-м и 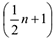-м) членами этого ряда, если — четно. В нашем случае объем выборки = 40 -четное, т.е. в качестве оценки медианы примем

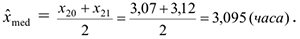
В качестве оценки дисперсии используется статика

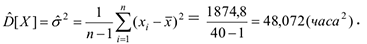
Оценка среднего квадратического отклонения

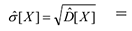
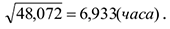
Оценка коэффициента вариации

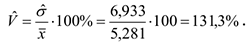
Оценка коэффициента асимметрии

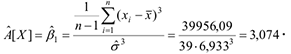
Оценка коэффициента эксцесса

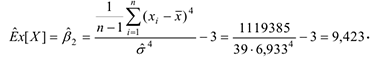
7) Для приближённого построения эмпирической функции распределения воспользуемся соотношением:

8) Построим гистограмму частот и эмпирическую функцию распределения.

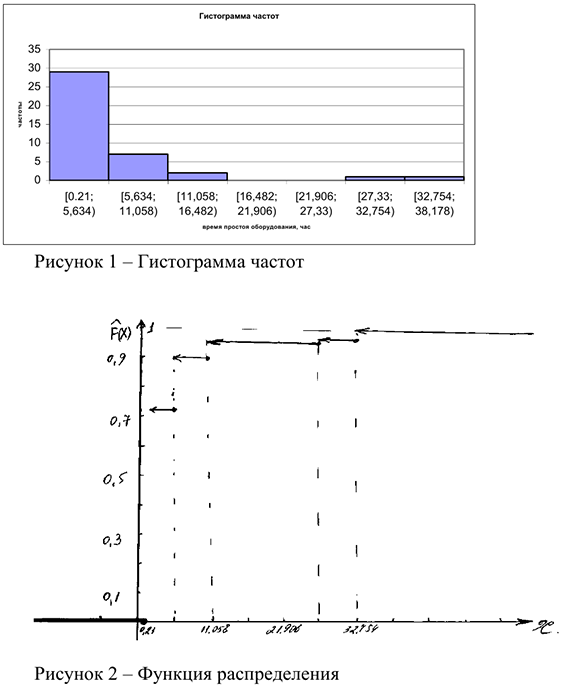
Вывод:

В результате исследования выборки значений непрерывной случайной величины, характеризующей время простоя оборудования в ожидании ремонта, получили следующие результаты, час: минимальное время простоя — 0,21, максимальное- 34,54, среднее значение времени простоя оборудования — 5,28, наиболее вероятное время простоя оборудования — 2,922, средневероятное — 3,095, среднеквадратическое отклонение времени простоя оборудования от среднего значения составило 6,933. Оценка коэффициента вариации составила 131,3%, что указывает на большую колеблемость признака относительно среднего значения, оценка коэффициента асимметрии составила 3,074, оценка коэффициента эксцесса составила 9,423.

Подбор закона распределения одномерной случайной величины

Цель работы изучить методику применения критерия 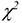Пирсона для проверки гипотезы о виде закона распределения случайной величины.

Пример оформления заказа №2.

Задание: с помощью критерия 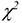проверить согласование выдвинутой гипотезы о виде закона распределения исследуемой случайной величины с имеющимися выборочными данными.

Алгоритм применения критерия 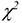для проверки гипотезы о виде закона распределения исследуемой случайной величины.

1 Выборочные данные представляются в виде интервального или сгруппированного статистического ряда.

2 Выбирается уровень значимости .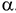

3 Формулируется гипотеза о виде закона распределения исследуемой случайной величины.

4 Вычисляются вероятности 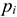, попадания значений случайной величины 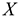в рассматриваемые разряды разбиения:

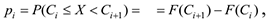
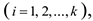
где 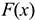— гипотетическая функция распределения случайной величины .

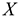Замечание. Если изучается непрерывная случайная величина, то при вычислении значений 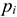необходимо изменить границы первого и последнего частичных интервалов разбиения таким образом, чтобы учесть все возможные значения, которые может принять случайная величина предполагаемого класса. В зависимости от конкретного вида проверяемой гипотезы границы частичных интервалов необходимо изменить следующим образом:

5 Определяются значения теоретических частот 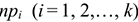. При необходимости для обеспечения условия 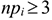(если объем выборки 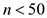) , 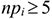(если объем выборки 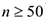) , объединяются несколько соседних разрядов разбиения.

6 Вычисляется наблюдаемое значение критерия :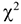

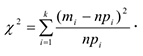
7 По таблицам квантилей распределения 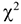определяется критическое значение 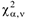соответствующее заданному уровню значимости 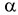и числу степеней свободы .

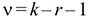Если расчётное значение критерия попадает в критическую область, т. е. 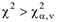то проверяемая гипотеза отвергается (при этом вероятность отклонения верной гипотезы равна ).

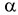В случаях, когда наблюденное значение 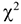не превышает критического 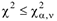считают, что выдвинутая гипотеза не противоречит опытным данным. Подчеркнем, что полученный результат свидетельствует лишь о приемлемом согласовании проверяемой гипотезы с имеющимися выборочными данными и, в общем случае, не является доказательством истинности этой гипотезы.

Пример оформления заказа №3.

По таблице, полученной в задании №1 и по гистограмме частот выдвигаем нулевую гипотезу о виде закона распределения случайной величины 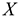(времени простоя оборудования в ожидании ремонта).

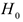: Случайная величина 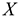(время простоя оборудования в ожидании ремонта) распределена по показательному (экспоненциальному) закону.

Выбираем уровень значимости 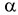=0,05.

Вычислим вероятности 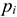, попадания значений случайной величины 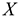в рассматриваемые разряды разбиения по формуле:

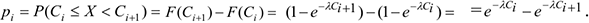
Проверим гипотезу 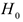с помощью критерия согласия Хи-квадрат Пирсона .

Вычислим параметр

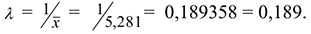
Так как изучается непрерывная случайная величина, то при вычислении значений 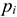необходимо изменить границы первого и последнего частичных интервалов разбиения.

В нашем случае проверяется гипотеза о показательном законе распределения.

Вычислим вероятности по формуле

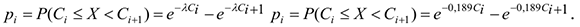
Пример расчета:

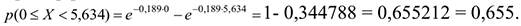
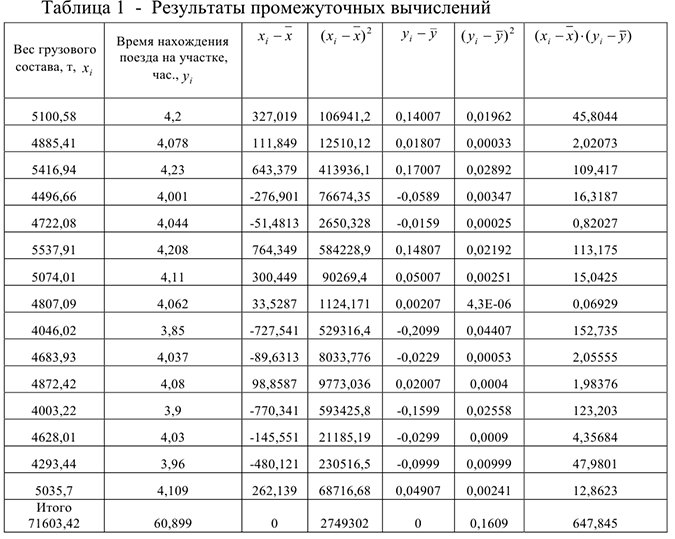
Для того, чтобы облегчить расчеты, можно с помощью пакета программ 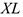выполнить промежуточные расчеты, которые необходимо оформить в виде таблицы:

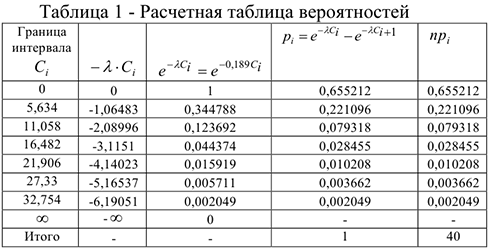
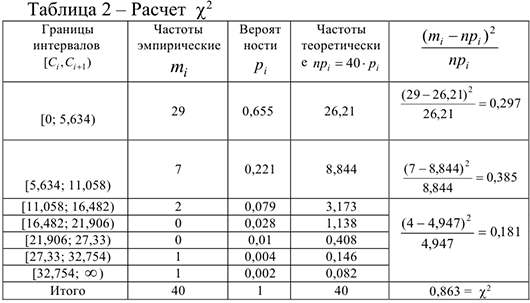
Вычислим число степеней свободы

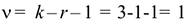
где 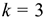— число интервалов в таблице 2 после объединения, 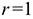— число параметров выбранного закона распределения — в нашем случае показательный закон (один параметр ).

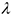По таблицам квантилей распределения 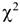определяется критическое значение 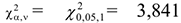, соответствующее заданному уровню значимости 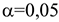и числу степеней свободы .

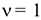Вывод:

Сравниваем полученное значение в таблице 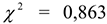с табличным 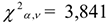. Так как расчетное 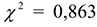меньше, чем табличное 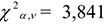, то гипотеза о показательном законе распределения подтвердилась.

Пример оформления заказа №4.

При проведении экспериментов фиксировались значения случайной величины 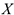, характеризующей цены на зимнюю обувь (в у.е.).

Задание: произвести первичную обработку полученных опытных данных с целью изучения свойств случайной величины 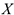, построить гистограмму частот. По гистограмме частот выдвинуть нулевую гипотезу о виде закона распределения случайной величины 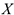и проверить ее с помощью критерия согласия Пирсона.

1) Составим расчетную таблицу, в которой запишем вариационный ряд (элементы выборки в порядке возрастания признака) и произведем расчеты, необходимые для вычисления числовых характеристик.

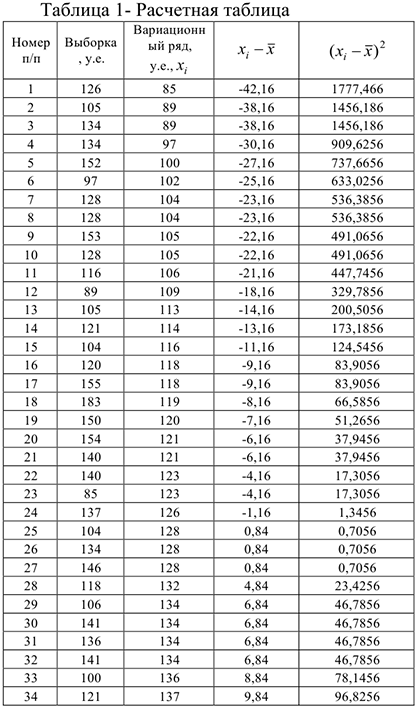
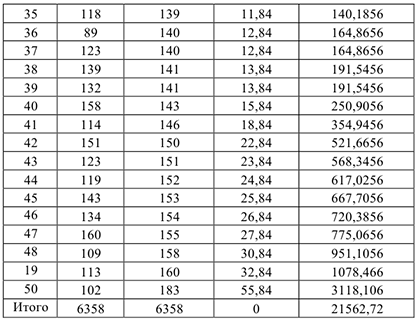
2) Вычислим числовые характеристики.

Выборочное среднее:

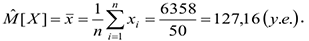
Мода:

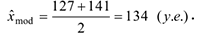
Медиана:

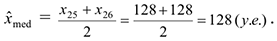
В качестве оценки дисперсии используется статистика

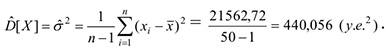
Оценка среднего квадратического отклонения

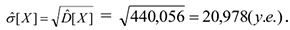
Оценка коэффициента вариации

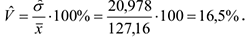
Найдем размах выборки

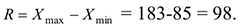
3) Вычислим длину интервала

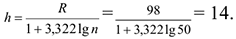
4) Границы интервалов:

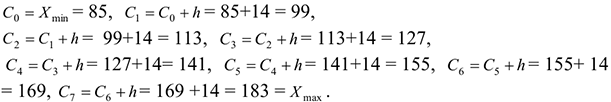
Построим гистограмму частот.

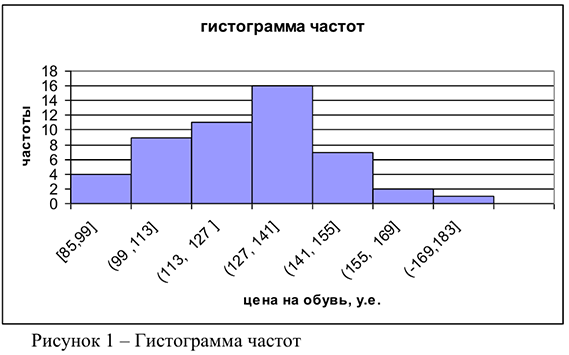
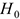: Случайная величина 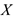(цены на товары (в у.е.)) распределена по нормальному закону.

Выбираем уровень значимости .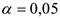

Так как изучается непрерывная случайная величина, то при вычислении значений 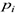необходимо изменить границы первого и последнего частичных интервалов разбиения. В нашем случае проверяется гипотеза о нормальном законе распределения.

Вычислим вероятности 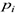попадания значений случайной величины 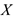в рассматриваемые разряды разбиения по формуле:

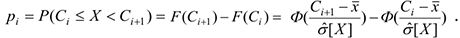
Проверим гипотезу с помощью критерия согласия Хи-квадрат Пирсона . Вычислим параметр

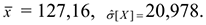
Вычислим вероятности по формуле

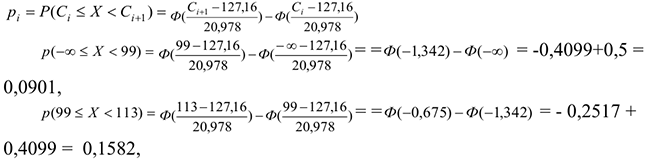
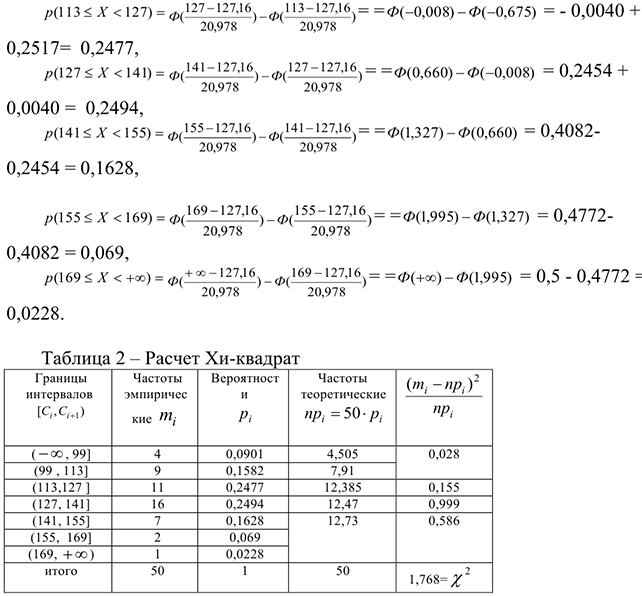
Вывод:

По таблицам квантилей распределения определяется критическое значение 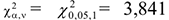, соответствующее заданному уровню значимости 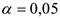и числу степеней свободы 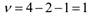.Сравниваем полученное значение 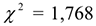с табличным значением 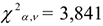. Так как расчетное 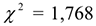меньше, чем табличное 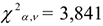, то гипотеза о нормальном законе распределения подтвердилась .

Построение интервальных оценок параметров распределения

Цель работы: изучить методику построения интервальных оценок параметров распределения вероятностей случайной величины.

Задание: построить интервальные оценки математического ожидания и дисперсии исследуемой случайной величины.

Пример оформления заказа №5.

При проведении экспериментов фиксировались значения случайной величины 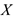, характеризующей цены на зимнюю обувь (в у.е.). В результате вычислений, проведенных в задании № 1, были получены следующие числовые характеристики:

выборочное среднее:

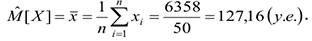
Оценка среднего квадратического отклонения

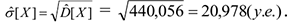
Объем выборки составил 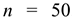. Требуется с доверительной вероятностью 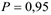определить интервальную оценку:

а) для средней цены на зимнюю обувь;

б) для дисперсии цены на зимнюю обувь;

в) для среднего квадратического отклонения цены на зимнюю обувь. Решение, а) Средняя цена на обувь характеризуется генеральной средней 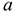. Требуется найти интервальную оценку 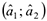параметра 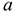с доверительной вероятностью .

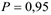Применяем формулу

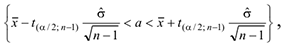
где

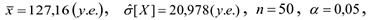
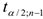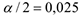
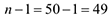
значение определяем по таблицам распределения Стьюдента для 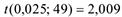. Подставим найденные значения в формулу:

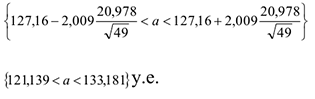
Таким образом, с вероятностью 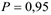можно гарантировать, что средняя цена зимней обуви находится в пределах:

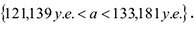
б ) определим интервальную оценку для дисперсии цены на зимнюю обувь.

Интервальная оценка дисперсии

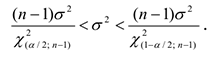
По таблице процентных точек 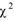-распределения (см. приложение Г) найдем

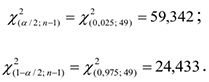
Следовательно,

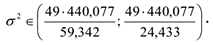
Значит с доверительной вероятностью 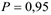можно утверждать, что истинное значение дисперсии будет находиться в интервале

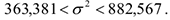
в) С доверительной вероятностью 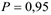можно утверждать, что истинное значение среднего квадратического отклонения 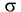будет находиться в интервале

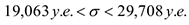
Пример порядка выполнения заданий

1 В задании № 1 вы выполнили обработку статистических данных и вычислили точечную оценку 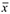среднего значения исследуемой случайной величины 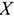и точечную оценку о среднего квадратического отклонения 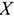. Перепишите из лабораторной работы № 1 значения величин 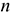, 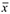и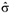

2 Постройте вручную интервальные оценки для неизвестных истинных значени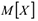й и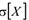

3 Вычислите интервальные оценки для 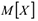и 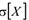на ЭВМ..

4 Сделайте вывод.

Построение регрессионной модели системы двух случайных величин

Цель работы: изучить основные методы регрессионного и корреляционного анализа; исследовать зависимость между двумя случайными величинами, заданными выборками.

Задание: по виду корреляционного поля сделать предположение о форме регрессионной зависимости между двумя случайными величинами; используя метод наименьших квадратов, найти параметры уравнения регрессии; оценить качество описания зависимости полученным уравнением регрессии.

Пример оформления заказа №6.

По результатам пятнадцати совместных измерений веса грузового поезда, т, и соответствующего времени нахождения поезда на участке 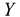, ч, представленных в таблице 1, следует исследовать зависимость между данными величинами. Необходимо определить коэффициенты уравнения регрессии методом наименьших квадратов, оценить тесноту связи между величинами, проверить значимость коэффициента корреляции и спрогнозировать время нахождения поезда на участке при заданном весе поезда (5200 т).

Решение:

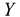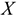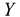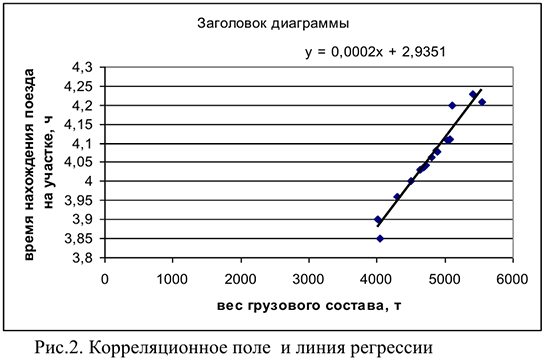
На величину времени нахождения поезда на участке , помимо веса , влияние оказывает профиль и качество железнодорожного полотна, качество подвижного состава, направление и скорость ветра и другие факторы. Поэтому зависимость между величиной времени нахождения поезда на участке и веса поезда 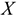является статистической: при одном весе поезда при различных дополнительных условиях время нахождения поезда на участке может принимать различные значения. Для определения вида регрессионной зависимости построим корреляционное поле.

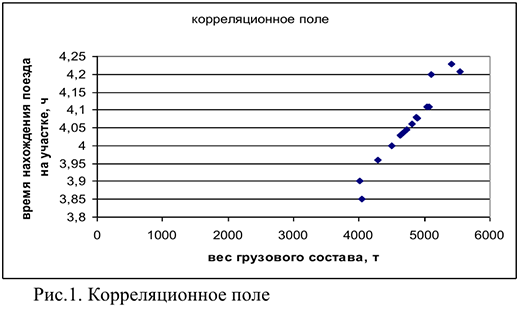
Характер расположения точек на диаграмме рассеяния позволяет сделать предположение о линейной регрессионной зависимости

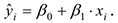
Найдем уравнение прямой линии методом наименьших квадратов.

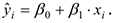
Средний вес грузового состава:

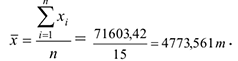
Среднее значение времени нахождения поезда на участке:

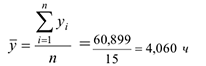
Коэффициенты уравнения:

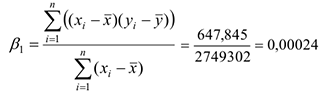
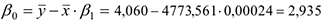
Уравнение регрессии имеет вид :

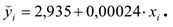
Для линейной связи коэффициенты:

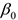— постоянная регрессии, показывает точку пересечения прямой с осью ординат

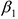— коэффициент регрессии, показывает меру зависимости переменных 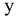от 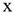, указывает среднюю величину изменения переменной 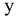при изменении 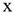на одну единицу, знак 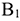определяет направление этого изменения .

Вычислим линейный коэффициент корреляции

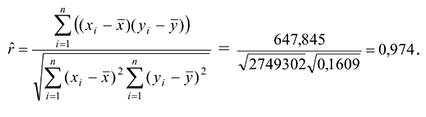
Спрогнозируем время нахождения поезда на участке при заданном весе грузового состава (5200 т).

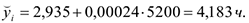
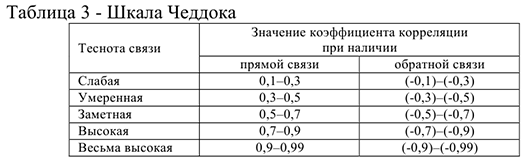
Качественная оценка тесноты связи между величинами выявляется по шкале Чеддока (таблица 3).

Вывод:

Линейный коэффициент корреляции характеризует тесноту связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости. Т.к. 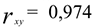, то можно говорить о том, что между величинам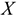и и 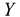существует линейная прямая, весьма высокая связь.

Чтобы сделать статистический вывод о значимости коэффициента корреляции (при проверке линейности регрессионной зависимости) выдвигается нулевая гипотеза об отсутствии линейной зависимости между исследуемыми с. в. против альтернативной гипотезы о наличии линейной связи.

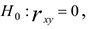
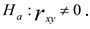
Если гипотеза 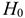отклоняется, то считается, что уравнение регрессии 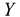по 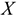действительно имеет линейный вид .

Для проверки гипотезы Но вычисляется 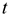-статистика

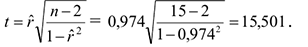
При условии справедливости гипотезы 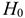рассчитанная 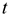-статистика имеет распределение Стьюдента с 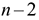степенями свободы. Найденное значение 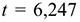сравнивается с критическим значением 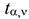при 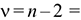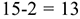степенях свободы (приложение Д). В нашем случае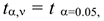 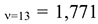. Так как расчетное значение 15,501 по абсолютной величине превосходит табличное 1,771 для заданного уровня значимости, то нулевая гипотеза 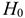о линейной независимости двух с. в. отклоняется.

Характер расположения точек на диаграмме рассеяния позволяет сделать предположение о параболической регрессионной зависимости

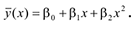
Оценки параметров 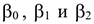найдем методом наименьших квадратов. Для этого составим функцию 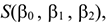которая в случае параболической регрессии примет вид

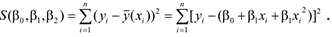
Для отыскания оценок параметров 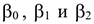, минимизирующих функцию 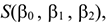составим и решим систему нормальных уравнений :

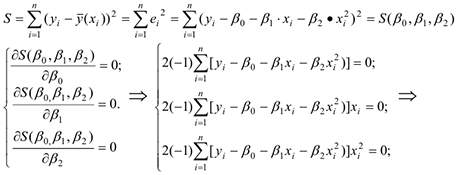
Разделим обе части уравнений (1,2,3) на (-2)

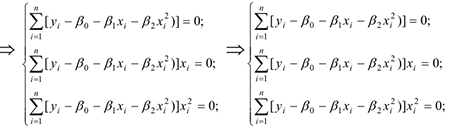
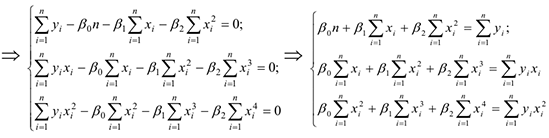
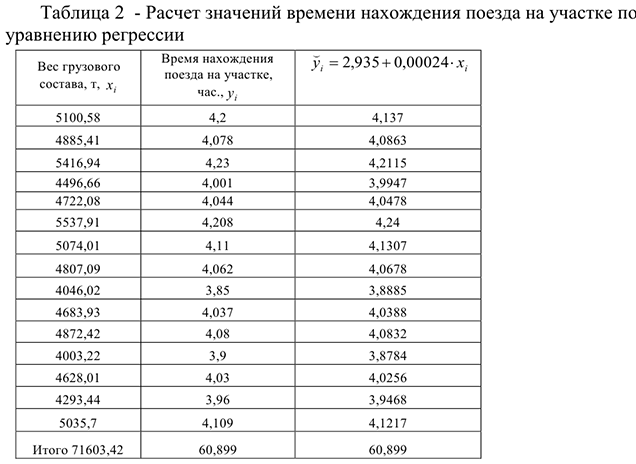
Для вычисления значений сумм, входящих в систему уравнений , составим расчетную таблицу 4.

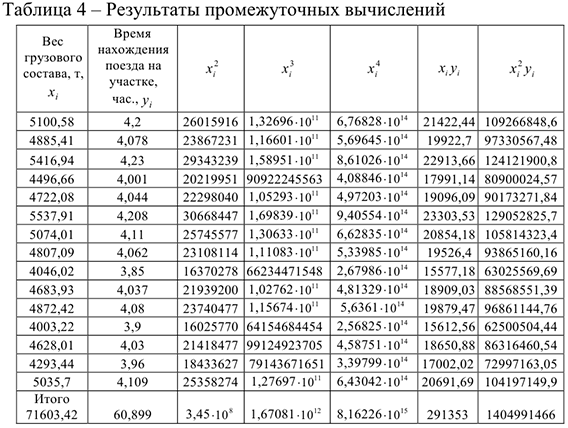
После подстановки значений система уравнений примет вид:

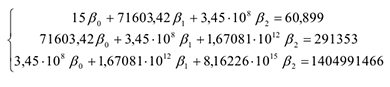
Решив систему уравнений известными методами (методом Крамера, методом Гаусса, методом обратной матрицы) или с помощью MAthCAD, получим следующее решение:

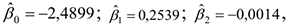
а уравнение регрессии примет вид

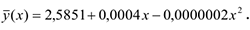
На рисунке представлена диаграмма рассеяния случайных величин 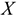и 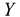с нанесённой линией регрессии.

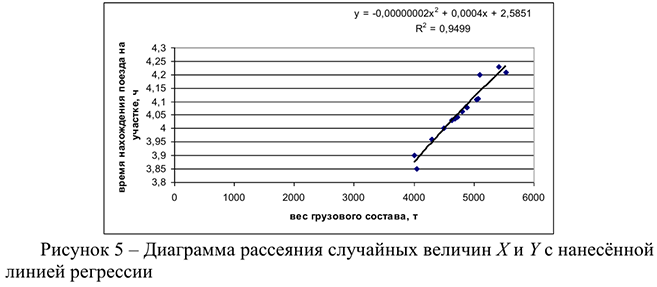
Оценим качество описания зависимости между величиной временем нахождения поезда на участке (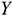) и весом грузового состава (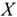) полученным уравнением регрессии с помощью коэффициента детерминации, где 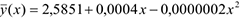— значение времени нахождения поезда на участке, предсказываемое уравнением регрессии, при среднем весе грузового состава 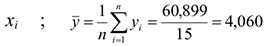час. — среднеарифметическое наблюденных значений времени нахождения поезда на участке.

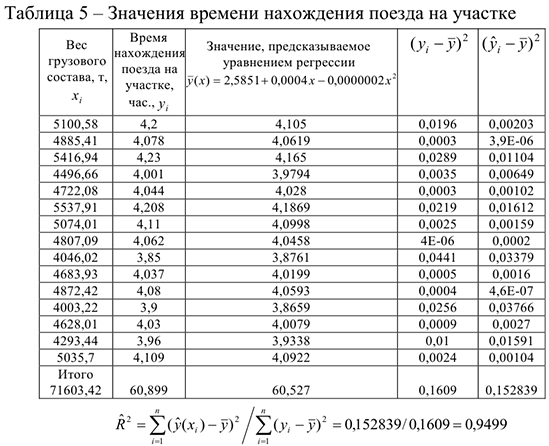
Расчётное значение коэффициента детерминации 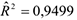указывает на удовлетворительность описания зависимости между величиной веса грузового состава (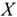) и времени нахождения поезда на участке (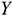), выбранным уравнением регрессии.

Проверим, однако, значимость оценки коэффициента детерминации с помощью статистики Фишера

Проверка значимости 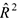. При выполнении процедуры проверки значимости оценки коэффициента детерминации выдвигается нулевая гипотеза о том, что предложенное уравнение регрессии никак не отражает реальную зависимость между с. в., т. е. 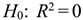. Альтернативная гипотеза заключается в том, что выбранная модель зависимости (уравнение регрессии) 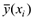в достаточной степени объясняет действительную зависимость между случайными величинами, т. е. .

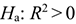Для проверки значимости оценки коэффициента детерминации используется статистика

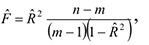
имеющая 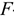-распределение Фишера с 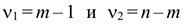степенями свободы. Здесь 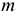— число неизвестных параметров предполагаемого уравнения регрессии. Значение статистики 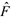сравнивается с критическим значением 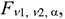найденным по таблицам квантилей распределения Фишера (приложение Е) при заданном уровне значимости и соответствующем числе степеней свободы.

Если 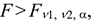то нулевая гипотеза отклоняется, вычисленный коэффициент детерминации значимо отличается от нуля, и с вероятностью ошибки 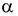можно утверждать, что между исследуемыми величинами существует зависимость предложенного вида, и полученное уравнение регрессии может использоваться в дальнейших исследованиях.

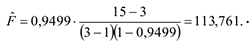
Вывод.:

Критическое значение статистики Фишера для степеней свободы 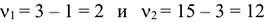и уровня значимости 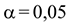составляет 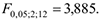. Поскольку расчётное значение статистики Фишера больше критического 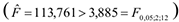, то вычисленный коэффициент детерминации значимо отличается от нуля, и выбранное уравнение регрессионной зависимости между величинами скорости и временем нахождения поезда на участке.

Например, при весе грузового состава 6500 т можно ожидать в среднем время нахождения поезда на участке 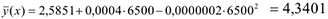час.

Возможно эти страницы вам будут полезны:

• Предмет теория вероятностей и математическая статистика Решение задач по теории вероятностей
• Помощь по теории вероятности
• Заказать работу по теории вероятности
• Контрольная работа по теории вероятности
• Курсовая работа по теории вероятности
• Решение задач по математической статистике
• Заказать работу по математической статистике
• Контрольная работа по математической статистике
• Курсовая работа по математической статистике
• Теория вероятностей краткий курс для школьников и студентов