Если в уравнениях (9.2), (9.3) каждую из функций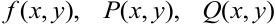 
можно представить в виде произведения двух функций, каждая из которых зависит только от одной переменной 
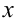или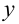 
, то такие уравнения называют уравнениями с разделяющимися переменными.
Уравнения могут быть записаны в формах:
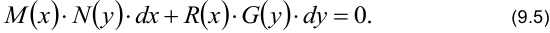
Умножая уравнения (9.4), (9.5) на подходящее выражение, можно добиться разделения переменных (знаками =, +, -) и решения его путём интегрирования.
Пример:
Решить уравнение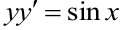 
.
Решение:
Уравнение приводится к виду (9.4) делением обеих частей на 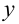, поэтому это уравнение с разделяющимися переменными. Записав производную через отношение дифференциалов, разделим переменные: 
, 
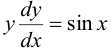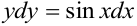. Из равенства дифференциалов следует равенство первообразных с точностью до произвольной постоянной. Интегрируем левую и правую части равенства.
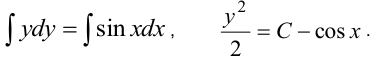
Последнее выражение — общее решение уравнения в неявной форме.
Примечание — общее решение уравнения, полученное в неявном виде, называют ещё общим интегралом уравнения.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Основные определения о дифференциальных уравнениях |
| Дифференциальные уравнения первого порядка |
| Линейные уравнения первого порядка |
| Задача Коши для уравнения 1-го порядка |
