Уравнения плоскости в пространстве: определение и пример с решением по высшей математике

Оглавление:

В пространстве с заданной декартовой системой координат однозначное расположение плоскости можно задать различными способами, соответственно существуют различные уравнения плоскости в пространстве.

1. Уравнение плоскости, проходящей через три заданные точки

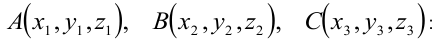
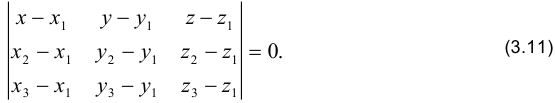
Здесь 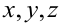Уравнения плоскости в пространстве — текущие координаты точки плоскости.

2. Уравнение плоскости, проходящей через заданную точку 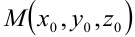перпендикулярно заданному вектору :

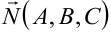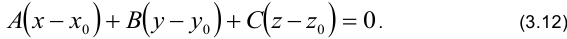
3. Если в уравнении (3.12) раскрыть скобки и обозначить свободный член через 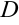, получим общее уравнение плоскости:

Если в общем уравнении (3.13) один из коэффициентов 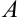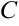Уравнения плоскости в пространстве , , равен нулю, то плоскость проходит параллельно соответствующей оси. Если два коэффициента из 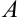, , 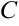равны нулю, плоскость параллельна одной из координатной плоскости. Например, плоскость 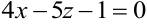Уравнения плоскости в пространстве проходит параллельно оси 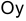, плоскость 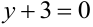проходит параллельно координатной плоскости 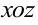через точку 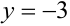на оси .

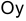Коэффициенты 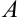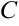Уравнения плоскости в пространстве , , в общем уравнении являются одновременно компонентами вектора, перпендикулярного плоскости.

4. Разделив уравнение (3.13) на (-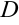), получим уравнение плоскости в отрезках:

Здесь 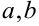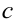Уравнения плоскости в пространстве — отрезки, отсекаемые плоскостью на осях координат. Например, плоскость

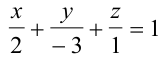
пересекает оси координат в точках 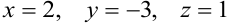Уравнения плоскости в пространстве .

Расстояние 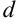Уравнения плоскости в пространстве от точки 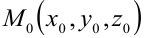до плоскости 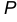, заданной уравнением (3.13), определяется по формуле:

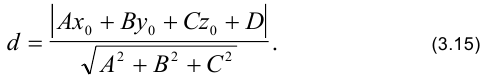
Две плоскости перпендикулярны (параллельны) друг другу, если перпендикулярны (параллельны) их векторы нормали. Поэтому, если даны две плоскости

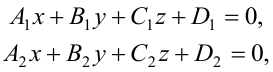
то условие перпендикулярности плоскостей:

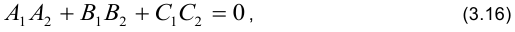
условие параллельности плоскостей:

Пример выполнения задания

Пример:

Даны четыре точки 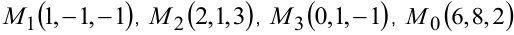Уравнения плоскости в пространстве .

Требуется: а) написать уравнение плоскости, проходящей через точки 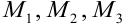Уравнения плоскости в пространстве ; б) преобразовать полученное уравнение плоскости 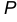в уравнение плоскости в отрезках и построить её; в) найти расстояние 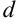от точки 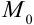Уравнения плоскости в пространстве до плоскости .

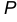Решение:

а) Подставим координаты точек 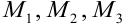Уравнения плоскости в пространстве в уравнение (3.11):

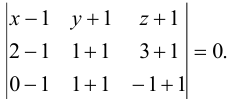
Раскрыв определитель, получим:

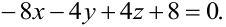
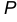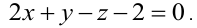
Разделим на (-4) и получим окончательное общее уравнение искомой плоскости Уравнения плоскости в пространстве :

б) Перенеся свободный член в правую часть и разделив на него уравнение, получим уравнение плоскости в отрезках:

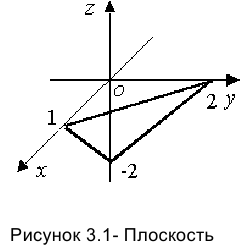
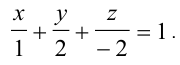
Откладываем отрезки 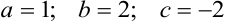Уравнения плоскости в пространстве на осях 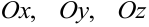соответственно и строим плоскость 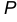(см. рисунок 3.1).

в) Расстояние 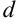Уравнения плоскости в пространстве от точки 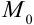до плоскости 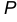найдём по формуле (3.15):

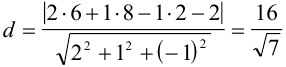Уравнения плоскости в пространстве (ед. длины).

Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:

Высшая математика для 1 курса

Возможно вам будут полезны эти страницы:

Смешанное произведение трёх векторов: определение и пример с решением

Уравнения прямой линии на плоскости

Эллипс, гипербола, парабола

Предел бесконечной числовой последовательности