Уравнение касательной в точке 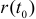 , уравнение нормальной плоскости, проходящей через
, уравнение нормальной плоскости, проходящей через 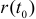 и кривизна кривой
и кривизна кривой 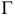 в точке
в точке 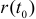 , заданной векторно-параметрическим уравнением
, заданной векторно-параметрическим уравнением
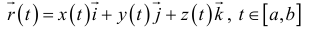
Касательный вектор к кривой 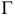 в точке
в точке 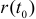 определяется по формуле
определяется по формуле 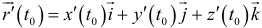 . Предполагается, что
. Предполагается, что 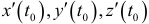 существуют и одновременно не равны нулю. Тогда искомые уравнения касательной имеют вид
существуют и одновременно не равны нулю. Тогда искомые уравнения касательной имеют вид
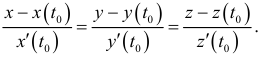
Соответственно уравнение нормальной плоскости имеет вид
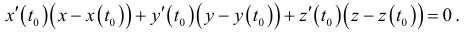
Кривизна кривой 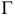 в точке
в точке 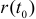 есть величина
есть величина 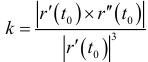 .
.
Пример:
Найти уравнение касательной, уравнение нормальной плоскости и вычислить кривизну линии 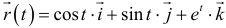 в точке
в точке 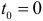 .
.
Решение:
Вычисления дают 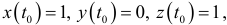
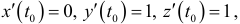
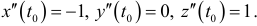
Искомые уравнения касательной 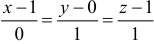 . Искомое уравнение нормальной плоскости
. Искомое уравнение нормальной плоскости 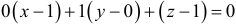 , то есть
, то есть 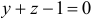 . Найдем числитель в формуле для кривизны
. Найдем числитель в формуле для кривизны 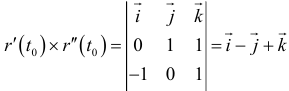 . Длина этого вектора равна
. Длина этого вектора равна 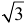 . Длина вектора
. Длина вектора 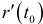 равна
равна 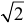 . Подставляя эти значения в формулу для кривизны, получим
. Подставляя эти значения в формулу для кривизны, получим 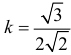 .
.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:

