Если требуется найти неопределенный интеграл от функции, содержащей 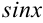 и
и 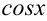 , которые связаны только операциями сложения, вычитания, умножения или деления, то можно использовать универсальную тригонометрическую подстановку.
, которые связаны только операциями сложения, вычитания, умножения или деления, то можно использовать универсальную тригонометрическую подстановку.
Суть этой подстановки заключается в том, что 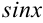 и
и 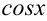 можно выразить через тангенс половинного угла следующим образом:
можно выразить через тангенс половинного угла следующим образом: 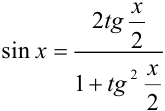 ,
, 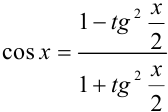 . Тогда, если ввести подстановку
. Тогда, если ввести подстановку 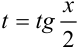 , то
, то 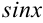 и
и 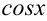 будут выражены через
будут выражены через 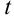 следующим образом:
следующим образом: 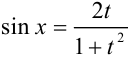 ,
, 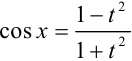 . Осталось выразить
. Осталось выразить 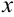 через
через 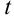 и найти
и найти 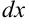 .
.
Если 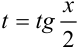 , то
, то 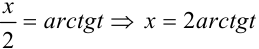 . Найдем
. Найдем 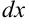 :
: 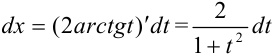 .
.
Итак, для применения универсальной подстановки достаточно обозначить 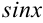 и
и 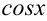 через
через 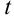 (формулы выделены в рамке), a
(формулы выделены в рамке), a 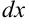 записать как
записать как 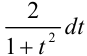 . В итоге под знаком интеграла должна получиться рациональная функция, интегрирование которой рассматривалось в пункте 1. Обычно метод применения универсальной подстановки весьма громоздкий, но он всегда приводит к результату.
. В итоге под знаком интеграла должна получиться рациональная функция, интегрирование которой рассматривалось в пункте 1. Обычно метод применения универсальной подстановки весьма громоздкий, но он всегда приводит к результату.
Рассмотрим пример применения универсальной тригонометрической подстановки.
Пример №20.6.
Найдите интеграл 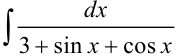 .
.
Решение:
Применим универсальную подстановку 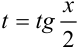 , тогда
, тогда 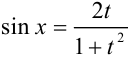 ,
, 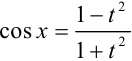 ,
, 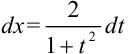 . Следовательно,
. Следовательно,
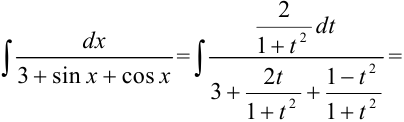
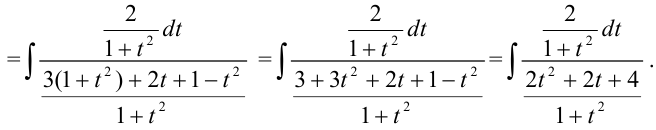
Заменив дробную черту знаком «:», получим: 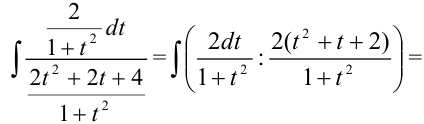
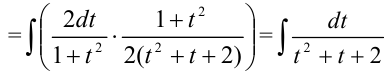 . Этот интеграл решается выделением в знаменателе полного квадрата. Для этого
. Этот интеграл решается выделением в знаменателе полного квадрата. Для этого 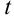 представляем как удвоенное произведение
представляем как удвоенное произведение 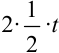 . Тогда к выражению
. Тогда к выражению 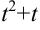 следует добавить квадрат одной второй
следует добавить квадрат одной второй 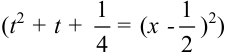 и вычесть его.
и вычесть его.
Получим цепочку преобразований:
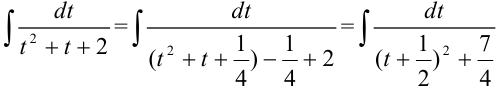 .
.
Вычислим полученный интеграл методом подстановки. Положим 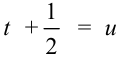 , тогда
, тогда 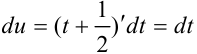 . Подставим
. Подставим  ,
, 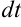 в
в
полученный интеграл: 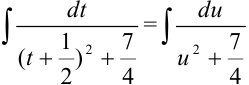 . Воспользуемся табличным интегралом:
. Воспользуемся табличным интегралом: 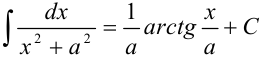 , где
, где 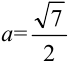 . Тогда
. Тогда 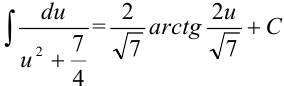 . Поскольку
. Поскольку 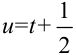 , то
, то 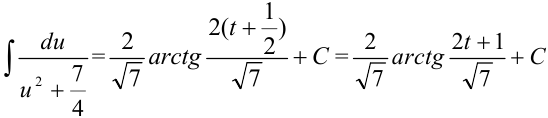 . И, наконец, возвращаемся к переменной
. И, наконец, возвращаемся к переменной 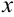 :
: 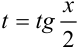 . Получим, что
. Получим, что 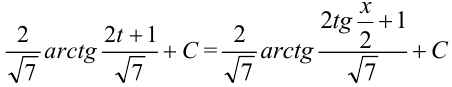 .
.
Ответ: 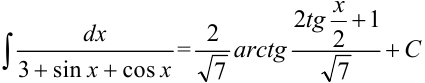 .
.
Еще раз хочется отметить, что задача нахождения неопределенных интегралов от различных функций очень сложна. И хотя всякая непрерывная функция имеет первообразную (а, следовательно, и неопределенный интеграл), среди всего многообразия неопределенных интегралов лишь малая толика выражается через элементарные функции (говорят, такие интегралы «берутся»).
Существует множество интегралов, которые называют «неберущимися». Такие интегралы не выражаются через привычные нам элементарные функции. Так, например, нельзя взять интеграл 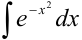 , т.к. не существует элементарной функции, производная которой была бы равна
, т.к. не существует элементарной функции, производная которой была бы равна 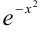 . Но некоторые из «неберущихся» интегралов имеют большое прикладное значение. Так интеграл
. Но некоторые из «неберущихся» интегралов имеют большое прикладное значение. Так интеграл 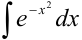 называют интегралом Пуассона и широко применяют в теории вероятностей.
называют интегралом Пуассона и широко применяют в теории вероятностей.
Существуют и другие важные «неберущиеся» интегралы: 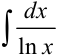 — интегральный логарифм (применяется в теории чисел),
— интегральный логарифм (применяется в теории чисел), 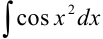 и
и 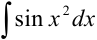 — интегралы Френеля (применяются в физике). Для них составлены подробные таблицы значений при различных значениях аргумента
— интегралы Френеля (применяются в физике). Для них составлены подробные таблицы значений при различных значениях аргумента 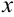 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Интегрирование простейших рациональных дробей. |
| Интегрирование некоторых иррациональных функций. |
| Понятие определенного интеграла. |
| Основные свойства определенного интеграла. |

