Свойства непрерывных функций
Теорема 4.1. Если функции 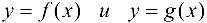 непрерывны в точке
непрерывны в точке 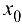 , то функции
, то функции 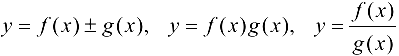
(при условии 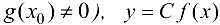 (С — постоянная) непрерывны в точке
(С — постоянная) непрерывны в точке 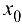 .
.
Доказательство следует из определения непрерывности функции и аналогичных свойств пределов функции.
Например, если 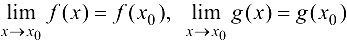 , то
, то
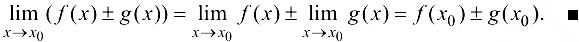
Замечание 4.1. Теорема справедлива и при любом конечном числе непрерывных функций.
Теорема 4.2 (Вейерштрасса). Функция 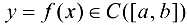 ограничена на данном отрезке.
ограничена на данном отрезке.
Доказательство. От противного.
Предположим, что функция 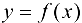 не ограничена на отрезке
не ограничена на отрезке 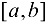 . Тогда для любого
. Тогда для любого 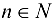 найдется точка
найдется точка 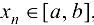 , такая, что
, такая, что 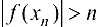 .
.
Известно, что из ограниченной последовательности 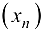
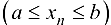 можно выделить сходящуюся подпоследовательность
можно выделить сходящуюся подпоследовательность 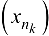 , для которой
, для которой 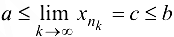 (теорема 2.4 Больцано-Вейерштрасса). Тогда, с одной стороны,
(теорема 2.4 Больцано-Вейерштрасса). Тогда, с одной стороны, 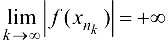 — в силу неограниченности
— в силу неограниченности 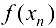 с другой стороны,
с другой стороны, 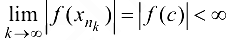 — в силу непрерывности функции
— в силу непрерывности функции 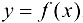 .
.
Получено противоречие. ■
Теорема 4.3 (Вейерштрасса)*. Функция 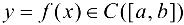 достигает на этом отрезке своих точной верхней и точной нижней граней.
достигает на этом отрезке своих точной верхней и точной нижней граней.
Напомним, что точная верхняя грань М непрерывной на отрезке 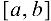 функции
функции 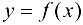 называется максимумом функции на этом отрезке:
называется максимумом функции на этом отрезке: 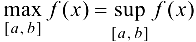 ; точная нижняя грань m — минимумом функции па этом отрезке:
; точная нижняя грань m — минимумом функции па этом отрезке: 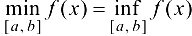 . Напомним, также, что нулем функции
. Напомним, также, что нулем функции 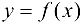 называется всякое значение
называется всякое значение 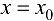 , при котором
, при котором 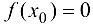 .
.
Теорема 4.4 (Коши о нулях функции). Если функция 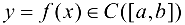 и на концах данного отрезка принимает значения разных знаков, то внутри отрезка найдется, по крайней мере, одна точка
и на концах данного отрезка принимает значения разных знаков, то внутри отрезка найдется, по крайней мере, одна точка 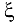 , такая, что
, такая, что 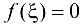 .
.
Доказательство.
Пусть, для определенности, .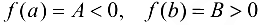 .
.
Разделим отрезок 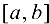 точкой
точкой 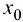 пополам. Тогда если
пополам. Тогда если 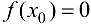 , то искомая точка
, то искомая точка 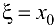 найдена и теорема доказана. Если
найдена и теорема доказана. Если 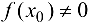 , то возьмем ту половину
, то возьмем ту половину 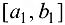 отрезка
отрезка 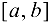 для которой
для которой 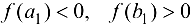 . Разделим отрезок
. Разделим отрезок 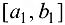 точкой
точкой 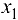 пополам. Если
пополам. Если 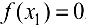 , то искомая точка
, то искомая точка 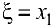 найдена и теорема доказана. Если
найдена и теорема доказана. Если 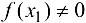 , то возьмем ту половину
, то возьмем ту половину 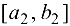 отрезка
отрезка 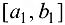 , для которой
, для которой 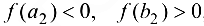 , и выполним очередное разбиение. Продолжив эти рассуждения, получим, что, либо через конечное число шагов найдется точка
, и выполним очередное разбиение. Продолжив эти рассуждения, получим, что, либо через конечное число шагов найдется точка 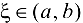 для которой
для которой 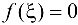 , либо существует конечная последовательность вложенных стягивающихся отрезков
, либо существует конечная последовательность вложенных стягивающихся отрезков 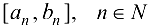 , для которых
, для которых 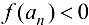
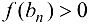 . Согласно теореме 2.5 (Кантора) существует единственная точка
. Согласно теореме 2.5 (Кантора) существует единственная точка 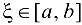 общая для всех отрезков, причем
общая для всех отрезков, причем 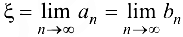
Учитывая непрерывность функции 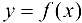 и переходя к пределу в неравенствах
и переходя к пределу в неравенствах 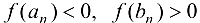 , получим
, получим
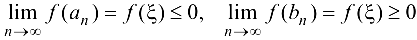
откуда
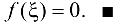
Теорема 4.5 (Коши о промежуточном значении). Если функция 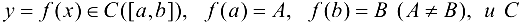 — любое число, заключенное между А и В. то найдется точка
— любое число, заключенное между А и В. то найдется точка 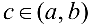 , в которой
, в которой 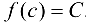 .
.
Доказательство.
Пусть, для определенности, 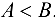 . Тогда для функции
. Тогда для функции 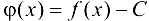 имеем
имеем

Итак, функция 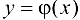 на концах отрезка
на концах отрезка 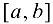 имеет разные знаки. Согласно теореме 4.4 существует точка
имеет разные знаки. Согласно теореме 4.4 существует точка 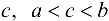 , такая, что
, такая, что 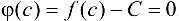 . Следовательно,
. Следовательно, 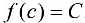 . ■
. ■
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:

