Оглавление:
Свойства градиента
- Производная в точке по направлению вектора
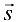имеет наибольшее значение, если направление вектора 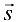совпадает с направлением градиента. Это наибольшее значение производной равно 
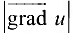(следует непосредственно из равенства (19.2)). - Производная по направлению вектора, перпендикулярного к вектору
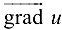, равна пулю (следует из равенства (19.2) при 
).
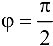Определение 19.3. Точка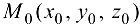 
, в которой 
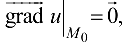называется особой для скалярного поля; в противном случае — обыкновенной (неособой).
Теорема 19.2*. Во всякой неособой точке плоского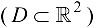 
скалярного поля градиент поля направлен по нормали к линии уровня, проходящей через эту точку, в сторону возрастания поля.
Пример 19.1.
Найти скорость и направление наибыстрейшего возрастания функции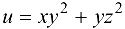 
в точке 
.
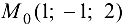Решение:
Направление наибыстрейшего возрастания функции в точке совпадает с направлением градиента, а его скорость равна значению длины градиента в этой точке.
Найдем градиент функции в общем виде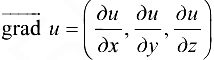 
.
В данном случае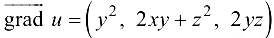 
. В точке 
: 
.
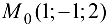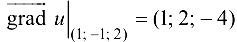Скорость возрастания составит:
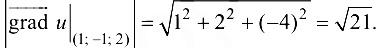
Ответ: направление наибыстрейшего возрастания функции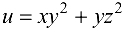 
в точке 
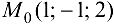задается вектором 
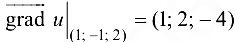, а его скорость составляет 
.
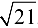Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
