Оглавление:






Способ вращения вокруг прямой уровня (способ совмещения)
- Прямой метод поворота уровня (загрузка комбинации) 1. Точка вращения. Рассмотрим поворот точки А вокруг горизонта. Точка A, вращающаяся вокруг горизонтали A, представляет собой окружность в плоскости 2, которая перпендикулярна оси вращения h. Поскольку эта плоскость является плоскостью, которая проецируется горизонтально, Рисунок 109.
- Проецируется на плоскость проекции P в виде прямой линии 2i, перпендикулярной проекции h. Для упрощения рисунка 109 и чертежа плоскость проекции P зафиксирована на горизонтальном уровне h. Поэтому круг, который рисует точка A при вращении, проецируется на плоскость проекции nt в форме отрезка прямой линии. В плоскости P2 этот круг проецируется как эллипс.
«Потому что он в плоскости 2 наклонен относительно плоскости P2. Людмила Фирмаль
Если вы поставили цель ограничить вращение точки A и найти только выравнивание с горизонтальной плоскостью G, нарисованной на горизонтальном уровне h, вы можете легко настроить A, определив радиус вращения r точки L. Фактически, проекция А, совмещение А точки А размещается в проекции 2 на расстоянии, равном радиусу поворота r точки А от проекции О, центра вращения О.
Фактическое значение радиуса поворота r можно определить методом прямоугольного треугольника. Следовательно, прямоугольный треугольник / 4 / 4,0 (рис. 109, а) радиусом поворота r является гипотенуза, а ножки этого треугольника — горизонтальная проекция O, / 4, радиус поворота r и относительная высота h относительно точки А соответственно. = AAt. Горизонтальная плоскость Г.
Рисунки 109 и б показывают, как построить сложный чертеж. Найдите горизонтальную проекцию O и центр вращения O на пересечении 21 и A, которая рисует линию 2, проходящую через ось проекции точки A Используя прямые треугольники 0, / 4, / 4 *, ножка O, / 4 представляет собой горизонтальную проекцию радиуса поворота точки.
Найти естественное значение радиуса поворота r точки A, используя A, и высоту h точки A относительно ножки AtA * -плоскости G. Поместив линию 2 i из точки O, естественный размер радиуса поворота r представляет собой горизонтальную проекцию A желаемой комбинации A. На фиг.109b также показана структура переднего выступа 02 центра вращения, переднего выступа 02A2 радиуса вращения и переднего выступа A2 выравнивания A.
На фиг. Однако эти конструкции передней проекции часто не нужны и не показаны на чертеже. Поворот точек вокруг передней части выполняется аналогичным образом. 2. Плоское вращение. Затем рассмотрите возможность вращения плоскости вокруг прямого уровня, пока она не совпадет с плоскостью уровня.
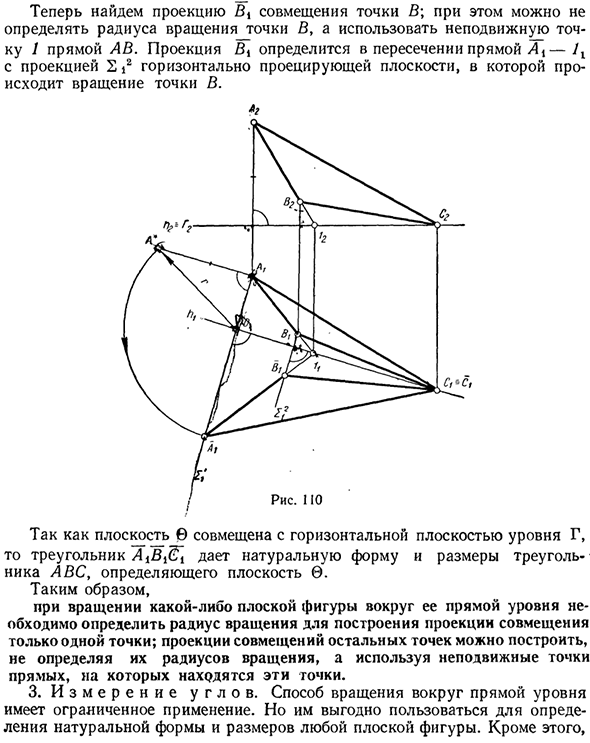
Цель такой комбинации — определить естественную форму и размер фигуры, помещенной в совместимую плоскость, или наоборот, построить на этой плоскости фигуры до заданной формы и размера. это. Вам необходимо повернуть плоскость 0 (ABC) в общем положении, пока она не выровняется с частью горизонтальной плоскости (Рисунок 110).
Рисует горизонтальную h, проходящую через точку C в указанной плоскости. Выбор этой горизонтали в качестве оси вращения имеет два преимущества. Во-первых, точка C фиксируется во время вращения. Следовательно, C == C, а во-вторых, проекция> 4,5,01 выравнивания не перекрывается с проекцией / 1,5, С. Определите проекцию / 4 и соедините точку A с плоскостью Γ, проходящей через горизонталь h.
- Для этого проведите линию 2 l_Lft через точку 2 ^ и поместите ее из точки 0 в естественное значение радиуса r. Это предварительно определяется с использованием прямоугольного треугольника OII *. Теперь найдите проекцию Bx для выравнивания точки B. В этом случае вместо определения радиуса поворота точки B можно использовать фиксированную точку 1 линии AB.
Поскольку плоскость © выровнена с горизонтальной плоскостью уровня Γ, треугольник AXB ^ представляет естественную форму и размеры треугольника ABC, определяющего плоскость 6. Вот так Если вы поворачиваете плоскую фигуру вокруг ее непосредственного уровня, вам нужно определить радиус поворота, чтобы построить проекцию, которая объединяет только одну точку.
Проекция Bx определяется пересечением линии 2 и проекции 2 * на горизонтальной плоскости проекции, где точка B вращается. Людмила Фирмаль
Проекции для других комбинаций точек могут быть построены без определения их радиуса поворота, но с использованием фиксированных точек линии, где эти точки расположены. 3. Измерение угла. Использование методов вращения вокруг линейных уровней ограничено. Тем не менее, полезно использовать его для определения естественной формы и размера плана этажа.
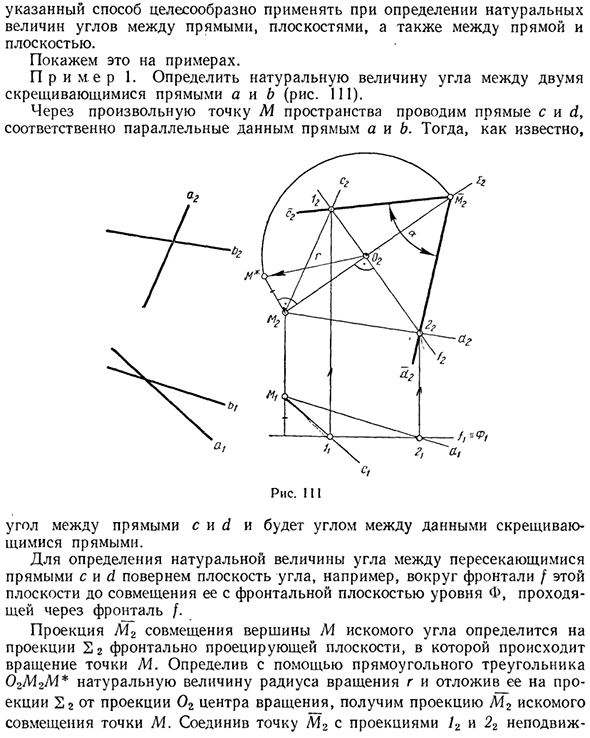
Кроме этого Рекомендуется применять этот метод при определении естественного значения угла между линиями, между плоскостями и между линиями и плоскостями. Это показано в качестве примера. Пример 1. Определите естественное значение угла между двумя пересекающимися линиями a и b (рисунок 111). Рисует линии c и d параллельно указанным линиям a и b, соответственно, через любую точку M в пространстве.
И, как вы знаете, Рисунок болезни Угол между линиями заканчивается и становится углом между указанными линиями пересечения. Чтобы определить естественное значение угла между пересекающимися линиями c и d, плоскость угла, например, вокруг передней части этой плоскости, а также передней части уровня, через который она проходит через флортал / Поверните до выравнивания.
Проекция M2 желаемого угла выравнивания вершины M определяется проекцией 22 плоскости передней проекции, вокруг которой вращается точка M. Используйте прямоугольный треугольник OGM2M * для определения естественного значения радиуса поворота r, установите центр вращения выступа 2r из выступа 02r и получите выступ M2 желаемой точки выравнивания M.
Точка M2 и выступ 1d и Исправь 22 и подключи Найти проекцию комбинации c2, d2 точек, линий c и d. Угол a между линиями c2 и d2 определяет естественное значение требуемого угла между линиями c и d или то же самое между линиями a и b. Пример 2. Определить естественное значение двугранного угла, образованного плоскостями (ABC) и Л (а || b) (рис. 112).
Если задано двугранное ребро, естественное значение этого угла можно определить, заменив плоскость проекции, сделав ребро линией проекции (§22). Рис. 113 Рисунок 112 В этом случае, как и во многих других случаях, двугранный край на чертеже не определен, и вам не нужно его находить. Другими словами, нет необходимости строить прямую линию на пересечении этих плоскостей.
Фактически, если мы рисуем перпендикуляры nx и l2 из любой точки пространства M в плоскости b и A, мы получим два плоских угла a и (5 в точке M в плоскости этих перпендикуляров. Как только естественное значение угла между вертикальными плоскостями n1 и n2, соответственно равного прямому углу смежных двугранных углов, определяется вращением вокруг линейного уровня (см. Пример 1), без построения двугранного края Решите проблему.
Пример 3. Определите естественное значение угла a, образованного прямой линией / плоскостью 0 (рис. 113). Если нормаль n к плоскости 0 понижена от точки M линии и точки K и L пересечения линии / или плоскости 0 соединены, то угол MKL между линией / и его проекцией KL на плоскость 0 желателен Угол равен.
Однако выполнение этих структур на сложных чертежах вносит ненужную сложность, поскольку должно найти точку К. Этого можно избежать, определив естественное значение угла KML между линией I и вертикалью n. Этот угол дополняет желаемый угол ~ 90 °. Поэтому после определения естественного значения угла 0 он вращается вокруг прямой. Уровень (см. Пример 1) остается дополнить его под прямым углом.
Это дополнение дает естественное значение для желаемого угла a. 4. Рассмотрим пример применения метода вращения вокруг прямой линии для построения общего положения в конкретной плоскости перед конкретной диаграммой. Пример. Он образует правильный шестиугольник с плоскостью b, определяемой пересекающимися линиями f и m, стороны которого равны a и центрированы в определенной точке O (02) (рис. 114).
Сначала включите Dan-Ul / L ^ T 1J 4 Горизонтальный ч ЛЧС /// т ‘до совместимости / Горизонтальный 1 секунда на самолете Г ^^^ Ной за горизонтом. Я строю проект для этого «ч-ч ^ Точка выравнивания Определить радиус поворота точки г М и М Правым треугольником QjMtM *. Соединение проекции Mt с проекциями в фиксированных точках 11 и 2 дает проекцию с соответствием u_t {строка / и т. Д.
Проекция выравнивания 0 {Центр окружности O определяется по линии 0, которая параллельна линии m и определяется фиксированной точкой 3. Затем создайте правильный шестиугольник AxBxCxDxEiFu, проекцию желаемого гексагонального расположения, используя окружность с центром в точке Ot и радиусе a.
Обратная конструкция затем возвращает плоскость в исходное положение и сначала находит гексагональную горизонтальную и переднюю проекции. В этом случае, чтобы найти проекцию шестиугольных вершин, мы использовали прямую плоскость 0, параллельную прямой m и определяемую неподвижными точками 3, 4 и 5 горизонтали h. 5.
После рассмотрения основных методов преобразования сложных чертежей и решения различных метрических задач с некоторыми примерами примените этот метод или этот метод для решения конкретной метрической задачи. Вы можете сделать некоторые выводы о достоверности того, что вы делаете.
Очевидно, что При решении задач пространственной метрики рекомендуется использовать метод замены проекционной плоскости. Способ поворота вокруг всех метрических задач и прямой уровень задач, которые могут быть сведены к ним.
Смотрите также:
Примеры решения задач по начертательной геометрии
| Основные задачи, решаемые способом замены плоскостей проекций | Способ дополнительного проецирования |
| Способ вращения вокруг проецирующей прямой | Кривые линии и их проекции |

