Оглавление:






Способ вращения вокруг проецирующей прямой
- Метод поворота вокруг прямой проекции 1. Как уже показано (§20), при применении метода поворота плоскость проекции не изменяется, и изменяется исходное положение в пространстве. Изменение исходного положения осуществляется вращением Он вокруг оси. Линия проекции уровня или прямая линия обычно выбирается в качестве оси вращения.
- Это связано с тем, что структура, выполняемая в сложном чертеже при вращении вокруг этих линий, намного проще, чем структура при вращении вокруг прямой линии в обычном положении. Если вы повернете оригинал вокруг оси, которая является прямой линией в общем положении, сложный чертеж сначала преобразуется так, чтобы эта ось была линией проекции.
После вращения вокруг линии проекции результат возвращается в основную систему плоскости проекции. Людмила Фирмаль
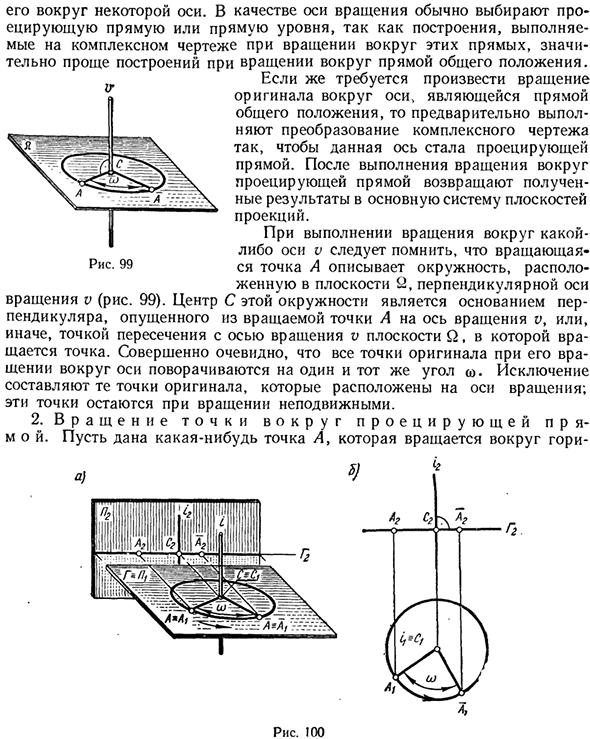
Обратите внимание, что при выполнении вращения вокруг оси v точка вращения A представляет круг в плоскости S2, перпендикулярной оси вращения v (рисунок 99). Центр C этого круга является началом перпендикуляра, опущенного из повернутой точки A на ось вращения v, или же пересечением с осью вращения v плоскости Q, вокруг которой вращается точка.
Совершенно ясно, что все исходные точки вращаются на один угол при повороте вокруг оси. Исключением является исходная точка на оси вращения. Эти точки остаются неподвижными во время вращения. 2. Поверните точку вокруг линии проекции. Дайте точку А, вращающуюся вокруг горы инфракрасный Линия проекции i.
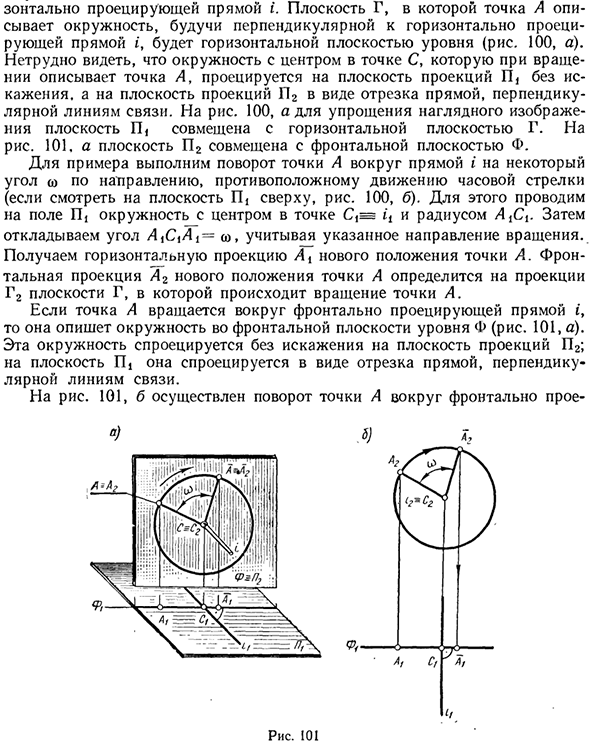
Плоскость Г, в которой точка А, перпендикулярная горизонтальной проекционной линии i, рисует круг, является горизонтальной плоскостью уровня (рис. 100, а). Вы можете видеть, что круг с центром в точке C, представленной точкой A во время вращения, проецируется на плоскость проекции P без искажений. И на плоскости проекции P2 в виде отрезка прямой линии, перпендикулярной линии связи.
Чтобы упростить рисунок 100 и визуальное изображение, объедините плоскость P с горизонтальной плоскостью G. 101 и плоскость P2 совмещены с передней плоскостью F. Например, поверните точку A на угол вокруг линии i в направлении, противоположном движению по часовой стрелке (Рис. 100, b при просмотре плоскости P сверху). Для этого нарисуйте круг в поле P и кружок _ (= оно и радиус AXC {с центром в точке C.
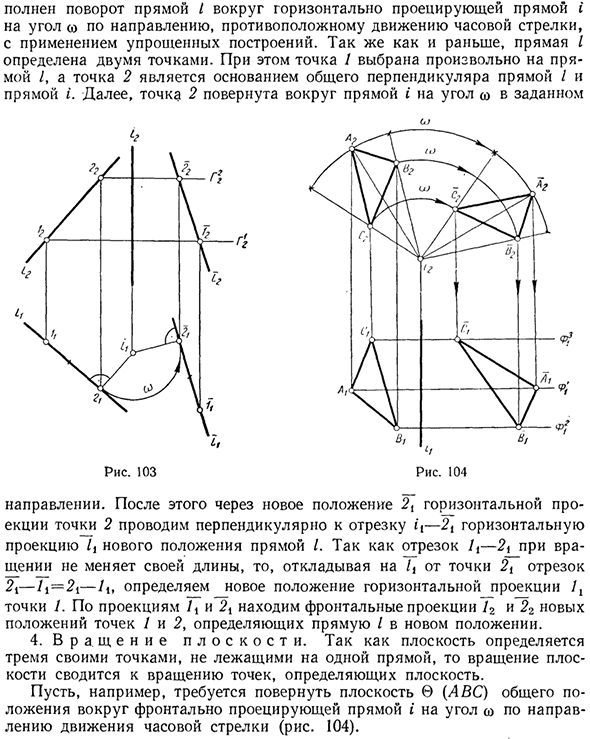
Затем отложите угол / 4 (^ / 4 = рассмотрите указанное направление вращения) Получите горизонтальную проекцию Ax нового местоположения точки A. Местоположение точки A определяется проекцией G2 плоскости G. Если точка A вращается вокруг прямой t, выступающей вперед, нарисуйте круг перед уровнем A (рис. 101, а). Этот круг проецируется без искажения на плоскость проекции P2.
Плоскость P проецируется в виде отрезка прямой линии, перпендикулярной линии связи. Рисунок 101, б, точка А вращается вокруг передней проекции а, с, а, Укажите прямую линию i с углом <o в направлении движения по часовой стрелке. Вот так Когда точка вращается вокруг горизонтальной (передней) линии проекции, горизонтальная (передняя) проекция точки рисует круг, а передняя (горизонтальная) проекция перемещается вдоль прямой линии, перпендикулярной линии связи. 3.
С прямым вращением линии. Поскольку прямая линия определяется двумя точками, вращение линии сводится к вращению точек, которые определяют линию. Например, предположим, что вы хотите повернуть прямую линию в общем положении вокруг прямой линии i, которая выступает в горизонтальном направлении и на угол o »в направлении, противоположном движению по часовой стрелке (рисунок 102).
Выберите две произвольные точки и поверните на оси i вокруг оси i под тем же углом в определенном направлении вращения (в этом случае код 7t должен быть равен коду между точками, помеченными крестиком) Это не должно быть). Новая позиция / и 2 точки / и 2 — это угол (в этом направлении o С учетом треугольников / 1—2t— и / t——, если стороны первого треугольника — r4 __ и 2j — равны сторонам второго треугольника — it и 2 — ix соответственно.
- Угол также равен. так Д / j-2t-it = Д7, -2, -i, следовательно, / 1-21—-2, Вот так. Если вы поворачиваете на один угол вокруг горизонтальной проекционной линии, расстояние между горизонтальными проекциями точек не изменяется. по-видимому При вращении вокруг линии передней проекции расстояние между передними проекциями точек не должно меняться.
Рисунок 103 вы- Рисунок 102 Используя упрощенную структуру, линия / определяется двумя точками, как при полном повороте / предыдущей линии вокруг линии i, выступающей горизонтально на угол o в противоположном направлении по часовой стрелке.
Эти концепции могут несколько упростить построение новых проекций прямых линий, которые вращаются вокруг проектируемой линии. Людмила Фирмаль
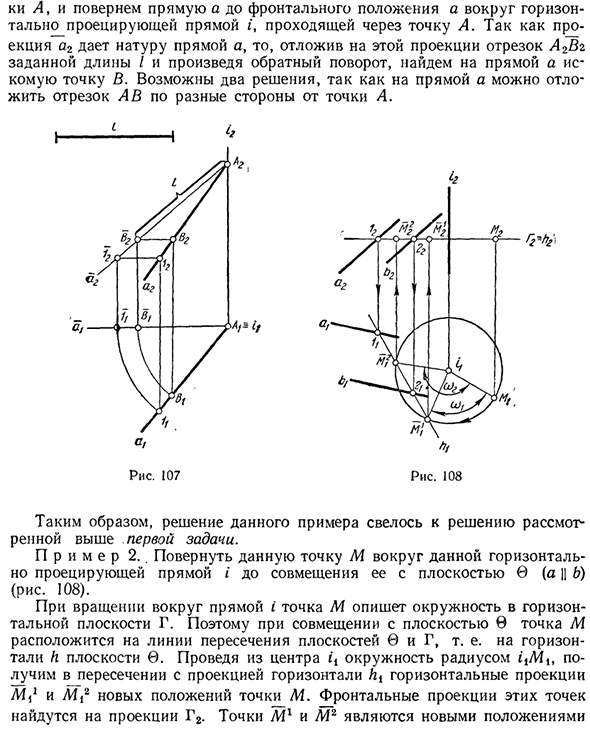
Кроме того, точка 1 произвольно выбрана в строке /, а точка 2 является нормальной ссылкой для линии / и линии i. Затем поверните точку 2 вокруг линии i на угол o. час Рис. 104 Рисунок 103 Направление. Затем он рисует перпендикулярно сегменту через горизонтальную проекцию новой позиции 2, точка 2, горизонтальную проекцию новой позиции линии 2t / j.
Поскольку отрезок lt-2t не меняет свою длину во время вращения, положите точку / сегмент- / = 2i-A из точки 2X, чтобы определить новое положение точки / горизонтальной проекции /. Из проекции / и 2 найдите фронтальную проекцию / 2 и 2d новой позиции точки / и 2. Это определяет строку I на новом месте. 4. Плоское вращение.
Поскольку плоскость определяется тремя точками, которые не находятся на прямой линии, вращение плоскости — это вращение точек, которые определяют плоскость. Например, предположим, что вы хотите повернуть плоскость © (ABC) в общем положении вокруг передней позиции i на угол w (рис. 104). Точки вращения A, B и C, определяющие один и тот же угол на этой плоскости (в определенном направлении вращения o) (в этом случае код A2A2 помечается крестиком между точкой, помеченной штрихом и крестиком.
Должен быть равен код между точками)), новые позиции A, B и C этих точек. Точки «A, B и C» определяют новое положение плоскости после поворота назад вокруг плоскости i на угол o. Поскольку передняя проекция треугольника ABC сохраняет свое значение при вращении вокруг линии прямой проекции I, одна из сторон треугольника может вращаться первой, как показано на рисунке 3. 103, создайте новую позицию для двух вершин треугольника.
Тогда новую позицию третьей вершины можно найти из следующего условия: LА2В2Сг = ЛАгВ2С2 (рис. 104). 5. Вращаясь вокруг линии проекции, вы можете решить все четыре основные проблемы, решаемые в 22, заменив плоскость проекции. Тем не менее, решение этих проблем с помощью метода вращения является более громоздким, чем решение путем замены плоскости проекции.
Таким образом, вместо рассмотрения здесь всех четырех проблем для сравнения показаны только первое и третье решения. Первое задание Поверните прямую I в общем положении в положение уровня прямой. Поверните линию / к предыдущей позиции. Для этого возьмем горизонтально выступающую линию r \, которая проходит через точку / линию / относительно оси вращения (рис. 105).
Выбор этой оси вращения несколько упрощает структуру, потому что точка / является фиксированной, и для вращения линии / остается только одна точка. Например, горизонтальная проекция линии 2 / новой позиции / должна была быть перпендикулярна линии связи, поэтому мы построили проекции 2 и 22 для новой позиции точки 2, поэтому это определяет линию I для передней позиции / вы.
Проекция / 2 — это неискаженная проекция линии /, а угол a между линией / 2 и линией равен Дает естественный угол наклона прямой I к плоскости проекции P, перпендикулярной линии связи Чтобы повернуть прямую линию / в горизонтальное положение, необходимо использовать прямую линию, выступающую перед прямой линией / в качестве оси вращения. Третий вызов. Поверните плоскость (ABC) в общем положении в положение плоскости проекции.
Например, поверните плоскость в положение плоскости, которую вы хотите проецировать на фронт. Для этого вам нужно повернуть вокруг горизонтально выступающей линии i, чтобы часть горизонтали h в плоскости 0 стала выступающей линией (рис. 106). В этом случае горизонтальная проекция h 1 горизонтальной линии h занимает положение / g, параллельное линии связи, поэтому определяют угол поворота. 0) = <(/ 2t, h {).
Теперь, если повернуть этот угол вокруг оси I, проходящей через точки B, A и C, новое положение этих точек A и C и фиксированная точка B определят новое положение прямой проекции этой плоскости. вы. Передняя проекция точки плоскости 0 на новом месте находится на двух прямых линиях @ 2, которые являются передними проекциями плоскости.
Угол a между проекцией B2 и линией, перпендикулярной линии связи, дает естественный угол наклона от плоскости 0 к плоскости G11-. Чтобы повернуть плоскость в положение горизонтальной проекции, в качестве оси вращения следует принять линию прямой проекции, проходящую через точку на плоскости О. В этом случае вам необходимо выполнить поворот так, чтобы фронт плоскости 0 был горизонтальной проекционной линией. 6.
Решите два примера. В первом из этих примеров используется метод поворота для преобразования сложного чертежа, а во втором — его Используется для решения кинематических задач. Пример! Перемещает отрезок A B определенной длины / по прямой a в общее положение из точки A (рис. 107).
В строке a выберите любую точку, отличную от данной точки Рисунок Yubu Поверните ki A и прямую линию a в переднее положение a вокруг горизонтальной линии, которая выступает по прямой линии A. Поскольку проекция a2 дает свойство прямой a, отрезок ArBr длины, заданной этой проекцией, снимается, и вращение меняется на противоположное.
В строке a отрезок L B может быть перенесен на другую сторону точки A, поэтому возможны два решения. Рис. 107 Рис. 108 Следовательно, решение в этом примере было сведено к решению первой проблемы, обсужденному выше. Пример 2. Поверните определенную точку M вокруг определенной горизонтальной проекционной линии i, пока она не совпадет с плоскостью 0 (a || b) (Рисунок 108).
При вращении вокруг линии i точка M представляет окружность в горизонтальной плоскости G. Следовательно, в сочетании с поверхностью 9 точка M находится на пересечении плоскостей B и Γ, то есть на горизонтальной плоскости h плоскости 0. Нарисуйте круг радиуса ixMu из центра i, пересечение горизонтальной проекции ht, горизонтальной проекции M, 1 и Mg2 в новом месте точки M.
Фронтальные проекции этих точек можно найти в проекции Т2. Точки M1 и Mg — новые правила Точка M повернута на i и r на углы соответственно перед выравниванием с плоскостью b. Если проекция hx касается круга, у задачи есть одно решение, и если проекция проходит за пределы круга, у проблемы нет решения.
Смотрите также:
Примеры решения задач по начертательной геометрии
| Основы способа замены плоскостей проекцией | Способ вращения вокруг прямой уровня (способ совмещения) |
| Основные задачи, решаемые способом замены плоскостей проекций | Способ дополнительного проецирования |

