Способ дополнительного проецирования

Способ дополнительного проецирования

• Дополнительные методы НКОКЗИРОНЛИЙН 1. Как уже показано (§20), в дополнение к основным методам преобразования сложных чертежей (метод замены проекционной плоскости и метод вращения), дополнительные методы проекции могут использоваться при решении задач позиционирования Рекомендуется использовать его.

• При использовании этого метода направление проекции и плоскость, на которой выполняется проекция, выбираются в соответствии с требуемым преобразованием чертежа. Поэтому исходная проекция на выбранной плоскости, то есть исходная тень на выбранной плоскости, дополнительно строится на сложном чертеже.

Обычно используется наклонная или центральная проекция на горизонтальной или проекционной поверхности. Людмила Фирмаль

Целью использования дополнительных проекций является получение той или иной исходной вырожденной проекции при решении задачи о местоположении. Как известно, решение проблем с местоположением значительно упрощено. Поскольку решение является более сложным, чем использование базового метода преобразования сложных чертежей, нецелесообразно использовать дополнительные проекции для решения метрических задач. 2.

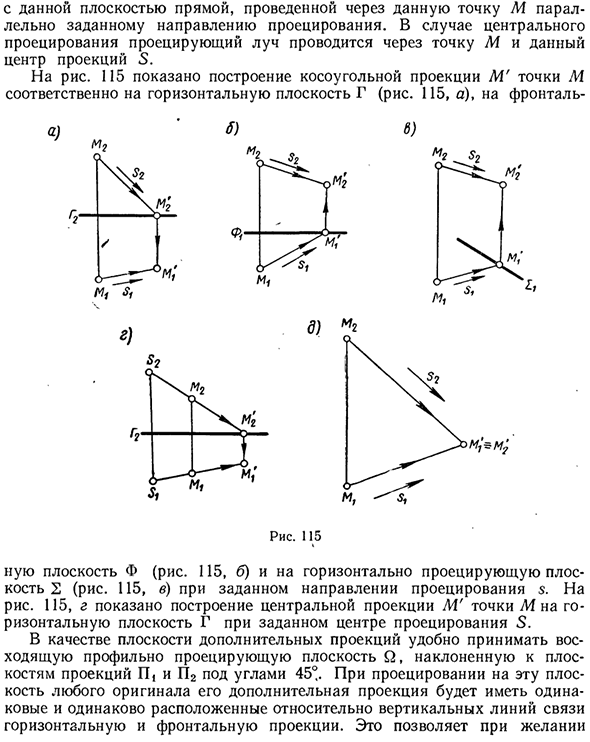
Наклонная проекция M ‘точки M на заданную плоскость для заданного направления s проекции является пересечением. Он имеет заданную плоскость с линией, проходящей через заданную точку M, параллельной заданному направлению проекции. В случае центральной проекции проекционный луч проходит через точку M и центр S этой проекции.

На рисунке 115 показана композиция наклонной проекции M ‘для каждой горизонтальной плоскости Г (рис. 115, а) и передней точки М Направление проекции $ на плоскость Φ (фиг. 115, b) и плоскость 2 (фиг. 115, c) проецируется в горизонтальном направлении. На фиг. 115, d показана конфигурация центрального выступа M ‘точки M на горизонтальной плоскости G для заданного центра выступа 5. На фиг.

В качестве дополнительной плоскости проекции удобно иметь восходящий профиль, который проецирует плоскость Q, наклоненную относительно плоскостей проекции P и P2, под углом 45 °. При проецировании на эту исходную плоскость дополнительные проекции в равной степени располагаются в одном и том же положении относительно горизонтальной линии и вертикальной линии фронтальной проекции.

Это позволяет вам г) м2 Рис. 115 В сложных чертежах объедините горизонтальную проекцию и фронтальную проекцию оригинальной дополнительной проекции. Это обеспечивает известное упрощение в некоторых случаях. На фиг.115e показана конфигурация комбинированной проекции косой проекции M ‘точки M на плоскость Q для заданного направления s проекции.

Легко понять ранее использовавшуюся прямую рефракцию прерывистой линии при решении задач положения с использованием прямых профилей Рисунок 116 Связи можно интерпретировать как комбинированные проекции дополнительных проекций данных линии профиля на плоскость Q. 3. Теперь рассмотрим конструкцию дополнительной косой проекции линий и плоскостей.

В этом случае вы устанавливаете цель для такой структуры и получаете вырожденную проекцию линий и плоскостей. То есть прямая проецируется на точку, а плоскость проецируется на прямую. Предположим, нам нужно создать вырожденную проекцию данной линии a на фронтальную плоскость (рис. 116, а).

Для этого выберите направление проекции s, параллельное линии a, и представьте проекцию линии a точкой a ‘. На рисунках 116 и b показана конфигурация комбинированной проекции. Вырожденная линия проекции а. Чтобы создать вырожденную проекцию плоскости, достаточно выбрать направление проекции s, параллельное указанной плоскости.

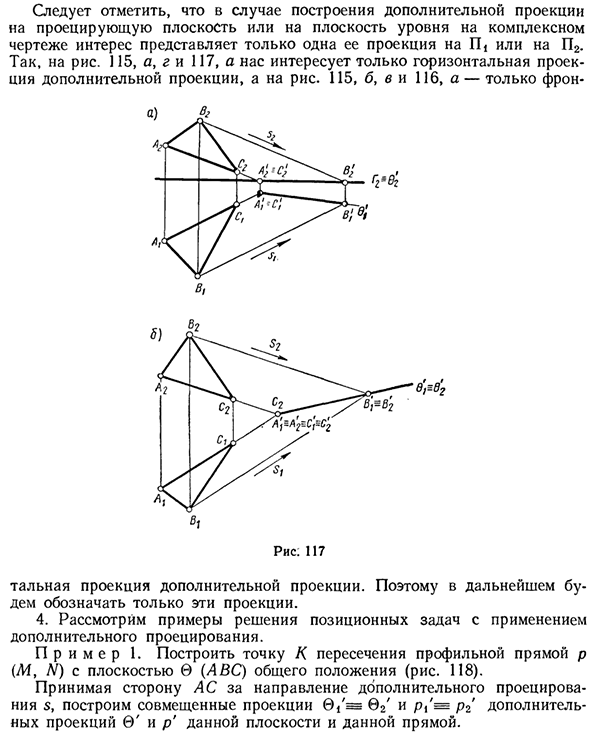
На фиг.117а показана конфигурация проекции плоскости 0 (LAN) на горизонтальную плоскость Γ, а на фиг.11 направление s C> 40 проекции на фиг.1. Сделано Дополнительная проекция этой плоскости — прямая. При создании дополнительных проекций на плоскости проекции сложного чертежа или горизонтальной плоскости учитывается только одна проекция на P или P2.

• Поэтому нас интересует только горизонтальная проекция на рисунках 115a, d, 117 и дополнительные проекции. 115, b, c и 116, только спереди Рис. 117 Общая проекция дополнительных прогнозов. Следовательно, только эти прогнозы будут показаны в будущем. 4. Рассмотрим пример, в котором используются дополнительные проекции для решения проблемы положения.

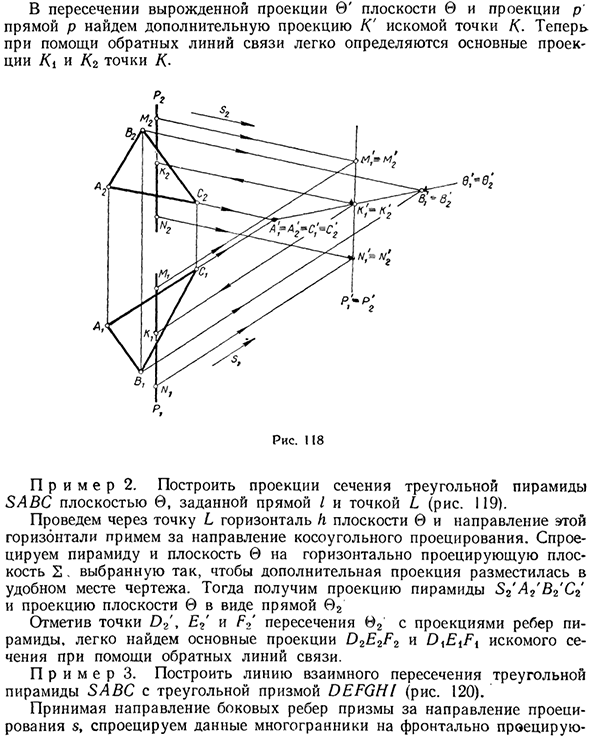
Пример 1. Постройте пересечение K между линией профиля p (M, N) и плоскостью общего положения (ABC) (рис. 118). Постройте эту плоскость с дополнительными выступами 6 / = © 2 ‘и дополнительными выступами pg 0’ и p ‘, используя сторону AC направления дополнительных выступов.

В а) в Найти дополнительную проекцию K ‘для искомой точки K на пересечении вырожденной проекции 0’ на плоскости 0 и проекции p на прямой p. Людмила Фирмаль

Здесь основные выступы Ki и K2 могут быть легко определены с использованием обратной линии связи. Точка К • ERE; Пример 2. Создайте проекцию сечения треугольной пирамиды SABC, заданной линией I и точкой L (рисунок 119). Нарисуйте горизонтальную плоскость 0 плоскости 0, проходящую через точку L, и это горизонтальное направление является направлением наклонной проекции.

Проецирует пирамиду и плоскость 0 на плоскость 2, которая выступает горизонтально. Выберите для размещения дополнительных выступов в удобных местах на чертеже. Далее получаем проекцию пирамиды S2A2B2’C2 и проекцию плоскости 0 в виде линии 02. D2 \ £, чтобы отметить точку?

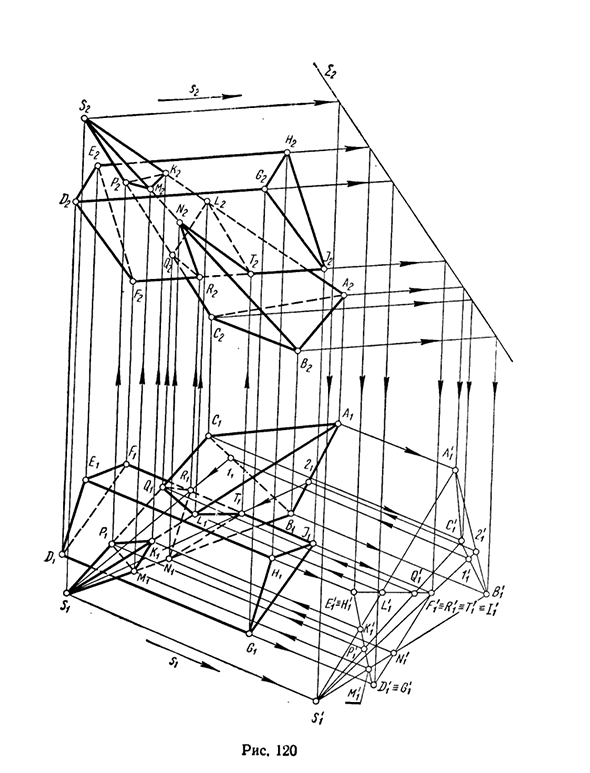
‘И / Н2 и пересечение V проекции края пирамиды, используя обратную линию связи, вы можете легко найти основные проекции D2E2F2 и DxEiFt в нужном сечении. Пример 3. Нарисуйте линию пересечения между треугольной пирамидой SABC и треугольной призмой DEFGHI (Рисунок 120).

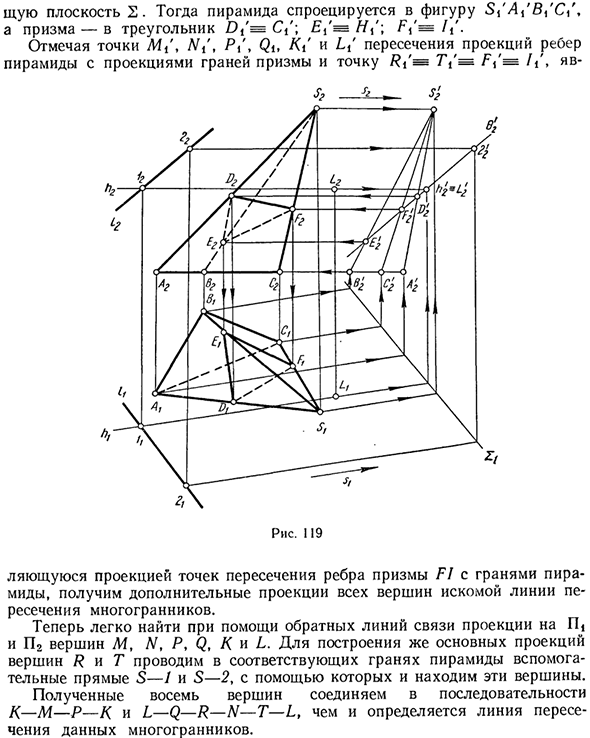
Проецирует эти многогранники на переднюю проекцию с направлением бокового края призмы в качестве направления проекции s. Рисунок 118 Самолет 2. Далее пирамида проецируется на фигуру S \ AX’BX’C \, а призма проецируется на треугольник D / = C /. £, ‘= //,’; / Vs /, ‘. Отметьте точку M /, DO /. I /, Qi, / C / и Lt ‘пересечение проекции края пирамиды и грани призмы и точки Ri =’ 7Y = F% = /, ‘ S? 4-х}

Используйте проекцию пересечения края призмы FI и грани пирамиды, чтобы получить дополнительную проекцию всех вершин искомой линии пересечения многогранника. Теперь вы можете легко найти проекции вершин М, N, Р, Q, К, L П и П2, используя обратную линию связи.

Создать основные проекции вершин R и Т с помощью нахождения 5 этих вершин на соответствующих гранях пирамиды. Получающиеся восемь вершин связаны последовательностями K-M-P-K и L-Q-R-N-T-L, которые определяют линии пересечения этих многогранников.

Смотрите также:

Примеры решения задач по начертательной геометрии

Основные задачи, решаемые способом замены плоскостей проекций	Кривые линии и их проекции
Способ вращения вокруг проецирующей прямой	Образование, задание и изображение поверхностей