Ряды Тейлора и Маклорена
Предположим, что функция 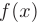 определена и имеет производные всех порядков в окрестности точки
определена и имеет производные всех порядков в окрестности точки  . Тогда она может быть разложена в ряд Тейлора:
. Тогда она может быть разложена в ряд Тейлора:
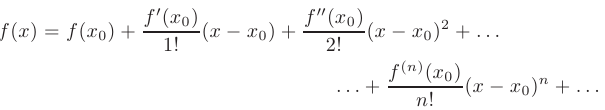
Последнее равенство справедливо лишь в том случае, когда так называемый остаточный член
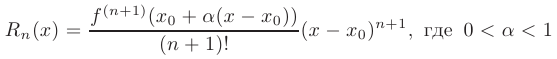
стремится к нулю при  . Если
. Если 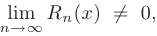 то ряд не представляет данной функции, хотя может и сходиться (к другой функции).
то ряд не представляет данной функции, хотя может и сходиться (к другой функции).
В частном случае при 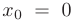 ряд Тейлора называется рядом Маклорена:
ряд Тейлора называется рядом Маклорена:
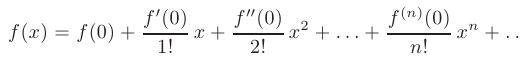
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:

