Оглавление:
Пример №10.
Решить графически следующую ЗЛП:
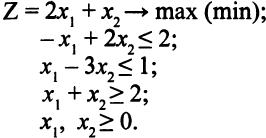
Допустимая область показана на рис. 2.6. Эта область не ограничена. Вектор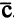 
= (2, 1) указывает направление возрастания целевой функции.
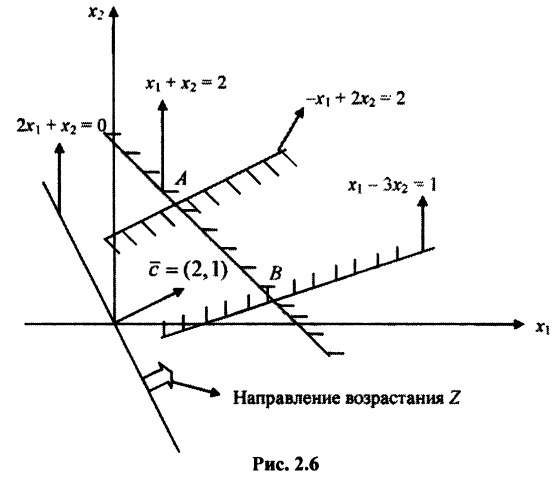
Из рис. 2.6 следует, что линию уровня можно неограниченно перемещать в направлении вектора 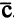= (2,1). При любом значении 
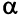прямая 
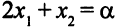пересекает допустимую область. Целевая функция не ограничена сверху в допустимой области, задача максимизации целевой функции не имеет решения. Обозначим эту ситуацию так: 
.
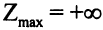Минимум целевой функции достигается в точке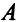 
. Найдем ее координаты. Точка 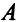лежит на пересечении прямых 
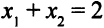и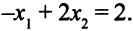 
. Решая систему уравнений
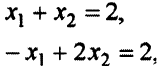
находим:
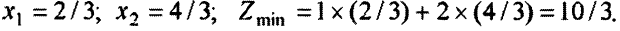
Пример №11.
Решить ЗЛП:
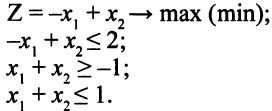
Допустимая область показана на рис. 2.7.
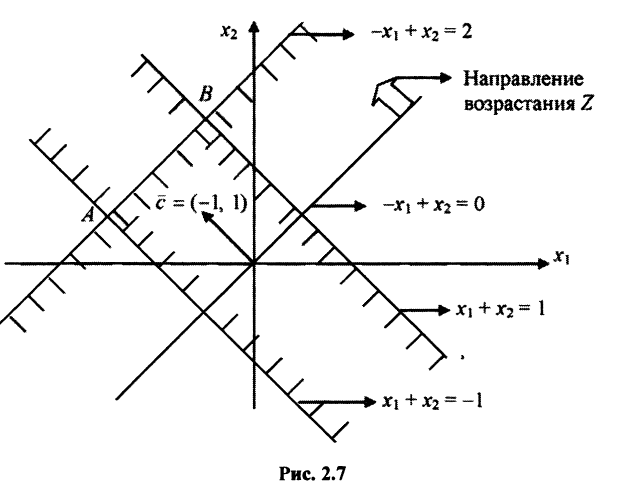
В этом случае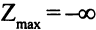 
, целевая функция не ограничена снизу в допустимой области. Максимум целевой функции достигается во всех точках отрезка 
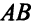. Отрезок 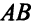принадлежит линии уровня 
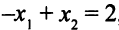, следовательно, 
.
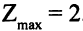Обобщая полученные результаты, можно сказать:
- Допустимая область — это всегда выпуклый многоугольник, даже если она не ограничена.
- Оптимальное решение, если оно существует, — это либо вершина допустимой области, либо множество точек некоторого отрезка допустимой области (но тогда среди них можно выделить две вершины — концы этого отрезка), либо некоторая прямая.
Эта задача взята со страницы решения задач по предмету «линейное программирование»:
Решение задач по линейному программированию
Возможно эти страницы вам будут полезны:
