Оглавление:
Решение дифференциальных уравнений при помощи степенных рядов
Пусть необходимо найти частное решение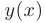 
дифференциального уравнения 2-го порядка, удовлетворяющего начальным условиям:
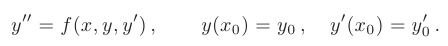
Будем искать решение 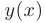в виде ряда Маклорена до 
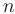-го члена включительно:
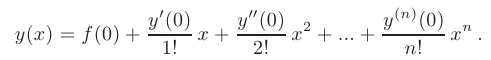
Значения
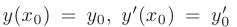
известны, поэтому сразу находится значение
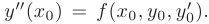
Для нахождения значений следующих коэффициентов степенного ряда необходимо последовательно вычислять производные от выражения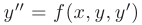 
и подставлять в них уже известные значения предыдущих производных. Так же как и при вычислении определенного интеграла с ростом числа членов, учитываемых в разложении 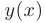, ошибка решения снижается, а точность — возрастает.
Пример 8.9.
Найти три первых отличных от нуля члена разложения в степенной ряд функции, удовлетворяющей решению указанной задачи Коши:
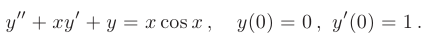
► Будем искать решение уравнения в виде степенного ряда
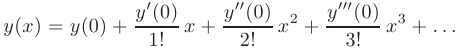
Из начальных условий уже известны значения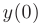 
и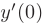 
. Тогда 
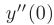можно найти, подставив эти значения в исходное дифференциальное уравнение:
Для нахождения коэффициентов последующих членов ряда продифференцируем исходное уравнение необходимое число раз и вычислим значения полученных производных при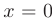 
:
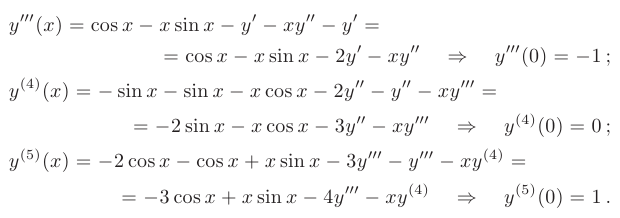
Подставляя найденные значения производных в степенной ряд, получаем искомое частное решение:
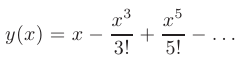
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Ряды Тейлора и Маклорена в математике |
| Вычисление определенных интегралов при помощи степенных рядов |
| Матрица в математике |
| Операции над матрицами в математике |
