Алгебраическое уравнение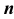 
-ой имеет вид:
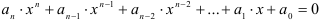, где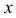 
— неизвестная величина, а 
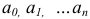— заданные комплексные числа, причем 
.
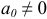В 1799 г. выдающийся немецкий математик Гаусс (1777 — 1855) доказал основную теорему алгебры: любое алгебраическое уравнение 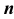-й степени имеет ровно 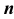комплексных корней, если каждый корень считать столько раз, какова его кратность.
Примеры:
Решить уравнения: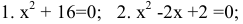 
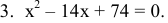
Решение:
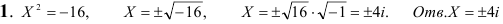
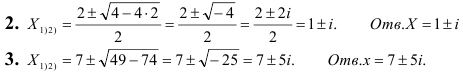
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Комплексные числа |
| Действия с комплексными числами в алгебраической форме |
| Тригонометрическая форма комплексных чисел |
| Действия с комплексными числами, заданными в тригонометрической форме |
