Оглавление:
Рациональной дробью называют частное двух многочленов одного и того же аргумента
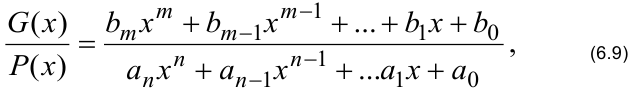
где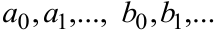 
— действительные числа.
Рациональная дробь (6.9) называется правильной, если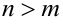 
. При 
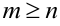дробь называется неправильной, в этом случае делением числителя на знаменатель можно выделить целую часть, которая будет многочленом степени 
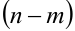и дробный остаток, который является правильной дробью. Такую процедуру называют выделением целой части.
Пример №1
В неправильной рациональной дроби выделить целую часть и правильный рациональный остаток:
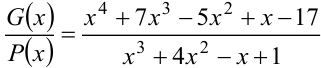
Решение:
Разделим числитель на знаменатель «уголком».
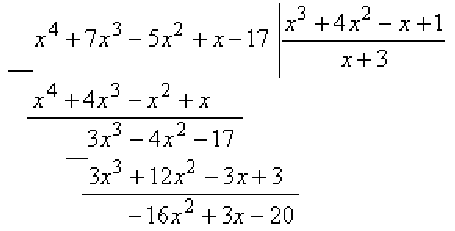
В результате получим: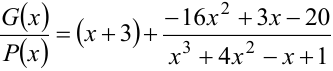 
.
Пусть дробь (6.9) — правильная. Предположим, что её знаменатель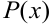 
можно разложить на множители
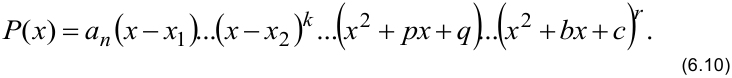
Здесь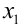 
— простой корень многочлена , 
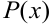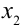— корень кратности 
.
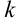Квадратные трёхчлены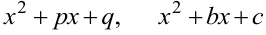 
не имеют действительных корней. Тогда правильную дробь (6.9) можно представить суммой простейших дробей.
Зависимость типа простейшей дроби от характера корней знаменателя
- Каждому простому действительному корню соответствует простейшая дробь 1-го типа.
- Каждому кратному действительному корню кратности 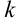соответствует одна дробь 1-го типа и
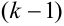дробей 2-го типа, показатель степени знаменателя которых возрастает от 2-й до 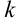-й. - Каждому простому многочлену второй степени с отрицательным дискриминантом соответствует простейшая дробь 3-го типа.
- Каждому кратному многочлену второй степени с отрицательным дискриминантом соответствуют простейшие дроби 3-го и 4-го типа.
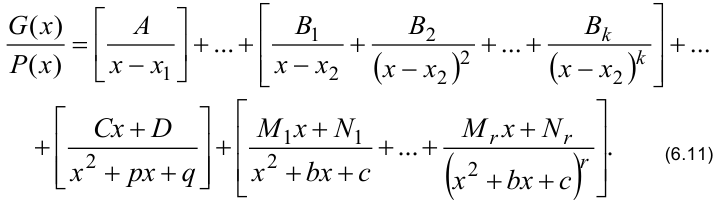
Выражения в каждой квадратной скобке соответствуют каждому множителю в разложении (6.10).
Неизвестные коэффициенты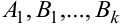 
, 
, 
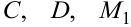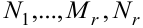определяются путём приведения правой части (6.11) к общему знаменателю.
Затем используют равенство числителей полученной и исходной дроби, приравнивая коэффициенты при одинаковых степенях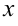 
.
Другой прием заключается в том, что переменной 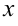в равенстве числителей задают ряд числовых значений, причем «удобными» значениями являются действительные корни знаменателя.
И в том и в другом случае образуется система алгебраических уравнений относительно неизвестных коэффициентов.
Пример №2
Разложить на простейшие дроби
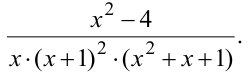
Решение:
Простому корню знаменателя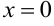 
соответствует одна простейшая дробь, корню 
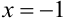кратности 2 соответствуют две простейшие дроби. Квадратный трёхчлен 
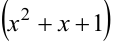не имеет действительных корней, ему соответствует одна простейшая дробь, в числителе которой — линейный двучлен.
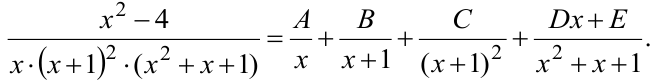
Приводим правую часть к общему знаменателю, приравнивая затем числители левой и правой частей. Получим тождество:
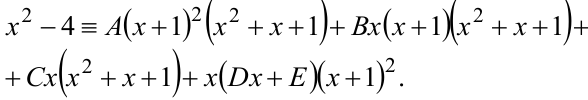
Подставляя в тождество различные значения 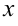, получаем уравнения относительно неизвестных коэффициентов (в первую очередь используем значения 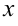, равные корням знаменателя 0 и -1).
Пусть 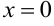, тогда 
.
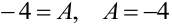Пусть 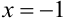, тогда 
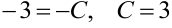. Задавая далее 
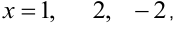получаем систему уравнений:
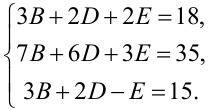
Решаем систему одним из методов (Крамера, Гаусса или матричным). Получим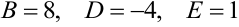 
. Запишем окончательный вид разложения заданной дроби на простейшие:
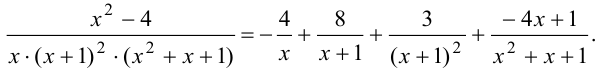
Вывод:
Определение интеграла от рациональной дроби производят в следующей последовательности.
- Выясняют, правильная дробь, или неправильная. Если дробь правильная, переходят к пункту 2. Если дробь неправильная, то выделяют целую часть и правильную рациональную дробь.
- Знаменатель правильной рациональной дроби разлагают на простейшие множители.
- Правильную рациональную дробь представляют суммой простейших дробей 1-4 типов и определяют неизвестные коэффициенты.
- Интеграл от исходной дроби равен сумме интегралов от целой части и простейших дробей.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Интегрирование простейших рациональных дробей |
| Разложение многочлена на множители |
| Интегралы от иррациональных функций |
| Интегрирование тригонометрических функций |
