Пример №14.
Рассмотрим такую систему уравнений
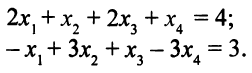
Переменная 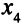 входит в первое уравнение с коэффициентом 1. Исключим ее из второго уравнения. Для этого прибавим ко второму уравнению первое, умноженное на 3. Система (3.10) станет такой
входит в первое уравнение с коэффициентом 1. Исключим ее из второго уравнения. Для этого прибавим ко второму уравнению первое, умноженное на 3. Система (3.10) станет такой
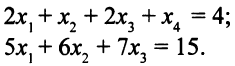
Выберем, например, переменную 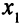 в качестве базисной для второго уравнения. Для этого сначала поделим на 5 все коэффициенты и правую часть второго уравнения, чтобы коэффициент при
в качестве базисной для второго уравнения. Для этого сначала поделим на 5 все коэффициенты и правую часть второго уравнения, чтобы коэффициент при 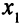 стал равным 1. Система (3.11) примет вид
стал равным 1. Система (3.11) примет вид
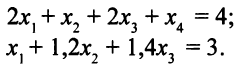
Исключим 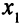 из первого уравнения. Для этого прибавим к первому уравнению второе, умноженное на -2. Получим систему
из первого уравнения. Для этого прибавим к первому уравнению второе, умноженное на -2. Получим систему
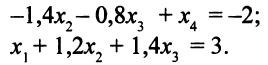
Система (3.13) — это та же исходная система (3.10), но решения системы (3.13) можно выписать сразу. Переменная 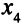 входит только в первое уравнение, ее можно выразить через переменные
входит только в первое уравнение, ее можно выразить через переменные 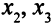 . По этой же причине переменная
. По этой же причине переменная 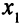 немедленно выражается через переменные
немедленно выражается через переменные 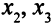 .
.
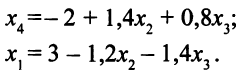
Переменные, не являющиеся базисными, называются свободными переменными. В нашем случае свободны переменные 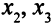 .
.
Если в совместной системе уравнений число неизвестных больше числа уравнений, то такая система имеет бесконечно много решений. Свободные переменные могут принимать любые значения, базисные переменные однозначно определяются через свободные. Например, если положить
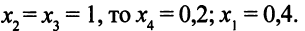
Систему уравнений, приведенную к виду, когда в каждом уравнении есть своя базисная переменная, назовем записанной в стандартной форме. Чтобы избежать громоздких обозначений, будем считать, что базисная переменная первого уравнения — это переменная 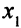 , второго —
, второго —  -го уравнения —
-го уравнения — 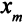 . Коэффициент в
. Коэффициент в 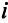 -м уравнении при переменной
-м уравнении при переменной 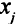 будем обозначать
будем обозначать 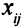 , правую часть
, правую часть 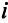 -го уравнения стандартной системы обозначим через
-го уравнения стандартной системы обозначим через 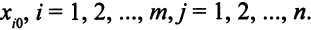 . Свободные переменные стандартной системы — это переменные
. Свободные переменные стандартной системы — это переменные 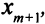
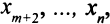 , они могут принимать любые значения. Значения базисных переменных однозначно вычисляются по значениям свободных. Система (3.9), приведенная к стандартной форме, такова
, они могут принимать любые значения. Значения базисных переменных однозначно вычисляются по значениям свободных. Система (3.9), приведенная к стандартной форме, такова
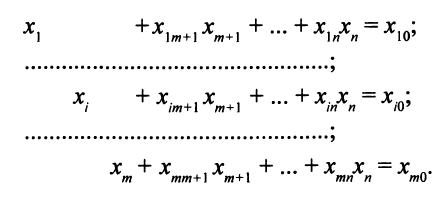
Общее решение системы (3.15) таково
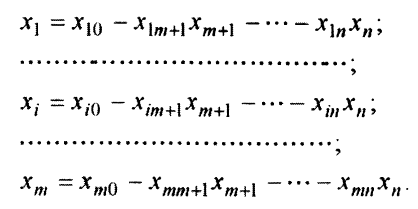
Эта задача взята со страницы решения задач по предмету «линейное программирование»:
Решение задач по линейному программированию
Возможно эти страницы вам будут полезны:
| Пример №12. Фирма производит два вида продукции |
| Пример №13. Привести к каноническому виду следующую ЗЛП |
| Пример №15. Общий способ избавления от вырожденности |
| Пример №16. Решить ЗЛП |

