Оглавление:
Производная от функции, заданной неявно
Теорема 17.1. Пусть непрерывная функция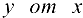 
задается уравнением
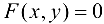
и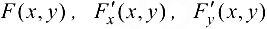 
— непрерывные функции в некоторой области D, содержащей точку 
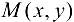, координаты которой удовлетворяют уравнению (17.1), причем 
.
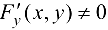Тогда функция будет иметь производную
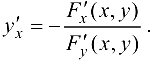
Доказательство.
Пусть некоторому значению 
соответствует значение функции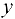 
, при этом 
.
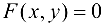Придадим независимой переменной 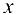приращение 
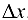, тогда функция 
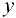получит приращение 
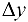, т. е. значению переменной 
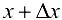соответствует значение функции 
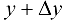. В силу (17.1)
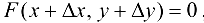
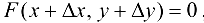, поэтому 
.
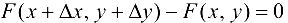Выражение слева представляет собой полное приращение функции двух переменных, которое также можно записать в виде:
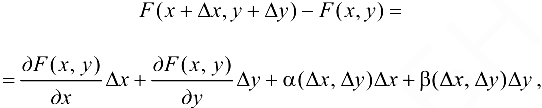
где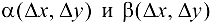 
— БМФ при 
.
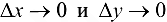Откуда
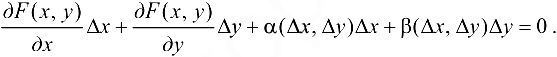
Разделим обе части равенства на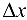 
и выразим 
:
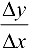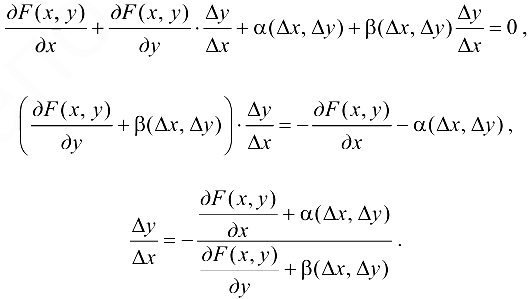
Переходя к пределу при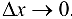 
, получим 
■
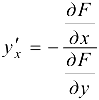Следует заметить, что в данном случае производная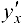 
, определяемая формулой (17.2), представляет собой производную 
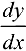функции одной переменной 
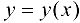, заданной неявно.
Пример 17.1.
Найти производную функции у, заданной уравнением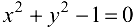 
.
Решение:
Заметим, что уравнение 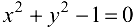задает две непрерывные функции 
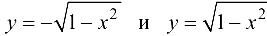, поэтому непосредственное вычисление производной не может быть выполнено.
Воспользуемся формулой (17.2). Так как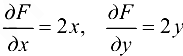 
то
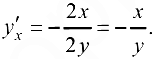
Ответ: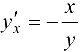 
.
Теорема 17.2*. Пусть функция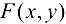 
непрерывна в окрестности точки 
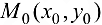и имеет в ней непрерывные частные производные, причем 
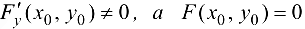. Toгда существует окрестность. содержащая точку 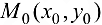, в которой уравнение 
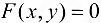определяет однозначную функцию 
.
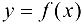Пусть функция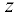 
от переменных 
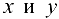задается уравнением
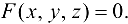
Найдем частные производные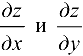 
. С читая переменную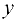 
постоянной и используя формулу (17.2), получим частную производную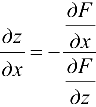 
. Аналогично можно получить 
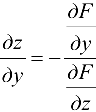. Заметим, что при получении формул использовано предположение 
.
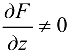Пример 17.2.
Найти частные производные функции 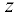, заданной уравнением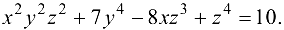 
Решение:
Преобразуем исходное уравнение к виду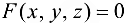 
и найдем частные производные 
.
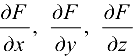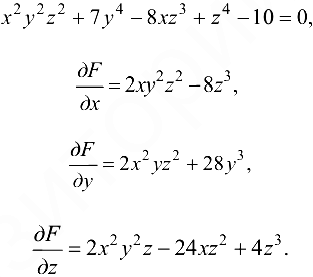
Воспользуемся формулами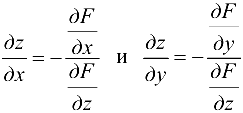 
Получаем
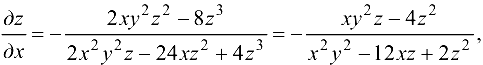
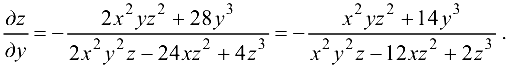
Ответ: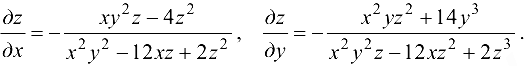 
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
