Производная фнп по направлению
Рассмотрим в области D непрерывную функцию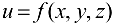 
, имеющую непрерывные частные производные по всем своим переменным. Проведем из некоторой точки 
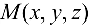данной области вектор 
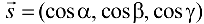. По направлению вектора 
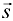на расстоянии 
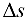от его начала, рассмотрим точку 
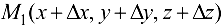, рис. 18.1
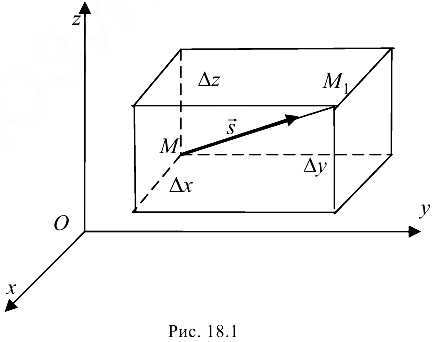
Таким образом,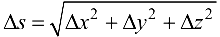 
.
Рассмотрим полное приращение функции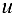 
:
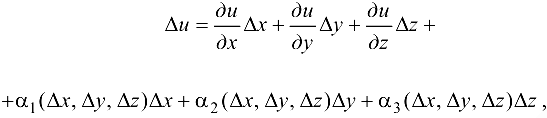
где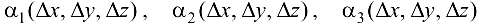 
— БМФ при 
Разделим обе части равенства (18.1) на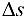 
:
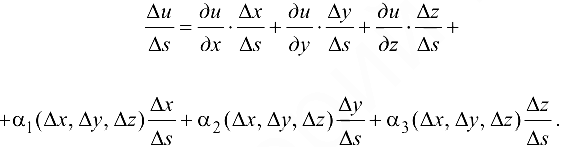
Очевидно,что
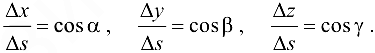
Следовательно, равенство (18.2) можно переписать в виде:
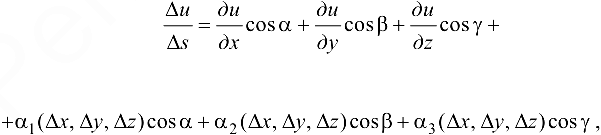
где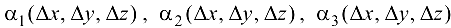 
— бесконечно малые функции при 
.
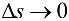Определение 18.1. Производной от функции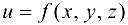 
в точке 
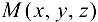по направлению вектора 
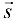называется предел отношения 
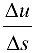при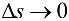
Обозначение: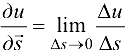 
.
Производная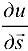 
показывает скорость изменения функции 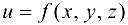в направлении вектора .
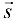Переходя к пределу в равенстве (18.3), получим
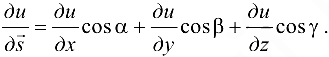
Из (18.4) следует, что, зная частные производные функции, легко найти производную по любому направлению вектора .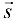
Заметим, что частные производные являются, по сути, частными случаями производной по направлению.
Так, например, при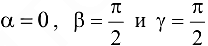 
:
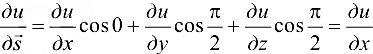
Пример 18.1. Для функции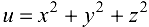 
найти производную 
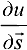в точке 
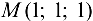по направлению вектора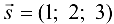 
Решение:
Найдем частные производные функции в точке Л/(1; 1; 1):
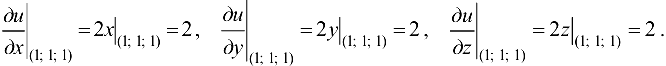
Так как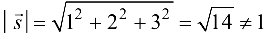 
, то направляющие косинусы вектора 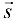будут определяться формулами: 
, 
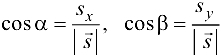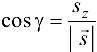. Тогда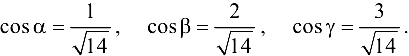 
Следовательно,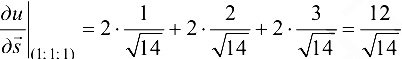 
.
Ответ: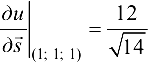 
.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
| Частные производные сложной функции с примерами решения |
| Производная от функции, заданной неявно с примерами решения |
| Определение градиента с примерами решения |
| Свойства градиента с примером решения |
