Оглавление:
Заметим, что признак Даламбера целесообразно применять в том случае, когда общий член ряда содержит выражение вида 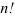 или
или 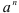 .
.
Иногда для исследования сходимости положительного ряда удобно использовать радикальный признак Коши, во многом схожий с признаком Даламбера.
Признак Коши (радикальный): Пусть дан положительный числовой ряд 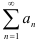 , и существует конечный или бесконечный предел
, и существует конечный или бесконечный предел 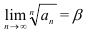 . Тогда:
. Тогда:
• если 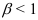 , то ряд
, то ряд 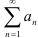 сходится;
сходится;
• если 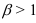 , то ряд
, то ряд 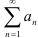 расходится;
расходится;
• если 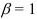 , признак не применяется (вопрос о сходимости ряда остается открытым).
, признак не применяется (вопрос о сходимости ряда остается открытым).
Исследовать ряд 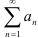 на сходимость но признаку Коши удобно по следующему неопределенности алгоритму:
на сходимость но признаку Коши удобно по следующему неопределенности алгоритму:
1)найти 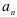 ;
;
2) найти 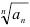 ;
;
3) найти 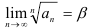 и проанализировать полученное значение:
и проанализировать полученное значение:
• если 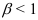 , то ряд
, то ряд 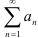 сходится;
сходится;
• если 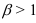 , то ряд
, то ряд 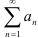 расходится;
расходится;
если 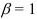 , то признак Коши ответа не дает (требуется дополнительное исследование).
, то признак Коши ответа не дает (требуется дополнительное исследование).
Пример решения заказа контрольной работы №97.
Исследуйте ряд 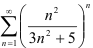 на сходимость, применяя признак Коши.
на сходимость, применяя признак Коши.
Решение:
Для исследования сходимости ряда но признаку Коши воспользуемся алгоритмом:
1) найдем
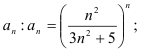
2) найдём
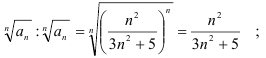
3) найдём
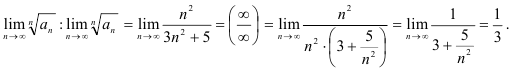
Получили, что 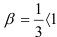 . Значит, но признаку Коши ряд
. Значит, но признаку Коши ряд 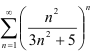 сходится.
сходится.
Ответ: 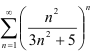 сходится.
сходится.
Заметим, что признак Коши целесообразно применять в том случае, когда общий член ряда представляет собой 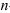 -ую степень выражения.
-ую степень выражения.
В некоторых ситуациях, когда ни один из признаков сравнения, Даламбера, Коши не дает ответ о сходимости положительного ряда, исследовать ряд на сходимость позволяет интегральный признак Коши.
Интегральный признак Коши: Если члены положительного ряда 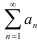 могут быть представлены как числовые значения некоторой непрерывной монотонно убывающей на промежутке
могут быть представлены как числовые значения некоторой непрерывной монотонно убывающей на промежутке 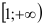 функции
функции 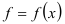 так, что
так, что 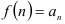 то данный ряд
то данный ряд 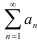 и несобственный интеграл
и несобственный интеграл 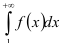 одновременно сходятся или расходятся.
одновременно сходятся или расходятся.
Пример решения заказа контрольной работы №98.
Исследуйте ряд 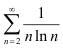 на сходимость, применяя интегральный признак Коши.
на сходимость, применяя интегральный признак Коши.
Решение:
Рассмотрим функцию 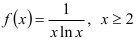 . Эта функция непрерывна, монотонно убывает на
. Эта функция непрерывна, монотонно убывает на 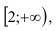 , и
, и 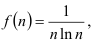 следовательно, можно применить интегральный признак Коши.
следовательно, можно применить интегральный признак Коши.
Выясним, будет ли несобственный интеграл 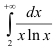 сходиться или расходиться.
сходиться или расходиться.
Имеем:
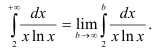
Отдельно найдём неопределённый интеграл 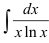 методом замены переменной:
методом замены переменной:
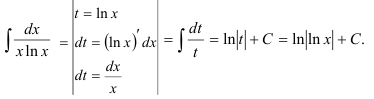
Найдем предел:
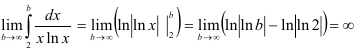
Таким образом, получили 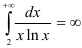 . Следовательно, несобственный интеграл
. Следовательно, несобственный интеграл 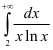 расходится. Значит, в силу интегрального признака Коши, ряд
расходится. Значит, в силу интегрального признака Коши, ряд 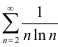 также будет расходиться.
также будет расходиться.
Ответ: 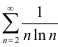 расходится.
расходится.
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:
Заказать контрольную работу по высшей математике
Другие похожие примеры возможно вам будут полезны:

