Оглавление:
Применение дифференциала в приближенных вычислениях
Рассмотрим формулу (6.2):
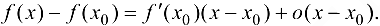
Откуда
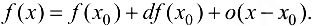
Если пренебречь 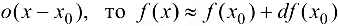 , или
, или
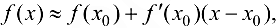
а это означает, что в достаточно малой окрестности точки х0 график функции 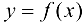 можно «заменить» графиком касательной
можно «заменить» графиком касательной
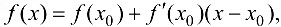
проведенной к графику функции в этой точке.
Если 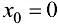 , то формула (6.3) принимает вид
, то формула (6.3) принимает вид 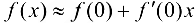 , и тогда очевидными становятся ряд эквивалентностей бесконечно малых функций.
, и тогда очевидными становятся ряд эквивалентностей бесконечно малых функций.
Пример 6.1.
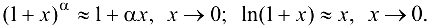
Основной принцип применения дифференциала к приближенным вычислениям значений функции сводится к следующему: если необходимо вычислить значение функции 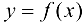 для
для 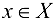 , но сделать это весьма затруднительно, то «вблизи» точки
, но сделать это весьма затруднительно, то «вблизи» точки 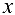 выбирается точка
выбирается точка 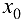 , такая, чтобы значения
, такая, чтобы значения 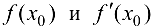 находились легко, и на основании (6.3) приближенно вычисляется значение
находились легко, и на основании (6.3) приближенно вычисляется значение 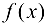 .
.
Пример 6.2.
Вычислить приближенно 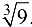 .
.
Решение:
Рассмотрим функцию 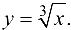 . Пусть
. Пусть 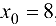 , тогда
, тогда 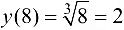 ,
, 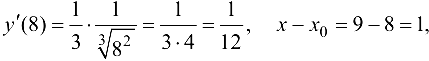 и на основании формулы (6.3) получим
и на основании формулы (6.3) получим 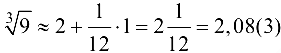 .
.
Ответ: 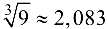 .
.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:

