Гидравлика

Гидра́влика (др.-греч. ὑδραυλικός — водяной; от др.-греч. ὕδωρ — вода + др.-греч. αὐλός — трубка) — прикладная наука о законах движения (см. гидродинамика капельных жидкостей и газов), равновесии жидкостей (см. гидростатика) и способах приложения этих законов к решению задач инженерной практики.

В отличие от гидромеханики, гидравлика характеризуется особым подходом к изучению явлений течения жидкостей: она устанавливает приближённые зависимости, ограничиваясь во многих случаях рассмотрением одноразмерного движения, широко используя при этом эксперимент, как в лабораторных, так и в натурных условиях.

Наряду с этим намечается всё большее сближение между гидромеханикой и гидравликой: с одной стороны, гидромеханика всё чаще обращается к эксперименту, с другой — методы гидравлического анализа становятся более строгими. wikipedia.org/wiki/Гидравлика

Введение в гидравлику

Гидравлика, как раздел физики, изучает законы равновесия и движения материальных тел различных видов. Она разделяется на:

• механику твёрдого тела, которая изучает покой и движение тел как совокупности сильно связанных материальных точек;
• механику сыпучих сред, изучающую движение песчаных грунтов, зерна и других аналогичных тел;
• механику жидких сред, в которой изучают равновесие и движение жидкости.

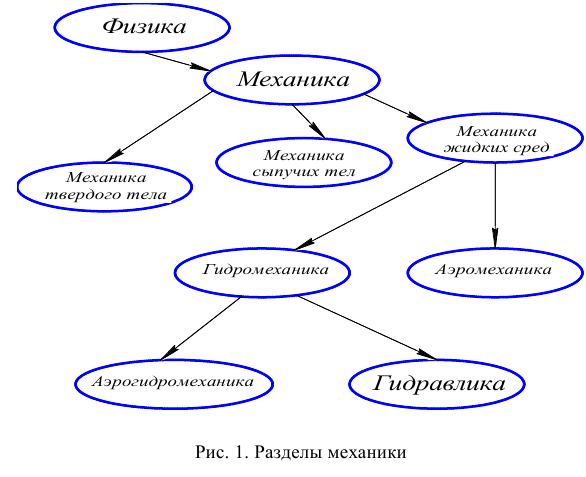
Часть механики жидких сред, которая рассматривает движение жидкости, а также силовое взаимодействие между жидкостью и обтекаемыми ею телами или ограничивающими ее поверхностями, называется гидромеханикой (рис. 1).

Раздел гидравлики, в котором изучают движение газов и жидкостей и обтекание ими тел, называют аэромеханикой.

Прикладную часть гидравлики, для которой характерен определенный круг технических вопросов, задач и методов их решения, называют технической механикой жидкости или гидравликой. Название «гидравлика» происходит от греческого «hydravlikos», что означает водяной.

Обычно гидравлику определяют как науку о законах равновесия и движения жидкостей и о способах приложения этих законов к решению практических задач. В гидравлике рассматриваются главным образом потоки жидкости, ограниченные и направленные твердыми стенками, то есть течения в открытых и закрытых руслах (каналах). Можно сказать, таким образом, что в гидравлике изучают внутренние течения жидкостей и решают гак называемую «внутреннюю» задачу в отличие от «внешней» задачи, связанной с внешним обтеканием тел сплошной средой, которое имеет место при движении твердого тела в жидкости или газе (воздухе). «Внешнюю» задачу рассматривают в собственно гидромеханике или аэрогидромеханике. Этот раздел в основном связан с потребностями авиации и судостроения.

Подавляющее большинство технологических процессов практически в любой отрасли современного производства в той или иной степени связаны с использованием жидкостей, газов или паров. Особенно это касается таких отраслей промышленности, как химическая и нефтехимическая отрасли, включая добычу, транспортировку и переработку нефти и газа. И во многом, благодаря накопленным знаниям о закономерностях поведения жидкостей и газов, в условиях современных производств удается не только успешно повышать эффективность существующих технологий, но и разрабатывать новые и весьма перспективные технологии. Это касается всех без исключения технологических процессов, которые протекают в динамических условиях, т.е. в таких условиях, которые не только непосредственно, но и, прежде всего, связаны с движением жидкостей и газов. Это такие технологические процессы, как гидромеханические, теплообменные и массообменные процессы, а также процессы, связанные с химическими превращениями.

При протекании указанных процессов в условиях движения в объеме жидкостей и газов зависимости от физико-химических свойств и внешних сил вначале формируются поля скоростей, затем температурные и поля концентраций. Эти поля в конечном итоге определяют величину движущих сил и направления протекания процессов. По этой причине при изучении любого технологического процесса особое значение приобретают вопросы, связанные изучением закономерностей течения жидкостей и газов, что является основным предметом изучения гидравлики.

В гидравлике при решении различных практических задач широко используются те или иные допущения и предположения, упрощающие рассматриваемый вопрос. Достаточно часто гидравлические решения основываются на результатах экспериментов, и потому в гидравлике применяется относительно много различных эмпирических и полуэмпирических формул. При этом, как правило, оцениваются только главные характеристики изучаемого явления и часто используются те или иные интегральные и осредненные величины, которые дают достаточную для технических задач характеристику рассматриваемых явлений.

По своему характеру техническая механика (гидравлика) близка к известным дисциплинам — сопротивлению материалов и строительной механике, в которых под тем же углом зрения изучаются вопросы механики твердого тела. Следует учитывать, что гидравлика, являясь общетехнической дисциплиной, может рассматриваться как «профессиональная физика жидкого тела», в которой, в частности, даются основы соответствующих гидравлических расчетов. Эти расчёты используются при проектировании инженерных гидротехнических сооружений, конструкций, а также гидросистем технологического оборудования, применяемых во многих областях техники.

Разумеется, что гидравлика разделяется на статику жидкости (гидростатику), кинематику потоков жидкости и динамику жидкости (гидродинамику).

Метод, применяемый в современной гидравлике при исследовании движения, заключается в следующем. Исследуемые явления сначала упрощают, и к ним применяют законы теоретической механики. Затем полученные результаты сравнивают с данными опытов, выясняют степень расхождения, уточняют и исправляют теоретические выводы и формулы для приспособления их к практическому использованию. Целый ряд явлений, крайне трудно поддающихся теоретическому анализу, ввиду своей сложности, исследуют экспериментальным путем, а результаты такого исследования представляют в виде эмпирических формул.

Особенно велико значение гидравлики в машиностроении, где приходится иметь дело с закрытыми потоками в трубах и давлениями, многократно превышающими атмосферное. Гидросистемы, состоящие из насосов, трубопроводов, различных гидроагрегатов, широко используют в машиностроении в качестве устройств передачи и преобразования энергии, жидкостного охлаждения, топливоподачи, смазки и др.

Можно также отметить, что имеет место и другой подход к классификации разделов механики жидких сред. В этом подходе говорят о двух разных методах исследования:

• метод «технической механики жидкости» («технической гидромеханики », «гидравлики »),
• метод «математической механики жидкости» («математической гидромеханики »).

В математической механике жидкости широко используется относительно сложный математический аппарат. Решения, получаемые в этом случае, оказываются более строгими в математическом отношении.

Как показал опыт, методы математической механики жидкости очень часто оказываются столь сложными, что громадное большинство практических задач, следуя этим методам, решить невозможно. Этим и объясняется возникновение и развитие технической, прикладной науки — технической механики жидкости, т. е. гидравлики, которая стремится дать приближенные ответы на все те вопросы, связанные с движущейся или покоящейся жидкостью, которые ставит перед нами практика.

Можно сказать, что в технической гидромеханике (в гидравлике) приближенно решаются сложные задачи при помощи простых методов. В математической же гидромеханике относительно точно решаются только некоторые простейшие задачи при помощи сложных методов.

История развития гидравлики

Зарождение отдельных представлений из области гидравлики следует отнести еще к глубокой древности, ко времени гидротехнических работ, проводившихся древними народами, населявшими Египет, Вавилон, Месопотамию, Индию, Китай и другие страны. Однако прошло много веков и даже тысячелетий, прежде чем начали появляться отдельные, вначале не связанные друг с другом, попытки выполнить научные обобщения тех или других наблюдений, относящихся к гидравлическим явлениям. В далекой древности гидравлика являлась только ремеслом без каких-либо научных основ.

Период Древней Греции. В Греции еще за 250 лет до н.э. начали появляться трактаты, в которых уже выполнялись достаточно серьезные для того времени теоретические обобщения отдельных вопросов механики жидкости. Математик и механик того времени Архимед (около 287 — 212 гг. до н.э.) выполнил анализ вопросов по гидростатике и плаванию тел. За истекшее время к труду Архимеда, посвященному гидростатике, мало что удалось добавить. Представитель древнегреческой школы Ктесибий (II или I век до н.э.) изобрел пожарный насос, водяные часы и некоторые другие гидравлические устройства. Герону Александрийскому (вероятно, I век н.э.) принадлежит описание сифона, водяного органа, автомата для отпуска жидкости ит. п.

Период Древнего Рима. Римляне заимствовали многое у греков. В Древнем Риме строились сложные для того времени гидротехнические сооружения: акведуки, системы водоснабжения и т. п. В своих сочинениях римский инженер-строитель Фронтин (40 — 103 г. н.э.) указывает, что во времена Траяна в Риме было 9 водопроводов, причем общая длина водопроводных линий составляла 436 км. Можно предполагать, что римляне уже обращали внимание на наличие связи между площадью живого сечения и уклоном дна русла, на сопротивление движению воды в трубах, на неразрывность движения жидкости. Например, Секст Юлий Фронтин писал, что количество воды, поступившей в трубу, должно равняться количеству воды, вытекающей из нее.

Период Средних веков. Этот период, длившийся около тысячи лег после падения Римской империи, характеризуется регрессом, в частности и в области механики жидкости.

Эпоха Возрождения. В течение второй половины XV века и в XVI веке начали развиваться экспериментальные исследования, постепенно опровергавшие схоластические воззрения, поддерживаемые католической церковью. В этот период в Италии появилась гениальная личность — Леонардо да Винчи (1452 — 1519), который, как известно, вел свои научные (экспериментальные и теоретические) исследования в самых различных областях. В частности, Леонардо изучал принцип работы гидравлического пресса, аэродинамику летательных аппаратов, образование водоворотных областей, отражение и интерференцию волн, истечение жидкости через отверстия и водосливы. Он изобрел центробежный насос, парашют, анемометр. Различные работы Леонардо отражены в сохранившихся 7 тыс. страниц его рукописей, хранящихся в библиотеках Лондона, Виндзора, Парижа, Милана и Турина. По-видимому, справедливо будет признать, что Леонардо да Винчи является основоположником механики жидкости.

К периоду Возрождения относятся работы нидерландского математика и инженера Симона Стевина (1548 — 1620), определившего величину гидростатического давления на плоскую фигуру и объяснившего «гидростатический парадокс». В этот период великий итальянский физик, механик и астроном Галилео Галилей (1564 — 1642) показал, что гидравлические сопротивления возрастают с увеличением скорости и с возрастанием плотности жидкой среды; он разъяснял также вопрос о вакууме.

Период XVII века и начало XVIII века. В это время механика жидкости все еще находилась в зачаточном состоянии. Вместе с тем здесь можно отметить имена следующих ученых, способствовавших ее развитию. Бенедетто Кастелли (1577 — 1644) — преподаватель математики в Пизе и Риме, в ясной форме изложивший принцип неразрывности. Эванджелиста Торричелли (1608 — 1647) — выдающийся математик и физик — вывел формулу расчета скорости истечения жидкости из отверстия и изобрел ртутный барометр. Блез Паскаль (1623 1662) — выдающийся французский математик и физик, установивший, что значение гидростатического давления не зависит от ориентировки площадки действия, кроме того, он окончательно решил и обосновал вопрос о том, что такое вакуум. Исаак Ньютон (1643 — 1727) -гениальный английский физик, механик, астроном и математик, давший наряду с решением ряда вопросов гидравлики приближенное описание законов внутреннего трения жидкости.

Середина и конец XVIII века. Формируются теоретические основы современной механики жидкости. Анализируя соответствующий исторический материал, можно видеть, что вопрос о вакууме осознавался человечеством на протяжении 2 тыс. лет (от Аристотеля, неправильно осветившего этот вопрос, до Паскаля); вопрос о неразрывности движения жидкости — на протяжении 1,5 тыс. лет (от Фронтина до Кастелли). Такое положение объясняется тем, что прежде чем уяснить подобные вопросы (с современной точки зрения достаточно простые), следовало предварительно ясно себе представить основные положения физики и механики, которые в наше время люди усваивают с детского возраста: вопрос о природе силы тяжести и всемирном тяготении, вопрос о скорости и ускорении, о давлении атмосферы и т. п. Только освоив такие представления, можно легко разобраться в «элементарных» положениях механики жидкости. Однако решение всех этих вопросов физики и механики являлось весьма трудной задачей. На пути раскрытия их стояла католическая церковь, различные предрассудки, а также существовавшие метафизические объяснения различных явлений (например, говорили, что снаряд летит в воздухе потому, что тот, кто отлил его, ввел в него известную силу, которая и обусловливает движение снаряда; Аристотель учил, что летящую стрелу приводит в движение воздух и т. п.).

И вот к середине XVIII века трудами ряда ученых (Галилея, Коперника, Кеплера, Паскаля, Декарта, Гука, Ньютона, Лейбница, Ломоносова, Клеро и многих других) указанные препятствия, наконец-то, были в значительной мере преодолены. После этого относительно быстро начали создаваться современные научные основы механики жидкости. Эти научные основы были заложены тремя учеными XVIII века: Даниилом Бернулли, Леонардом Эйлером и Жаном Лероном Д’Аламбером.

Даниил Бернулли (1700 — 1782) — выдающийся физик и математик родился в Гронингене (Голландия). С 1725 но 1733 г. жил в Петербурге, являлся профессором и членом Петербургской Академии наук. В Петербурге он написал свой знаменитый труд «Гидродинамика», который был впоследствии опубликован (в 1738 г.) в Страсбурге. В этом груде он осветил ряд основополагающих вопросов гидравлики и в частности объяснил физический смысл слагаемых, входящих в современное уравнение установившегося движения (идеальной жидкости), носящее его имя.

Леонард Эйлер (1707 — 1783) — великий математик, механик и физик родился в Базеле (Швейцария). Жил в Петербурге с 1727 до 1741 г. и с 1766 г. до конца жизни. Был членом Петербургской Академии наук. Умер в Петербурге. Могила его находится в Ленинградском некрополе. Эйлер не только подытожил и обобщил в безупречной математической форме работы предшествующих авторов, но составил известные дифференциальные уравнения движения и относительного равновесия жидкости, носящие его имя, а также опубликовал целый ряд оригинальных решений гидравлических задач, широко используя созданный к тому времени математический аппарат.

Жано Лерон Д’Аламбер (1717 — 1783) — математик и философ; член Парижской, Французской и других Академий наук, а также Петербургской Академии наук (с 1764 г.). Опубликовал ряд трактатов, относящихся к равновесию и движению жидкости; предполагают, что Д’Аламбер первый отметил возможность возникновения кавитации в жидкости.

В указанный период существенный вклад в дело развития механики жидкости внесли также два выдающихся французских математика того времени: Жозеф Луи Лагранж (1736 — 1813), который ввел понятие потенциала скорости и исследовал волны малой высоты, и Пьер-Симон Лаплас (1749 — 1827), создавший, в частности, особую теорию волн на поверхности жидкости.

Середина и конец XVIII века. Зарождается техническое (прикладное) направление механики жидкости. Наряду с учеными Эйлером, Бернулли, Д’Аламбером и др., сформулировавшими основы современной механики жидкости, в середине и в конце XVIII в. во Франции начала постепенно образовываться особая школа — школа ученых-инженеров, которые стали формировать механику, как прикладную (техническую) науку. Рассматривая гидравлику, как отрасль техники, а не математики, представители этой школы ввели преподавание механики жидкости в технических учебных заведениях. К концу XVIII в. французская школа стала основной гидравлической школой в области технических наук.

Яркими представителями этой школы явились: Анри Пито (1695 1771) — инженер-гидротехник, член Парижской Академии наук, изобретатель «трубки Пито»; Антуан Шези (1718 — 1798) — директор Французской школы мостов и дорог, сформулировавший параметры подобия потоков и обосновавший формулу, носящую его имя; Жан Борда (1733 — 1799) — военный инженер, который занимался вопросами истечения жидкостей из отверстий и нашел зависимость для потерь напора при резком расширении потока; Пьер Дюбуа (1734 — 1809) инженер-гидротехник и военный инженер, составивший обобщающий труд «Принципы гидравлики».

Техническое направление механики жидкости развивалось и в других странах. Здесь можно отметить итальянского профессора Джованни Баггиста Вентури (1746 — 1822) и немецкого ученого-инженера Рейнхарда Вольгмана (1757 — 1837).

В результате деятельности ученых-инженеров техническая механика жидкости (гидравлика) обогатилась изобретением соответствующей измерительной аппаратуры (пьезометрами, трубками Пито, вертушками Вольтмана и т.п.); идеей использования материальных (вещественных) моделей тех или других гидравлических явлений для их изучения и для проектирования соответствующих инженерных сооружений; идеей теоретического построения приближенных расчетных зависимостей с уточнением таких зависимостей при помощи введения в них эмпирических коэффициентов.

Вне зависимости от формирования технической механики жидкости в странах Западной Европы гениальный русский ученый М. В. Ломоносов (171 1 — 1765), учитывая рост промышленности и строительства в России, начал также развивать механику жидкости в техническом направлении.

Развитие технической механики жидкости (гидравлики) в XIX в. за рубежом. Зародившееся во Франции техническое (гидравлическое) направление механики жидкости быстро начало развиваться как в самой Франции, гак и в других странах. В этот период в той или другой мере были разработаны или решены следующие проблемы: основы теории плавно изменяющегося неравномерного движения жидкости в открытых руслах (Беланже, Кориолис, Сен-Венан, Дюпюи, Буден, Бресс, Буссинеск); вопрос о гидравлическом прыжке (Бидоне, Беланже, Бресс, Буссинеск); экспериментальное определение параметров, входящих в формулу Шези (Базен, Маннинг, Гангилье, Куттер); составление эмпирических и иолуэмпирических формул для определения гидравлических сопротивлений в различных случаях (Кулон, Хаген, Сен-Венан, Пуазейль, Дарси, Вейсбах, Буссинеск); открытие двух режимов движения жидкости (Хаген, Рейнольде); получение гак называемых уравнений Навье-Стокса, а также уравнений Рейнольдса на основе использования модели осредненного турбулентного потока (Сен-Вснан, Рейнольде, Бусеинеек); установление принципов гидродинамического подобия, а также критериев подобия (Коши, Риич, Фруд, Гельмгольц, Рейнольде); основы учения о движении грунтовых вод (Дарси, Дюпюи, Буссинеск); теория волн (Герстнер, Сен-Венан, Риич, Фруд, Стоке, Гельмгольц, Базен, Буссинеск); вопросы истечения жидкости через водосливы и отверстия (Беланже, Кирхгоф, Базен, Буссинеск, Борда, Вейсбах). В этот период изучались также взвесенесущие потоки (Фарг, Дюпюи), неустановившееся движение (Сен-Венан, Буссинеск, Дюпюи).

Зарождение и развитие технической механики жидкости (гидравлики) в XIX в. в России. Прикладное, инженерное направление механики жидкости, зародившееся у нас еще в работах М.В. Ломоносова, стало развиваться в России в XIX в. в стенах Петербургского института инженеров путей сообщения. В этом институте долгое время существовала единственная гидравлическая школа России. Ученые этого института только в начале своей деятельности следовали французской гидравлической школе. Здесь можно прежде всего упомянуть П.П. Мельникова (1804 — 1880) инженера путей сообщения, профессора прикладной механики, почетного члена Петербургской Академии наук, министра путей сообщения, который создал первый на русском языке курс «Основания практической гидравлики…», а также организовал в 1855 г. первую в России учебную гидравлическую лабораторию. Преемниками П. П. Мельникова являлись профессора того же института B.C. Глухов, Н.М. Соколов, П.П. Когляревский, Ф.Е. Максименко и Г.К. Мерчинг. Они опубликовали ряд трудов, относящихся к технической механике жидкости (гидравлике), в которых обобщили соответствующие исследования, выполненные в стенах института инженеров путей сообщения.

Большой вклад внесли в развитие гидравлики следующие русские ученые и инженеры: Н.П. Петров (1836 — 1920) — выдающийся русский ученый-инженер, почетный член Петербургской Академии наук (инженер-генерал-лейтенант), который в своем труде «Трение в машинах и влияние на него смазывающей жидкости» (1883 г.) впервые сформулировал законы трения при наличии смазки: Н.Е. Жуковский (1847 — 1921) — великий русский ученый, профессор Московского высшего технического училища и Московского университета, член-корреспондент Петербургской Академии наук, создатель теории гидравлического удара, исследовавший также многие другие вопросы механики жидкости; И.С. Громека (1851 — 1889) — профессор Казанского университета, разрабатывавший теорию капиллярных явлений и заложивший основы теории винтовых потоков.

Развитие технической механики жидкости (гидравлики) в области инженерно-строительных специальностей в течение первых десятилетий XX века. В начале XX в. в гидравлике наметилось много самых различных научных направлений, которые можно классифицировать по разным признакам, например:

а) по виду рассматриваемой текучей среды; здесь можно различать воду, воздух, нефть, разные двухфазные жидкости, так называемые, неньютоновские и аномальные жидкости, электропроводящую или магнитную среду, плазму; сюда можно отнести стратифицированные потоки и т. п.;

б) в зависимости от отрасли техники или отрасли знаний, где используется аппарат гидромеханики, можно различать: аэронавтику, судостроение, гидромашиностроение, инженерно-строительное дело (в частности, гидротехнику), баллистику, гидроавтоматику, химическую технологию, метеорологию, океанологию и т. п.;

в) можно различать отдельные гидромеханические теории, которые иногда полагаются в основу решения задач, относящихся к различным областям техники: теорию турбулентности; задачи неустановившегося, в частности, волнового движения; теорию смазки и ламинарного движения; теорию движения жидкости (в частности, нефти и газа) в пористых средах и т.п.

В связи со сказанным в начале XX в. (да и в конце XIX в.) из технической механики жидкости начали выделяться отдельные, иногда в значительной мере изолированные друг от друга направления, которые приходится рассматривать отдельно. Ниже, касаясь только инженерно-строительного направления гидравлики, осветим главнейшие работы, относящиеся к этому направлению и выполненные в период до 20-30-х годов настоящего столетия. Фридрих Форхгеймер (1852 — 1933) — немецкий профессор — рассмотрел гидравлические сопротивления, волны перемещения, колебания горизонтов воды в уравнительных резервуарах ГЭС, некоторые виды деформаций песчаных русел. Особенно важны исследования Форхгеймера в области вопросов фильтрации. Макс Вебср (1871 — 1951) — немецкий профессор придал принципам гидродинамического подобия современные формы. Людвиг Прандтль (1875 — 1953) — немецкий профессор, инженер разработал (наряду с Тейлором и Карманом) полуэмпирическую теорию турбулентности; исследовал гидравлические сопротивления в трубах. С именем Прандтля связан ряд понятий из области механики жидкости. Работы Прандтля в области теории пограничного слоя явились основополагающими. М.А. Великанов (1879 — 1964) советский ученый, член-корреспондент АН СССР разрабатывал теорию турбулентности, исследовал движение наносов и русловые деформации, предложил так называемую гравитационную теорию движения взвешенных наносов. Б.А. Бахметев (1880 — 1951) — русский ученый, инженер путей сообщения, работая в Петербургском политехническом институте, заложил основы современной русской гидравлической школы, опубликовав ряд книг, в которых осветил различные разделы гидравлики. Б.А. Бахметев решил в достаточно общей форме задачу об интегрировании дифференциального уравнения неравномерного движения в призматических руслах. Рихард Блазиус (1883 — 1970) немецкий ученый — впервые показал, что для «гладких труб» коэффициент сопротивления зависит только от одного параметра -числа Рейнольдса. Н.Н. Павловский (1886 — 1937) — советский ученый, академик, инженер путей сообщения — в 1922 г. опубликовал основы математической теории фильтрации воды в грунтах; предложил метод электрогидродинамических аналогий (метод ЭГДА) фильтрационных потоков; издал первый в России «Гидравлический справочник» и монографию по основам гидравлики; решил ряд гидравлических задач, относящихся к инженерно-строительной гидравлике. Н.Н. Павловский создал научно-педагогическую школу в области гидравлики на базе общеинститутской кафедры гидравлики Ленинградского политехнического института. Н.М. Вернадский (1882 — 1935) -советский ученый, инженер путей сообщения — впервые связал определение тепловых потерь с полем скоростей в прудах-охладителях; предложил важную модель «планового потока», нашедшую себе широкое применение.

К 20-30-м годам XX в. была создана обширная лабораторная база, на основе которой решались самые различные вопросы гидравлики. Равным образом были проведены также обширные натурные (нолевые) наблюдения, позволившие составить соответствующие эмпирические формулы или откорректировать (применительно к реальным условиям) формулы, полученные для различных идеализированных схем теоретическим путем.

Общая схема формирования (во времени) механики жидкости, как видно из рис. 2, в соответствии со всем сказанным выше, можно считать с некоторым приближением, что наука о механике жидкости (в современном представлении этого понятия) зародилась в трудах Архимеда.

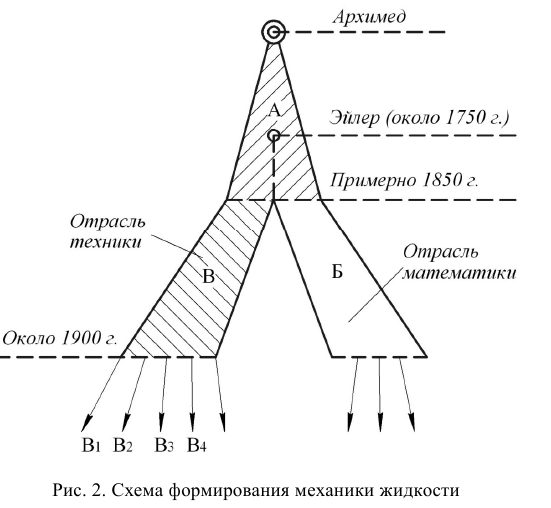
Примерно к середине XIX в. данная наука (область А, см. рис. 2) получила значительное развитие, причем в этот период времени произошло разделение механики жидкости на два различных направления: «математическую механику жидкости» (область Б, см. рис. 2) и «техническую механику жидкости» (область В, см. рис. 2). Как отмечают (например, Г. Рауз и С. Инце в своей известной книге «История гидравлики»), математическая механика жидкости зародилась еще в трудах Я. Эйлера (в середине XVIII в.). Что касается технической механики жидкости (гидравлики), то это направление механики, как выше было сказано, начало развиваться главным образом в работах французских ученых-инженеров. Важно подчеркнуть, что на рубеже начала XIX в. техническая механика жидкости начала в свою очередь расчленяться на отдельные направления (стрелки В и В2, Вз, см. рис. 2). К таким отдельным направлениям можно отнести, например, инженерно-строительную (гидротехническую) гидравлику,

гидромашинную гидравлику, судостроительную гидравлику, нефтяную и газовую гидравлику и т.п.

Разумеется, теоретические основы этих отдельных гидравлик являются в значительной мере общими; вместе с тем чисто прикладные части таких курсов оказываются существенно различными. Заметим, что вопрос о разделении механики (в частности, механики жидкости) на различные направления достаточно часто подчеркивается в литературе. Например, А.Н. Боголюбов пишет: «В результате современная механика разделилась на много направлений, которые сливаются, с одной стороны, с математической, а с другой — с различными направлениями техники (такое промежуточное положение между чистой абстракцией и конкретной практикой было характерно для механики со времен ее зарождения)».

Некоторые общие выводы, вытекающие из рассмотрения исторического материала:

1. Разработка проблем гидравлики (технической механики жидкости), в частности, инженерно-строительного направления, всегда, диктовалась необходимостью решения тех или других практических задач, выдвигаемых жизнью и связанных с развитием материальной базы нашего общества.
2. Отдельные казалось бы элементарные представления механики жидкости осваивались человечеством, как мы видели, иногда в течение весьма продолжительного времени (например, отмеченные выше вопросы о вакууме и уравнения неразрывности движения жидкости, которые решались в течение тысячелетий).
3. 3.Теоретические основы технической механики жидкости (гидравлики) начали интенсивно развиваться только в середине XVIII в., после того как рядом зарубежных и отечественных ученых были сформулированы основополагающие законы физики и общей механики, а также был разработан соответствующий математический аппарат, позволяющий достаточно точно и кратко выражать соответствующие зависимости механики.
4. По-видимому некоторые положения гидромеханики на протяжении столетий повторно открывались и разрабатывались по нескольку раз.
5. Иногда, в конечном счете, отдельным ученым история приписывает то, что они не предлагали и «забывает» о том, что они сделали. Например, Фруд не предлагал «числа Фруда» и никогда им не пользовался (широко известно, что «число Фруда» было предложено Риичем).
6. Многие уравнения и формулы, связанные в настоящее время с именами различных ученых, были даны этими учеными совсем не в том виде, в каком они фигурируют в современной литературе; примеров таких «именных зависимостей» можно привести целый ряд: формула Шези, формула Торричелли, Вейсбаха, Жуковского и т. д.

Жидкость как объект изучения гидравлики

В теории гидромеханики иод термином «жидкость» подразумеваются капельные и упругие жидкости (газы и пары) благодаря их общему физическому свойству — текучести. Поэтому, прежде всего, в гидравлике и гидромеханических процессах жидкости рассматриваются как текучие среды (вещества), способные самопроизвольно занимать и принимать форму всего объема сосуда, в котором они заключены.

Различают следующие виды жидкостей:

• идеальная жидкость — обладает абсолютной текучестью, абсолютно не сжимаема и в ней полностью отсутствуют силы сцепления между частицами;
• реальная жидкость — обладает всеми указанными выше свойствами. Главные и основные свойства жидкости — текучесть и вязкость;
• гомогенная жидкость — жидкость, состоящая из одного или нескольких компонентов, не имеющих границу раздела между собой (истинные растворы);
• гетерогенная жидкость — жидкость, состоящая из одного или нескольких компонентов, которые имеют границу раздела между собой — двух или трехфазные системы (суспензии, дымы, пыли, туманы и эмульсии).

Жидкости, как и все вещества, имеют молекулярное строение (рис. 3). Они занимают промежуточное положение между газами и твердыми телами. Это определяется величинами межмолекулярных сил и характером движений составляющих их молекул. В газах расстояния между молекулами больше, а силы межмолекулярного взаимодействия меньше, чем в жидкостях и твердых телах, поэтому газы отличаются от жидкостей и твердых тел большей сжимаемостью. По сравнению с газами жидкости и твердые тела малосжимаемы.

Молекулы жидкости находятся в непрерывном хаотическом тепловом движении, отличающемся от хаотического теплового движения газов и твердых тел. В жидкостях это движение осуществляется в виде колебаний (1013 колебаний в секунду) относительно мгновенных центров и скачкообразных переходов ог одного центра к другому. Тепловое движение молекул твердых тел состоит в колебаниях относительно стабильных центров. Тепловое движение молекул газа выглядит как непрерывное скачкообразное изменение положения.

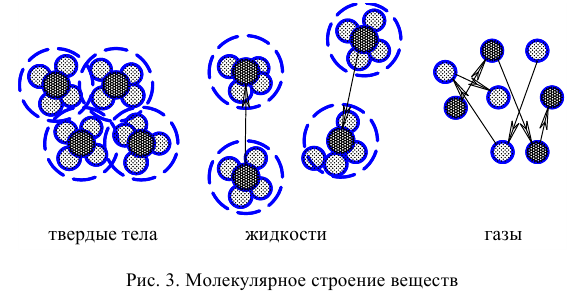
При этом надо заметить, что изменение температуры и давления приводят к изменениям свойств жидкостей. Установлено, что при повышении температуры и уменьшении давления свойства жидкостей приближаются к свойствам газов, а при понижении температуры и увеличении давления — к свойствам твердых тел.

Термин «жидкость» применяется для обозначения и собственно жидкости, которую рассматривают как несжимаемую или мало сжимаемую среду, и газа, который можно рассматривать как «сжимаемую жидкость».

Гипотеза сплошности

Рассматривать и математически описывать жидкость как совокупность огромного количества отдельных частиц, находящихся в постоянном непрогнозируемом движении, на современном уровне науки не представляется возможным. По этой причине жидкость рассматривается как некая сплошная деформируемая среда, имеющая возможность непрерывно заполнять пространство, в котором она заключена, среда, не имеющая ни пустот, ни разрывов. Другими словами, иод жидкостями понимают все тела, для которых характерно свойство текучести, основанное на явлении диффузии.

Текучестью можно назвать способность тела как угодно сильно менять свой объём под действием сколь угодно малых сил. Таким образом, в гидравлике жидкость понимают как абстрактную среду -континуум, который является основой гипотезы сплошности. Континуум считается непрерывной средой без пустот и разрывов, свойства которой одинаковы во всех направлениях. Это означает, что все характеристики жидкости являются непрерывными функциями и все частные производные по всем переменным также непрерывны.

По-другому такие тела (среды) называют капельными жидкостями. Капельные жидкости — это такие, которые в малых количествах стремятся принять шарообразную форму, а в больших образуют свободную поверхность.

Очень часто в математических описаниях гидравлических закономерностей используются понятия «частица жидкости» или «элементарный объём жидкости». К ним можно относиться как к бесконечно малому объёму, в котором находится достаточно много молекул жидкости. Например, если рассмотреть кубик воды со сторонами размером 0,001 см, то в объеме будет находиться 3,3-1013 молекул. Частица жидкости полагается достаточно малой по сравнению с размерами области, занятой движущейся или покоящейся жидкостью.

Сплошная среда представляет собой модель, которая успешно используется при исследовании закономерностей покоя и движения жидкости. Правомерность применения такой модели жидкости подтверждена всей практикой гидравлики.

Возникает естественный вопрос: при каких предположениях справедлива эта гипотеза? Если для жидкостей (воды, жидких металлов и т.п.) эта гипотеза более или менее очевидна, то для достаточно разреженных газов (например, занимающих космическое пространство, включая атмосферы звезд, планет и Солнца), которые состоят из отдельных атомов или молекул, а также других физических объектов, к которым применим аппарат гидроаэромеханики, она требует своего обоснования. Так, например, при расчете торможения искусственных спутников Земли использование математического аппарата гидроаэромеханики не представляется возможным, в то время как именно этот аппарат используется при расчете торможения космических объектов, входящих в плотные слои атмосфер Земли и планет (например, метеоритов или возвращаемых на Землю космических кораблей и пр.). На этот вопрос легко ответить при выводе уравнений. Однако из этого вывода следует, что гипотеза сплошности среды справедлива, в частности, в том случае, когда характерный размер обтекаемого тела 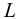(например, радиус сферического спутника) много больше длины свободного пробега атомов или молекул газа 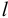, т.е. длины между последовательными их столкновениями.

Основные физические свойства жидкостей

Плотность

Плотность жидкости 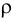, так же как любых других тел, представляет собой массу единицы объёма, и для бесконечно малого объёма жидкости 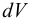массой 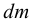может быть определена по формуле

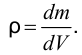
Для однородных жидкостей можно считать, что

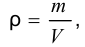
где 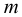— масса жидкости, кг; 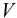— объём жидкости, 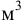. Единицы измерения плотности: 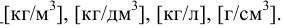Плотность жидкости зависит от температуры (рис. 4) и давления. Все жидкости, кроме воды, характеризуются уменьшением плотности с ростом температуры. Плотность воды имеет максимум при температуре 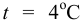и уменьшается при любых других температурах. В этом проявляется одно из аномальных свойств воды. Температура, при которой плотность воды максимальная, с увеличением давления уменьшается. Так, при давлении 14 МПа и при вода имеет максимальную плотность.

Плотность пресной воды равна 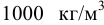, плотность солёной морской воды — 1020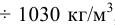, плотность нефти и нефтепродуктов —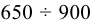 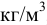, ртути — 13596 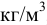, воздуха — 1,29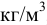

При изменении давления плотность жидкостей изменяется весьма незначительно. Плотность жидкости в большинстве случаев в расчётах можно принимать постоянной

Однако встречаются случаи, когда изменением плотности нельзя пренебрегать, гак как это может привести к значительным ошибкам в расчетах.

Удельный вес

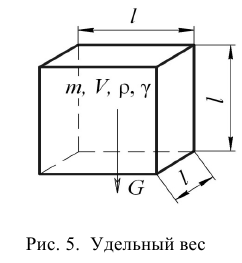
Удельным весом жидкости 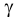называется вес единицы её объёма. Эта величина выражается формулой для бесконечно малого объёма жидкости (рис. 5) весом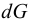

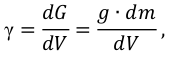
где 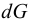— вес, Н;

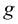— ускорение свободного падения, 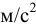. Для однородных жидкостей можно считать

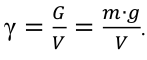
Удельный вес жидкости и плотность связаны соотношением

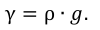
Единицы измерения:

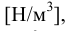
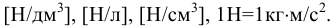
Значение ускорения свободного падения 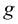на Земле изменяется от 9,831 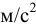на полюсах до 9,781 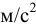на экваторе.

По этой причине удельный вес нельзя считать параметром вещества.

Иногда удобно использовать такую характеристику жидкости, которая называется «относительный удельный вес». Это отношение удельного веса рассматриваемой жидкости к удельному весу пресной воды

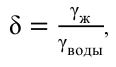
где 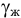— удельный вес жидкости, ;

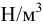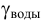— удельный вес воды, .

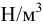Относительный удельный вес — величина безразмерная.

Сжимаемость жидкости

Сжимаемость жидкости — это свойство жидкостей изменять свой объём при изменении давления.

Сжимаемость характеризуется коэффициентом объёмного сжатия (сжимаемости) 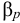, представляющим собой относительное изменение объёма жидкости 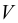при изменении давления 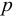на единицу

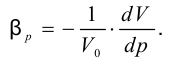
Знак минус в формуле указывает, что при увеличении давления объём жидкости уменьшается.

Единицы измерения:

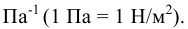
Перепишем определение 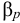в виде

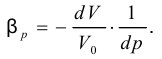
Обе части умножим на знаменатель и перенесём в левую часть

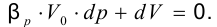
Учтём, что

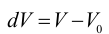
и подставим в предыдущее равенство

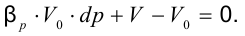
Выразив отсюда 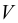, можно получить формулу для вычисления нового значения объёма при известном увеличении давления

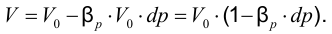
Если учесть, что все изменения объёма происходят при неизменной массе за счёт изменения плотности 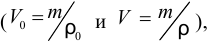можно получить формулу изменения плотности при изменении давления

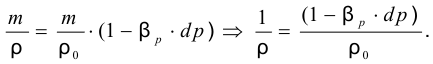
Откуда выразив 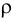, получим

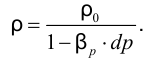
Изменение объёма 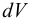, происходящее за счёт изменения плотности 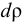при постоянной массе, можно записать в виде

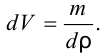
Подставив это в определение 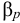определим коэффициент сжимаемости жидкости через изменение плотности

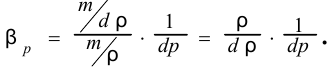
Отсутствие знака минус в этом выражении означает, что увеличение давления приводит к увеличению плотности.

Величина, обратная коэффициенту сжимаемости, или по-другому, коэффициенту объёмного сжатия 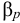, обозначается

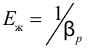
и называется объёмным модулем упругости жидкости.

Тогда предыдущая формула примет вид

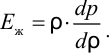
Это выражение называется законом Гука для жидкости.

Единицы измерения:

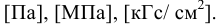
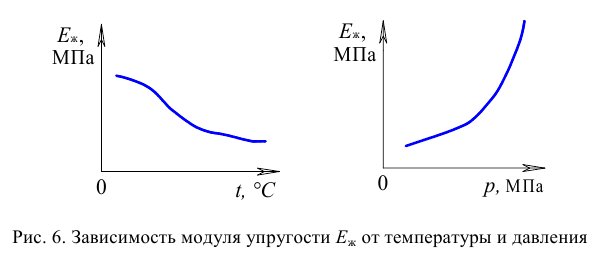
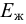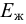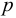Модуль упругости зависит от температуры и давления (рис. 6). Поэтому различают два модуля упругости: адиабатический и изотермический. Первый имеет место при быстротекущих процессах без теплообмена. Процессы, происходящие в большинстве гидросистем, происходят с теплообменом, поэтому чаще используется изотермический модуль упругости. Примерная форма зависимостей от и 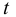представлена на графиках. Всё это говорит о том, что сжимаемость жидкости не вполне точно следует закону Гука.

Приведём несколько примеров значений модулей упругости.

Минеральные масла, используемые в технологических машинах с гидравлическим приводом, при 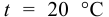имеют объёмные модули упругости 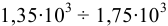МПа (меньшее значение относится к более легкому маслу), бензин и керосин — приблизительно 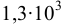МПа, глицерин — 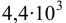МПа, ртуть — в среднем 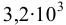МПа, вод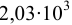а — МПа.

В практике эксплуатации гидравлических систем имеются случаи, когда вследствие действия того или иного возмущения в жидкости может значительно изменяться давление. В таких случаях пренебрежение сжимаемостью приводит к существенным погрешностям.

Известно, что скорость распространения звука с в однородной жидкости можно определить по формуле

Если вспомнить, что

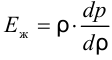
и подставить это значение в формулу скорости распространения звука, получим

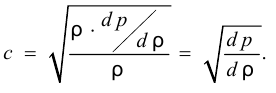
В этом случае изменение плотности жидкости, вызванное изменением давления, будет

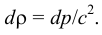
Если считать, что жидкость несжимаемая, то есть 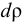= 0, то окажется, что скорость распространения звука в жидкости по приведённой формуле окажется бесконечной 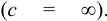. При использовании такого значения с в случае достаточно больших объёмов жидкости (озеро или нефтепровод) или быстрого изменения давления, например, при резком закрытии или открытии запорного устройства в трубопроводе, результаты расчётов окажутся существенно неточными. По этой причине в описанных условиях принимать жидкость несжимаемой недопустимо.

Температурное расширение жидкости

Температурное расширение жидкости проявляется в том, что она может изменять свой объем при изменении температуры. Это свойство характеризуется температурным коэффициентом объемного расширения, представляющим относительное изменение объема жидкости при изменении температуры на единицу (на 1°С) и при постоянном давлении

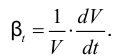
По аналогии со свойством сжимаемости жидкости можно записать

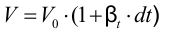
или через плотность

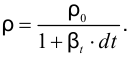
Изменение объёма при изменении температуры происходит за счёт изменения плотности.

Для большинства жидкостей коэффициент 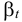с увеличением давления уменьшается. Коэффициент 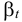с уменьшением плотности нефтепродуктов от 920 до 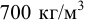увеличивается от 0,0006 до 0,0008; для рабочих жидкостей гидросистем 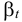обычно принимают не зависящим от температуры. Для этих жидкостей увеличение давления от атмосферного до 60 МПа приводит к росту 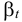примерно на 10-20 %. При этом, чем выше температура рабочей жидкости, тем больше увеличение коэффициента объемного расширения. Для воды с увеличением давления при температуре до 50 °С 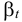растёт, а при температуре выше 50 °С уменьшается.

Растворение газов

Растворение газов — способность жидкости поглощать (растворять) газы, находящиеся в соприкосновении с ней. Все жидкости в той или иной степени поглощают и растворяют газы. Это свойство характеризуется коэффициентом растворимости .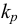

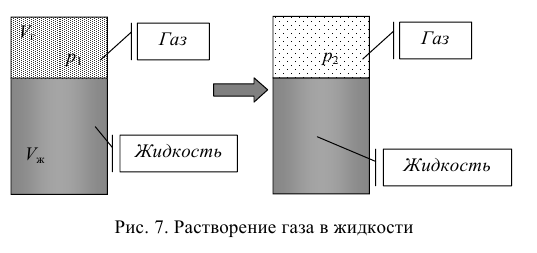
Если в закрытом сосуде жидкость находится в контакте с газом при давлении 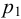, то газ начнёт растворяться в жидкости (рис. 7). Через какое-то время произойдёт насыщение жидкости газом и давление в сосуде изменится. Коэффициент растворимости связывает изменение давления в сосуде с объёмом растворённого газа и объёмом жидкости следующим соотношением

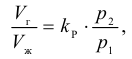
где 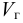— объём растворённого газа при нормальных условиях, 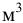; 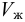— объём жидкост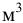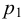и, ;

и 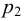— начальное и конечное давление газа, Па.

Коэффициент растворимости зависит от типа жидкости, газа и температуры.

При температуре 20°С и атмосферном давлении в воде содержится около 1,6% растворенного воздуха по объему (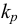 = 0,016). С увеличением температуры от 0 до 30°С коэффициент растворимости воздуха в воде уменьшается.

Коэффициент растворимости воздуха в маслах при температуре 20°С равен примерно 0,08 — 0,1. Кислород отличается более высокой растворимостью, чем воздух, поэтому содержание кислорода в воздухе, растворенном в жидкости, примерно на 50% выше, чем в атмосферном.

При уменьшении давления газ из жидкости выделяется. Процесс выделения газа протекает интенсивнее, чем растворение.

Кипение

Кипением называют образование большого числа пузырьков пара, всплывающих и лопающихся на поверхности жидкости при её нагревании. На самом деле эти пузырьки присутствуют в жидкости всегда, но их размеры растут, и они становятся заметны только при кипении. При нагревании жидкости в каждом из пузырьков процесс испарения ускоряется, а давление насыщенного пара растёт. Пузырьки расширяются и под действием выталкивающей силы Архимеда отрываются от дна, всплывают и лопаются на поверхности. При этом пар, наполнявший пузырьки, уносится в атмосферу. Поэтому кипение и называют испарением, происходящим во всём объёме жидкости.

Кипение начинается при той температуре, когда пузырьки газа имеют возможность расширяться, а это происходит, если давление насыщенного пара превышает атмосферное давление. Таким образом, температура кипения — это температура, при которой давление насыщенного пара данной жидкости равно атмосферному давлению. Пока жидкость кигшт, её температура остаётся постоянной.

Чем меньше атмосферное давление, тем при более низкой температуре кипит данная жидкость. Так, на вершине горы Эльбрус, где давление воздуха в два раза меньше нормального, обычная вода кипит не при 100°С, а при 82°С. Наоборот, если необходимо повысить температуру кипения жидкости, то её нагревают при повышенном давлении. На этом, например, основана работа скороварок, где еда, содержащая воду, может вариться при температуре более 100°С, не закипая.

Даже при нормальном атмосферном давлении разные жидкости кипят при разных температурах, например, ацетон — при 56°С, а этиловый спирт — при 78°С. Температура кипения железа — 2800°С, а вольфрама — 6000°С. То, что жидкости кипят при разных температурах, используется в получении различных нефтепродуктов из нефти путём её нагревания, т.к. весь бензин, например, испаряется из нефти раньше, чем масла и мазут.

Таким образом, жидкость можно довести до кипения повышением температуры до значений больших температуры кипения 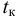при данном давлении или понижением давления до значений меньших давления насыщенных паров 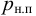жидкости при данной температуре. Образование пузырьков при понижении давления до давления насыщенных паров называется холодным кипением.

Давление насыщенных паров зависит от температуры и увеличивается с ее ростом. На рис. 8 представлена зависимость 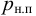воды от температуры.

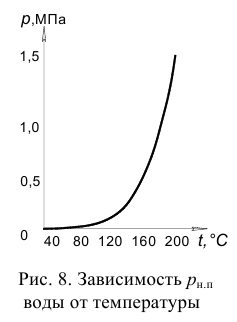
Жидкость, из которой удален растворенный в ней газ, называется дегазированной. В такой жидкости, кипение не возникает и при температуре большей температуры кипения при данном давлении.

Характеризовать испаряемость температурой кипения не всегда удобно, поскольку она меняется в зависимости от давления, поэтому давление насыщенных паров служит универсальной характеристикой.

Сопротивление растяжению жидкостей

Сопротивление растяжению жидкостей проявляется в способности жидкости противостоять растягивающим усилиям.

Сопротивление растяжению внутри капельных жидкостей по молекулярной теории может быть весьма значительным. Сопротивление растяжению в жидкости представляет собой результат сил сцепления между ее частицами. Академик Я. И. Френкель считал, что чистые жидкости могут выдерживать без разрыва очень большие растягивающие усилия, если они сводятся к всестороннему отрицательному давлению, исключающему возможность течения. Это подтверждено опытами. При опытах с тщательно очищенной и дегазированной водой в ней были получены кратковременные напряжения растяжения до 23 — 28 МПа. Однако технически чистые жидкости, содержащие взвешенные твердые частицы и мельчайшие пузырьки газов, не выдерживают даже незначительных напряжений растяжения. Поэтому в дальнейшем будем считать, что напряжения растяжения в капельных жидкостях невозможны.

Газы могут находиться в жидкости в растворенном и нерастворенном виде. Присутствие в жидкости нерастворенного газа в виде пузырьков существенно уменьшает модуль упругости жидкости, причем это уменьшение не зависит от размеров пузырьков воздуха. Динамическая вязкость жидкости с увеличением содержания в ней воздуха растет. Содержание нерастворенного воздуха в рабочих жидкостях гидросистем машин и механизмов, гак же как и в трубопроводах, подающих жидкость, может отрицательно повлиять на параметры работы технологических трубопроводов и гидросистем.

Вязкость

Вязкость — свойство жидкости оказывать сопротивление относительному сдвигу ее слоев. Вязкость — свойство противоположное текучести: более вязкие жидкости являются менее текучими и наоборот. Вязкость проявляется в том, что при относительном перемещении слоев жидкости на поверхностях их соприкосновения возникают силы сопротивления сдвигу, называемые силами внутреннего трения, или силами вязкости. В результате действия трения более быстро движущийся слой жидкости увлекает слой, движущийся медленнее, а медленнее движущийся слой «тормозит» соседний слой, движущийся быстрее. Силы внутреннего трения проявляются вследствие наличия межмолекулярных связей между слоями жидкости.

Рассмотрим слоистое прямолинейное движение жидкости в цилиндрической трубе круглого поперечного сечения (рис. 9). Жидкость движется кольцевыми концентрическими цилиндрическими слоями толщиной dy. Если рассмотреть то, как распределяются скорости различных слоев жидкости но сечению потока, то можно легко заметить, что чем ближе сечение к стенкам трубы, тем меньше скорость движения частиц, а чем оно ближе к оси трубы, тем скорость больше. При ламинарном течении у стенок потока скорость равна нулю. Иллюстрацией этого является рисунок, гак называемой струйной модели потока. На рисунке применены следующие обозначения: и скорость слоя жидкости, м/с; у — расстояние между соседними слоями жидкости, м.

Если в равномерно движущемся потоке жидкости рассмотреть два соседних слоя с ординатам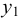и и 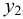, расположенными на расстоянии 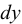друг от друга, и скорость первого из них обозначить 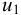, а скорость другого 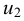(см. рис. 9), то разница скоростей составит 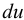. Тогда можно записать

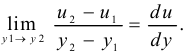
Эта величина называется градиентом скорости по сечению потока или поперечным градиентом скорости. Он показывает, как меняются скорости слоев жидкости по сечению потока.

Если между соседними слоями жидкости выделить некоторую площадку 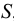, то согласно гипотезе Ньютона

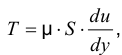
где 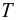— силы вязкого трения, Н;

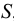— площадь трения или соприкосновения слоев, ;

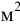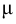-динамический коэффициент вязкого трения, .

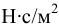Динамический коэффициентом вязкости равен

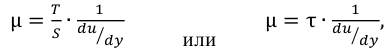
где 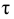— касательные напряжения, возникающие в жидкости под действием силы трения, Па.

Физический смысл коэффициента вязкого трения — число, равное силе трения, развивающейся на единичной поверхности при единичном градиенте скорости.

Единицы измерения:

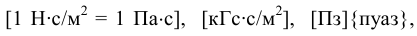
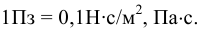
На практике чаще используется кинематический коэффициент вязкости, названный так потому, что в его размерности отсутствует обозначение силы. Этот коэффициент представляет собой отношение динамического коэффициента вязкости жидкости к её плотности

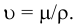
Единицы измерения:

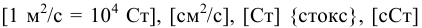
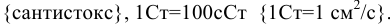
Анализ свойства вязкости

Для капельных жидкостей вязкость зависит от температуры 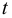и давления 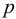, однако последняя зависимость проявляется только при больших изменениях давления, порядка нескольких десятков МПа.

Для капельных жидкостей увеличение температуры приводит к снижению сил вязкостного трения. Для газов же рост температуры, напротив, вызывает увеличение вязкости.

В жидкостях, где расстояния между молекулами много меньше, чем в газах, вязкость обусловлена в первую очередь межмолекулярным взаимодействием, ограничивающим подвижность молекул. В жидкости молекула может проникнуть в соседний слой лишь при образовании в нём полости достаточной для перескакивания туда молекулы. На образование полости (на «рыхление» жидкости) расходуется гак называемая энергия активации вязкого течения. Энергия активации уменьшается с ростом температуры и понижением давления. В этом состоит одна из причин резкого снижения вязкости жидкостей с повышением температуры и роста её при высоких давлениях.

Все молекулы газа постоянно находятся в беспорядочном движении. Когда из-за наличия потока происходит массивное движение, то это оказывает влияние и на обычное, хаотичное, перемещение. Затем из-за столкновений молекул этот процесс распространяется во всем объеме флюида. На интенсивность беспорядочного движения влияет температура: чем сильнее такое движение, тем выше сопротивление массивному движению потока.

Теоретический анализ, базирующийся на этих простых утверждениях, показывает, что вязкость газа пропорциональна квадрату его абсолютной температуры. Эффект передачи момента при столкновении молекул жидкости перекрывает феномен взаимодействия сил находящихся рядом молекул. Поэтому температура оказывает обратный эффект на вязкость газов и жидкостей.

Зависимость коэффициента динамической вязкости от температуры выражается формулой вида

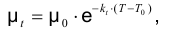
где 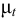— коэффициент динамической вязкости при заданной температуре, Пас;

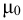— коэффициент динамической вязкости при известной температуре, Пас;

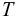— заданная температура, °С; 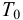— температура, при которой измерено значение 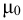°С;

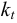— коэффициент равный 0,02-0,03.

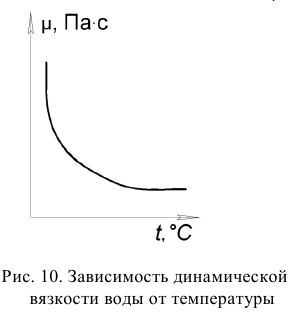
На рис. 10 представлена зависимость динамической вязкости воды от температуры.

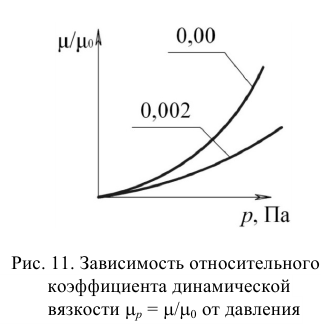
Зависимость относительного коэффициента динамической вязкости 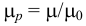от давления (рис. 11) описывается формулой

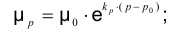
где 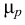— коэффициент динамической вязкости при заданном давлении, Пас;

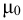— коэффициент динамической вязкости при известном давлении (чаще всего при нормальных условиях), Па с; 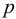— заданное давление, Па;

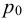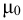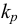— давление, при которой измерено значение , Па; — коэффициент равный 0,002-0,003.

Формула Сазерленда может быть использована для определения вязкости идеального газа в зависимости от температуры

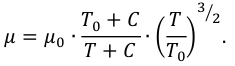
где 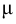— динамическая вязкость в (Па с) при заданной температуре ;

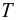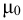— контрольная вязкость в (Па с) при некоторой контрольной температуре ;

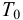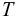— заданная температура в Кельвинах; 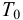— контрольная температура в Кельвинах;

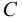— постоянная Сазерленда для того газа, вязкость которого требуется определить.

Эту формулу можно применять для температур в диапазоне 0° < 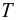< 555°К и при давлениях менее 3,45 МПа с ошибкой менее 10%, обусловленной зависимостью вязкости от давления.

Влияние давления на вязкость жидкости проявляется только при высоких давлениях. Для примера приведём значения кинематического коэффициента вязкости 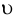для некоторых жидкостей: масла индустриальные (по ГОСТ 20799-75) при температурах 50 С: И-5А — 4-5 сСт, И-12А — 10-14 сСт, И-40А — 35-45 сСт; вода пресная при 20 С 0,0101 Ст; ртуть при температуре 15 С — 0,0011 Ст, сталь жидкая при 1550 С -0,0037 Ст.

Вязкость жидкости — это свойство, проявляющееся только при движении жидкости, и не влияющее на покоящиеся жидкости. Вязкое трение в жидкостях подчиняется закону трения, принципиально отличному от закона трения твёрдых тел, гак как зависит от площади трения и скорости движения жидкости.

Вязкость жидкостей зависит от химической структуры их молекул. В рядах сходных химических соединений (насыщенные углеводороды, спирты, органические кислоты и т.д.) вязкость изменяется закономерно — возрастает с возрастанием молекулярной массы. Высокая вязкость смазочных масел объясняется наличием в их молекулах циклов. Две жидкости различной вязкости, которые не реагируют друг с другом при смешивании, обладают в смеси средним значением вязкости. Если же при смешивании образуется химическое соединение, то вязкость смеси может быть в десятки раз больше, чем вязкость исходных жидкостей.

При течении жидкости или газа наличие внутреннего трения приводит к процессу диссипации (рассеяния) энергии. Существо процесса диссипации состоит в том, что часть кинетической энергии движущейся жидкости необратимо переходит в теплоту и вызывает нагревание жидкости. Если вязкость жидкости или ее скорость невелики, то нагревание будет незначительным. В дальнейшем в основном будут рассматриваться процессы, для которых выделяемая теплота трения незначительна и ею можно пренебречь.

Жидкости, которые подчиняются описанному закону жидкостного трения Ньютона, называются ньютоновскими жидкостями. Однако есть жидкости, трение в которых описывается другими закономерностями.

Неньютоновские жидкости

Особенностью ньютоновских жидкостей является полное отсутствие трения покоя. Однако существуют жидкости (растворы полимеров, коллоидные суспензии, строительные растворы, пищевые и кормовые смеси и т. п.), для которых связь между касательным напряжением 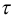и поперечным градиентом скорости не подчиняется закону Ньютона. Такие жидкости называются неныотоновскими или аномальными, и отличаются от ньютоновских наличием касательного напряжения в состоянии покоя .

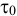Например, касательные напряжения подчиняются закону

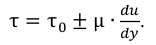
Такие жидкости называются вязкоиластичными, и движение их слоев начинается лишь после того, как будет преодолено напряжение сдвига покоя .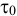

Для других неныогоновских жидкостей динамическая вязкость может зависеть от градиента скорости, времени и гак далее. Эта зависимость может иметь, например, следующий вид

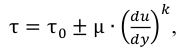
где 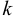— коэффициент, который может зависеть от скорости, времени, температуры, давления и некоторых других факторов.

Возможно эта страница вам будет полезна:

Задачи по гидравлике

Определение вязкости жидкости

Вязкость жидкости в условных градусах Энглера определяется экспериментально с помощью приборов, которые называются вискозиметрами. Для определения условной вязкости необходимо время истечения 200 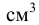исследуемой жидкости 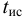через отверстие 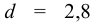мм разделить на время истечения такого же объема дистиллированной воды 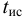при температуре 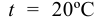через то же отверстие. Полученное выражение называют градусами Энглера и обозначают .

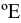Связь между условной коэффициентом вязкости 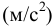эмпирическим соотношением Убеллоде

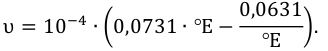
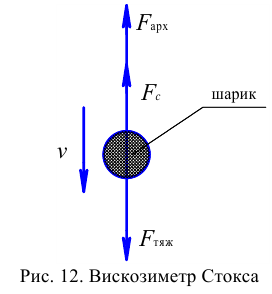
Примером может служить вискозиметр Стокса (рис. 12). Его работа основана на следующем методе.

Связь вязкостью и кинематической выражается

В прозрачную трубку с жидкостью помещается шарик, плотность которого выше плотности жидкости. Шарик медленно опускается в вязкой жидкости с постоянной скоростью 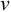. На шарик будут действовать: во-первых, сила тяжести

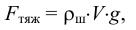
во-вторых, выталкивающая (архимедова) сила

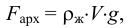
в-третьих, сила Стокса, порождаемая вязким трением на поверхности шарика

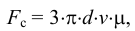
где 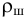— плотность материала шарика ;

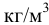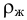— плотность жидкости, 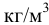; 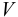— объём шарика, 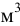; 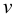— скорость падения шарика, м/с; 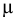— динамический коэффициент вязкости, Па с; 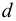— диаметр шарика, м.

Так как скорость тела постоянна, по второму закону Ньютона можно записать

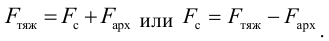
Объём шарика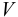

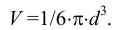
Подставляя полученные выражения в уравнение сил, действующих на шарик, получим

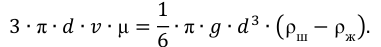
Выразив из последней формулы 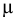, будем иметь выражение для определения динамического коэффициента вязкости

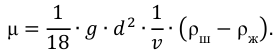
Если измерить время опускания шарика на определённую, заранее измеренную глубину, то нетрудно определить вязкость любой жидкости.

Эксплуатационные свойства жидкостей

Кроме рассмотренных физических свойств жидкостей при их использовании в технологических машинах нужно учитывать и другие характеристики. Они не влияют на математическое описание гидравлических явлений, но оказываются существенными при эксплуатации гидросистем. Требования к таким свойствам определяются, прежде всего, целью, с которой жидкость применяется в технологической машине. В гидроприводе жидкость выполняет несколько различных функций. Во-первых, это функция рабочего тела, обеспечивающего перенос энергии в гидросистеме, поэтому её называют рабочей жидкостью, в гидроприводах тормозов — тормозными жидкостями. Во-вторых, рабочая жидкость является смазочным и охлаждающим веществом. В системах смазки их называют маслами, в системах охлаждения — охлаждающими или смазочно-охлаждающими жидкостями (СОЖ). В этом случае они обеспечивают уменьшение сил трения в парах трения. В-третьих, жидкость является средой, удаляющей из гидросистемы продукты износа. В-четвёртых, смазочно-охлаждающие жидкости обеспечивают защиту деталей от коррозии.

Комплекс физико-химических свойств рабочих жидкостей должен наилучшим образом обеспечивать их основную и дополнительные функции. Рабочие жидкости гидросистем должны обладать следующими дополнительными свойствами.

Антифрикционные (смазывающие) свойства заключаются в способности жидкости уменьшать силы трения между движущимися деталями. Данное свойство обеспечивается посредством добавления различных модификаторов и присадок.

Стабильность вязкости состоит в минимальной зависимости вязкости от температуры в требуемом температурном диапазоне. Вязкость жидкости должна быть оптимальна, то есть должна обеспечивать хорошие смазывающие свойства при минимальных утечках через неплотности и зазоры в гидросистеме. Это свойство существенным образом зависит ог относительных скоростей движения подвижных частей.

Температура кипения должна быть высокой, что обеспечивает работоспособность и стойкость жидкости в большом температурном диапазоне.

Устойчивость к механической и химической деструкции и к окислению должна быть высокой в условиях применяемого температурного режима, а также в течение максимально длительного срока службы.

Модуль объемной упругости должен максимально высоким.

Коэффициенты теплопроводности и удельной теплоемкости должны быть высокими, что обеспечивает интенсивный отвод тепла из гидросистемы и повышает точность её работы.

Коэффициент теплового расширения должен быть небольшим, так как это также приводит к увеличению точности работы гидросистемы.

Экологическая безопасность жидкости и продуктов её разложения заключается в недорогой возможности переработки, повторного использования или утилизации после окончания срока эксплуатации.

Температурой застывания называют такую наиболее высокую температуру, при которой поверхность уровня масла, залитого в стандартную пробирку, не перемещается при наклоне пробирки на 45° в течение 5 мин. Эта температура характеризует жидкость с точки зрения сохранения текучести, а следовательно, возможности транспортировки и слива в холодное время года.

Температура застывания масла должна быть не менее чем на 10 17°С ниже наименьшей температуры окружающей среды, в условиях которой будет работать гидросистема.

Температурой замерзания называют температуру начала кристаллизации, т.е. температуру, при которой в жидкости образуется облачко из мельчайших кристаллов. При этом не должно быть расслаивания жидкости и выделения из нее составных компонентов.

Жидкость не должна содержать легкоиспаряющиеся компоненты, испарение которых может привести при продолжительной эксплуатации к загустению жидкости.

Огнестойкость жидкостей выражается в том, что жидкость не должна быть причиной возникновения или распространения пожара.

С точки зрения огнестойкости жидкости характеризуются температурами вспышки, воспламенения и самовоспламенения. Под температурой вспышки понимается минимальная температура, при которой над поверхностью жидкости образуется количество пара, достаточное для возникновения кратковременной вспышки. Температурой воспламенения называется такая температура, при которой количество выделяющегося пара таково, что горение продолжается после удаления источника огня. Температурой самовозгорания называется такая температура, при которой жидкость или ее пар вспыхивает при контакте с воздухом без внешнего источника воспламенения.

Температура воспламенения масел на нефтяной основе находится в пределах 180 — 230°С, а температура самовозгорания от 260 — 370°С и выше.

Негорючесть во многих случаях является решающим свойством при выборе типа рабочей жидкости. В гидросистемах, расположенных близко к источникам тепла или огня, необходимы негорючие жидкости.

Более высокой пожарной безопасностью, по сравнению с минеральными, обладают синтетические жидкости. Они практически не горят при возможных высоких температурах и не распространяют огня. При работе с минеральными маслами при температуре выше 70°С необходимо устранять контакт с воздухом. Для этого баки при 70°С и выше необходимо заполнять инертным газом (азотом, аргоном или гелием). Этого же эффекта можно достичь механическим разделением газовой и жидкостной сред.

Встречаются случаи, когда важными являются изолирующие и диэлектрические свойства жидкости.

Большинство жидкостей для гидросистем — хорошие изоляторы. Такое свойство позволяет помещать в них электрические агрегаты и их элементы (соленоиды, обмотки электродвигателей и пр.) без дополнительной изоляции. Однако в этом случае в жидкостях не должно быть металлических присадок и металлических продуктов износа. Они также не должны содержать воду.

Воздействие жидкости на резиновые детали. Важным свойством рабочих жидкостей для гидросистем является воздействие их на материалы конструктивных элементов, и, в частности, на резиновые детали гидроагрегатов, которые используются в качестве уплотнений. Изменение их свойств, происходящее под воздействием жидкости, сопровождается нарушением герметичности и другими ошибками в работе гидросистем.

Ни одна рабочая жидкость не обладает абсолютной инертностью. Поэтому важно, чтобы она не критично ухудшала основные качества материала уплотнительных устройств. В результате длительного контакта рабочей жидкости с резиновыми деталями могут изменяться их объем, вес, прочность и другие механические свойства деталей. Особо следует отметить влияние на резину синтетических жидкостей, одни из которых вызывают либо чрезмерное набухание уплогнительного материала, либо, наоборот, значительную его усадку.

Цена рабочей жидкости должна быть по возможности невысокой.

Перечисленные свойства гидравлических рабочих жидкостей, к сожалению, не носят постоянный характер. В процессе работы гидросистем происходит изменение их характеристик.

Изменение характеристик рабочих жидкостей

Наиболее существенным фактором, влияющим на свойства рабочих жидкостей, является количество и состав частиц, загрязняющих эту жидкость.

Загрязнение рабочих жидкостей гидросистемы может происходить в следующих случаях:

• во время поставки жидкостей, хранения и заправки их в гидросистему,
• в процессе изготовления, сборки и испытания элементов гидросистемы,
• в процессе эксплуатации,
• за счёт распада самой жидкости под действием различных факторов.

Загрязнение во время поставки, хранения и заправки

Различные присадки и добавки, предназначенные для улучшения эксплуатационных свойств жидкости в процессе транспортировки и хранения, могут выделяться из жидкости, превращаясь в загрязняющие вещества. При длительном хранении в условиях положительных температур в маслах могут развиваться колонии микроорганизмов, водорослей и грибков. Размер отдельных грибков и бактерий, а также их спор составляет, как правило, 1 — 2 мкм, однако может достигать и 10 мкм. В основном их наблюдают на границе масло — вода. Непрерывно идёт процесс окисления масла. Активность этого процесса повышается с увеличением температуры и при наличии в масле эмульгированного воздуха. Катализатором окисления являются частицы износа из чёрных и цветных металлов. При окислении в масле образуются растворимые и нерастворимые продукты, которые способствуют его сгущению и могут, в конечном счёте, выпадать в виде осадка на детали гидроаппаратов и гидромашин. Мельчайшие нерастворимые продукты окисления коагулируют и укрупняются. Замечены случаи «самопроизвольного» увеличения размеров частиц загрязнений в герметически закрытых сосудах. Например, если при заправке в жидкости были зафиксированы частицы не более 10 мкм, то со временем обнаруживались частицы размером 25 — 200 мкм в виде рыхлых образований. Быстрый рост размера частиц происходит в жидкости, подвергающейся тряске при транспортировке. Жидкость может загрязняться частицами пыли из воздуха. Пыль поступает в баки через систему наддува и дренажа, через заливные горловины при «открытой» заправке баков. Пыль всегда присутствует в атмосфере. В одном литре воздуха число пылинок может изменяться от 10 до Предельная крупность частиц ныли в воздухе составляет 50 мкм, основную массу пыли составляют пылинки размером менее 10 мкм. В их составе:

• до 80% — кварц твёрдостью 7 единиц по десятибалльной шкале

(Мооса),

• до 17% — окись алюминия с твёрдостью 9 единиц,
• полевой шпат с твёрдостью 6 — 6,5 единиц,
• другие компоненты.

Для сравнения: твёрдость алмаза по десятичной шкале — 10, железа — 4,4, меди — 3,0, алюминия — 2,9.

Таким образом, большая доля частиц пыли соизмерима с зазорами в подвижных узлах гидроагрегатов, а твёрдость некоторых компонентов загрязнений значительно превосходит твёрдость материалов сопрягаемых деталей.

Загрязнение в процессе изготовления, сборки и испытания

Большое количество частиц загрязнения остаётся в гидросистеме и её элементах после изготовления и ремонта. Это песок, попадающий при литье; пыль, осевшая на стенках; окалина от сварки, ковки или термической обработки; остатки механической обработки деталей; заусенцы от трубопроводов; волокна ветоши, остающиеся после протирки. Притирочные иасгы, применяемые при доводке гидроагрегатов, образуют смешанные с парафином, стеарином, воском и др. абразивные зёрна (карбиды бора и кремния, белый электрокорунд, алмазная пыль), твёрдость которых превышает твёрдость большинства конструкционных материалов. Паста при обработке деталей обычно накапливается в глухих ответвлениях системы и при её работе постепенно вымывается, циркулируя вместе с рабочей жидкостью.

Загрязнение в процессе эксплуатации

Наибольшее количество частиц загрязнения попадает в рабочие жидкости в процессе эксплуатации гидросистемы. За счёт износа её элементов рабочие жидкости загрязняются непрерывно самыми различными видами загрязнителей — ржавчиной, резиной, металлом, абразивными частицами, волокнистыми частицами, краской, пылью. Особенно интенсивный износ наблюдается в парах трения, дроссельных элементах, рабочих камерах гидромашин, распределительных устройствах плунжерных насосов и т.д. Продукты износа трущихся деталей поступают в жидкость непрерывно. При микроанализе проб жидкости было установлено, что размер металлических продуктов износа, генерируемых в рабочую жидкость, составляет от 1 до 10 мкм.

Совместное воздействие влаги, кислорода воздуха и рабочей жидкости может вызвать на поверхности деталей, трубопроводов, баков образование ржавчины и шелушение покрытий. Частицы ржавчины выпадают в виде осадка частиц микронных размеров. Этому способствует вибрация конструкции и пульсации давления.

Кроме того, загрязнения в жидкость попадают при обслуживании системы, при небрежном монтаже агрегатов, шлангов и трубопроводов, через незаглушенные соединительные узлы, из-за загрязнённости инструментов, заправочных средств, одежды обслуживающего персонала.

Источником загрязнения топлив и масел в некоторых случаях могут служить также сами фильтры, предназначенные для очистки жидкости. В процессе работы фильтрующие элементы частично разрушаются и их компоненты вымываются потоком жидкости. Такого типа загрязнения наблюдаются у всех фильтров с волокнистыми наполнителями, изготовленными, например, из бумаги, шерсти, войлока, целлюлозы, стекловолокна и т.п. Кроме того, при использовании волокнистых наполнителей, которые могут изменять пористость при увеличении перепада давлений во время гидроударов и пульсаций давления, задержанные фильтром частицы загрязнения, медленно проходят через фильтроэлемент и вновь попадают в рабочую жидкость.

Распад жидкости под действием различных факторов

Рабочая жидкость в процессе хранения, транспортировки, заправки и эксплуатации подвергается воздействию различных видов энергии, вступает в контакт с различными видами материалов (металлами, полимерами, кислотами, водой и т.д.), многие из которых являются катализаторами химических процессов. Постоянно воздействующим фактором является тепловая энергия, иногда радиационная и электрическая. Эти виды энергии определяют интенсивность статических процессов старения. Старением называют изменение свойств вещества во времени. В динамических условиях, в дополнение к этим видам энергии, на масло действуют механическая энергия при сжатии и разрежении, волновая механическая энергия при вибрациях, звуковых и ультразвуковых колебаниях. В результате этих воздействий в рабочей жидкости происходит комплекс физико-химических изменений, которые можно разделить на три группы.

1. Изменения физического характера: испарение компонентов масла, проникновение в жидкость продуктов изнашивания, растворение газов, воды и компонентов эластомеров, изменение количественного состава присадок за счёт образования сорбционных плёнок на поверхностях контактирующих деталей.
2. Изменения химического характера: окисление углеводородов базового масла и присадок вследствие присутствия в масле воды и водных растворов, реакции присадок масла с материалами гидросистемы и другие химические процессы
3. Изменения механохимического характера: участие масла в процессах трения, перемешивания, а также стимулирующее влияние механических воздействий на химические реакции.

Последствия загрязнения рабочей жидкости

Надежность работы гидропривода находится в непосредственной зависимости от чистоты рабочей жидкости. В большинстве случаев наблюдаются следующие нарушения работы и повреждения, вызванные загрязнением:

• затруднённость движения или полная остановка,
• ошибки позиционирования привода,
• отклонения ог заданной скорости движения гидродвигателя,
• скачкообразность движения привода при плавном изменении управляющего сигнала,
• уменьшение жёсткости системы из-за увеличения утечек в гидроагрегатах,
• порча поверхности штоков и валов гидродвигателей,
• порча поверхности сёдел клапанов.

Эти повреждения значительно ухудшают качество выполняемых оборудованием технологических операций и ведут к производству бракованных изделий. Кроме этого, наличие загрязнения в жидкости необходимо учитывать при разработке элементов гидросистем. Например: силы, требуемые для перемещения плунжеров распределителей, измеряемые десятыми долями Ныотона, могут при наличии загрязнения возрасти в согни раз, вызвав нарушение нормальной работы гидросистемы и даже выход из строя отдельных её участков. Чтобы гарантировать надёжную работу, для преодоления сил трения плунжеров применяют электромагниты с большим тяговым усилием, достигающим 150 Н. Такие устройства имеют большие размеры и массу и малый срок службы, так как большие инерционные силы, развиваемые якорем при его втягивании, быстро разбивают электромагнит, что ведёт к увеличению затрат на обслуживание системы. В то же время, большие пусковые токи требуют мощных контактных устройств в системах электропитания.

Загрязнения в жидкости существенно влияют также на срок службы гидроаппаратов и гидромашин. Жидкость со взвешенными твёрдыми частицами при течении с большой скоростью, достигающей в некоторых участках систем 300 м/с, притупляет, подобно абразивной эмульсии, кромки распределительных отверстий. От этого с течением времени увеличиваются зазоры, уменьшаются перекрытия, изменяются коэффициенты расхода и сопротивления сопел и точных (калиброванных) отверстий.

Из вышеизложенного следует, что необходимо постоянно контролировать степень чистоты рабочей жидкости во время заправки и работы оборудования, гак как это может способствовать своевременному предупреждению отказов в работе гидросистем. Для каждой гидросистемы в зависимости от её назначения и выполняемых функций, планируемой надёжности и срока службы аппаратуры должна быть назначена определённая степень чистоты рабочей жидкости.

Определение класса чистоты рабочей жидкости.

В большинстве случаев для оценки степени чистоты жидкости используются следующие показатели:

• масса частиц загрязнения в единице объема жидкости,
• объем механических включений в единице объема жидкости,
• количество частиц разных размеров в единице объема жидкости.

Степень чистоты рабочей жидкости определяется на основе

нескольких стандартов: ГОСТ 6370-59, 10227-62, 10577-63 и других. Приведем пример некоторых из них. По ГОСТ 6370-59 жидкость считается чистой, если содержание загрязняющих частиц в ней не превышает 0,005%, что составляет 50 мг/л. Общей массой частиц загрязнения нельзя до конца охарактеризовать степень загрязненности, гак как при одинаковой массе количество частиц может сильно изменяться.

В ГОСТ 17216-2001 загрязненность определяется иначе. Этот стандарт устанавливает 19 классов чистоты рабочей жидкости, каждому из которых соответствует определенное число частиц различного размера, содержащихся в 0,1 л жидкости.

Международная ассоциация транспортной авиации рекомендует использовать в качестве рабочей среды жидкость с частицами загрязнения не больше 5 мкм и с ограниченным числом меньших размеров. По проекту международной организации ИСО/ТК 131 классы чистоты жидкости устанавливаются по размерам частиц более 15 мкм.

Существуют и другие методы определения загрязненности рабочей среды. Во всех случаях контроля чистоты жидкость должна быть перемешана, либо проба должна сниматься не позже одной минуты после остановки гидросистемы. Приспособление для извлечения пробы должно исключать проникновение в пробу частиц загрязнения извне как во время взятия, гак и во время транспортирования, что обеспечивает проведение максимально точного анализа. Кроме перечисленных существует ещё целый ряд требований к проведению подобных анализов.

Метод анализа степени чистоты рабочей жидкости ориентирован на ГОСТ 17216-2001, который учитывает количество и размер частиц загрязнения в 100 жидкости и классифицирует жидкость по 19-ти классам чистоты. Обычно такой анализ проводится следующим образом. С помощью специального заборного устройства (рис. 13)

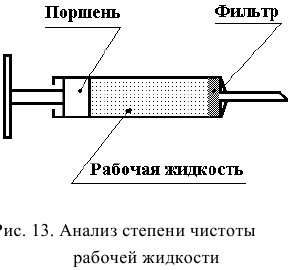
набирается проба жидкости в объёме 100 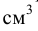. Эта проба проходит через фильтр, на котором, остаются частицы загрязнения. После этого с помощью микроскопа проводится подсчёт частиц, осевших на фильтре с учетом их размеров.

Такой метод — очень длительный и трудоёмкий процесс. При его использовании субъективная погрешность оператора может достигать 100%, а время, затрачиваемое на анализ одной пробы (одного фильтро-элеменга), может составлять нескольких часов.

Возможно эта страница вам будет полезна:

Решение задач по гидравлике

Гидростатика

Гидростатика — раздел гидромеханики, изучающий законы равновесия неподвижной жидкости, находящейся под действием внешних сил.

Вследствие действия этих сил внутри жидкости возникают напряжения сжатия, которые в гидравлике называются давлением и обозначаются буквой 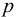. В гидростатике силы, действующие на жидкость, принимаются не зависящими от времени. С учётом этого положения можно считать, что напряжения, возникающие в жидкости под действием внешних сил, зависят только от координат точки 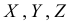в жидкости. Таким образом, основными задачами гидростатики являются определение давления в жидкости как функции координат

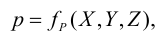
а также определение сил, действующих со стороны жидкости на твёрдые стенки.

Силы, действующие в жидкости

В гидравлике, как правило, жидкость рассматривают как непрерывную среду, отвлекаясь от ее молекулярного строения.

Вследствие текучести (подвижности частиц) в жидкости действуют только силы, распределенные по ее объему (массе) или поверхности. В точке к жидкости приложить силу невозможно. Проведите мысленный эксперимент. Нажмите острием иглы на твердое тело, и вы почувствуете, что оно сопротивляется проникновению иглы. Попробуйте воздействовать той же иглой на поверхность воды или иной жидкости. Игла погружается в жидкость беспрепятственно, то есть, силу в точке приложить к жидкости не удалось. Таким образом, силы, действующие на объемы жидкости извне, подразделяют на массовые и поверхностные.

Массовые силы в соответствии со вторым законом Ньютона пропорциональны массе жидкости или, для однородной жидкости, — ее объему. К ним относятся сила тяжести, силы инерции, электромагнитные силы.

Поверхностные силы непрерывно распределены по поверхности жидкости и при равномерном их распределении пропорциональны площади этой поверхности. Это силы, действующие на жидкость, со стороны твердых тел, газа или других объемов жидкости. По третьему закону Ньютона точно с такими же силами жидкость воздействует на окружающие ее тела.

В общем случае поверхностная сила 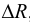действующая на элементарно малую площадку 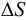, направлена под некоторым углом к площадке и ее можно разложить на две составляющие: нормальную 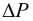(перпендикулярную площадке) и тангенциальную 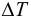(направленную вдоль площадки). Величину 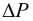называют силой давления, a 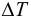— силой трения (рис. 14).

Единичная поверхностная сила, называемая напряжением этой поверхностной силы, раскладывается на нормальные и касательные (тангенциальные) напряжения.

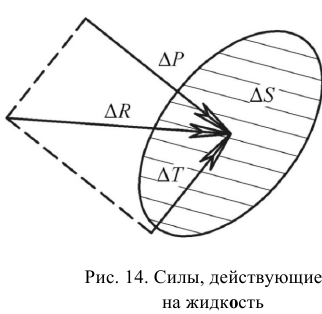
Нормальное напряжение называется гидромеханическим (а в случае покоя жидкости -гидростатическим) давлением, или просто давлением и обозначается 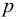, а при равномерном распределении

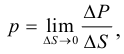
поверхностей силы по площадке

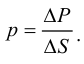
Давление — напряжение, возникающее в жидкости под действием сжимающих сил. В любом случае причиной возникновения давления является внешняя сила, приложенная к жидкости.

Касательные напряжения (напряжения трения) 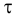определяются аналогично

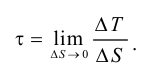
Массовые силы характеризуются ускорением массовых сил. Если на элементарно малый объем жидкости 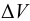(рис. 15) массой 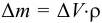действует массовая сила 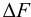, то ускорение этой силы в некоторой точке 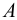при стягивании объема в точку будет равно

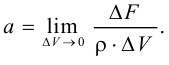
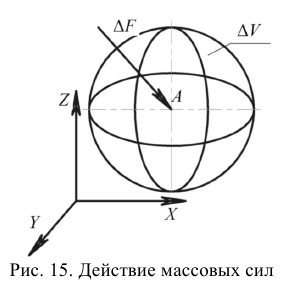
Ускорение массовых сил в проекциях на соответствующие оси можно представить как

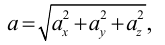
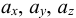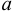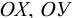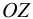где — проекции ускорения на оси и соответственно, .

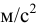Силы поверхностного натяжения

Молекулы жидкости притягиваются друг к другу с определённой силой. Причём внутри жидкости силы, действующие на любую молекулу, уравновешиваются (рис. 16), гак как со всех сторон от неё находятся одинаковые молекулы, расположенные на одинаковом расстоянии.

Однако молекулы жидкости, находящиеся на границе (с газом, твердым телом или на границе двух несмешивающихся жидкостей), оказываются в неуравновешенном состоянии, так как со стороны другого вещества действует притяжение других молекул, расположенных на других от нее расстояниях. Возникает преобладание какой-то силы. Под влиянием этого воздействия поверхность жидкости стремится принять форму соответствующую наименьшей площади. Если силы внутри жидкости больше наружных сил, то поверхность жидкости стремится к сферической форме. Например, малые массы жидкости в воздухе стремятся к шарообразной форме, образуя капли.

Может иметь место и обратное явление, которое наблюдается как явление капиллярности. В трубах малого диаметра (капиллярах) наблюдается искривление свободной поверхности, граничащей с газом или с парами этой же жидкости. Если поверхность трубки смачивается, свободная поверхность жидкости в капилляре — вогнутая. Если нет смачивания, свободная поверхность — выпуклая, как при каплеобразовании. Во всех этих случаях силы поверхностного натяжения обуславливают дополнительные напряжения 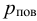в в жидкости. Величина этих напряжений определяется формулой

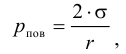
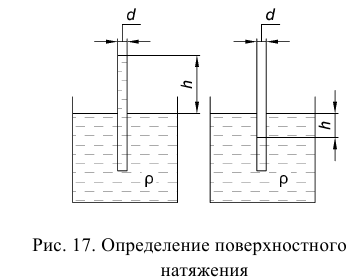
где 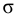— коэффициент поверхностного натяжения, Н/м; 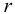— радиус сферы, которую принимает жидкость, м.

Эти дополнительные напряжения легко наблюдать, если в сосуд с жидкостью погрузить капилляр (рис. 17). В этом опыте возможны два варианта. В первом случае жидкость за счёт поверхностных сил поднимется по капилляру на некоторую высоту. Тогда говорят капиллярном поднятии, и наблюдается явление смачивания.

Во втором варианте жидкость опускается в капилляре ниже уровня жидкости в сосуде. Такое явление называют капиллярным опусканием, которое происходит при несмачивании.

В обоих случаях величина 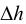пропорциональна дополнительному напряжению, вызванному в жидкости поверхностными силами. Она равна

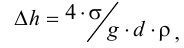
где 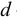— диаметр капилляра, м;

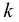— коэффициент пропорциональности, который выражается следующей зависимостью

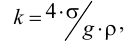
и зависит от тина и состояния жидкости. Например, при 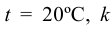спирта составляет 11,5, ртути — 10,15, а воды — 30.

Поднятие воды в капиллярах почвы и грунтов является важным фактором в распространении воды. Высота капиллярного поднятия в грунтах изменяется от нуля (галечники) почти до 5 м (глины). При этом с увеличением минерализации воды высота капиллярного поднятия увеличивается.

Поверхностное натяжение и капиллярные эффекты определяют закономерности движения жидкости в условиях невесомости.

Свойства гидростатического давления

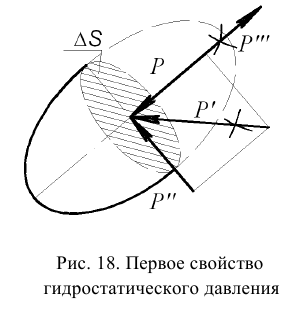
Первое свойство гидростатического давления формулируется следующим образом: давление (как и сила давления) всегда направлено по внутренней нормали к площадке действия.

Доказывается первое свойство путём рассуждений методом «от противного». Рассмотрим объем жидкости, находящейся в состоянии покоя (рис. 18) (в общем случае относительного покоя), когда жидкость в резервуаре, который движется с ускорением относительно Земли, неподвижна по отношению к резервуару.

Рассечем объем, занимаемый жидкостью, произвольной плоскостью на две части, и отбросим одну из частей объема, например правую верхнюю. Чтобы сохранить равновесие оставшейся в левой части массы жидкости, необходимо к ней приложить силу эквивалентную действию отброшенной части, которой очевидно является сила давления.

Предположим, что это сила 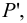которая имеет произвольное направление. Ее можно разложить на две составляющие: нормальную 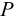и касательную к площадке Из-за текучести жидкости касательная составляющая 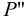привела бы жидкость в движение, т.е. в этом случае равновесие жидкости было бы невозможно, что не верно. Откуда следует вывод — сила давления всегда направлена по нормали.

Предположим, что это сила 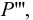которая стремится растянуть рассматриваемый объем жидкости. Но это невозможно, поскольку жидкость не сопротивляется растягивающим усилиям. Откуда следует вывод — сила давления может быть только сжимающей, т.е. действует по внутренней нормали к площадке действия.

Второе свойство состоит в том, что гидростатическое давление действует одинаково по всем направлениям, т.е. не зависит от ориентации площадки действия.

Докажем второе свойство. Для этого рассмотрим элементарно малый произвольный объём неподвижной жидкости в виде прямоугольного тетраэдра с ребрами 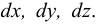Будем рассматривать этот объём в некоторой произвольной системе координат 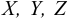(рис. 19).

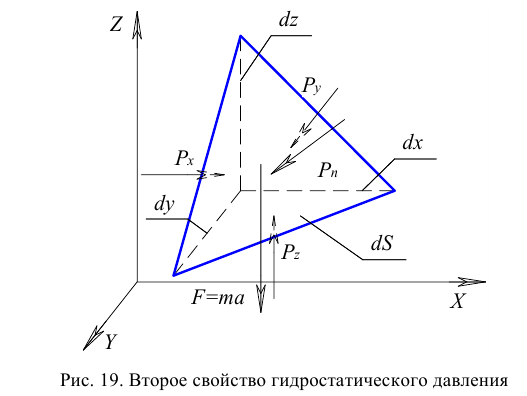
Тогда грани тетраэдра 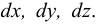лежат в координатных плоскостях, а четвертая грань площадью 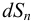наклонна и ориентирована нормально к направлению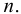

Отбросим окружающую тетраэдр жидкость и для сохранения равновесия объема приложим к каждой грани тетраэдра поверхностные силы давления

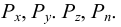
Кроме поверхностных сил на жидкость, заключенную в тетраэдре, действует массовая сила

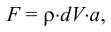
где 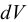— объем тетраэдра, ;

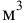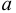— ускорение массовых сил, 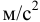. Записав в проекциях на координатные оси уравнения равновесия жидкости, заключенной в тетраэдре, получим

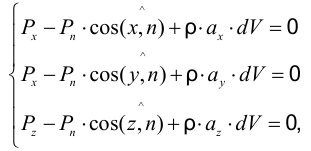
где обозначения

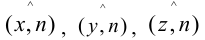
относятся к углам, образуемым нормалью к грани 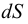с осями координат.

Так как объем тетраэдра равен

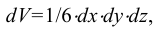
а площади граней

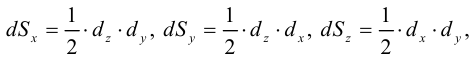
то можно записать

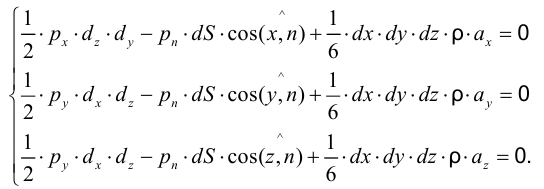
Разделив каждый член первого уравнения на 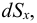второго — на 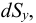третьего — на 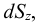получим

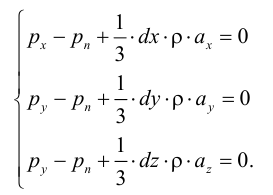
При стягивании рассматриваемого объема в точку, т.е. 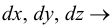0 и 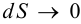, последняя система уравнений примет вид

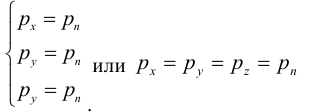
В результате можно сделать следующий вывод: давление не зависит от направления или другими словами: давление — величина скалярная.

Виды давления

Атмосферное давление — давление атмосферы на все находящиеся в ней предметы и земную поверхность. Оно создаётся гравитационным притяжением воздуха к Земле. Атмосферное давление измеряется барометром. Нормальным атмосферным давлением называют давление на уровне моря при температуре 15°С. Оно равно 760 мм рт. ст (миллиметров ртутного столба).

Рассмотрим два случая. Предположим, что давление в текучей среде соответствует положению точки 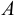, расположенной выше уровня атмосферного давления (рис. 20). Тогда абсолютное давление в этой точке 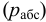отсчитывается от уровня абсолютного нуля давления (полного вакуума) до ее уровня. Превышение же давления над атмосферным называется избыточным или манометрическим давлением .

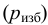Во втором случае, соответствующем положению точки 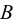(см. рис. 20), которая находится ниже уровня атмосферного давления абсолютное давление также рассчитывается от ноля но уровня точки. А недостаток давления до атмосферного называется вакуумом .

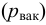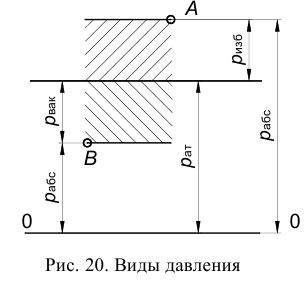
Кроме того, различают давление гидродинамическое и гидростатическое. Давление гидродинамическое возникает в движущейся жидкости. Гидростатическое давление -давление в покоящейся жидкости.

Единицей измерения давления в Международной системе единиц (СИ) является

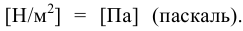
Паскаль — это очень маленькое давление, поэтому обычно пользуются укрупненными единицами измерения: килопаскалем

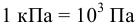
и мегапаскалем

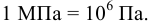
В давно изданной литературе можно встретить единицу измерения системы 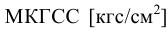, иначе именуемой технической атмосферой (ат.).

В технике часто пользуются несистемными единицами — бар, метры водного столба (м вод. ст.), миллиметры ртутного столба (мм рт. ст.), физическая атмосфера.

Связь этих единиц между собой следующая:

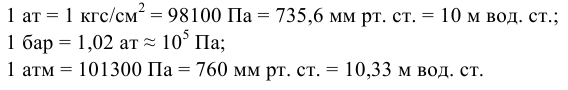
Поверхности равного давления

Поверхностью равного давления называется поверхность все точки которой испытывают одинаковое давление. Свободной поверхностью называют поверхность жидкости, которая граничит с газовой средой. Все точки такой поверхности испытывают одинаковое внешнее давление .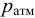

Поверхностями равного давления в объеме покоящейся относительно земли жидкости являются горизонтальные плоскости (рис. 21, а).

В случае покоя жидкости (рис. 21, б) относительно сосуда, который движется с ускорением 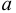, на частицы жидкости действуют силы тяжести 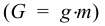и силы инерции 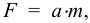направленные в сторону противоположную движению. Равнодействующая сил 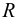не вертикальна, а лежит на нормали к поверхности равного давления. Свободная в этом случае поверхность представляет собой плоскость, наклоненную к горизонту под углом 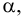т.е.

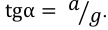
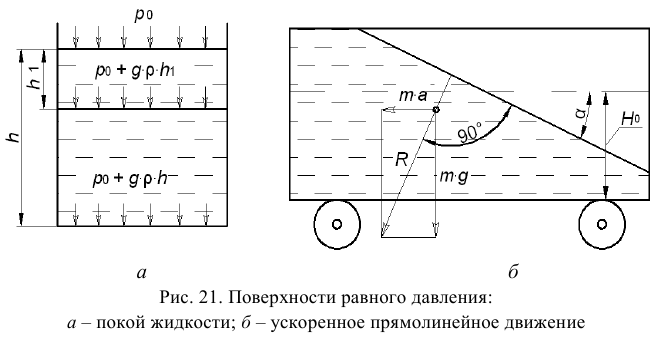
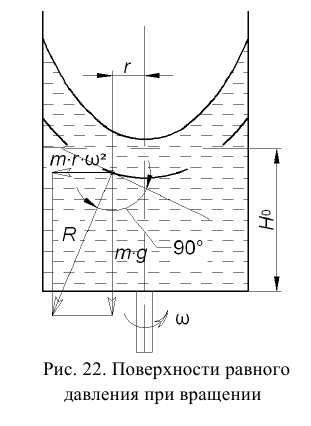
При относительном покое жидкости в сосуде (рис. 22), который вращается с угловой скоростью 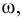на каждую частицу с координатой 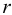действует сила тяжести 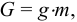и центробежная сила инерции 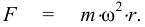. Равнодействующая сил 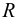лежит на нормали к касательной, проведенной через данную точку. Поверхность равного давления в этом случае представляет собой параболоид вращения.

Приборы для измерения давления

Существует два основных типа приборов для измерения давления в жидкости.

К приборам первого типа можно отнести жидкостные приборы пьезометры. Они представляют собой вертикальную трубку, обычно прозрачную, диаметром 10-И 5 мм. Если, например, нужно измерить давление в точке а, то достаточно подсоединить эту трубку к стенке сосуда так чтобы её конец находился на поверхности равного давления, проходящей через эту точку (рис. 23, а). В пьезометре установится уровень жидкости, пропорциональный давлению в точке А. Абсолютное давление в этой точке будет

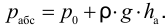
С другой стороны, это же давление можно представить как

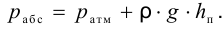
Отсюда

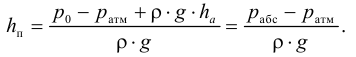
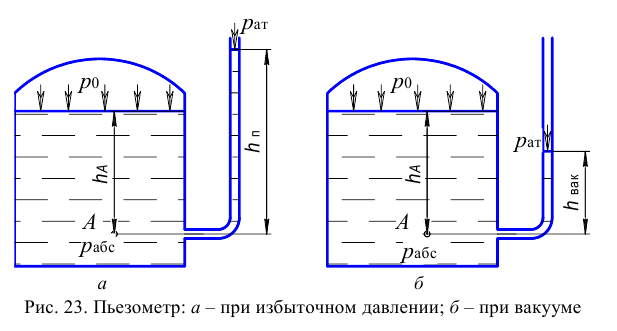
Величина 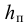называется пьезометрической высотой. По её величине судят о величине избыточного давления.

Если абсолютное давление меньше атмосферного 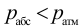, то в жидкости имеет место разрежение или вакуум (рис. 23, б). Такое давление называют вакуумметрическим давлением 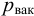, а высоту в пьезометре называют вакуумметрической высотой. Эти величины соответственно равны

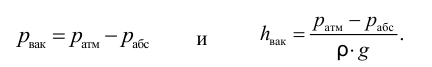
Ко второму типу приборов относятся манометры, которые имеют большое разнообразие по типам, размерам и характеристикам. Однако принципиально все эти приборы состоят из чувствительного элемента, который меняет свою форму (деформируется) под воздействием давления, и, связанного с этим элементом (рис. 23), передаточного механизма и регистрирующего прибора (индикатора).

Подсоединять манометры для измерения давления в определённой точке надо также как пьезометры, на уровне поверхности равного с выбранной точкой, давления.

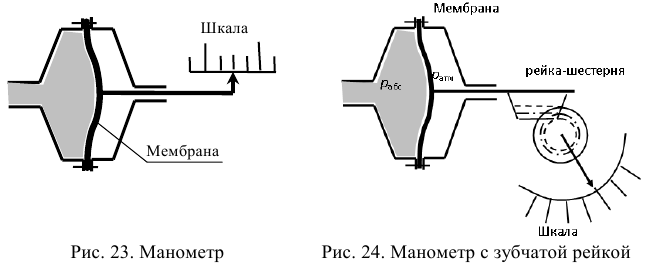
Под действием давления гибкий чувствительный элемент мембрана — изгибается. Размер этого отклонения пропорционален величине измеряемого давления. Вместе с мембраной отклоняется жёстко соединённая с ней стрелка, которая перемещается вдоль шкалы. Такой прибор отличается небольшим отклонением регистрирующего элемента — стрелки, следовательно, точность измерения большой быть не может.

Для увеличения чувствительности прибора мембрану можно соединить с зубчатой рейкой, находящейся в зацеплении с шестерней (рис. 24). Если с последней жёстко соединить стрелку, то при изменении давления она будет поворачиваться по отношению к круговой шкале. В этом случае изгиб мембраны даст большее, чем в первом случае, линейное отклонение конца стрелки. Это увеличит точность показаний прибора.

Общим недостатком таких приборов является малое исходное отклонение чувствительного элемента — мембраны.

Для устранения этого недостатка используются более сложные чувствительные элементы. Чаще всего таким элементом является полая трубка, согнутая по окружности (рис. 25). Один конец трубки связан со штуцером для подключения к измеряемому давлению, другой с зубчатым сектором, который связан с шестерней и стрелкой, поворачивающейся вокруг шкалы. При повышении давления трубка разгибается, и это отклонение значительно больше, чем отклонение мембраны при гаком же давлении. Во всех случаях чувствительный элемент (мембрану или гибкую трубку) можно связать с индуктивным электрическим преобразователем, состоящим из сердечника и электрической катушки. Можно также использовать пьезокристаллический преобразователь.

В обоих случаях будет генерироваться электрический сигнал, по величине пропорциональный силе давления. Этот сигнал после электрических аналоговых или же цифровых преобразователей можно передавать на очень большие расстояния и регистрировать цифровыми стрелочными индикаторами. Этот сигнал несложно также передавать для обработки компьютеру.

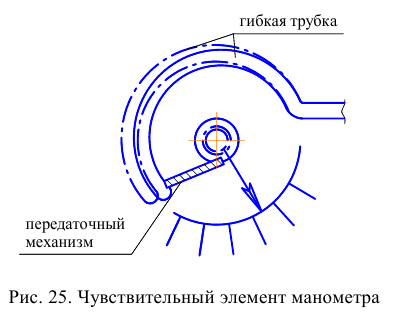
Дифференциальные уравнения равновесия покоящейся жидкости

Дифференциальные уравнения равновесия покоящейся жидкости иначе называют дифференциальными уравнениями Эйлера. Они получены для общего случая относительного покоя жидкости. Возможны следующие варианты относительного покоя.

Первый вариант соответствует абсолютному покою или равномерному движению сосуда с жидкостью. Такой вариант рассматривался при выводе основного уравнения гидростатики.

Второй вариант — вращение сосуда с жидкостью с постоянной угловой скоростью со вокруг центральной оси. Несмотря на то, что вся масса жидкости вращается вместе с сосудом, частицы жидкости друг относительно друга не перемещаются, следовательно, весь объём жидкости, как и в первом случае, представляет собой как бы твёрдое тело. Давление в каждой точке жидкости не меняется во времени и зависит только от координат. По этим причинам жидкость подпадает под определение покоящейся.

Третий вариант аналогичен второму, только вращение осуществляется вокруг произвольно расположенной вертикальной оси. Во втором и третьем случае свободная поверхность жидкости принимает новую форму, соответствующую новому равновесному положению жидкости.

В четвёртом варианте сосуд с жидкостью движется прямолинейно и равноускоренно. Такой случай проявляется, например, в процессе разгона или остановки автоцистерны с жидкостью. В этом случае жидкость занимает новое равновесное положение, свободная поверхность приобретает наклонное положение, которое сохраняется до изменения ускорения. Частицы жидкости друг относительно друга находятся в покое, и давление зависит только ог координат.

Во всех перечисленных случаях на жидкость действуют, во-первых, силы веса, во-вторых, силы инерции, в-третьих, силы давления.

Рассмотрим в произвольной системе координат 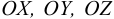(рис. 26) произвольную точку 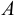. Вблизи этой точки выделим элементарный объём в форме прямоугольного параллелепипеда, грани которого (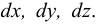) для простоты математических выражений параллельны координатным плоскостям.

Рассматриваемый объем, находится в равновесии под воздействием:

• поверхностных сил давления, направленных внутрь параллелепипеда нормально к его граням;
• объемных (массовых) сил, действующих на каждую частицу жидкости.

Рассмотрим действие сил давления. На площадку 1, которой принадлежит точка 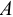, действует давление 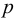, а направление этой составляющей силы давления совпадает с положительным направлением оси 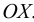. Грань 2 отстоит от грани 1 на расстоянии 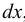, поэтому изменение давления в этом направлении составляет (направление этой составляющей силы давления противоположно-положительному направлению оси )

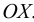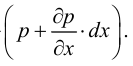
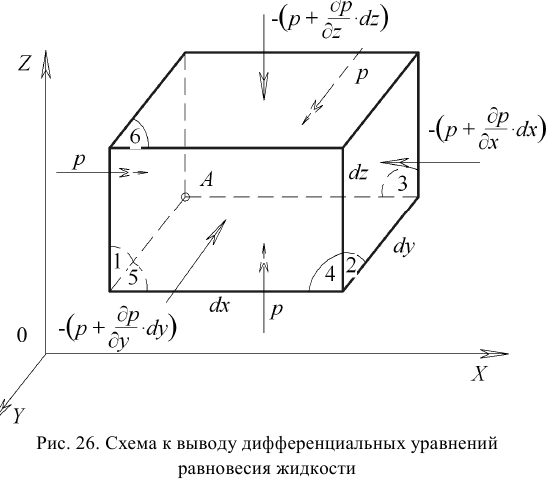
На площадку 3, которой принадлежит точка 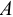, действует давление 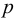, а направление этой составляющей силы давления совпадает с положительным направлением оси 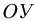. Грань 4 отстоит от грани 3 на расстоянии 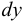, поэтому изменение давления в этом направлении составляет (направление этой составляющей силы давления противоположно положительному направлению оси )

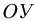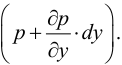
На площадку 5, которой принадлежит точка 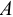, действует давление 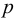, а направление этой составляющей силы давления совпадает с положительным направлением оси 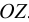. Грань 6 отстоит от грани 5 на расстоянии 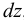, поэтому изменение давления в этом направлении составляет (направление этой составляющей силы давления противоположно положительному направлению оси )

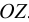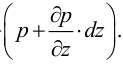
Тогда силы давления на соответствующие грани параллелепипеда выразятся как

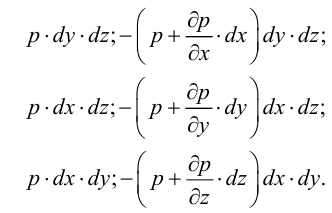
Массовую силу можно представить в виде

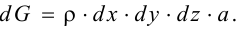
А проекции массовой силы 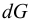на соответствующие оси будут иметь вид

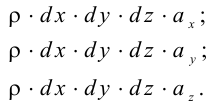
Для того, чтобы рассматриваемый объем находился в равновесии необходимо, чтобы сумма проекций всех сил, действующих на соответствующие грани была равна нулю. Или

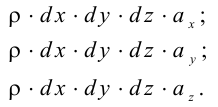
Исходя из этого, определим разности сил, вызванных давлением, в проекции на оси координат. Сократим каждый член первого уравнения на 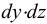, второго на — 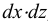, третьего на — 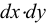и получим

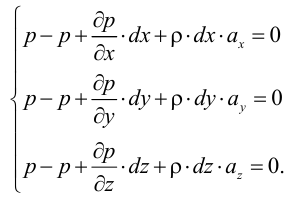
После соответствующих преобразований получим окончательно систему уравнений Эйлера

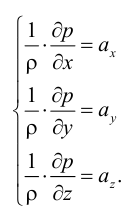
Возможно эта страница вам будет полезна:

Методические указания по гидравлике

Основное уравнение гидростатики

В системе уравнений Эйлера домножим каждый член первого уравнения на 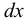, второго на — 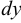, третьего на — 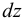и получим

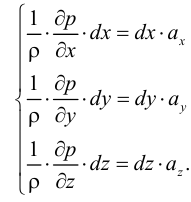
Проссумируем левые и правые части полученной системы

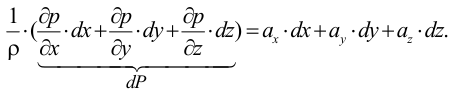
В последнем выражении сумма в скобках является полным дифференциалом давления, который в результате оказывается равным

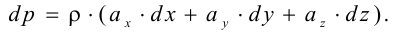
Рассмотрим простейший случай покоя жидкости (рис. 27). Из массовых сил на нее действует только сила тяжести. Это означает, что проекции ускорений этой силы на ос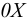и и 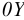отсутствуют, т.е.

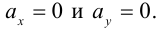
Единственным ускорением является ускорение свободного падения 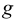, причем

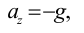
знак минус означает, что это ускорение направлено против положительного направления оси 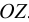. Тогда полный дифференциал давления после подстановки в него ускорений примет вид

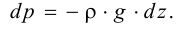
После интегрирования этого выражения получим

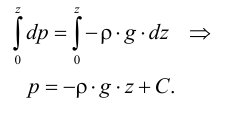
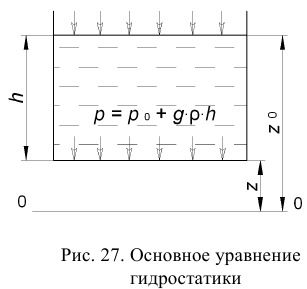
А поскольку сумма

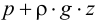
равна постоянной интегрирования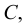

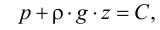
то можно записать

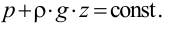
Последнее выражение называют основным уравнением гидростатики. Запишем его для частного случая (рис. 27), соответственно для свободной поверхности жидкости и дна бака

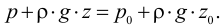
Выразим отсюда давление со стороны жидкости на дно бака

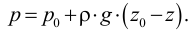
Но поскольку 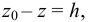окончательно получим

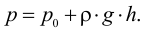
Откуда следует вывод, что давление зависит от глубины погружения точки под свободную поверхность с известным давлением на ней.

В последнем уравнении величина 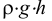выражает величину весового избыточного давления, создаваемого столбом жидкости высотой 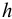. Иначе говоря, глубина погружения любой точки определяет избыточное давление в ней.

Физический смысл основного закона гидростатики

Пусть в открытом сосуде с жидкостью (рис. 28) на свободной поверхности внешнее давление 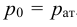. В точке 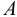, расположенной на глубине 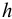под свободной поверхностью, полное гидростатическое давление определяется зависимостью 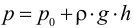а избыточное зависимостью

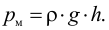
Присоединим к сосуду на уровне точки 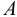тонкую стеклянную трубку с открытым концом. Жидкость поднимается по трубке. Поскольку на свободной поверхности в трубке давление также атмосферное, то жидкость остановится на уровне свободной поверхности в сосуде. Высота столба 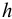жидкости в трубке зависит от манометрического давления 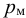, так как

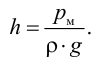
Высота

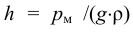
называется пьезометрической высотой, а трубка, с помощью которой можно измерить эту высоту, называется пьезометром.

Если к сосуду подсоединить трубку с запаянным концом (рис. 28) и откачать из нее воздух, т.е. создать в ней абсолютный вакуум 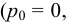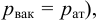то жидкость в этой трубке поднимется на большую высоту, величину которой можно установить путем следующих рассуждений.

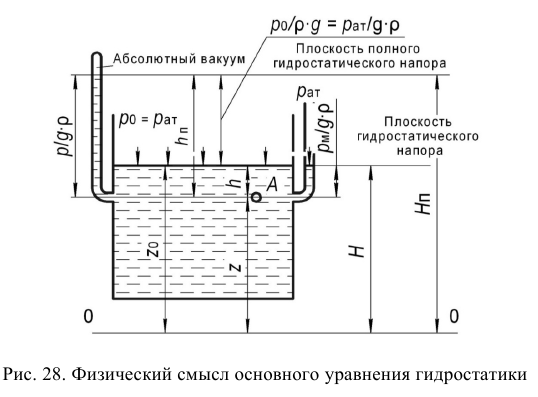
Из условия равновесия, обозначая высоту столба жидкости в запаянной трубке 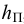, можно записать

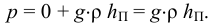
Следовательно, полное гидростатическое давление в точке соответствует высоте столба жидкости 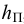, которая называется приведенной высотой. Разность уровней в открытом и запаянном пьезометрах соответствует атмосферному давлению или высоте столба воды 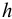= 10,33 м.

Итак, пьезометрическая высота соответствует величине манометрического давления, приведенная высота — величине полного гидростатического давления.

Если внешнее давление на свободной поверхности в сосуде больше атмосферного 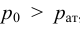, то в открытом пьезометре жидкость поднимется выше уровня в сосуде (рис. 29) на высоту столба жидкости, уравновешивающего разность давлений 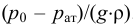. Следовательно, эта высота соответствует манометрическому давлению на свободной поверхности в сосуде, а пьезометрическая высота 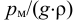манометрическому давлению в точке .

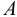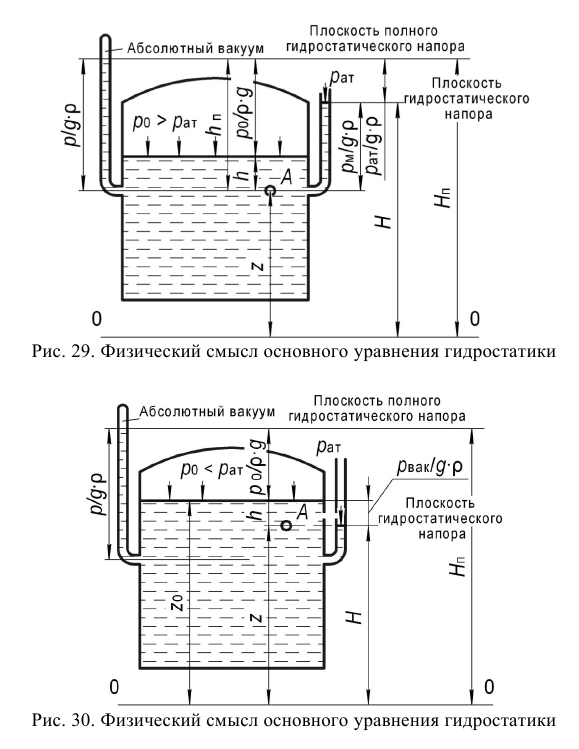
Если давление на свободной поверхности жидкости меньше атмосферного (вакуум), то в открытом пьезометре уровень установится ниже, чем в сосуде (рис. 30). Разность давлений на свободной поверхности в сосуде 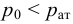и в трубке 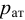уравновешивается столбом жидкости высотой 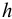. Ее значение соответствует вакууму на свободной поверхности. Действительно, если записать уравнение равновесия для любой точки в жидкости 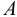, то давление со стороны сосуда определится как 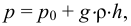, давление со стороны пьезометра как 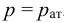. Отсюда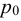

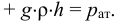
Проведем произвольную горизонтальную плоскость сравнения 0-0 и будем производить все вертикальные отсчеты от нее, считая положительным направление вверх.

Положение точки 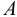определяется вертикальной координатой 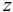. Величина 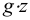выражает потенциальную энергию жидкости массой 1 кг, поднятой от плоскости 0-0 на высоту 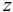. Кроме того, в рассматриваемой точке жидкость испытывает полное гидростатическое давление, под действием которого жидкость массой 1 кг может подняться еще на высоту 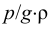. Т.е. полная потенциальная энергия, приходящаяся на единицу массы жидкости (полная удельная потенциальная энергия жидкости), складывается из двух величин: (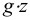) — удельной потенциальной энергии положения и 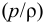— удельной потенциальной энергии давления. Если единица энергии Джоуль, то удельная энергия измеряется в Дж/кг.

Из основного уравнения гидростатики следует, что с физической точки зрения полная удельная потенциальная энергия для всех частиц жидкости, находящихся в покое, есть величина постоянная.

Разделив все члены уравнения

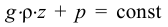
на произведение 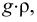получим выражение

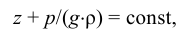
в котором каждый член имеет единицу измерения 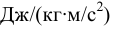= Дж/Н и представляет собой удельную энергию на 1Н силы веса протекающей жидкости. Но Дж/Н = Н-м/Н = м единица измерения напора.

В гидравлике принято использовать этот удобный вид уравнения, который позволяет дать геометрическую и энергетическую трактовку удельной энергии жидкости.

Величина

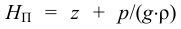
(см. рис. 29) называется полным гидростатическим напором. Все частицы в рассматриваемом объеме жидкости обладают одной и той же полной удельной потенциальной энергией 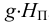. Горизонтальная плоскость, проведенная на уровне 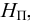называется плоскостью полного гидростатического напора.

Величина

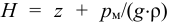
называется гидростатическим (или пьезометрическим) напором. Здесь

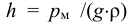
пьезометрическая высота. Пьезометрический напор отличается от полного гидростатического напора на высоту столба жидкости, соответствующую атмосферному давлению

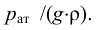
Горизонтальная плоскость, проведенная на уровне 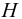ог плоскости сравнения, называется плоскостью гидростатического (или пьезометрического) напора. Для всех точек покоящейся жидкости пьезометрический напор постоянен (см. рис. 29).

Давление жидкости на окружающие её стенки

Важнейшей задачей гидростатики является определение сил, с которыми жидкость действует на окружающие её твёрдые стенки. Очень часто необходимо знать величину, направление и точку приложения сил, вызванных давлением, чтобы правильно провести прочностные расчёты элементов конструкции аппаратов и выбор арматуры. Проанализируем решение наиболее часто возникающих (типовых) задач.

Сила давления жидкости на плоское дно сосуда

Сила давления со стороны жидкости на плоское дно с площадью 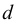(см. рис. 27)

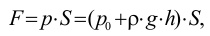
где 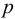— полное давление, Па.

Если внешнее давление 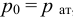, то сила давления равна

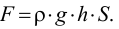
Таким образом, сила давления зависит от уровня жидкости в сосуде и площади дна. Для призматических емкостей произведение 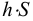представляет собой объем, заполненный жидкостью. Однако сила давления со стороны жидкости не зависит от объема.

Рассмотрим несколько сосудов различной формы, которые заполнены одной и той же жидкостью на одинаковый уровень 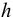и имеют одинаковую площадь дна, на свободную поверхность действует одинаковое давление (рис. 31). Для этих сосудов сила давления на дно

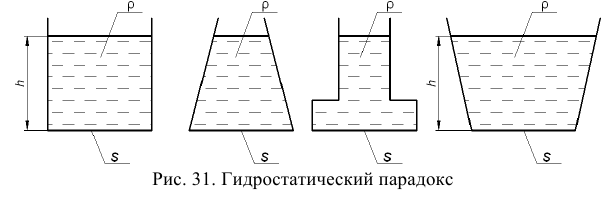
будет одинаковой, хотя сила веса жидкости в сосудах различная. Т.е. сила давления не зависит от объема, занимаемого жидкостью, а зависит только от площади дна и уровня жидкости в нем. В этом заключается так называемый гидростатический парадокс.

Сила давления жидкости на плоскую стенку

Рассмотрим стенку, наклоненную под углом 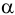к горизонту, (рис. 32) и определим силу давления со стороны жидкости, действующую на некоторый участок стенки, ограниченной контуром с площадью .

Выберем дополнительную систему координат, в которой ось 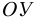направлена вдоль стенки, а начало координат лежит в точке пересечения свободной поверхности жидкости и проекции площадки, воспринимающей давление. Спроецируем рассматриваемую площадку на выбранную систему координат.

Элементарная сила давления, действующая на элементарно малую площадку площадью 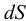, равна

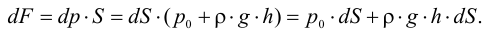
Для определения полной силы, действующей на всю площадку, проинтегрируем это выражение по площади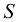

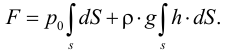
В последнем выражении

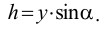
Подставив значение 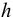в предыдущее выражение, будем иметь

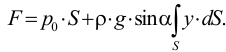
Из теоретической механики известно, что интеграл

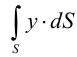
представляет собой статический момент площади относительно оси 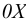. Он равен произведению этой площади на координату её центра тяжести, т.е. можно записать

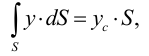
где 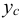— координата центра тяжести площадки, м.

Подставив статический момент площади в выражение силы, получим

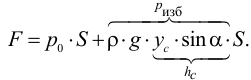
Выражение 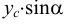— это глубина положения центра тяжести площадки, а 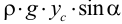— избыточное давление жидкости в центре тяжести площадки.

С учетом этого можно записать

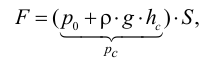
где 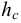— глубина погружения центра тяжести площадки, м.

Сумма в скобках в последнем выражении является абсолютным давлением в центре тяжести рассматриваемой площадки. Таким образом, можно сделать вывод: полная сила давления жидкости на плоскую стенку равна произведению её площади на величину гидростатического давления в центре тяжести этой площадки и направлена но внутренней нормали к площадке, воспринимающей давление.

Однако необходимо учесть, что эта сила не сконцентрирована в точке, а распределена но площади. И распределение это неравномерно, поскольку давление изменяется по гидростатическому закону, т.е. увеличивается с глубиной погружения. По этой причине для расчётов, кроме величины силы действующей на наклонную площадку, необходимо знать точку приложения равнодействующей. Для наклонной стенки центр тяжести не совпадает с этой точкой, называемой центром давления.

Центр давления — это точка пересечения равнодействующей сил давления со стороны жидкости с поверхностью, воспринимающей давление. Положение центра давления определяется двумя координатами. Но в гидротехнической практике используются сооружения симметричной формы. Поэтому обычно задача состоит в определении вертикальной координаты центра давления.

Координата центра давления yD определяется следующим образом

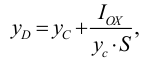
где 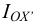— момент инерции площадки относительно оси 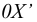параллельной оси 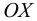и проходящей через центр тяжести площадки, .

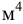Таким образом, разница в положениях центра тяжести площадки (т. 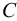) и центра давления (т. 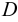) составляет

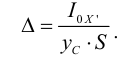
В итоге можно сделать следующие выводы. Если внешнее давление действует на стенку с обеих сторон, то найденная точка 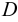(см. рис. 32) будет являться центром давления. Если внешнее давление со стороны жидкости выше давления с противоположной стороны (например, атмосферного), то центр давления находится по правилам механики как точка приложения равнодействующей двух сил: силы, создаваемой внешним давлением, и силы, создаваемой весом жидкости. При этом, чем больше внешнее давление, тем ближе располагается центр давления к центру тяжести.

Рассмотрим пример, когда жидкость воздействует на вертикальный щит прямоугольного сечения с размерами (рис. 33). Необходимо определить положение центра давления.

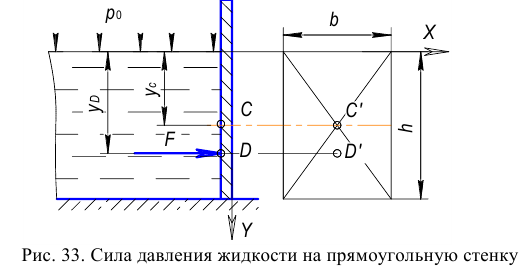
Координата центра тяжести площадки определится как

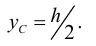
Момент инерции площадки прямоугольного сечения относительно оси 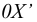параллельной оси 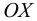и проходящей через центр тяжести площадки, будет равен

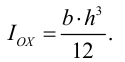
Площадь щига определится следующим образом

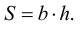
Координата центра давления рассматриваемой прямоугольной площадки будет равна

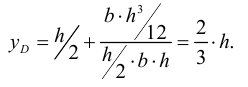
Сила давления жидкости на криволинейную стенку

Чаще всего необходимо определить силу, действующую на цилиндрическую поверхность, имеющую вертикальную ось симметрии. Возможны два варианта. Первый вариант — жидкость воздействует на стенку изнутри.

Во втором варианте жидкость действует на стенку снаружи. Рассмотрим оба этих варианта.

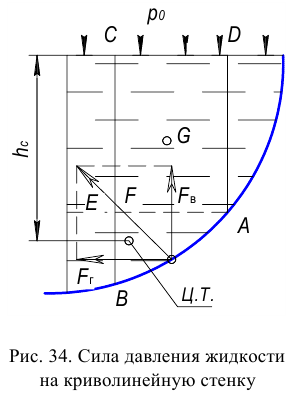
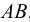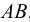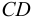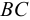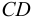В первом случае выделим объём жидкости, ограниченный рассматриваемым участком цилиндрической поверхности , участком свободной поверхности, расположенным, над участком , под и двумя вертикальными поверхностями и , проходящими через точки А и В. Эти поверхности ограничивают некоторый объём 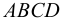, который находится в равновесии (рис. 34).

Рассмотрим равновесие этого объёма в вертикальном и горизонтальном направлениях.

Заметим, что, если жидкость действует на поверхность 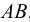, с какой-то силой 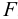, то с такой же силой, но в обратном направлении, и поверхность действует на рассматриваемый объём жидкости. Эту силу, перпендикулярную поверхности 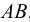, можно представить в виде горизонтальной 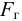и вертикальной 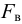составляющих.

Условие равновесия объёма 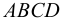в вертикальном направлении выглядит так

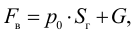
где 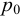— внешнее давление, Па;

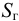— площадь горизонтальной проекции поверхности ;

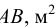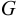— вес выделенного объёма жидкости, Н.

Условие равновесия этого объёма в горизонтальной плоскости запишем с учётом того, что силы, действующие на одинаковые вертикальные поверхност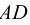и и 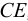, взаимно уравновешиваются. Остаётся только сила давления на площадь 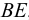, которая пропорциональна вертикальной проекции 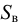поверхности 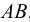. С учётом частичного уравновешивания будем иметь условие равновесия сил в горизонтальном направлении в виде

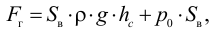
где 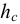— глубина расположения центра тяжести объема 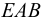, м.

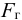Зная и 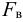, определим полную силу 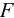, действующую на цилиндрическую поверхность:

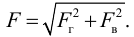
Во втором случае, когда жидкость воздействует на цилиндрическую поверхность снаружи, величина гидростатического давления во всех точках поверхности 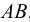имеет те же значения, что и в первом случае, так как определяется такой же глубиной. Силы, действующие на поверхность в горизонтальном и вертикальном направлениях, определяются по тем же формулам, но имеют противоположное направление. При этом под величиной 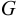надо понимать тот же объём жидкости 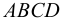, несмотря на то, что на самом деле он, в данном случае и не заполнен жидкостью.

Положение центра давления на цилиндрической стенке легко можно найти, если известны силы 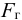и и 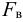определены центр давления на вертикальной проекции стенки и центр тяжести рассматриваемого объёма 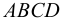. Задача упрощается, если рассматриваемая поверхность является круговой, так как равнодействующая сила при этом пересекает ось поверхности. Это происходит из-за того, что силы давления всегда перпендикулярны поверхности, а перпендикуляр к окружности всегда проходит через её центр.

Расчет тонкостенных цилиндрических сосудов, подверженных действию гидростатического давления

В гидравлических системах технологического назначения жидкость в основном передаётся по трубам круглого сечения. В водопроводах, канализационных и многих других трубопроводных системах, гидротехнических сооружениях широко используются трубы и различные резервуары круглого сечения. По этой причине задача определения нагрузки на трубу является весьма распространённой.

Проанализируем три наиболее распространенных случая.

• Рассмотрим трубу (рис. 35) длиной 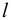с внутренним диаметром 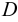и толщиной стенки 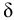, находящуюся под действием избыточного давления 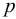. Это давление порождает разрывающее усилие 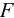, которое представляет собой силу давления, действующую на полуцилиндричекую поверхность, имеющую проекцию на любую из основных плоскостей площадью :

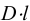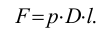
Из-за симметричности трубы такие разрывающие силы будут действовать одинаково во всех направлениях. Таким образом, стенки трубы работают на растяжение. Разрыву сопротивляется материал стенок площадью

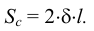
Напряжения растяжения, вызываемые давлением внутри грубы, можно определить как

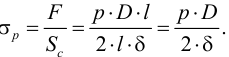
Условие прочности трубы

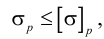
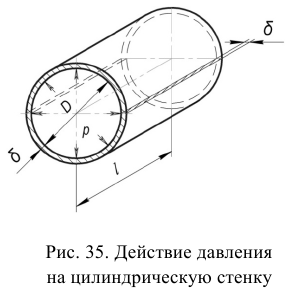
где 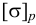— допускаемые напряжения растяжения для материала грубы, МПа.

Для случая проектного расчета, когда определяется толщина стенки сосуда, последнее выражение следует записать относительно толщины стенки и тогда получится

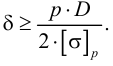
• Вертикальный сосуд заполнен жидкостью (сосуд под наливом). В этом случае (рис. 36) разрывающее сосуд усилие определяется как горизонтальная составляющая полного давления на полуцилиндрическую поверхность. В данном случае изменением давления по высоте обычно пренебрегают и ведут расчет по наибольшему давлению у дна сосуда

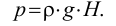
Растягивающее усилие в этом случае составляет величину

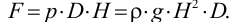
Площадь сопротивления составляет

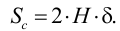
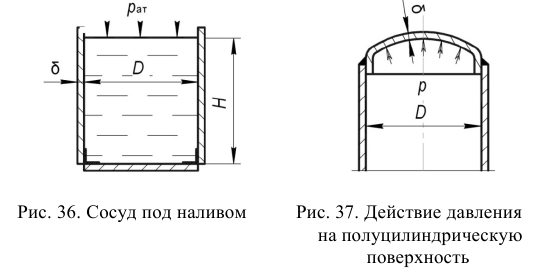
Напряжения растяжения соответственно равны

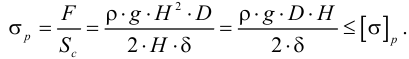
При проектном расчете по определению толщины стенки сосуда, работающего под наливом, получим

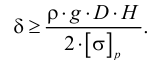
• А теперь определим толщину стенки сосуда из условия сопротивления разрыву, направленному вдоль оси сосуда (рис. 37)

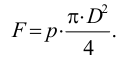
Сечение, в котором наиболее вероятен отрыв крышки от цилиндрической части сосуда

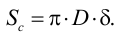
Напряжения растяжения соответственно равны

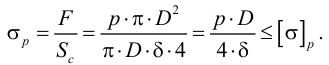
При проектном расчете но определению толщины стенки сосуда для данного случая будем иметь следующее соотношение

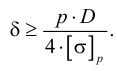
Таким образом, в последнем случае толщина стенки получается в два раза меньше, чем в первом случае. А поскольку наиболее опасной является вероятность разрыва сосуда в продольном направлении, то толщину стенки резервуара следует определять по выражениям, соответствующим первому рассмотренному случаю.

Зависимость же, полученную в третьем случае, используют для расчета на прочность сварных швов в месте крепления крышки и цилиндрической обечайки.

Основы теории плавания тел

Существование гидростатического давления приводит к тому, что на любое тело, находящееся в жидкости или газе, действует выталкивающая сила. Впервые значение этой силы в жидкостях определил на опыте Архимед.

Определим силу давления со стороны жидкости на погруженное в нее тело цилиндрической формы объемом 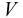(рис. 38). На верхнее основание площадью 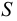действует сила гидростатического давления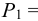 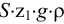, стремящаяся погрузить цилиндр в жидкость. На нижнее основание площадью 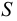действует сила гидростатического давления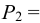 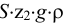, стремящаяся вытолкнуть тело из жидкости.

Горизонтальные составляющие сил давления взаимно уравновешиваются, так как они одинаковы по величине и противоположны по направлению. Таким образом, тело находится в равновесии.

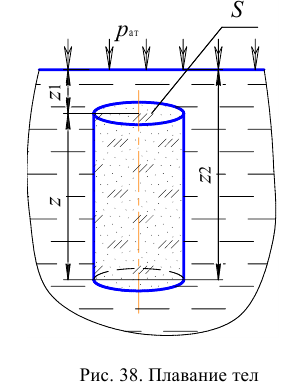
Равнодействующая сил давления, действующих на цилиндр, равна

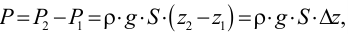
где 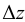— высота цилиндра, м.

Учитывая, что объем цилиндра равен 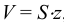, окончательно получим

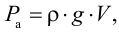
где 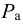— выталкивающая или архимедова сила, Н.

Таким образом, на тело, погруженное в жидкость, действует выталкивающая сила равная по величине и обратная по направлению весу вытесненной телом жидкости. Так формулируется закон Архимеда.

Плавучестью называется способность тела плавать при заданной нагрузке. Условие плавания в простейшем виде выглядит следующим образом

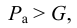
где — вес вытесненной жидкости, Н.

В зависимости ог отношения веса и выталкивающей силы возможны три состояния тела:

• если вес больше выталкивающей силы — тело тонет,
• если вес меньше выталкивающей силы — тело всплывает,
• если вес равен выталкивающей силе — тело плавает в погруженном состоянии.

Центром водоизмещения называется центр тяжести вытесненного телом объема жидкости (точка В, рис. 39). Иначе говоря, это точка приложения архимедовой силы.

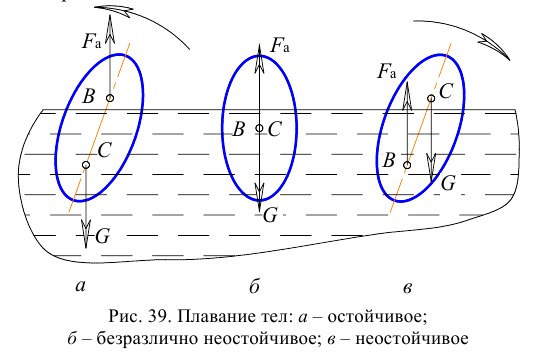
Остойчивостью называется способность тела при плавании возвращаться в положение равновесия после снятия нагрузки, вызвавшей нарушение равновесия.

В зависимости от взаимного расположения центра водоизмещения и центра тяжести плавающего тела (точка С) гак же возможны три состояния тела:

• если центр водоизмещения расположен выше центра тяжести плавание остойчиво и тело возвращается в положение равновесия (см. рис. 39, а),
• если центр водоизмещения совпадает с центром тяжести плавание безразлично неостойчиво (см. рис. 39, б),
• если центр водоизмещения расположен ниже центра тяжести -плавание неостойчиво (см. рис. 39, в).

Грузовой ватерлинией называется линия пересечения поверхности жидкости с боковой поверхностью плавающего объекта в нормальном положении (без крена) и при полной загрузке (линия 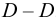, рис. 40).

Плоскость плавания — это площадка, ограниченная грузовой ватерлинией (площадка 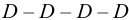, см. рис. 40).

Плавающее тело должно обладать запасом плавучести, то есть допустимой перегрузкой, при которой тело не тонет.

Плавающее тело может отклоняться от вертикального положения на некоторый угол крена 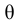(см. рис. 40).

Рассмотрим условия остойчивости. При крене тела центр водоизмещения катится по некоторой дуге радиусом 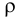из точки 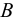в точку 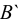а центр тяжести 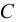не изменяет своего положения (см. рис. 40, а). Точка 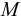пересечения линии действия выталкивающей силы 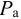с осью плавания тела 0-0 называется метацентром. Расстояние от центра водоизмещения до метацентра называется метацентрическим радиусом 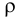. Мегацентрической высотой 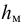называется расстояние между центром тяжести тела и метацентром.

Если положение метацентра выше положения центра тяжести тела 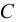, т.е. мегацентрический радиус 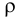больше эксцентриситета 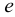(расстояния между центром водоизмещения и центром тяжести), то плавание будет остойчивым, а мегацентрическая высота 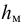положительной (см. рис. 40, а). Это объясняется тем, что возникающий при крене момент сил, действующих на тело, будет стремиться вернуть тело в положение равновесия после снятия отклоняющей нагрузки. Условие остойчивого плавания можно представить в следующем виде

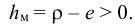
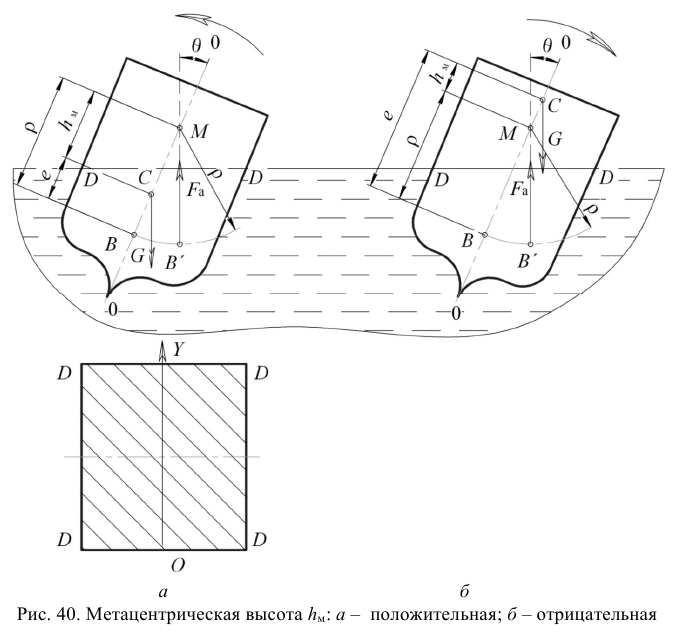
Таким образом, если метацентрическая высота положительна, то остойчивость тела при плавании обеспечена.

Если положение метацентра ниже центра тяжести плавающего тела, то метацентрическая высота 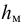отрицательна, следовательно, возникающая пара сил стремится опрокинуть тело, и плавание будет неостойчивым (см. рис. 40, 6). При этом возникает условие

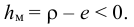
Метацентрический радиус определяется но формуле

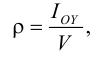
где 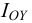— момент инерции площади относительно продольной оси 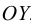, проходящей через центр тяжести этой площадки, ;

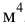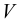— объем, погруженный в жидкость, .

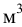Условие остойчивого плавания иначе можно представить в следующем виде

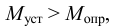
где 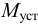— момент устойчивости, Нм;

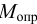— опрокидывающий момент, Н м.

Момент устойчивости можно найти так

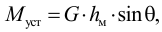
где 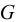— вес вытесненного объема жидкости, Н;

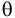— угол крена.

Если твердое тело однородно, т. е. во всех точках имеет одну и ту же плотность, то тело будет тонуть, всплывать или оставаться в равновесии внутри жидкости в зависимости от того, больше ли плотность тела плотности жидкости, меньше или равна ей. В случае неоднородных тел нужно сравнивать с плотностью жидкости среднюю плотность тела. Плавающие тела разных плотностей погружаются в жидкость на разную долю своего объема. Это объясняется тем, что при равновесии тела, плавающего на поверхности жидкости, вес вытесненного объема жидкости (в данном случае — объема части тела, находящейся под свободным уровнем жидкости) должен быть равен весу тела. Поэтому тело, плотность которого лишь незначительно меньше плотности жидкости (например, льдина в воде), погружается при плавании глубоко.

Тело, имеющее полости, куда жидкость не проникает при плавании тела, вытесняет такой же объем, что и сплошное тело. Поэтому и выталкивающая сила для такого тела та же, что и для сплошного. Но масса тела с полостями меньше массы сплошного тела; поэтому при достаточно больших полостях такое тело может плавать даже в том случае, когда плотность вещества тела больше плотности жидкости. Вытесненный объем оказывается больше объема, занятого веществом тела.

Железный корабль вытесняет объем воды во много раз больший, чем объем железа, из которого сделан корпус судна; поэтому он может плавать (имеет «плавучесть»), несмотря на то, что плотность железа в 7,8 раза больше плотности воды. Если пространство внутри судна заполнится водой, например, в случае течи, то вытесненный объем уменьшится, судно потеряет плавучесть и начнет тонуть. Для обеспечения безопасности мореплавания следует предусматривать возможность пробоины в корпусе судна. Все внутреннее пространство разделяют рядом стальных переборок на водонепроницаемые отделения «отсеки». В случае пробоины или течи заполняется водой только один из отсеков, и судно продолжает плавать, хотя и погружается несколько глубже в воду.

Особый вид кораблей представляют собой подводные лодки. Они должны иметь возможность всплывать и погружаться в воду, а также плыть под поверхностью воды. Так как объем лодки остается во всех случаях неизменным, то для выполнения этих маневров на лодке должно быть устройство для изменения ее массы. Это устройство состоит из ряда балластных отсеков в корпусе лодки, которые при помощи специальных устройств можно заполнять забортной водой (при этом масса лодки увеличивается и она погружается) или освобождать от воды (при этом масса лодки уменьшается и она всплывает).

Заметим, что достаточно небольшого избытка или недостатка воды в балластных отсеках, чтобы лодка ушла на самое дно моря или всплыла на поверхность воды. Часто бывает, что в некотором слое плотность воды быстро меняется по глубине, возрастая сверху вниз. Вблизи уровня такого слоя равновесие лодки устойчиво. Действительно, если лодка, находясь на таком уровне, по какой-либо причине погрузится немного глубже, то она попадет в область большей плотности воды. Выталкивающая сила увеличится, и лодка начнет всплывать, возвращаясь к первоначальной глубине. Если же лодка по какой-либо причине поднимется вверх, то она попадает в область меньшей плотности воды, выталкивающая сила уменьшится, и лодка снова вернется к первоначальному уровню. Поэтому подводники называют такие слои «жидким грунтом»: лодка может «лежать» на нем, сохраняя равновесие неопределенно долгое время, в то время как в однородной среде это не удается и для сохранения заданной глубины лодка либо должна все время изменять количество балласта, принимая или вытесняя воду из балластных отсеков, либо должна все время двигаться, маневрируя рулями глубины.

Кинематика жидкости

Основной задачей этого раздела гидравлики является определение зависимостей скорости 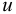и давления 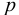в каждой точке потока жидкости, которые являются соответствующими функциями времени 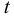и координат :

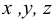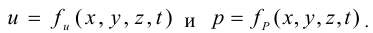
Изучение этих зависимостей начнём с рассмотрения идеальной жидкости, иод которой будем понимать воображаемую жидкость, не имеющую вязкости и, следовательно, не имеющую сил внутреннего трения. Давление в такой жидкости имеет свойства статического давления, т.е. направлено по внутренней нормали и передаётся одинаково во всех направлениях.

Виды движения (течения) жидкости

Течение жидкости вообще может быть неустановившимся (нестационарным) или установившимся (стационарным).

Неустановившееся движение — такое, при котором в любой точке потока скорость движения и давление с течением времени изменяются, т.е. 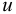и 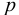зависят не только от координат точки в потоке, но и от момента времени, в который определяются характеристики движения

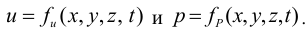
Примером неустановившегося движения может являться истечение жидкости из опорожняющегося сосуда, при котором уровень жидкости в сосуде постепенно меняется (уменьшается) по мере истечения из него жидкости.

Установившееся движение — такое, при котором в любой точке потока скорость движения и давление с течением времени не изменяются, т.е. 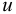и 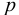зависят только от координат точки в потоке, но не зависят от момента времени, в который определяются характеристики движения

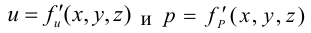
и, следовательно,

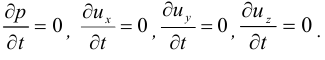
Пример установившегося движения — истечение жидкости из сосуда с постоянным уровнем, который не меняется (остаётся постоянным) по мере истечения жидкости.

В случае установившегося течения в процессе движения любая частица, попадая в заданное относительно твёрдых стенок, место потока, всегда имеет одинаковые параметры движения. Следовательно, каждая частица движется по определённой траектории.

Траекторией называется путь, проходимый данной частицей жидкости в пространстве за определенный промежуток времени.

При установившемся движении форма траекторий не изменяется во время движения. В случае неустановившегося движения величины направления и скорости движения любой частицы жидкости непрерывно изменяются, следовательно, и траектории движения частиц в этом случае также постоянно изменяются во времени.

Поэтому для рассмотрения картины движения, образующейся в каждый момент времени, применяется понятие линии тока.

Линия тока — это кривая, проведенная в движущейся жидкости в данный момент времени так, что в каждой точке векторы скорости 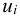совпадают с касательными к этой кривой (рис. 41).

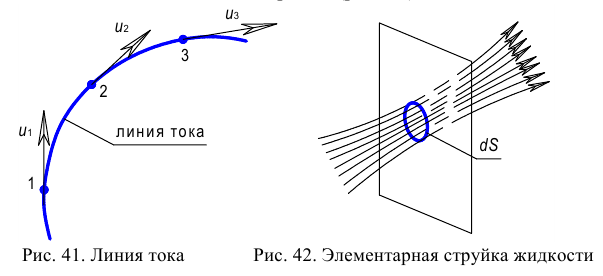
Нужно различать траекторию и линию тока. Траектория характеризует путь, проходимый одной определенной частицей, а линия тока направление движения в данный момент времени каждой частицы жидкости, лежащей на ней.

При установившемся движении линии тока совпадают с траекториями частиц жидкости. При неустановившемся движении они не совпадают, и каждая частица жидкости лишь один момент времени находится на линии тока, которая сама существует лишь в это мгновение. В следующий момент возникают другие линии тока, на которых будут располагаться другие частицы. Еще через мгновение картина опять меняется.

Если выделить в движущейся жидкости элементарный замкнутый контур площадью 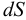и через все точки этого контура провести линии тока, то получится трубчатая поверхность, которую называют трубкой тока. Часть потока, ограниченная поверхностью трубки тока, называется элементарной струйкой жидкости (рис. 42). Таким образом, элементарная струйка жидкости заполняет трубку тока и ограничена линиями тока, проходящими через точки выделенного контура с площадью 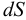. Если 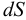устремить к 0, то элементарная струйка превратится в линию тока.

Из приведённых выше определений вытекает, что в любом месте поверхности каждой элементарной струйки (трубки тока) в любой момент времени вектора скоростей направлены по касательной (и, следовательно, нормальные составляющие отсутствуют). Это означает, что ни одна частица жидкости не может проникнуть внутрь струйки или выйти наружу.

При установившемся движении элементарная струйка жидкости обладает рядом свойств:

• площадь поперечного сечения струйки и ее форма с течением времени не изменяются, гак как не изменяются линии тока;
• отсутствует приток или отток частиц жидкости через боковую поверхность элементарной струйки, т.е. поверхность струйки как бы непроницаема;
• во всех точках поперечного сечения элементарной струйки скорости движения одинаковы вследствие малой площади поперечного сечения;
• форма и площадь поперечного сечения элементарной струйки и скорости в различных поперечных сечениях струйки могут изменяться.

При неустановившемся движении форма и местоположение элементарных струек непрерывно изменяются.

Кроме того установившееся движение подразделяется на равномерное и неравномерное.

Равномерное движение характеризуется тем, что скорости, форма и площадь сечения потока не изменяются по длине потока. Простейший случай такого движения — это движение жидкости по трубе цилиндрической формы.

Неравномерное движение отличается изменением скоростей, глубин, площадей сечений потока но длине потока. Простейший случай такого движения — это движение жидкости по трубе конической формы.

Среди неравномерно движущихся потоков следует отметить плавно изменяющееся движение, характеризующееся тем, что:

• линии тока искривляются мало;
• линии тока почти параллельны, и живое сечение можно считать

плоским;

• давления в живом сечении потока зависят ог глубины.

Движение потоков жидкости можно также подразделить на напорное и безнапорное.

Безнапорное движение жидкости отличается тем, что поток имеет свободную поверхность, граничащую с газовой средой. Безнапорное движение происходит под действием исключительно сил тяжести самого потока жидкости (рис. 43, а). Давление в таких потоках примерно одинаково и отличается от атмосферного только за счет глубины потока. Примером такого движения может быть течение воды в реке, канале, ручье.

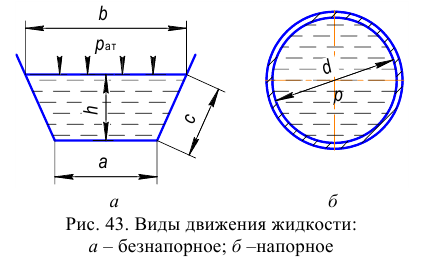
Напорное движение жидкости — это такое движение, когда поток со всех сторон ограничен твердыми стенками (рис. 43, б), при этом в любой точке потока давление отличается от атмосферного обычно в большую сторону, но может быть и меньше атмосферного. Движение в этом случае происходит за счёт давления, создаваемого, например, насосом или водонапорной башней. Такое движение имеет место во всех трубопроводах технологического оборудования, водопроводах, отопительных системах и т.п.

Кроме напорного и безнапорного движений можно отдельно выделить существование свободных струй, которые не ограничены твёрдыми стенками. Движение происходит иод действием сил инерции и веса жидкости. Давление в гаком потоке практически равно атмосферному. Пример свободной струи — истечение жидкости из сопла, форсунки и т.п.

В гидравлике рассматривается струйная модель движения жидкости, т.е. ноток представляется как совокупность элементарных струек жидкости, имеющих различные скорости течения скц. Индекс «/» означает, что в каждой точке живого сечения скорости различны. Элементарные струйки как бы скользят друг по другу. Они трутся между собой и вследствие этого их скорости различаются. Причём, в середине потока скорости наибольшие, а к периферии они уменьшаются. А поток — это масса движущейся жидкости, ограниченная твердыми стенками.

Гидравлические характеристики потока жидкости

В гидравлике различают следующие характеристики потока: живое сечение, смоченный периметр, гидравлический радиус, расход, средняя скорость.

Живым сечением потока называется поверхность (поперечное сечение), нормальная ко всем линиям тока, его пересекающим, и лежащая внутри потока жидкости. Для элементарной струйки жидкости используют понятие живого сечения элементарной струйки (сечение струйки, перпендикулярное линиям тока), площадь которого обозначают через .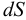

Смоченный периметр потока 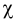— линия, по которой жидкость соприкасается с поверхностями русла в данном живом сечении. В безнапорных потоках смоченный периметр не совпадает с геометрическим периметром (см. рис. 43, а). А в напорных потоках смоченный периметр совпадает с геометрическим периметром, так как поток жидкости соприкасается со всеми твёрдыми стенками (см. рис. 43, б).

Гидравлическим радиусом 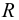потока называется часто используемая в гидравлике величина, представляющая собой отношение площади живого сечения 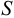к смоченному периметру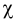

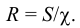
При безнапорном движении (см. рис. 43, а) гидравлический радиус будет равен

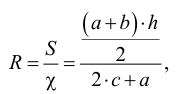
где — размеры поперечного сечения русла, м.

Свободная поверхность жидкости при определении смоченного периметра не учитывается.

При напорном движении в трубе круглого сечения (см. рис. 43, 6) гидравлический радиус будет равен

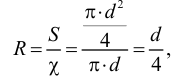
т.е. четверти диаметра 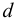или половине радиуса трубы.

Расход потока жидкости (расход жидкости) — количество жидкости, протекающей в единицу времени через живое сечение потока.

Различают объёмный, массовый и весовой расходы жидкости. Объёмный расход жидкости — это объём жидкости, протекающей в единицу времени через живое сечение потока

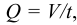
где 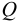— объёмный расход жидкости, ;

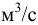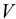— объём жидкости, протекающий через живое сечение потока, 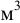; 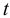— время течения жидкости, с. Массовый расход жидкости — это масса жидкости, протекающей в единицу времени через живое сечение потока

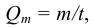
где 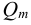— массовый расход жидкости, кг/с;

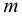— масса жидкости, протекающий через живое сечение потока, кг. Весовой расход жидкости — это вес жидкости, протекающей в единицу времени через живое сечение потока

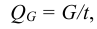
где 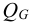— весовой расход жидкости Н/с;

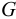— вес жидкости, протекающий через живое сечение потока, Н.

Связь между объемным расходом и массовым следующая

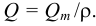
Чаще всего используется объёмный расход потока жидкости. С учётом того, что поток складывается из элементарных струек, то и расход потока складывается из расходов элементарных струек жидкости .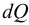

Расход элементарной струйки — объем жидкости 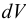, проходящей через живое сечение струйки в единицу времени. Таким образом

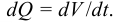
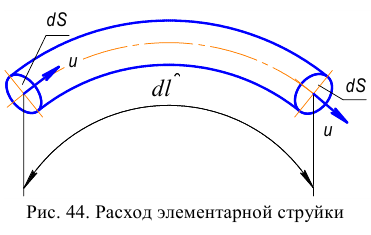
Рассмотрим отсек элементарный струйки постоянного сечения (рис. 44) длиной 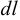и площадью 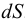. Объем этого отсека равен 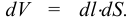. Тогда расход струйки

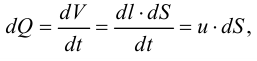
где 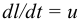— скорость, м/с.

Поскольку расход потока это сумма расходов элементарных струек, составляющих его, то выражение для расхода элементарной струйки необходимо проинтегрировать по площади живого сечения потока. Тогда получается выражение для объёмного расхода жидкости как суммы расходов элементарных струек

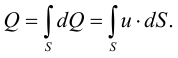
Применение этой зависимости в расчетах весьма затруднительно, гак как расходы элементарных струек жидкости в различных точках живого сечения потока различны. Кроме того, характер распределения скоростей по живому сечению потока обычно неизвестен. Поэтому в практике для определения расхода чаще пользуются понятием средней скорости потока.

Средняя скорость потока жидкости 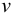— это фиктивная скорость потока одинаковая для всех точек данного живого сечения потока, но при которой расход равняется фактическому

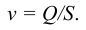
Тогда расход потока можно представить как произведение средней скорости на площадь живого сечения потока

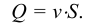
При неравномерном движении средняя скорость в различных живых сечениях по длине потока различна. При равномерном движении средняя скорость по длине потока постоянна во всех живых сечениях.

Уравнение неразрывности для элементарной струйки жидкости

В технологическом оборудовании чаще всего рассматривают потоки, в которых не образуются разрывы жидкости, т.е. жидкость сплошь заполняет пространство.

Рассмотрим элементарную струйку несжимаемой жидкости при установившемся движении, в которой выделим три произвольных сечения 7-7, 2-2 и 3-3, расположенные на некотором расстоянии одно от другого с площадями сечений

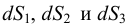
соответственно (рис. 45). Очевидно, что расходы элементарной струйки в соответствующих живых сечениях будут равны

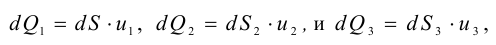
причём расход 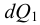втекает в рассматриваемый участок элементарной струйки, a 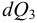— вытекает из него.

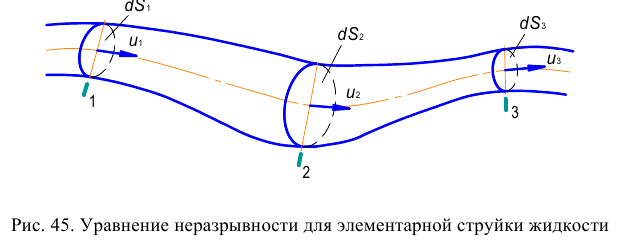
Учтём, что форма элементарной струйки не изменяется с течением времени, а поперечный приток и отток невозможны, так как скорости на боковой поверхности струйки направлены по касательным к линиям тока, из которых состоит эта боковая поверхность, тогда получаем, что расходы 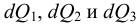равны, т.е.

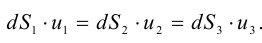
Вследствие того, что сечения 1-1, 2-2 и 3-3 выбраны произвольно, подобные соотношения справедливы для любых сечений элементарной струйки. Следовательно, можно записать

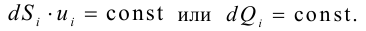
Последнее соотношение называется уравнением неразрывности в гидравлической форме для элементарной струйки несжимаемой жидкости при установившемся движении. Сформулировать его можно так: расход, проходящий через все поперечные сечения элементарной струйки, постоянен по длине.

Уравнение неразрывности для потока жидкости при установившемся движении

Поскольку расход потока состоит их суммы расходов элементарных струек, то можно просуммировать расходы всех элементарных струек в каждом живом сечении потока. В результате получится уравнение неразрывности для потока при установившемся движении. Обычно его записывают в одном из следующих видов

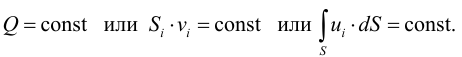
Таким образом, расход, проходящий через все поперечные сечения потока, постоянен по длине. Уравнение неразрывности является частным случаем закона сохранения массы.

Для несжимаемой жидкости при установившемся движении жидкости расход во всех живых сечениях потока одинаков, несмотря на то, что площади живого сечения и средние скорости в каждом сечении и могут быть разными.

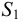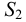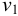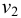Рассмотрим поток жидкости, имеющий два сечения с площадями поперечных сечений и и средними скоростями в них и соответственно (рис. 46).

Тогда уравнение неразрывности для этих сечений можно записать в следующем виде

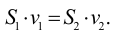
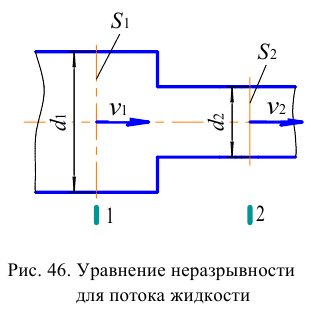
Поскольку площадь поперечного сечения круглой трубы

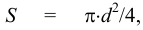
получим следующее важное соотношение

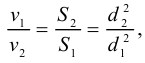
т.е. отношение средних скоростей в живых сечениях потока обратно пропорционально отношению их площадей или обратно пропорционально отношению квадратов диаметров.

Динамика жидкостей

Главная задача данного раздела, вместе с разделом кинематики жидкостей, заключается в установлении связей между силами, действующими в потоке жидкости и характеристиками движения этой жидкости. Эти связи в общем случае представляются уравнениями вида

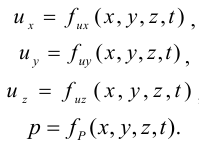
Нахождение этих функций является весьма сложной задачей. Поэтому для упрощения её решения Леонард Эйлер предположил, что жидкость является идеальной, т.е. не имеющей вязкости, а также то, что все перечисленные функции непрерывные и дифференцируемые, хотя физической причиной непрерывности распределения скоростей в движущейся жидкости является именно вязкость.

Дифференциальные уравнения Эйлера движения идеальной жидкости

Для вывода дифференциальных уравнений движения жидкости используем полученные ранее дифференциальные уравнения равновесия покоящейся жидкости в виде

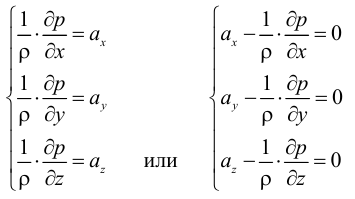
Напомним, что левые части уравнений первой системы характеризуют действие поверхностных сил давления, а правые действие массовых сил. Для того, чтобы получить уравнения движения можно воспользоваться принципом Д’Аламбера, т.е. для перехода от равновесия к движению необходимо к действующим силам прибавить силы инерции, возникающие при движении жидкости.

При движении жидкости частицы приобретают скорость, которую можно представить в следующем виде

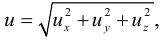
где 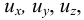, — проекции вектора скорости и на соответствующие основные оси выбранной системы координат, м/с.

Ускорение же сил инерции, возникающих при движении жидкости, можно представить как

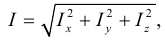
где 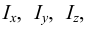— проекции вектора ускорения 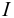на соответствующие основные оси выбранной системы координат, 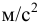. В свою очередь составляющие вектора ускорения можно выразить через составляющие скорости в следующем виде

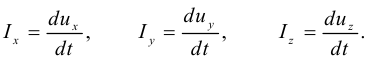
Прибавляя силы инерции к действующим силам и помещая их в правую часть уравнений, получим

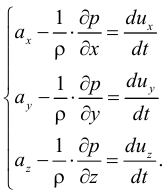
Эти уравнения были получены в 1755 г. академиком Российской Академии наук Леонардом Эйлером и называются дифференциальными уравнениями движения невязкой жидкости. Эти уравнения справедливы для идеальной жидкости, т.е. для движения без внутреннего сопротивления (вязкости), и они описывают связь между силами, действующими в жидкости и законами её движения.

Дифференциалы скоростей

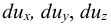
представим в виде частных производных так

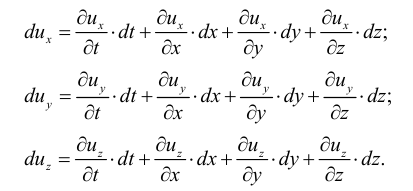
Тогда полные производные

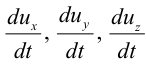
можно представить следующим образом

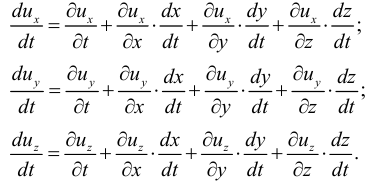
В правой части выражений для полных производных составляющих скорости выполним преобразования, поскольку

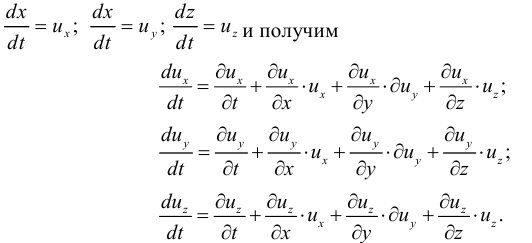
Подставим полученные выражения полных производных составляющих скорости в дифференциальные уравнения движения невязкой жидкости

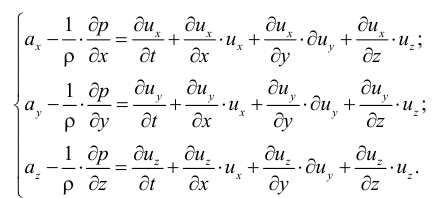
Уравнения — это уравнения Эйлера для движения невязкой жидкости, записанные в развернутом виде. Первые составляющие левой части выражают силы гидродинамического давления, вторые — внешние действующие силы, а в правой части представлены силы инерции.

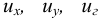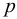Полученные в таком виде дифференциальные уравнения Эйлера положили начало практическому изучению движения жидкости. Поскольку для нахождения четырех неизвестных и недостаточно трех уравнений, то к ним прибавляют четвертое -уравнение неразрывности или сплошности движения для несжимаемой жидкости.

В правые части уравнений входят девять частных производных проекций скорости по координатам 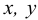и 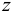. Три из этих производных 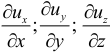называются прямыми или продольными. Каждая из них взята по координате, отмеряемой по той оси, на которую проецируется скорость.

Остальные шесть частных производных называются косыми или поперечными. Каждая из них берется по координате, отмеряемой поперек оси, на которую проецируется скорость. Например, члены

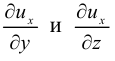
показывают, как изменяется значение скорости в направлении 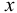(в проекции на ось 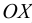) в зависимости от изменения координат на перпендикулярных осях 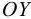и .

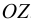Слагаемые

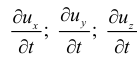
описывают изменение скорости жидкости во времени, т.е. характеризуют неустановившийся режим течения жидкости. Если течение установившееся, то эти слагаемые равны нулю.

Преобразование уравнений Эйлера

Так же как и в статике, чтобы избавиться от частных производных, умножим каждый член первого уравнения системы дифференциальных уравнений движения невязкой жидкости на 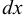, второго на — 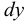и третьего на — 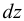соответственно и проссумируем левые и правые части

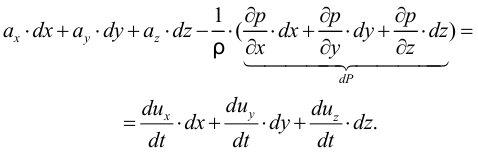
Проанализируем полученное уравнение.

Первые три слагаемые

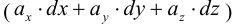
По существу являются суммой инерционных сил или веса, действующих в жидкости. Обозначим эту сумму 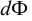и назовём её силовой функцией или точнее силовой потенциальной функцией.

Вспомним из статики, что

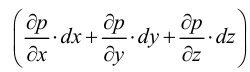
есть полный дифференциал давления .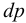

Учтём также, что каждое слагаемое в правой части можно переписать в другом виде. Например,

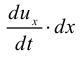
представить как

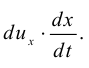
В свою очередь

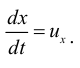
И тогда окончательно

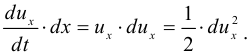
Применив такие же преобразования ко всем трём слагаемым, получим

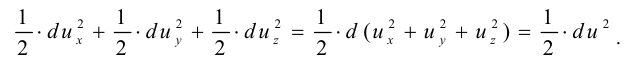
С учётом проведённого анализа преобразуем «сложенные уравнения» к обобщённой форме уравнений Эйлера

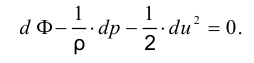
Возможно эта страница вам будет полезна:

Примеры решения задач по гидравлике

Интегрирование уравнений Эйлера

Интегрирование уравнений Эйлера рассмотрим на широко распространённом примере движения жидкости под действием силы тяжести. Примерами такого движения могут служить: течение реки, ручья или любого другого потока жидкости, течение жидкости в водопроводе, работающем от водонапорной башни.

Движение жидкости описывается обобщённой формой уравнений Эйлера

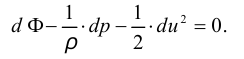
В рассматриваемом случае, когда движение жидкости осуществляется исключительно под действием силы тяжести, силовая потенциальная функция

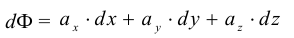
принимает вид

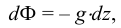
где 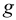— ускорение свободного падения, .

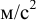Подставив это выражение в уравнение Эйлера, и умножив на «-1», для того чтобы избавиться ог знаков «минус», получим

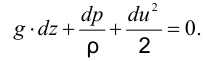
После интегрирования придём к следующему виду

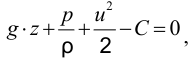
где 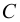— постоянная интегрирования (знак «-» перед ней не имеет физического значения и поставлен только для удобства последующих математических преобразований).

Разделив последнее равенство на 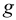, придём к окончательному виду

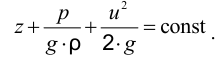
Полученное выражение называется интегралом Бернулли. Другое название интеграла Бернулли, которое применяется значительно чаще, уравнение Бернулли для элементарной струйки идеальной жидкости.

Уравнение Бернулли для элементарной струйки идеальной жидкости

Выше уравнение Бернулли для струйки идеальной жидкости получено строгими математическими методами, использующимися в классической гидромеханике. То же уравнение можно получить (нестрого), используя рассуждения, которые часто применяются в гидравлике.

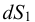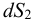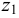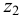Рассмотрим элементарную струйку идеальной жидкости при установившемся движении, в которой выделим два сечения 1-1 и 2-2 (рис. 47). Площади живых сечений потока обозначим и . Положение центров тяжести этих сечений относительно произвольно расположенной линии сравнения (нулевой линии) 0-0 характеризуется величинами и . Давления и скорости жидкости в этих сечениях имеют значения 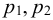и 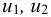соответственно.

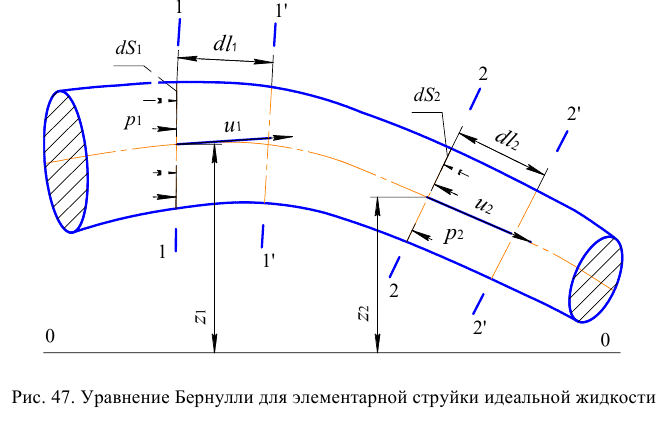
Будем считать, что движение струйки жидкости происходит только под действием силы давления (внутреннее трение в жидкости отсутствует), а давление обладает свойствами статического и действует по нормали внутрь рассматриваемого объёма.

Рассмотрим отсек струйки, ограниченный сечениями 1-1 и 2-2 (см. рис. 47).

За малый промежуток времени 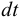частицы жидкости из сечения 1-1 переместятся в сечение 1′-1′ на расстояние, равное

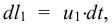
а частицы из сечения 2-2 в сечение 2-2′ на расстояние

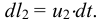
Согласно теореме о кинетической энергии изменение кинетической энергии тела (в данном случае выделенного отсека жидкости) равно сумме работ всех действующих на него сил.

Работу в данном случае производят силы давления, действующие в рассматриваемых живых сечениях струйки 1-1 и 2-2, а также силы тяжести. Тогда работа сил давления в сечении 1-1 будет положительна, т.к. направление силы совпадает с направлением скорости струйки. Она будет равна произведению силы 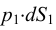на путь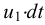

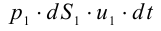
Работа сил давления в сечении 2-2 будет отрицательной, т.к. направление силы противоположно направлению скорости. Её значение

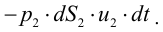
Полная работа, выполненная силами давления, имеет следующий вид

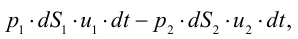
где произведение

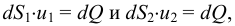
поэтому окончательно получим выражение для работы сил тяжести

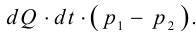
Работа сил тяжести равна изменению потенциальной энергии положения выделенного объёма жидкости при перемещении из сечения 1-1 в сечение 2-2. С учётом условия неразрывности потока и несжимаемости жидкости выделенные элементарные объёмы будут равны и, следовательно, будут равны их веса 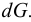. При перетекании из сечения 1-1 в сечение 2-2 центр тяжести выделенного объёма переместится на разность высот 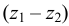и работа, произведённая силами тяжести, составит

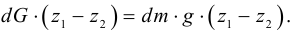
Но

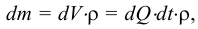
поэтому окончательно представим работу сил тяжести в гаком виде

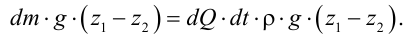
Проанализируем теперь изменение кинетической энергии рассматриваемого объёма элементарной струйки жидкости.

Приращение кинетической энергии выделенного объёма за 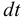равно разности его кинетических энергий в отсеках струйки 1-1-1-1 и 2-2-2-2′. А в пределах отсека 1-1-2-2 кинетическая энергия за рассматриваемый промежуток времени 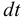не изменяется. Это приращение составит

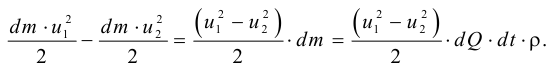
Приравнивая приращение кинетической энергии сумме работ сил тяжести и сил давления, придём к виду

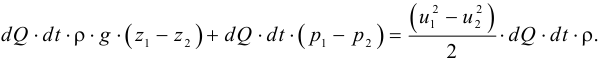
Разделив обе части полученного уравнения на 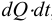, получим

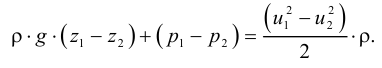
После упрощений в левой части уравнения оставляем все составляющие, имеющие индекс «1», а в правой — все составляющие, имеющие индекс «2»

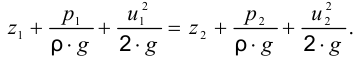
Если учесть, что сечения 1-1 и 2-2 выбраны произвольно, можно прийти к выводу, что сумма приведённых выше величин

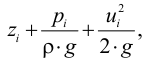
описывающих движение жидкости под действием сил давления и сил тяжести, есть величина постоянная для элементарной струйки, т.е.

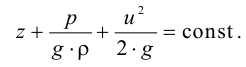
Таким образом, снова получено уравнение Бернулли (ранее полученное интегрированием уравнений Эйлера) для элементарной струйки невязкой жидкости при установившемся движении.

Уравнение Бернулли для потока идеальной жидкости

Поток идеальной жидкости, как указывалось ранее, можно представить совокупностью элементарных струек жидкости. Скорости по сечению потока неодинаковы, причём в середине потока скорости наибольшие, а к периферии они уменьшаются. Это означает, что различные струйки в одном сечении имеют различные значения кинетической энергии. Отсюда следует, что кинетическая энергия, определенная но скоростям элементарных струек 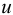, и кинетическая энергия, определенная но скоростям по средней скорости потока 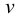, будет иметь разные значения. Выясним, какова эта разница. Кинетическая энергия элементарной струйки 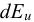равна

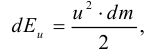
где 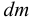— масса жидкости плотностью 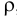, протекающей через живое сечение элементарной струйки 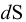со скоростью и за время 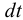, равная

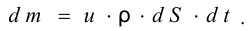
Проинтегрировав выражение для 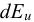, получим выражение для кинетической энергии потока идеальной жидкости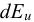

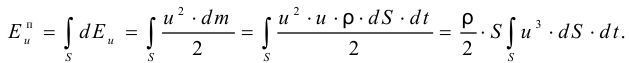
Если принять, что 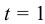, получим

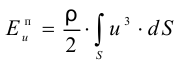
Последнее выражение определяет энергию потока, определенную по скоростям элементарных струек. А кинетическая энергия потока, определенная по средней скорости 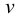, равна

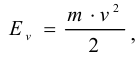
где 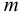— масса жидкости плотностью 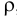, протекающей через живое сечение потока 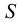со скоростью 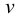за время 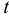, равная

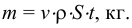
После подстановки при 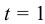окончательно получим

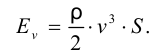
Отношение фактической кинетической энергии, протекающей через живое сечение потока (вычисленное по местным скоростям 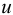) к фиктивной кинетической энергии (вычисленной по средней скорости 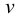) равно

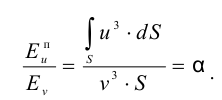
Полученная величина 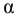носит название коэффициента кинетической энергии или коэффициента Кориолиса. При равномерном распределении скоростей его значение равно единице, а при неравномерном — всегда больше единицы, и для любого потока его значение находится в пределах от 1 до 2 и более. В общем случае в разных сечениях потока коэффициент 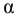будет иметь различные значения.

При переходе от местных скоростей к средней скорости изменяется только кинетическая энергия, а потенциальная энергия остается постоянной, т.е.

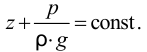
С учетом всего вышесказанного, уравнение Бернулли для потока идеальной жидкости примет вид

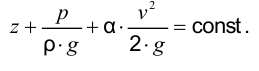
Уравнение Бернулли для потока реальной жидкости

При движении реальных жидкостей на их пути встречаются различные конструктивные препятствия, наличие которых обусловлено конструкцией и функциональным назначением трубопровода. К этим конструктивным препятствиям относятся: элементы запорной, регулирующей, измерительной аппаратуры, элементы отводов, поворотных колен, делителей потока и пр. Как правило, при движении через эти препятствия поток жидкости испытывает деформацию (сужение или расширение), при которой происходит искривление линий тока жидкости и активное вихреобразование. На образование и гашение вихрей затрачивается часть механической энергии жидкости.

Кроме того, в реальной жидкости, в отличие от идеальной, присутствуют силы вязкого трения. Поэтому при движении происходит внутреннее трение слоев жидкости друг о друга. Внешнее трение проявляется в том, что жидкость испытывает трение при скольжении вдоль шероховатых стенок по всей длине трубопровода. На это внутреннее и внешнее трение также затрачивается часть энергии потока. Эта энергия, как и при любом трении, преобразуется в тепловую энергию.

Из-за этих потерь энергия потока жидкости по длине потока и в его направлении постоянно уменьшается. Поэтому энергия потока жидкости в вышерасположенных сечениях (по ходу движения) всегда больше энергии жидкости в нижерасположенных сечениях (по ходу движения) на величину потерь напора (или давления).

Если рассмотреть два соседних сечения 1-1 и 2-2 трубопровода, то потери гидродинамического напора 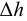составят

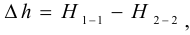
где 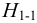— напор в первом сечении потока жидкости, м;

— напор во втором сечении потока, м;

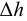— потери напора, энергия, потерянная каждой единицей веса движущейся жидкости на преодоление сопротивлений при движении жидкости от сечения 1-1 до сечения 2-2.

С учётом потерь энергии уравнение Бернулли для потока реальной жидкости будет выглядеть

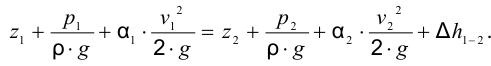
Индексами «1» и «2» обозначены характеристики потока в сечениях 1-1 и 2-2.

Если учесть, что характеристики потока и 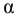зависят от геометрии потока, которая для напорных потоков определяется геометрией трубопровода, то становится понятно, что потери энергии (напора) в разных трубопроводах будут изменяться неодинаково. Показателем изменения напора потока является гидравлический уклон I, который характеризует потери напора на единице длины потока. Физический смысл гидравлического уклона — интенсивность рассеяния энергии по длине потока. Другими словами, величина I показывает как быстро трубопровод поглощает энергию потока, протекающего в нём

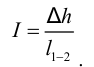
Изменение энергии по длине потока удобно проследить на графиках. Из уравнения Бернулли для потока реальной жидкости (закона сохранения энергии) видно, что гидродинамическая линия для потока реальной жидкости (с одним источником энергии) всегда ниспадающая. То же справедливо и для пьезометрической линии, но только в случае равномерного движения, когда скоростной напор 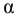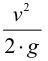постоянен, а уменьшение напора происходит только за счёт изменения потенциальной энергии потока, главным образом за счёт уменьшения давления .

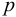Геометрическая и энергетическая интерпретация уравнения Бернулли

Уравнение для потока реальной жидкости устанавливает связь между скоростью движения, давлением и геометрическим положением частиц жидкости для двух сечений струйки и называется уравнением энергетического баланса движущейся жидкости или уравнением Бернулли для элементарной струйки идеальной жидкости.

Для определения геометрического смысла уравнения Бернулли рассмотрим ноток движущейся жидкости относительно произвольно выбранной плоскости сравнения 0 — О (рис. 48). Все слагаемые уравнения Бернулли имеют размерность длины и их можно изобразить графически.

Выберем три сечения 1-1; 2-2; 3-3, центры тяжести которых относительно произвольно выбранной горизонтальной плоскости сравнения 0-0 расположены на высотах 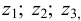, Эти высоты принято называть геометрическими напорами. Если домножить и разделить размерность геометрических напоров, то есть метры на единицу веса (ныотон) получим

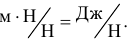
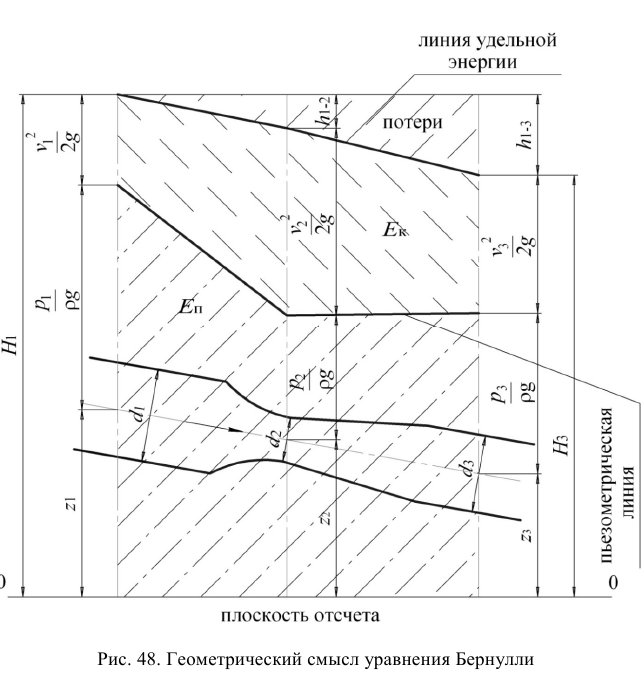
Таким образом, получается отношение единицы энергии к единице веса или единица удельной энергии, отнесенной к единице веса. А значит можно сказать, что геометрический напор выражает удельную потенциальную энергию положения частицы жидкости, поднятой от плоскости сравнения на высоту z.

Давления жидкости в рассматриваемых сечениях соответствуют пьезометрическим высотам

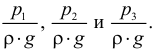
Так как размерность всех членов уравнения Бернулли одинакова, можно говорить, что пьезометрическая высота выражает удельную потенциальную энергию давления в рассматриваемом сечении элементарной струйки.

Третьи составляющие уравнения

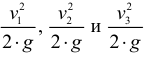
и характеризуют удельную кинетическую энергию жидкости и называются скоростными напорами или скоростными высотами. Данную величину можно представить как высоту, на которую поднимется жидкость, начавшая двигаться вертикально со скорость и при отсутствии сопротивления движению.

Сумма геометрического напора и пьезометрической высоты называется пьезометрическим напором и характеризует полную удельную потенциальную энергию жидкости или гидростатический напор

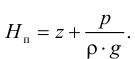
Если плавной кривой соединить точки, соответствующие значениям пьезометрических напоров в выбранных сечениях, то получим пьезометрическую линию (см. рис. 48), характеризующую полную удельную потенциальную энергию жидкости.

Сумма трех членов

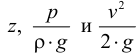
называется полным гидродинамическим напором Н

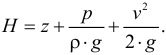
Линия, соответствующая значениям гидродинамических напоров, называется напорной линией или линией удельной энергии жидкости.

Изображение, представленное на рис. 48 называется графиком напоров.

Важный вывод следует из уравнения Бернулли. С уменьшением площади живого сечения потока происходит увеличение скорости, то есть рост удельной кинетической энергии. Так как запас энергии жидкости должен оставаться постоянным (без учета потерь напора на преодоление гидравлических сопротивлений), увеличение удельной кинетической энергии потока вызовет неизбежное уменьшение удельной потенциальной энергии давления. Проще говоря, уменьшение площади живого сечения потока вызывает увеличение скорости и падение давления. И наоборот, увеличение площади живого сечения потока вызывает уменьшение скорости и повышение давления. Откуда следует парадоксальное, на первый взгляд, заключение: в самом узком сечении потока давление минимальное, а в самом широком сечении давление максимальное.

Скоростной напор

Для измерения скорости движения жидкости и газа в рассматриваемых точках потока широко используется работающая на принципе уравнения Бернулли трубка Пито (рис. 49), верхний конец которой открыт в атмосферу, а нижний конец изогнут навстречу потоку под углом 90°.

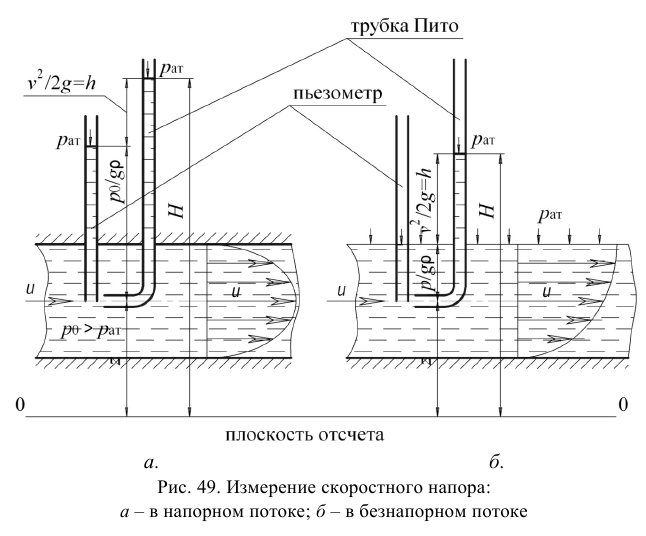
На рис. 49, а показано, как измеряется скорость в напорном потоке, где давление отлично от атмосферного. Пьезометр, присоединенный к трубе, но которой движется жидкость покажет величину пьезометрической высоты 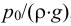, соответствующей избыточному давлению в трубе 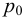. Уровень жидкости в скоростной трубке всегда устанавливается выше, чем в пьезометре. А разница в показаниях пьезометра и трубки Пито 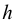соответствует величине скоростного напора 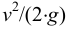. Откуда скорость жидкости в рассматриваемом сечении составит

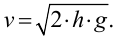
Для измерения скорости в безнапорном потоке (рис. 49, 6) достаточно только трубки Пито, поскольку уровень жидкости в ней показывает величину скоростного напора, соответствующего данной скорости.

Режимы течения жидкостей

Многочисленные экспериментальные исследования показали, что потери энергии при движении жидкости существенно зависят от характера движения частиц жидкости в потоке и от режима движения жидкости.

Еще в 1880 г. Д. И. Менделеев в работе «О сопротивлении жидкостей и воздухоплавании» указал на наличие различных видов движения жидкости, которые отличаются друг от друга характером зависимостей сил трения от скорости движения. Более подробно эти виды движения жидкостей были изучены английским физиком Осборном Рейнольдсом в 1883 г.

Наглядно особенности режимов движения можно наблюдать на специальной опытной установке, схема которой показана на рис. 50. К баку Б достаточно больших размеров, наполненному жидкостью, присоединена стеклянная труба Т; вход в трубу сделан плавным; в конце трубы установлен кран К для регулирования расхода потока. Измерение расхода выполняется с помощью мерного бака М и секундомера.

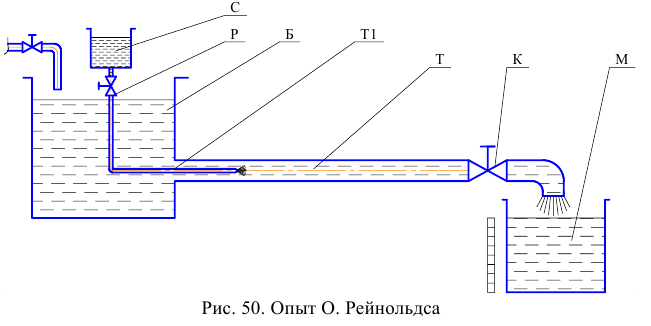
Над баком; Б расположен сосуд С, наполненный раствором краски, плотность которого близка к плотности жидкости в потоке. По трубке Т1 краска вводится в поток. Расход краски регулируется краном Р. При открытом кране К в трубе Т установится некоторая скорость потока (высота уровня жидкости в баке поддерживается постоянной). Если открыть кран Р, то в трубу Т начнет поступать краска. При малой скорости v потока в трубе Т краска образует прямолинейную и резко выделяющуюся не смешивающуюся с окружающей жидкостью струйку. Заметного обмена частицами между окрашенной струйкой и окружающей ее жидкостью не происходит. Если ввести в жидкость краску несколькими струйками, то все они будут двигаться, не смешиваясь с остальной массой жидкости. Это свидетельствует о том, что в прямой стеклянной трубе Т (при данной степени открытия крана) жидкость движется отдельными не перемешивающимися между собой слоями. Линии тока при этом прямолинейны и устойчивы (рис. 51, а).

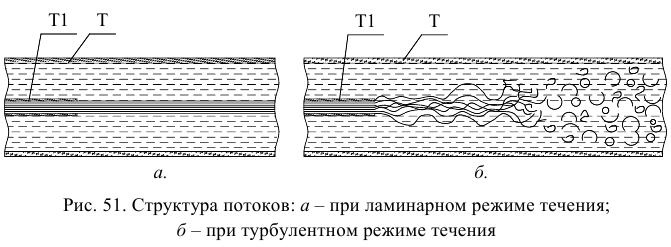
При некотором большем открытии крана окрашенная струйка начинает искривляться и становится волнообразной. Это может происходить только в результате изменений во времени (пульсации) векторов местных скоростей в потоке.

При дальнейшем увеличении скорости потока в трубе Т струйка распадается на отдельные хорошо видные вихри, происходит перемешивание окрашенной струйки со всей массой текущей жидкости (рис. 51, 6).

Слоистое движение жидкости, при котором отсутствуют изменения (пульсации) местных скоростей, приводящие к перемешиванию жидкости, называют ламинарным (от латинского слова «lamina» слой).

Движение жидкости, при котором происходят изменения (пульсации) местных скоростей, приводящие к перемешиванию жидкости, называют турбулентным (от латинского слова «turbulentus» — беспорядочный).

Применяются также термины ламинарный режим движения, турбулентный режим движения.

При постепенном закрывании крана явление повторяется в обратном порядке. Однако переход от турбулентного режима к ламинарному происходит при скорости меньше той, при которой наблюдается переход от ламинарного движения к турбулентному. Скорость потока, при которой происходит смена режима движения жидкости, называется критической. Рейнольдсом было обнаружено существование двух критических скоростей: одной — при переходе ламинарного режима движения в турбулентный режим, она называется верхней критической скоростью 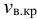, другой — при переходе турбулентного режима движения в ламинарный режим, она называется нижней критической скоростью 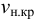. Опытным путем доказано, что значение верхней критической скорости зависит от внешних условий опыта: постоянства температуры, уровня вибрации установки и т. д. Нижняя критическая скорость в широком диапазоне изменения внешних условий остается практически неизменной. В опытах было показано, что нижняя критическая скорость для потока в цилиндрической трубе круглого сечения пропорциональна кинематической вязкости 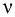и обратно пропорциональна диаметру трубы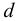

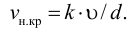
Коэффициент пропорциональности к оказался одинаковым для различных 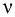и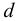

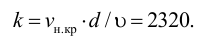
В честь Рейнольдса этот коэффициент был назван критическим числом Рейнольдса и обозначен .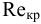

Для любого потока по известным 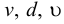можно вычислить число Рейнольдса 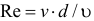и сравнить его с критическим значением 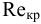. Если

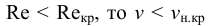
и режим движения жидкости ламинарный. Если

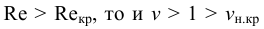
и режим движения, как правило, турбулентный. Однако создание специальных условий движения жидкости (плавный вход в трубу, изоляция от динамических воздействий и т. п.) позволяло в лабораторных условиях получать и наблюдать ламинарное движение в трубах при числах 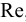, доходивших до 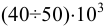и более. Но такое ламинарное движение очень неустойчиво, и достаточно воздействия малого возмущения, чтобы произошел переход в турбулентное движение.

Таким образом, в общем случае режим движения жидкости определяется безразмерным комплексом

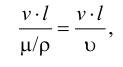
состоящим из четырех величин: динамической вязкости 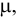плотности жидкости 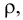характерного геометрического размера живого сечения 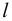и средней скорости потока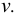

Этот комплекс называется числом Рейнольдса и обозначается символом 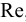. Физический смысл числа Рейнольдса состоит в том, что оно выражает отношение сил инерции к силам вязкости

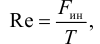
где 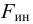— силы инерции, Н;

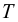— силы трения (вязкости ), Н,

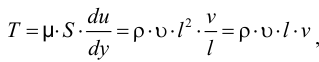
где 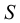— площадь живого сечения, .

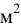Тогда получим

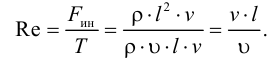
При преобладании в потоке сил вязкости — режим ламинарный, при преобладании сил инерции — режим турбулентный.

Отнесенные к единице объема силы инерции, действующие в установившемся потоке, имеют порядок

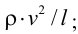
силы трения, также отнесенные к единице объема, —

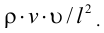
Очевидно, что отношение указанных сил и дает число

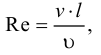
где 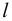— характерный поперечный размер живого сечения, м.

Поскольку характерный размер живого сечения выбирается произвольно, число Рейнольдса имеет нижний индекс, указывающий выбранную характерную линейную величину. Чаще всего в качестве характерных линейных величин принимают диаметр трубы 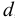, гидравлический радиус 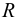или глубину жидкости в открытом русле (канале) .

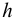Тогда

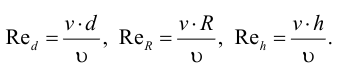
Число 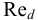в дальнейшем будем обозначать 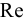без индекса.

В расчетах обычно принимают для цилиндрических круглых труб критическое значение .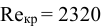

На конфузорных (сужающихся) участках труб значение числа Рейнольдса 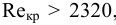а на расширяющихся участках (диффузорах) .

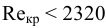Для открытых русл

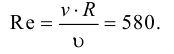
В опытах Рейнольдса было обнаружено, что переход ламинарного движения в турбулентное происходит не мгновенно и не одновременно по всей длине трубы. При числах 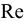, близких к 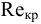(но меньше 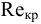), на отдельных участках трубы периодически возникают турбулентные области («пробки»), которые сносятся вниз по направлению движения. На месте возникновения «пробки» вновь восстанавливается ламинарное движение. Происходит перемежающаяся смена ламинарного и турбулентного движений в данном сечении. При дальнейшем увеличении числа Re участки турбулентного движения полностью заполняют трубу.

Коэффициент перемежаемости 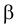равен отношению времени, в течение которого в данном сечении наблюдалось турбулентное движение, ко всему времени наблюдений; если 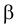= 0, движение ламинарное, если 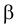= 1, движение полностью турбулентное.

При

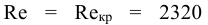
движение становится полностью турбулентным (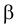 = 1) на длине более тысячи диаметров от входа в трубу.

В природе и технике турбулентное движение жидкости наблюдается чаще, чем ламинарное. Области ламинарного движения движение вязких жидкостей типа масел по трубам и в механизмах, движение грунтовых вод (но оно может также быть и турбулентным), движение в капиллярах (в том числе и движение крови в живых организмах). В настоящее время не существует строгого научно доказанного объяснения этому явлению, однако наиболее достоверной гипотезой считается следующая: смена режимов движения жидкости определяется отношением сил инерции к силам вязкости в потоке жидкости. Если преобладают первые, то режим движения турбулентный, если вторые — ламинарный.

Турбулентные потоки возникают при высоких скоростях движения жидкости и малой вязкости, ламинарные потоки возникают в условиях медленного течения и в вязких жидкостях. На практике в различных газопроводах, водопроводах и подобных им системах чаще встречаются турбулентные потоки даже при скоростях менее 1 м/с. В гидросистемах технологического оборудования, в которых в качестве рабочих жидкостей используются минеральные масла, турбулентный режим возникает при скоростях более 15 м/с, тогда как при проектировании таких систем чаще всего предусматривают скорости 4-5 м/с. Режим движения в таких трубопроводах, как правило, ламинарный.

Так как силы инерции и силы вязкости в потоке жидкости зависят ог многих причин, то при скоростях, близких к критической, могут возникать переходные режимы, при которых наблюдаются неустойчивое ламинарное или турбулентное движение.

Распределение скоростей при ламинарном режиме

Напомним, что ламинарное течение — это упорядоченное слоистое течение, математическое описание которого основано на законе трения Ньютона.

При ламинарном режиме течения жидкости местные скорости во всех точках потока не подвержены пульсациям, т.е. не изменяются во времени.

В результате многочисленных экспериментов была получена следующая картина распределения скоростей но живому сечению потока — рис. 52.

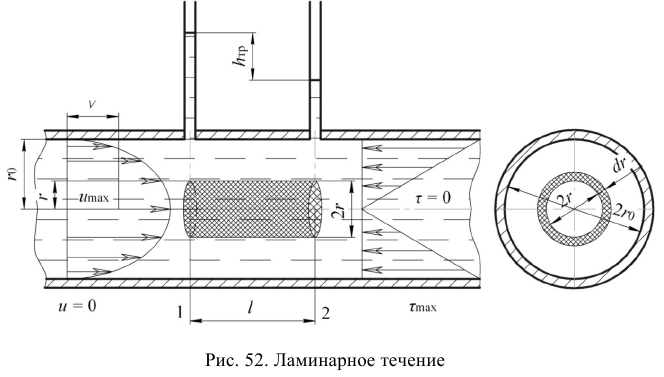
Непосредственно на стенке скорость равна нулю 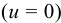а по мере удаления от стенки, т.е. приближения к оси трубы, скорости возрастают, достигая максимума на оси.

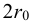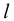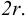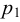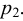Для начала рассмотрим установившееся ламинарное течение в круглых трубах. В трубе диаметром выделим цилиндрический объём жидкости между сечениями 1 и 2 длиной и диаметром Отметим, что давления в сечениях 1 и 2 соответственно равны и . Распределение скоростей по сечению потока на всей длине трубы одинаково, поэтому одинаково и значение коэффициента кинетической энергии 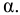На рассматриваемый объём, движущийся со скоростью 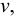действуют силы давления (на торцовые поверхности) и силы сопротивления, вызванные вязким трением на боковой поверхности. Потери напора между рассматриваемыми сечениями можно выразить

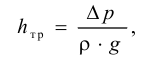
а уравнение сил, действующих на выделенный объём, будет выглядеть

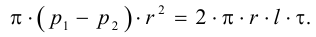
Выразив отсюда 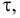получим

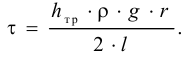
Из последней формулы следует, что касательные напряжения трения линейно зависят от радиуса грубы. С другой стороны, касательные напряжения по закону Ньютона равны

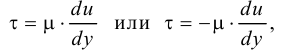
т.к. разница скоростей между соседними потоками жидкости зависит от радиуса 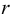.Знак « — » в формуле означает, что отсчёт по 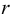направлен от оси к стенке, а при отсчете по у — от стенки к оси потока. Тогда

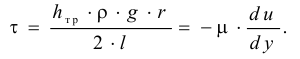
Из этого соотношения можно найти приращение скорости

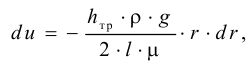
т.е. при увеличении радиуса скорость уменьшается, что соответствует эпюре скоростей.

После интегрирования, получим

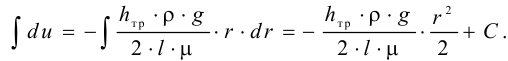
Постоянную интегрирования 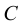легко определить из известных условий у стенки трубы, т.е. при

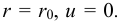
С учётом этих условий 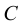примет вид

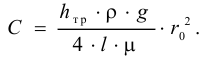
И тогда скорость в ламинарном потоке в зависимости от радиуса (а практически это скорость движения цилиндрического слоя жидкости, состоящего из элементарных струек, расположенных на одном радиусе в цилиндрическом потоке) будет описываться формулой

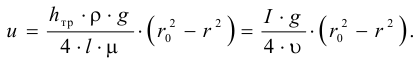
Таким образом, скорости при ламинарном движении распределяются по квадратичному закону. Максимальное значение скорости достигается в центре потока при 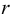= 0 и составляет

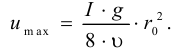
Касательные напряжения у стенки грубы 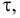зависят от вязкости, средней по сечению скорости, диаметра трубы и определяются как

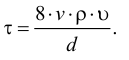
Возникновение турбулентного течения жидкости

Если на каком-то участке трубопровода существует турбулентный поток, то это не значит, что такой же характер сохраняется во всей трубе. На различных участках трубопровода и даже на одних и тех же участках в разные периоды времени поток может иметь различный характер. Это может определяться либо различными диаметрами трубопроводов, либо изменением скорости течения жидкости. Во всех случаях при возникновении условий турбулентного режима он устанавливается в трубе не мгновенно. Это происходит в течение некоторого времени на участке трубы определённой длины. Рассмотрим процесс возникновения турбулентного режима движения (рис. 53)

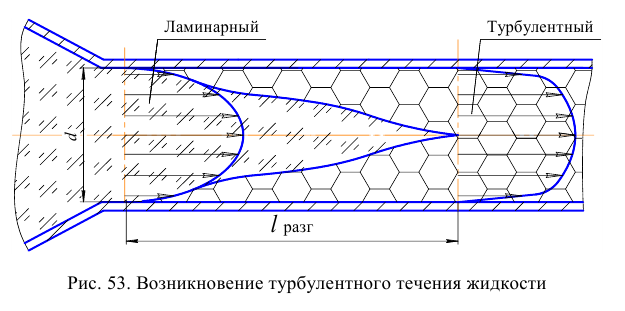
Переход к турбулентному режиму может происходить из ламинарного, например, в результате плавного или внезапного изменения диаметра трубы Такой же переход возможен за счёт изменения скорости движения жидкости. К образованию турбулентного режима может приводить также и изменение формы потока жидкости.

Кроме перечисленных возможны и другие причины, особенно при режимах, характеризующихся числами Рейнольдса, близкими к критическому. На основании опыта установлено следующее. Когда создаются условия для такого перехода, например, сужение проходного сечения грубы достигает значения, при котором поток может стать турбулентным, по периферии потока ламинарный слой нарушается и дальше по течению развивается турбулентный пограничный слой.

Толщина этого слоя из-за турбулентного перемешивания достаточно быстро увеличивается, и турбулентный поток заполняет всё сечение трубопровода. Участок, на котором происходит превращение ламинарного режима движения в турбулентный, называется разгонным участком. Его длина 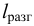(см. рис. 53) по экспериментальным данным равна

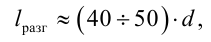
где 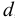— диаметр трубопровода, м.

Теория из учебников тут.

Возникновение ламинарного режима

В реальных гидросистемах при ламинарном режиме течения жидкости в круглых трубах там, где на пути потока встречаются местные сопротивления, в которых ноток испытывает деформацию, характер потока меняется, и режим движения становится турбулентным.

Однако после прохождения такого участка при входе жидкости в прямую трубу при соответствующей скорости устанавливается параболическое распределение скоростей. Поток снова стремится к ламинарному режиму движения. Происходит это не моментально, а в течение некоторого времени на отрезке трубы определённой длины. Такой отрезок называют начальным участком ламинарного течения .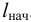

Длину такого участка можно определить из формулы Шиллера

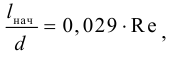
где 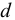— диаметр трубы, м.

Отсюда, если в качестве 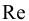взять критическое число Рейнольдса легко получить, что максимально возможная длина такого участка равна

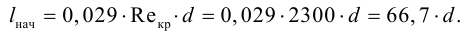
Потери энергии на этом участке будут несколько больше, чем в остальной части трубы. С учётом этого формула для расчёта потерь напора на трение 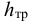при ламинарном движении в круглых гладких трубах принимает вид

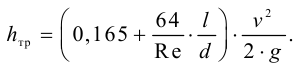
Для коротких труб такое уточнение потерь напора может иметь существенное значение. Для длинных трубопроводов величину коэффициента 0,165 можно не учитывать.

Распределение скоростей при турбулентном режиме

Для турбулентного течения характерны пульсации скоростей и давлений в процессе движения. Если с помощью особо чувствительного прибора-самописца измерить и записать пульсации, например, скорости во времени, то получится картина, подобная показанной на рис. 54. Величина скорости беспорядочно колеблется около некоторого осредненного значения, которое в данном случае остается постоянным. Для упрощения расчетов турбулентных потоков ввели понятие усредненной местной скорости так как скорости 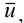хотя и пульсируют, но колеблются относительно некоторого постоянного значения

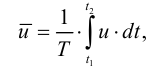
где 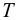— достаточно большой интервал времени, с.

Траектории частиц, проходящие через данную неподвижную точку пространства в разные моменты времени, представляют собой кривые линии различной формы, несмотря на прямолинейность грубы. Характер линий тока в трубе в данный момент времени также отличается большим разнообразием (рис. 55).

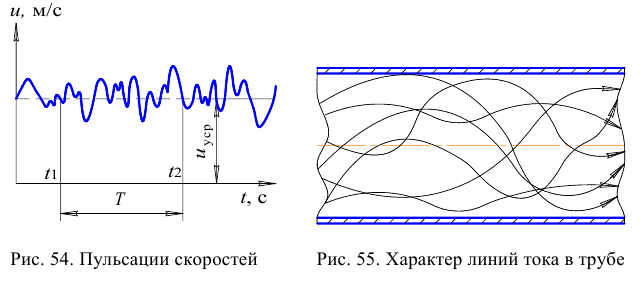
Таким образом, строго говоря, турбулентное течение является неустановившимся течением, так как величины скоростей и давлений, а также траектории частиц меняются во времени. Однако его можно рассматривать как установившееся при условии, что осредненные по времени значения скоростей и давлений, а также величина полного расхода потока не меняются с течением времени. Такое течение встречается на практике достаточно часто.

Многочисленными опытами установлено, что турбулентный поток, как правило, не соприкасается со стенками грубы, а занимает только центральную часть. Структура турбулентного потока иная, чем при ламинарном режиме течения (рис. 56).

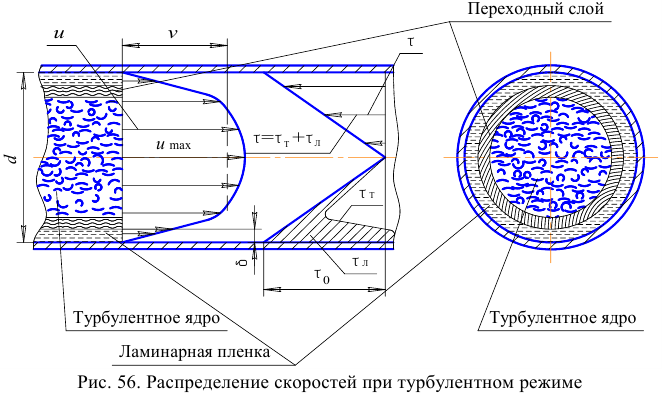
Непосредственно у стенки трубы обычно имеется ламинарный слой. Это весьма тонкий слой жидкости, движение в котором является наиболее замедленным, слоистым и происходит без перемешивания, т. е. ламинарным. В пределах этого слоя скорость резко нарастает от нуля на стенке до некоторой конечной величины на границе слоя. Причём внешняя часть этого слоя, соприкасающаяся с поверхностью трубы, неподвижна (имеет нулевую скорость), а его внутренняя часть, непосредственно взаимодействующая с потоком, имеет скорость, соизмеримую со средней скоростью жидкости в данном сечении.

Таким образом, турбулентный поток движется как бы в трубе из ламинарного слоя той же жидкости. Толщина ламинарной пленки весьма мала и уменьшается с увеличением скорости, а значит и числа Рейнольдса. Приближенно толщину ламинарной пленки можно определить по эмпирической зависимости

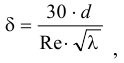
где 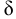— толщина ламинарной пленки, м; 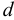— диаметр трубы, м;

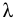— коэффициент гидравлического сопротивления трения. Можно считать, что скорость жидкости внутри этого слоя по толщине меняется но линейному закону. Надо также отметить, что число Рейнольдса 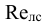(число Рейнольдса для ламинарного слоя), подсчитанное но толщине слоя 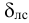, скорости внутренней части ламинарного слоя 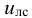и кинематическому коэффициенту вязкости и, есть величина постоянная

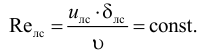
Эта величина имеет постоянное значение для любых турбулентных потоков. Поэтому при увеличении скорости потока растёт скорость ламинарного слоя, а его толщина уменьшается. При больших значениях 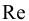(больших скоростях) ламинарный слой практически исчезает.

За ламинарной пленкой расположен переходный слой, где происходит превращение ламинарного движения в турбулентное движение. Пограничный слой имеет толщину ог 0,1 мм до нескольких миллиметров. Всю остальную часть площади живого сечения потока занимает турбулентное ядро течения. В переходном слое ламинарное течение нарушается перемешиванием частиц. Совокупность ламинарной пленки и переходного слоя называется пограничным слоем.

В турбулентном ядре присутствуют все признаки турбулентного режима течения с активным перемешиванием частиц и колебаниями скоростей и давлений. В турбулентном ядре благодаря интенсивному поперечному перемешиванию и выравниванию скоростей частиц осредненные скорости изменяются сравнительно мало, и их распределение по основной части течения оказывается значительно более равномерным, чем при ламинарном режиме. Средняя скорость в потоке оказывается равной (0,75 — 0,9)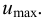

Переход потока в турбулентное состояние приводит к сильному возрастанию сопротивления трубопровода, что связано с увеличением касательных напряжений трения. В турбулентном ядре, где градиенты усредненной скорости невелики, касательные напряжения вязкостного трения играют незначительную роль. Основная часть сопротивления создается здесь так называемыми турбулентными касательными напряжениями, которые возникают из-за непрерывных поперечных перемещений (беспорядочного перемешивания) частиц. Обмен частицами между соседними слоями сопровождается соответствующим увеличением или уменьшением количества движения этих частиц (турбулентный обмен количеств движения). Так как при этом более быстрые слои тормозятся, а более медленные ускоряются, то между ними возникает динамическое взаимодействие, которое проявляется в виде турбулентных касательных напряжений.

Распределение осредненных турбулентных 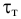и вязкостных (ламинарных) 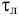касательных напряжений изображено схематично на рис. 56. Полное осредненное касательное напряжение 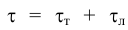подчиняется линейному закону. В переходном слое по мере уменьшения пульсаций и возрастания градиента осредненной скорости происходит резкое уменьшение 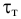почти до нуля и увеличение 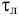до его значения в ламинарной пленке, равного касательному напряжению 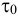на стенке. В ламинарной пленке турбулентные касательные напряжения практически отсутствуют, а вязкостное напряжение (почти постоянное по толщине слоя) весьма велико, гак как градиент скорости имеет большую величину.

Несмотря на то, что в общем случае турбулентное движение жидкости является неустойчивым, если рассматривать некоторые усредненные по времени характеристики потока, среднюю скорость, среднее распределение скоростей по сечению, среднее давление, средние величины пульсаций, а также среднее значение расхода, то во многих случаях они могут оказаться постоянными. Именно такие характеристики мы и будем использовать при описании турбулентных потоков.

Эти страницы вам могут пригодиться:

1. Учебник по гидравлике
2. Формулы по гидравлике
3. Сборник задач по гидравлике
4. Курсовая работа по гидравлике