Оглавление:
Гидравлика
Гидравлика — это наука о законах движения и равновесия жидкостей и о том, как эти законы могут быть применены для инженерных задач, что, по сути, является техническим применением гидромеханики. В настоящее время различные гидравлические устройства, основанные на использовании гидравлических законов, применяются практически во всех отраслях водного хозяйства.
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Основные физические свойства жидкости
Общие сведения:
Жидкость — это материальная среда (вещество), обладающая свойством текучести, т.е. способностью неограниченно деформироваться под действием приложенных сил. Данное свойство обусловлено диффузией молекул, благодаря чему жидкость не имеет собственной формы и принимает форму того сосуда, в котором она находится.
Жидкости подразделяют на две группы: капельные — практически не сжимаемые и газообразные — легко сжимаемые. Газообразные жидкости, в отличие от капельных, не имеют свободной поверхности раздела между жидкостью и газообразной средой.
Возможно эта страница вам будет полезна:
| Предмет гидравлика |
Для упрощения рассматриваемых явлений и вывода ряда закономерностей в гидравлике, как и в механике твёрдого тела, вводят ряд допущений и гипотез, т.е. прибегают к модельной жидкости. В гипотезе сплошной среды жидкость рассматривается как непрерывная сплошная среда (континуум), полностью занимающая все пространство без разрывов и пустот. Правда, эта гипотеза не пригодна при изучении сильно разреженных газов и кавитации [1], но она позволяет рассматривать все механические характеристики жидкости (плотность, скорость движения, давление) как функции координат точки в пространстве и во времени. Следовательно, любая функция, которая характеризует состояние жидкости, непрерывна и дифференцируема, т.е. при решении задач гидравлики можно использовать математические зависимости и ЭВМ.
Плотность жидкости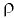 
— масса 
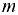единицы объёма 
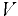однородной жидкости:
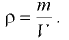
Размерность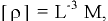 
где 
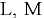— обобщенные обозначения единиц длины и массы. Единицей плотности в системе СИ является 
.
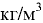Значения плотности наиболее распространенных жидкостей приведены в прил. 1. Иногда в справочниках приводится относительная плотность вещества.
Относительная плотность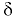 
— отношение плотности рассматриваемого вещества к плотности стандартного вещества в определенных физических условиях:
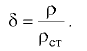
В качестве стандартного вещества принимают: для твёрдых тел и капельных жидкостей — дистиллированную воду плотностью 1 000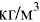 
при температуре 277 К (4 °С) и давлении 101,3 кПа (760 мм рт. ст.); для газов -атмосферный воздух плотностью 1,2 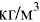при температуре 293 К (20 °С), давлении 101,3 кПа и относительной влажности 50 % (стандартные условия) [2].
Для измерения плотности служат приборы: пикнометры, ареометры.
Сжимаемость — способность жидкости изменять свой объём 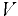, а следовательно, и плотность при изменении давления 
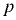и (или) температуры 
.
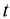Плотность капельных жидкостей при температуре и давлении, отличных от начальных,
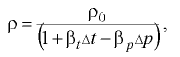
где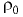 
— плотность жидкости при начальных температуре и давлени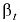и; 
и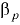 
— коэффициенты температурного расширения и объёмного сжатия, подставляющие собой относительные изменения объёма жидкости 
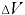при изменении соответственно температуры 
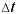или давления 
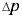на одну единицу (коэффициенты приведены в прил. 1 при начальных условиях),
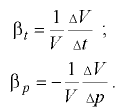
Знак «минус» в формуле указывает на то, что при увеличении давления объем жидкости уменьшается
Величина, обратная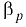 
, называется объёмным модулем упругости жидкости:
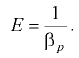
Значения коэффициентов 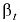и 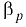, а также модуля упругости 
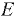наиболее распространенных жидкостей приведены в прил. 1. При температуре 20 °С средние значения для воды
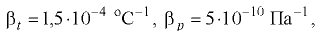
для минеральных масел, применяемых в гидроприводах,
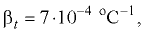
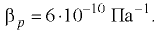
При решении многих практических задач изменением плотности капельных жидкостей при изменении температуры и давления обычно пренебрегают (за исключением задач о гидравлическом ударе, устойчивости и колебании гидравлических систем и других, в которых приходится учитывать сжимаемость жидкости, а также ряда тепловых расчётов, в которых необходим учёт изменения температуры жидкости).
Плотность газообразных жидкостей (газов) в значительной степени зависит от температуры и давления. Используя известное уравнение Клапейрона-Менделеева (уравнение состояния идеального газа)
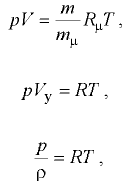
где 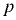— абсолютное давление; 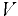— объём; 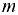— масса; 
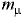— молярная масса; 
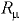— универсальная газовая постоянная, равная 8.314 Дж/(моль К); 
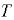— абсолютная температура; 
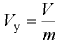— удельный объём; 
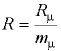— газовая постоянная (для воздуха 
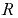= 286 Дж (кг • К), для метана 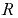= 518 Дж'(кг • К)), можно установить зависимость плотности газа от температуры и давления:
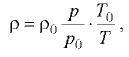
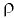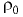где и — плотности газа соответственно при новых давлении 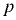и температуре 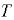и начальных давлении 
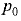и температуре 
.
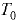В состоянии покоя характерным параметром сжимаемости жидкости служит скорость распространения в ней звуковых колебаний (скорость звука)
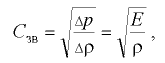
где 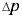— приращение давления; 
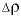— приращение плотности жидкости.
При температуре воды 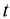= 10 °С и модуле упругости 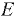= 2,03-109 Па скорость звука в воде
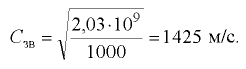
Чем больше скорость звука, тем меньше сжимаемость жидкости и наоборот [3].
Для движущейся жидкости её сжимаемость оценивают числом Маха, т.е. отношением скорости потока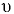 
к скорости звука 
:
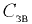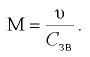
Если скорость движения жидкости мала по сравнению со скоростью распространения в ней звука, т.е. число Маха значительно меньше единицы, то, независимо от абсолютного значения скорости звука, капельную жидкость при таком движении считают практически несжимаемой.
Растворимость — способность жидкости поглощать и растворять газы. Объём газа, растворённого в капельной жидкости,
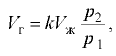
где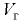 
— объём газа при начальном давлении ; 
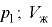— объём жидкости при конечном давлении 
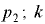— коэффициент растворимости (например, при 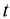= 20 °С коэффициент растворимости воздуха в воде равен 0,016; в минеральном масле -0.08…0,1).
Местное понижение давления в каком-нибудь узле гидросистемы (во всасывающих линиях насосов, в местных сопротивлениях с высокими скоростями потоков) влечёт за собой выделение в этом месте газа в виде мельчайших пузырьков и образование пены, которая может появляться также при засасывании воздуха в гидросистему через неплотности или при перемешивании жидкости в резервуаре (баке). Наличие газа, и особенно пены, уменьшает плотность рабочей жидкости, увеличивает её сжимаемость, нарушает сплошность потока и нормальную работу гидросистем.
Обычно в рабочей жидкости при работе гидропривода содержится до 6 % нерастворёнпого воздуха (по объёму ); после отстаивания в течение суток содержание воздуха уменьшается до 0,01…0,02 % [4]. При давлении до 0,5 МПа в результате влияния нерастворённого воздуха модуль упругости рабочей жидкости резко снижается, поэтому в гидросистемах рекомендуется иметь подпор в сливных линиях.
Испаряемость жидкостей характеризуется давлением насыщенных паров. Давлением насыщенных паров считают то абсолютное давление, при котором жидкость закипает при данной температуре. Следовательно, минимальное абсолютное давление, при котором вещество находится в жидком состоянии, равно давлению насыщенных паров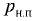 
, величина которого зависит от рода жидкости и её температуры.
Парообразование — свойство капельных жидкостей изменять своё агрегатное состояние на газообразное. Парообразование, происходящее лишь на поверхности капельной жидкости, называется испарением. Парообразование по всему объёму жидкости называется кипением, оно происходит при определённой температуре, зависящей от давления [5].
При давлении в жидкости, равном давлению насыщенного пара 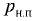при данной температуре, происходит изменение состава жидкости, в ней образуются пузырьки и даже полости, наполненные паром и растворённым газом. Пузырьки при достижении свободной поверхности жидкости лопаются, пар улетучивается — происходит кипение жидкости.
В жидкости, находящейся в замкнутом пространстве без свободной поверхности, пузырьки пара и газа остаются в ней, и при превышении давления насыщенного пара снова происходит качественное изменение — пар конденсируется, газы растворяются в капельной жидкости. Происходит смыкание полостей (пузырьков), что вызывает рост давления (до нескольких МПа), сопровождающийся характерным шумом. Это явление называется кавитацией.
Кавитация в гидроприводах явление крайне вредное, вызывает шум, вибрацию и эрозию (разрушение) стенок труб и проточных частей гидромашин.
Капиллярность — способность капельной жидкости, находящейся в трубке малого диаметра (капилляре), подниматься выше свободной поверхности в резервуаре (рис. 1.1, д), образуя вогнутый мениск, если жидкость смачивает стенки трубы, или опускаться ниже — свободной поверхности (рис. 1.1, б), образуя выпуклый мениск, если жидкость не смачивает стенки трубки. Эта способность обусловлена её поверхностным натяжением и молекулярными силами взаимодействия между жидкостью и стенками трубки.
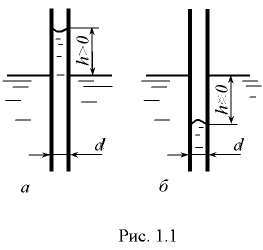
Высота поднятия или опускания жидкости в трубке, мм,
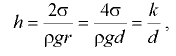
где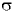 
— поверхностное натяжение; 
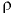— плотность жидкости; 
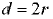— внутренний диаметр трубки, мм; 
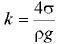— постоянная для каждой конкретной жидкости: для воды 
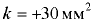, для спирта 
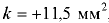, для ртути 
.
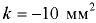Вследствие поверхностного натяжения жидкость, имеющая криволинейную поверхность, испытывает дополнительное давление
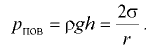
Высоту подъёма (или опускания) жидкости между параллельными стеклянными пластинами, расстояние между которыми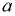 
(мм), можно определить по формуле
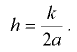
Вязкость — свойство жидкости оказывать сопротивление перемещению (сдвигу) одной его части относительно другой.
Если предположить, что поток состоит из отдельных слоев бесконечно малой толщины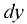 
(рис. 1.2), то скорости этих слоев будут изменяться по некоторому закону от нулевого значения у дна до максимального значения у поверхности. Пусть скорости соседних слоев равны 
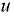и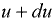 
.
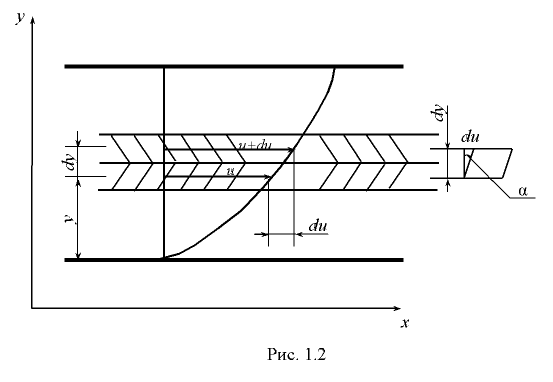
В прямолинейном движении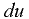 
можно рассматривать как скорость деформации, а приращение скорости 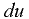, соответствующее приращению координаты 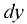(называемое градиентом скорости), как угловую скорость деформации 
.
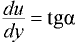Сила внутреннего трения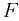 
, возникающая между двумя слоями движущейся прямолинейно жидкости, прямо пропорциональна площади поверхности 
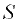соприкасающихся слоев, градиенту скорости 
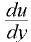, а также зависит от рода жидкости и температуры:
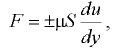
где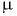 
— динамический коэффициент вязкости, зависящий от рода жидкости и температуры.
Касательное напряжение в жидкости
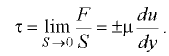
Так как 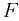и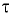 
всегда положительны, то выражения (1.16) и (1.17) имеют знак «плюс», если 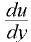положительно, и знак «минус», если 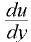отрицательно.
Динамический коэффициент вязкости численно равен касательному напряжению 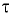при градиенте скорости 
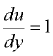, т.е. имеет вполне определенный физический смысл и полностью характеризует вязкость жидкости. Размерность 
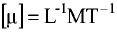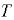( — обозначение времени). Единица динамического коэффициента вязкости в системе СИ — паскаль • секунда (Па • с). Также применяют таз (П):
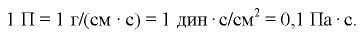
При выполнении технических расчётов в гидравлике используют кинематический коэффициент вязкости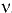 
, представляющий собой отношение динамического коэффициента вязкости жидкости 
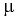к ее плотности :
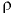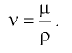
Размерность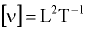 
. Единица кинематического коэффициента вязкости в системе СИ — 
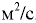. Также применяют стоке (Ст) и сантистокс (сСт):
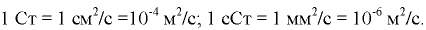
Значения динамического и кинематического коэффициентов вязкости приведены в прил. 1.
Для определения вязкости применяют приборы, называемые вискозиметрами. Вязкости жидкостей, более вязких, чем вода (масла, нефтепродукты и др.), определяют вискозиметром Энглера (рис. 1.3), состоящим из двух сосудов, пространство между которыми заполнено водой для поддержания требуемой температуры. В сферическом дне внутреннего сосуда 1 укреплена трубка 2 малого диаметра, выведенная через дно наружного сосуда 3. Отверстие в трубке в нормальном положении закрыто клапаном 4. Во внутренний сосуд до определённого уровня наливают испытываемую жидкость 5 и с помощью нагревательного устройства подогревают воду 6 в наружном сосуде.
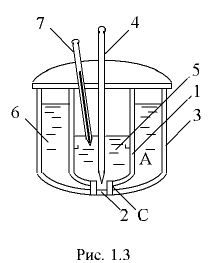
Повышение температуры воды вызывает повышение температуры испытываемой жидкости до требуемого значения температуры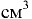 
, которое фиксируется термометром 7. После этого клапан открывают и с помощью мерной колбы и секундомера замеряют время истечения 200 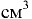испытываемой жидкости. Аналогичный опыт проводят с дистиллированной водой при температуре 
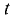= 20 °С. Отношение времени истечения испытываемой жидкости 
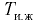к времени истечения дистиллированной воды 
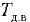В соответствует числу градусов условной вязкости (°ВУ) или градусов Энглера (°Е):
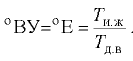
Пересчёт вязкости, выраженной в градусах Энглера, в единицы измерения СИ (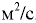) производится по формуле
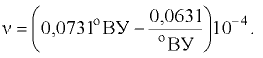
Вязкость зависит от рода жидкости, её температуры и давления (прил. 1). Для расчёта вязкости минеральных масел, применяемых в гидроприводах, в интервале значений температур от 30 до 150 С и вязкости до 10 ° ВУ пользуются зависимостью
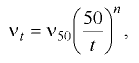
где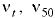 
— кинематический коэффициент вязкости масла соответственно при данной температуре 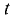и температуре 50 °С; 
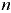— показатель степени, зависящий от вязкости масла, выраженной в °ВУ. при температуре 50 °С:
В интервале давления от 0 до 50 МПа вязкость минеральных масел, применяемых в гидроприводах, изменяется практически линейно и вычисляется по формуле
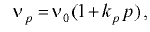
где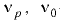 
— кинематические коэффициенты вязкости масла соответственно при давлении 
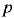(МПа) и атмосферном; 
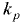— опытный коэффициент, зависящий от марки масла: для лёгких масел 
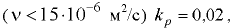, для тяжёлых 
.
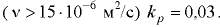Кинематический коэффициент вязкости воды в зависимости от температуры определяется по формуле
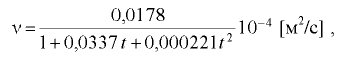
где 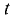— температура воды. °С.
Возможно эта страница вам будет полезна:
| Задачи по гидравлике |
Пример задачи №1.1.
Определить плотность жидкости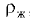 
, полученной смешиванием объёма жидкости 
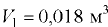(18 л) плотностью 
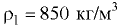и объёма жидкости 
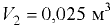(25 л) плотностью 
.
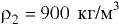Решение:
Плотность полученной жидкости находим из соотношения суммарных массы и объёма:
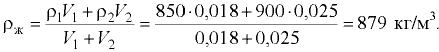
Давление в покоящейся жидкости
Общие сведения:
На жидкость действуют поверхностные и массовые силы. Поверхностные — это силы, действующие на поверхность жидкости, например силы давления поршня насоса или силы давления воздуха, газа. Массовые — это силы тяжести, инерции и центробежные силы, которые в однородной жидкости распределены по всему объему. При воздействии поверхностных и массовых сил в жидкости возникает давление.
Давлением в покоящейся жидкости называется напряжение сжатия [6]
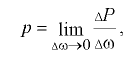
где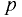 
— давление в точке; 
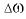— элементарная площадка, содержащая рассматриваемую точку; 
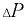— сжимающая сила, действующая на площадку .
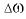Давление направлено по нормали к площадке, его величина не зависит от ориентации площадки в пространстве и является функцией координат точки жидкости.
Единица давления — паскаль (Па):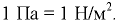 
. Более удобными для практического использования являются кратные единицы — килопаскаль (кПа) и мегапаскаль (МПа):
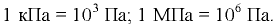
Наряду с этими (а также в обозначениях на приборах) используются и другие единицы давления:
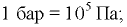
техническая атмосфера 1 ат =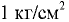
=98,1 кПа = 0,981 бар;
физическая атмосфера 1 атм = 760 мм рт. ст. = 101,4 кПа = 1,014 бар;
единицы высоты столба жидкости (мм рт. ст., м вод. ст.) 1 мм рт. ст. = 133,32 Па = 13,595 мм вод. ст.;
английская и американская системы единиц: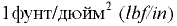 
= 6,89 кПа, 
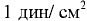= 0,1 Па.
При решении большинства технических задач с достаточной степенью точности можно принимать
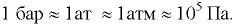
Давление, представляющее полное напряжение сжатия от действия всех внешних поверхностных и массовых сил, приложенных к жидкости, называется абсолютным давлением.
В технике отсчитывают давление от условного нуля, за который принято давление атмосферного воздуха на поверхности земли. Превышение (избыток) абсолютного давления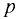 
над атмосферным 
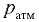называется избыточным давлением 
:
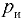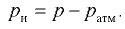
В технике широкое распространение получили манометры избыточного давления, которые измеряют превышение давления над атмосферным. Поэтому избыточное давление часто называют манометрическим.
Абсолютное давление может быть меньше атмосферного. Недостаток между абсолютным давлением и атмосферным называется вакуум метрическим давлением или вакуумом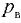 
:
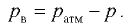
При абсолютном давлении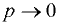 
вакуум метрическое 
.
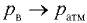Из выражений (2.2) и (2.3)
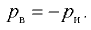
Таким образом, при абсолютном давлении, меньше атмосферного, избыточное давление отрицательно.
Атмосферное давление на поверхности жидкости. В однородной несжимаемой жидкости, находящейся под действием силы тяжести и атмосферного давления на свободной поверхности, давление определяется по закону
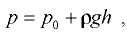
где 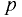— давление в произвольной точке жидкости на глубине 
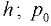— давление на свободной поверхности жидкости; 
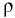— плотность жидкости; 
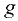— ускорение свободного падения.
Эта зависимость представляет основной закон равновесия жидкости в однородном поле тяжести. В рассматриваемом случае равновесия жидкости горизонтальные плоскости являются поверхностями равного давления.
На рис. 2.1 показаны эпюры давления жидкости на боковые стенки сосуда. Слева построена эпюра давления, отвечающая избыточному давлению, справа — абсолютному давлению.
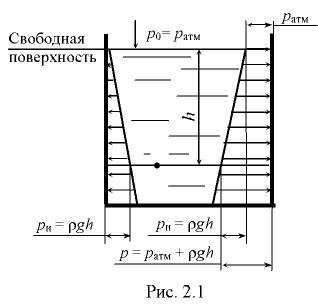
При определении давления в точках жидкости, заполняющей открытый в атмосферу сосуд, известно поверхность действующее на жидкость внешнее давление, равное атмосферному. При этом абсолютное давление в произвольной точке жидкости на глубине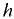 
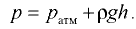
Избыточное давление, создаваемое в данном случае только весом жидкости,
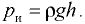
В ирил. 2 приведено изменение атмосферного давления в зависимости от высоты над уровнем моря.
Избыточное давление на поверхности жидкости. Если в закрытом сосуде на поверхность жидкости действует избыточное давление, т.е. внешнее давление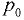 
, которое больше окружающего атмосферного давления 
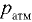, то пьезометрическая плоскость, отвечающая атмосферному давлению, располагается над свободной поверхностью жидкости на высоте
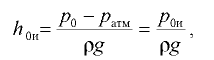
где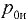 
— избыточное давление па поверхности жидкости.
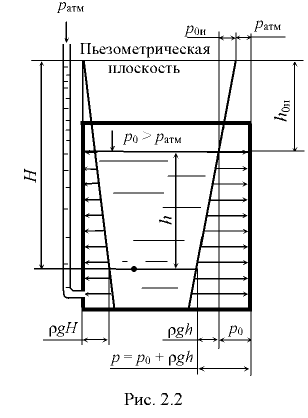
Формулы (2.7) и (2.8) дают возможность выражать избыточное давление в любой точке жидкости через пьезометрическую высоту, т.е. величину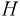 
заглубления данной точки под пьезометрической плоскостью — плоскостью атмосферного давления.
Эта плоскость проходит через уровень в пьезометре, присоединенном к сосуду (рис. 2.2).
Так, для воды в открытом водоеме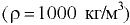 
на глубине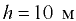 
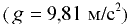избыточное давление 
.
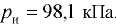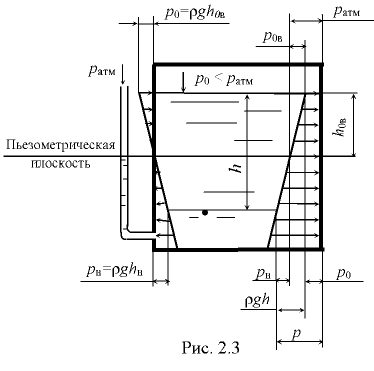
Вакуумметрическое давление на поверхности жидкости. Если в закрытом сосуде на поверхность жидкости действует вакуумметрическое давление, т.е. внешнее давление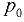 
, которое меньше окружающего атмосферного давления 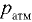, то пьезометрическая плоскость находиться под поверхностью жидкости на высоте
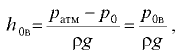
где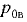 
— вакуумметрическое давление на поверхности жидкости (рис. 2.3).
Величину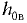 
называют вакуумметрической высотой.
При измерении невысоких давлений (меньше одной атмосферы) используются жидкостные манометры различных конструкций. На рис. 2.4 показан дифференциальный жидкостный манометр, при помощи которого измеряют разность давления в двух резервуарах, расположенных на разной высоте и заполненных различными жидкостями.
Расчетные зависимости давления от высот столбов жидкости получают из уравнений равновесия жидкостей. Для их составления целесообразно выбрать плоскость сравнения 0-0, от которой ведется отсчет давления. Плоскость сравнения целесообразно проводить через нижнюю точку колена манометра или через линию раздела жидкостей, как показано на рис. 2.4.
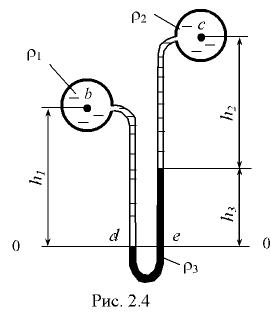
В этом случае давление в точках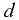 
и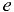 
будет одинаково: 
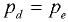. Давление в точке 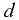относительно давления в точке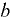 
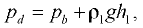
где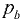 
— давление в точке 
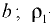— плотность жидкости в резервуаре ; 
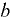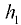— высота столба жидкости плотностью 
.
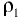Давление в точке 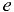относительно давления в точке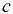 
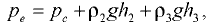
где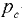 
— давление в точке 
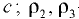— плотность жидкости соответственно в резервуаре 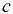и колене манометра; 
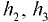— высота столба жидкости соответственно плотностью 
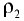и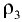 
Тогда уравнение равновесия примет вид
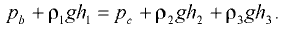
При решении задач используют уравнение равновесия, из которого выражают неизвестную величину.
Возможно эта страница вам будет полезна:
| Решение задач по гидравлике |
Пример задачи №2.1.
На какой высоте 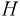установится вода в трубке, первоначально заполненной водой, а потом опрокинутой и погруженной открытым концом под уровень воды, если атмосферное давление составляет 98 кПа. Температура воды 20 °С, плотность воды 
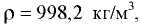давление насыщенных паров воды 
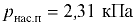(рис. 2.5).
Решение:
Вода находится в равновесии. Наметим поверхность равного давления. Это может быть любая горизонтальная плоскость, проходящая на глубине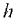 
. На этой плоскости рассмотрим две точки — 1 и 2.
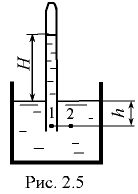
Абсолютное давление в т. 1
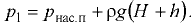
Абсолютное давление в т. 2
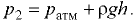
Точки лежат на поверхности равного давления, тогда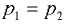 
или
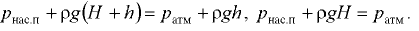
Очевидно, что полученное выражение справедливо для плоскости равного давления, совпадающей со свободной поверхностью жидкости в сосуде. Отсюда
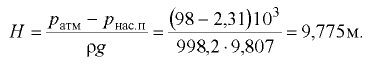
Силы давления покоящейся жидкости на плоские стенки
Общие сведения:
Полная сила давления жидкости на плоскую стенку равна сумме сил внешнего давления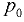 
и избыточного давления, создаваемого весом жидкости, 
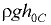[6]:
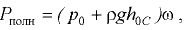
где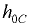 
— расстояние по вертикали от центра тяжести площади 
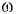до свободной поверхности жидкости (рис. 3.1).
Единицей силы давления является ньютон (Н). Более удобными для практического использования являются кратные единицы — килоньютон (кН) и меганьютон (МН):
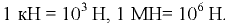
В технике определяют силы избыточного давления жидкости на плоскую стенку
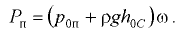
В большинстве случаев требуется определить результирующую силу давления.
Если на одну сторону плоской стенки оказывает давление жидкость, а на другую (несмоченную) — атмосферное давление, то результирующая сил давления, нормальная к ней, опрерделяется по формуле (3.2), которую можно преобразовать следующим образом (рис. 3.1)
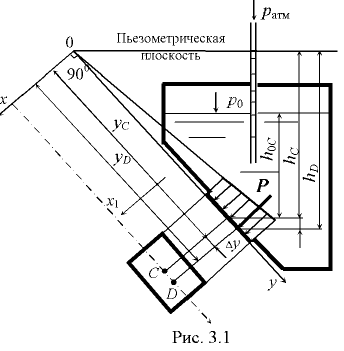
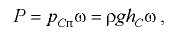
где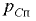 
— избыточное давление в цент ре тяжести площади ,
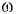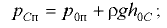
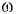— смоченная площадь стенки; 
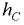— расстояние по вертикали от центра тяжести площади 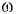до пьезометрической плоскости.
При избыточном давлении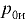 
на свободную поверхность пьезометрическая плоскость проходит над свободной поверхностью жидкости на расстоянии 
.
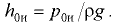Если 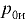= 0, то пьезометрическая плоскость совпадает со свободной поверхностью и нагрузка на стенку создаётся только давлением жидкости.
Центр давления — точка пересечения линии действия силы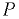 
с плоскостью стенки. Положение центра давления (точка 
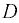) в плоскости стенки определяется по формулам
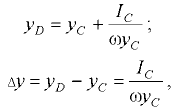
где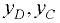 
— расстояния от центра давления 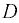и центра тяжести 
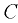площади стенки до линии пересечения с пьезометрической плоскостью; 
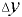— смещение центра давления относительно центра тяжести вдоль оси 
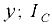— момент инерции площади стенки относительно горизонтальной оси 
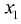, проходящей через центр тяжести площади стенки.
Формулу (3.4) можно привести к виду
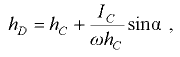
где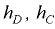 
— вертикальные расстояния соответственно от центра давления 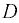и центра тяжести 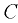площади стенки до пьезометрической плоскости: 
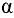— угол наклона стенки к горизонту.
Для вертикальной стенки (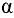 = 90°)
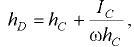
смещение центра давления
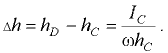
Для горизонтальной стенки (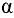 = 0) имеем 
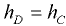(центр давления и центр тяжести совпадают).
В прил. 3 даны моменты инерции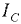 
площадей некоторых плоских симметричных фигур и координаты их центров тяжести.
Приведенные выше зависимости справедливы при любом избыточном давлении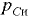 
в центре тяжести 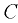площади стенки, в том числе и при отрицательном избыточном давлении, т.е. когда в точке 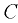вакуум метрическое давление. В этом случае пьезометрическая плоскость проходит ниже центра тяжести стенки (рис. 3.2) и расстояния 
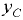и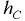 
становятся отрицательными. При этом центр давления 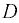расположен выше центра тяжести 
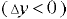а результирующая сила, воспринимаемая стенкой, направлена внутрь жидкости. На рис. 3.2 
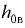— вакуумметрическая высота, 
.
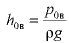При воздействии жидкостей на плоскую стенку с двух сторон следует сначала определить силы давления на каждую сторону стенки, а затем найти их результирующую по правилам сложения параллельных сил (рис. 3.3):
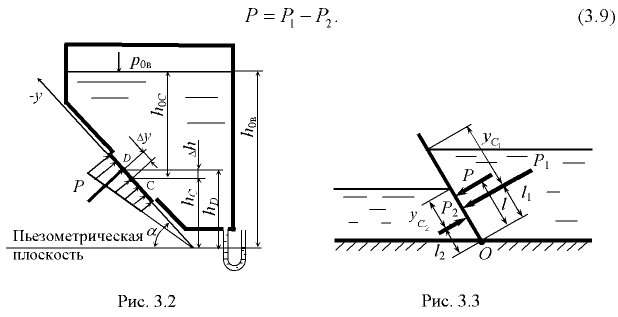
Центр давления результирующей силы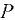 
определяется из уравнения моментов сил относительно точки 
:
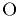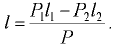
Если плотности жидкостей одинаковы, то в некоторых случаях результирующую силу давления на стенку удобно найти по суммарной эпюре нагрузки, интенсивность которой равна разности давлений, действующих по обе стороны стенки в каждой точке ее поверхности.
На рис. 3.4 показано определение силы давления с помощью такой эпюры в случае двустороннего воздействия жидкостей одинаковой плотности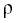 
на стенку при различных уровнях 
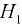и 
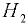по обе стороны стенки и одинаковом давлении на свободные плоскости I и II.
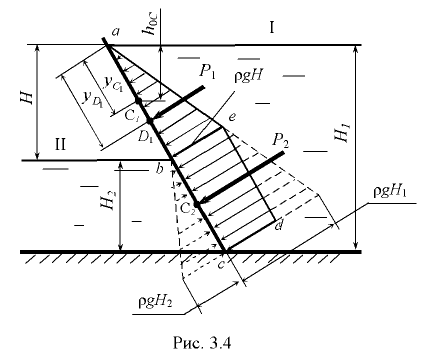
Для верхнего участка стенки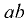 
, подверженного одностороннему давлению жидкости (эпюра нагрузки в плоскости чертежа представляет треугольник 
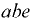), сила давления 
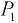определяется по формуле (3.3):
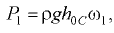
где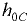 
— вертикальное расстояние от центра тяжести 
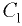верхнего участка стенки до свободной поверхности 
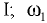— площадь этого участка.
Координата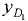 
центра давления участка 
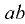определяется по формуле (3.4).
На нижнем участке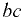 
разность давлений по обе стороны стенки постоянная. Это следует из эпюр давления на каждую сторону стенки (треугольники с основаниям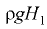и 
и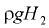 
). Суммарная эпюра нагрузки для участка 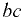представляет в плоскости чертежа прямоугольник 
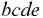с высотой 
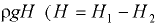— разность уровней жидкости).
Сила давления, воспринимаемая нижним участком,
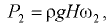
где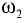 
— площадь нижнего участка стенки.
Сила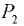 
проходит через центр тяжести 
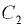площади .
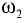Результирующая сила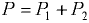 
, линия ее действия де;гит отрезок между точкам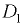и 
и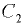 
на части, обратно пропорциональные силам 
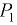и .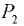
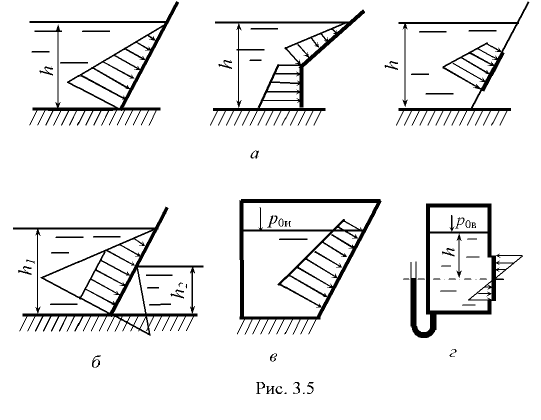
На рис. 3.5 показаны примеры построения эпюр давления на плоские стенки: а — при атмосферном давлении; б — двустороннем давлении жидкости; в — избыточном давлении; г — вакуумметрическом давлении.
Возможно эта страница вам будет полезна:
| Методические указания по гидравлике |
Пример задачи №3.1.
Определить силу давления на вертикальную прямоугольную перегородку закрытого резервуара высотой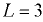 
м и шириной 
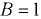м, по обе стороны которой различны как уровни воды, так и давления газа.
Исходные данные:
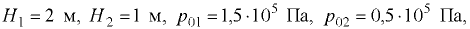
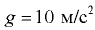
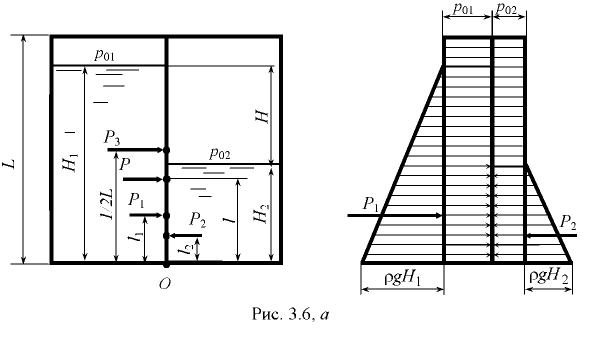
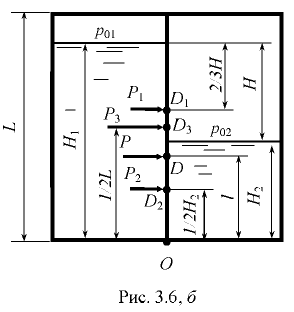
(рис. 3.6, а, б).
Решение:
Первый вариант. Силу давления, создаваемую весом воды, на перегородку приведем к двум силам (рис. 3.6, а): силе, действующей на перегородку слева,
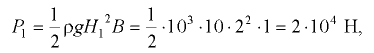
действующей на перегородку справа,
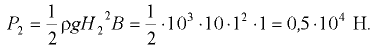
Силы 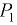и 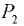приложены в точках, расположенных на расстояниях соответственно 
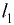и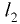 
от дна резервуара:
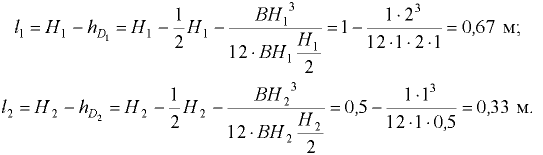
Сила двустороннего давления газа на перегородку
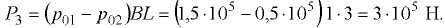
Линия действия силы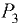 
проходит по середине высоты перегородки 
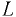. Результирующая сила, воспринимаемая перегородкой,
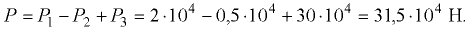
Уравнение суммы моментов сил, действующих на перегородку, относительно точки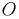 
имеет вид
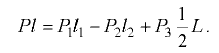
Отсюда
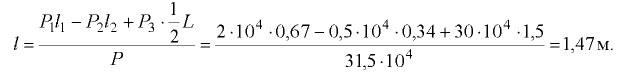
Второй вариант. Давление жидкости на перегородку приведем к двум силам 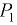и 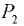(рис. 3.6, б). Силу 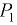на участке одностороннего давления определим по формуле (3.3):
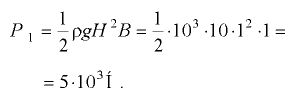
Координату центра давления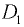 
найдем по формуле (3.7), в которой
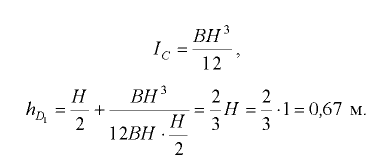
Силу 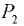на участке двустороннего давления жидкости определим по формуле (3.11), в которой 
:
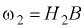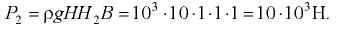
Линия действия силы 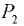проходит по середине высоты 
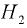. Сила двустороннего давления газа
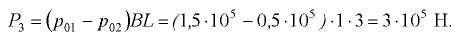
Линия действия силы 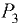проходит по середине высоты перегородки 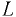. Результирующая сила, воспринимаемая перегородкой,
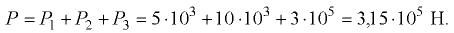
Уравнение суммы моментов сил, действующих на перегородку, относительно точки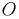
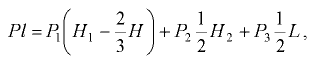
где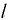 
— координата центра давления 
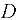результирующей силы относительно точки .
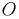Отсюда
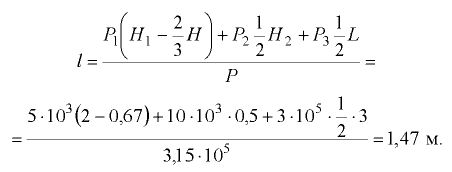
Силы давления покоящейся жидкости на криволинейные поверхности (стенки)
Общие сведения:
Распределенная нагрузка, действующая на криволинейную поверхность от нормальных в каждой её точке сил давления жидкости, может быть приведена к равнодействующей силе [6]. В большинстве практических задач рассматриваются криволинейные стенки, симметрично расположенные относительно вертикальной плоскости. В этом случае равнодействующая сила лежит в плоскости симметрии. Величина и направление равнодействующей силы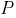 
определяются по двум составляющим, обычно горизонтальной и вертикальной (рис. 4.1).
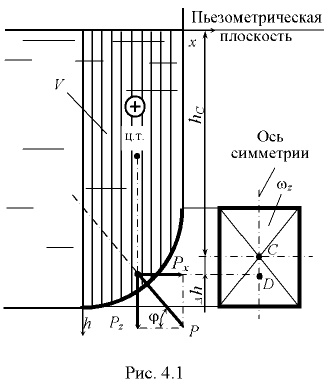
Горизонтальная составляющая силы давления, воспринимаемая криволинейной стенкой, равна силе давления на вертикальную проекцию этой стенки, нормальную к плоскости симметрии, и определяется по формуле
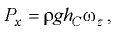
где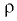 
— плотность жидкости; 
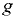— ускорение свободного падения: 
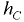— вертикальное расстояние от центра тяжести вертикальной проекции стенки (точка 
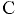) до пьезометрической плоскости; 
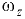— площадь вертикальной проекции стенки.
При избыточном давлении в точке 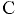пьезометрическая плоскость проходит выше этой точки и 
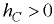, при вакуумметрическом давлении в точке 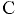, т.е. при отрицательном избыточном, пьезометрическая плоскость проходит ниже этой точки и 
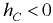. Положительные направления координатных осей показаны на рис. 4.1.
Линия действия силы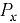 
лежит в плоскости симметрии, проходит через центр давления вертикальной проекции стенки (точка 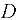) и смещена (вниз, если 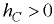, или вверх, если 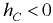) относительно центра тяжести вертикальной проекции на расстояние
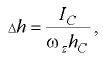
где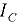 
— момент инерции площади вертикальной проекции относительно горизонтальной оси, проходящей через центр тяжести проекции.
Вертикальная составляющая силы давления, воспринимаемая криволинейной стенкой, равна силе тяжести жидкости в объёме тела давления:
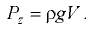
Тело давления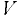 
ограничено криволинейной поверхностью, пьезометрической плоскостью и вертикальной проецирующей поверхностью, построенной на контуре стенки. Объем тела давления находят геометрически. При необходимости сложное тело давления можно разбить на элементарные и просуммировать их объемы. Объемы тел приведены в прил. 4.
Сила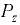 
проходит через центр тяжести объёма 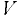и направлена вниз, если объём определяется со смоченной стороны стенки, и вверх — если объём определяется с несмоченной стороны стенки.
Полная равнодействующая сила давления жидкости на криволинейную стенку равна геометрической сумме сил 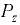и 
:
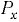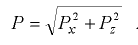
Линия действия силы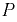 
проходит через точку пересечения линий действия сил 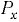и .
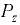Угол наклона равнодействующей к горизонту
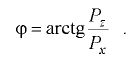
Для стенок постоянного радиуса кривизны (цилиндрических, сферических) равнодействующая сила давления проходит через ось или центр кривизны стенки. На рис. 4.2 показаны примеры построения тел давления в случаях, если сила давления жидкости действует на криволинейную стенку с одной или двух сторон. Тело давления, которое лежит в области действительной жидкости, считают положительньм, а тело давления в области воображаемой жидкости — отрицательным.
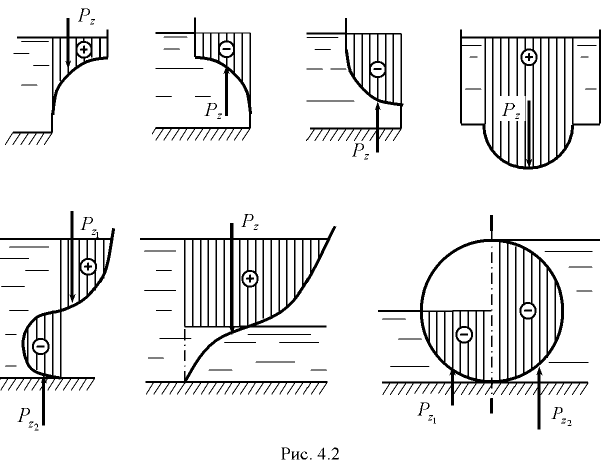
При избыточном давлении на смоченной стороне стенки все составляющие и равнодействующая направлены изнутри жидкости на стенку, а в случае вакуумметрического давления на смоченной стороне стенки силы направлены от стенки внутрь жидкости.
При воздействии жидкостей на стенку с двух сторон сначала определяют горизонтальные и вертикальные составляющие с каждой стороны стенки в предположении одностороннего воздействия жидкости, а затем горизонтальные и вертикальные составляющие от воздействия с двух сторон.
На рис. 4.3 показано определение горизонтальной и вертикальной составляющих и полной силы давления жидкости на криволинейную стенку при избыточном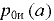 
и вакуумметрическом 
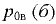давлении.
Вакуум метрическая высота
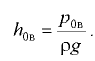
В некоторых случаях для нахождения той или иной составляющей силы давления жидкости на стенку следует разбить её поверхность на отдельные участки, определить соответствующие усилия на каждый участок стенки и далее просуммировать их.
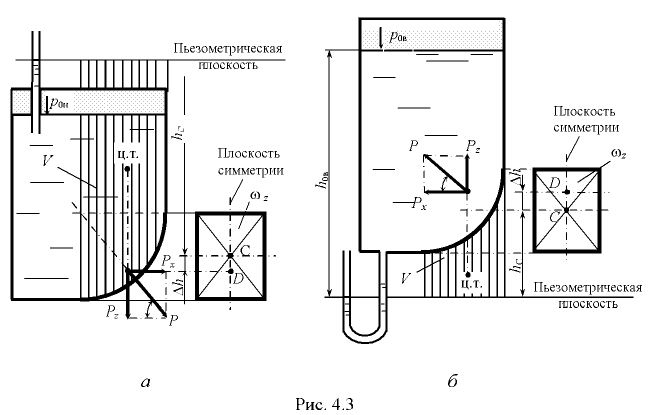
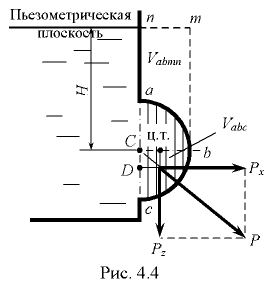
Так, для определения вертикальной составляющей силы давления жидкости на цилиндрическую поверхность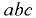 
(рис. 4.4) следует разбить рассматриваемую поверхность горизонтальной плоскостью на верхнюю 
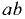и нижнюю 
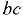половины и найти вертикальные силы давления жидкости на каждую из них.
Вертикальная сила на стенку 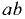равна весу жидкости в объёме 
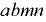и направлена вверх; вертикальная сила на стенку 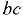равна весу жидкости в объёме 
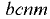и направлена вниз. Тогда вертикальная сила давления на всю цилиндрическую поверхность равна разности указанных сил:
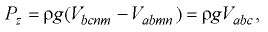
т.е. равна весу жидкости в объёме половины цилиндра и направлена вниз.
Горизонтальная сила в рассматриваемом случае определяется на всю цилиндрическую поверхность по формуле (4.1), а полная — по формуле (4.4).
В том случае, когда криволинейную стенку пересекает пьезометрическая плоскость, вертикальную составляющую силы давления жидкости также следует определять как сумму сил, действующих на участки стенки. Следует иметь в виду, что на участок стенки, находящийся выше пьезометрической плоскости, действует вакуумметрическое давление, а на участок стенки ниже пьезометрической плоскости — избыточное.
Пример задачи №4.1.
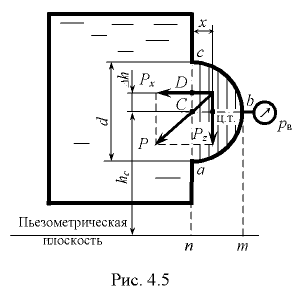
На боковой поверхности резервуара, заполненного водой, имеется полусферическая крышка диаметром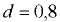 
м (рис. 4.5). Определить горизонтальную и вертикальную составляющие сил давления жидкости на крышку при показании вакуумметра 
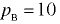кПа.
Решение:
Находим положение пьезометрической плоскости, вертикальное расстояние от которой до центра тяжести (точка 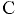) вертикальной проекции полусферической крышки 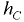равно вакуум метрической высоте. В технике избыточное давление и соответствующая ему пьезометрическая высота, измеряемая от пьезометрической плоскости, приняты положительными, а вакуумметрическое давление и вакуум метрическая высота — отрицательными.
Тогда
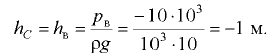
Горизонтальная составляющая давления жидкости на полусферическую крышку
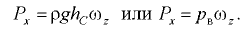
‘Гак как площадь вертикальной проекции крышки есть круг диаметром 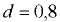м, то
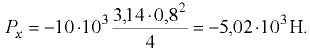
Знак «минус» показывает, что на крышку действует сила внешнего давления, которая направлена внутрь жидкости.
Центр давления силы 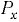(точка 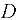на вертикальной проекции крышки) смещен вверх на
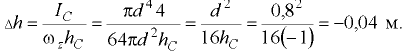
Вертикальная составляющая силы гидростатического давления на верхнюю четверть сферической крышки направлена вниз
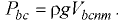
Вертикальная составляющая давления на нижнюю четверть сферической крышки направлена вверх
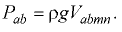
Следовательно, вертикальная составляющая на всю полусферическую крышку
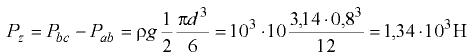
и направлена вниз.
Линия действия силы 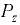проходит через центр тяжести объёма тела давления (объёма полусферы), т.е. на расстоянии 
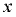от центра кривизны полусферы. Равнодействующая сила 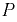проходит через центр кривизны. Следовательно, расстояние 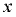от центра кривизны полусферы до линии действия силы 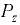можно найти из соотношения
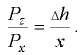
Отсюда
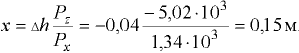
Плавание тел. остойчивость
Общие сведения:
На тело, погруженное в жидкость, действует выталкивающая сила, направленная вертикально вверх и равная весу жидкости в объёме 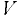, вытесненном телом:
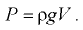
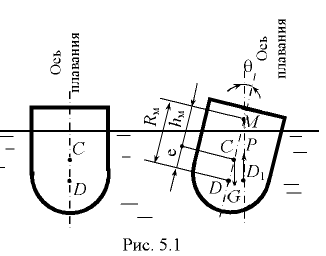
Эта сила является результирующей сил давления жидкости на погруженное в неё тело. Она проходит через центр тяжести вытесненного объёма жидкости, который называется центром водоизмещения (на рис. 5.1 точка ).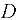
Соотношение между весом тела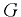 
и выталкивающей силой 
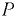определяет три условия плавания:
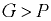— тело тонет;
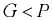— тело всплывает;
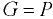— тело плавает, причем тело плавает на свободной поверхности жидкости при частичном погружении его в жидкость и в подводном состоянии при полном погружении.
Вес тела можно найти через плотность материала тела и ег о объем. Средние значения плотности наиболее распространенных материалов приведены в прил. 5.
При равновесии плавающего на свободной поверхности тела его центр тяжести (точка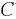 
) находится на общей вертикали, которая называется осью плавания. Ось плавания перпендикулярна к свободной поверхности воды (плоскости плавания).
При наклоне (крене) плавающего тела центр водоизмещения изменяет положение (точка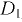 
) ось плавания наклонена к вертикали под углом крена 
.
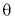Точку пересечения выхаживающей силы 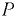при крене тела с осью плавания (точка 
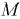) принято называть метацентром. Расстояние между центром тяжести 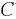и метацентром 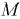называется метацеитрической высотой 
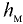, а расстояние между центром водоизмещения 
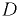и метацентром 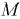— мета-центрическим радиусом 
.
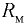Чем выше расположен метацентр над центром тяжести тела, т.е. чем больше метацентрическая высота, тем больше остойчивость тела (способность из крена переходить в положение равновесия), так как момент остойчивости прямо пропорционален метацентрической высоте:
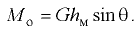
При малых углах крена метацентричеекую высоту можно определить но формуле
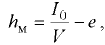
где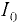 
— момент инерции площади плоскости плавания относительно её продольной оси симметрии, образованной при пересечении плоскости плавания диаметральной (диаметральная плоскость — это вертикальная продольная плоскость, которая делит плавающее на поверхности тело на две симметричные части); 
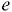— эксцентриситет (расстояние между центром тяжести и центром водоизмещения).
Формулу (5.3) можно записать так:
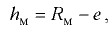
где 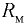— метацентрический радиус,
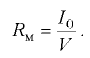
Таким образом, положение тела при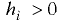 
— остойчивое, 
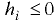— неостойчивое.
Пример задачи №5.1.
Погруженный в воду полый шаровой клапан диаметром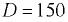 
мм и массой 
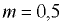кг закрывает входное отверстие грубы с внутренним диаметром 
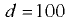мм (рис. 5.2). При какой разности уровней 
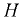клапан начнёт пропускать воду из трубы в резервуар?
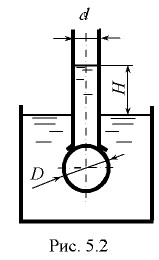
Решение:
На шаровой клапан действует выталкивающая сила, которая является результирующей сил давления жидкости и направлена вверх:
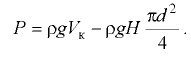
В данном выражении первое слагаемое является результирующей сил давления жидкости на клапан при условии 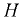= 0. Эта сила направлена вверх. В этом слагаемом 
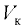— объём шарового клапана:
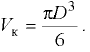
Второе слагаемое — это сила давления столба жидкости высотой 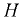, она направлена вниз.
Клапан начнет пропускать воду, когда вес клапана уравновешивается силой :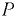
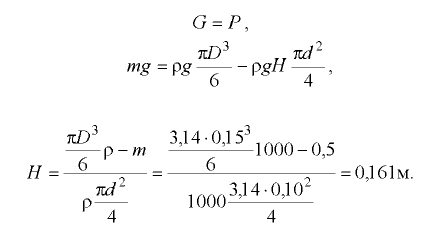
Равновесие жидкости в движущихся сосудах
Общие сведения:
При равновесии в движущемся сосуде жидкость, заполняющая сосуд, движется вместе с ним как твердое тело. В зависимости от характера действующих массовых сил в жидкости поверхность равного давления, как и свободная поверхность, может принимать различную форму. Рассмотрим некоторые случаи равновесия жидкости в движущихся сосудах.
- Жидкость находится в сосуде, который движется прямолинейно в горизонтальном направлении с постоянным ускорением
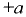(рис. 6.1, а) или с постоянным замедлением 
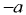(рис. 6.1, б).
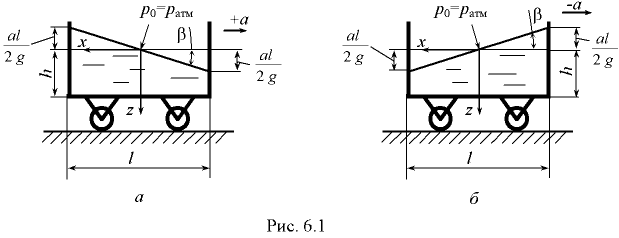
В данном случае жидкость подвержена воздействию не только поверхностных сил, но также массовых сил тяжести и инерции.
Поверхность равного давления является наклонной плоскостью. Давление в любой точке жидкости определяется по формуле [1 ]
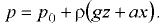
Для свободной поверхности жидкости, когда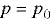 
, уравнение имеет вид
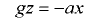
или
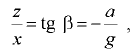
где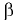 
— угол наклона свободной поверхности жидкости к горизонту.
Для жидкости, заполняющей сосуд, открытый в атмосферу, т.е. при условии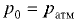 
избыточное давление в любой точке жидкости определяется по формуле
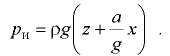
Формула (6.4) применима и для замкнутых сосудов с избыточным давлением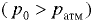 
над жидкостью, если отсчитывать координаты 
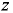и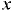 
от пьезометрической плоскости, т.е. от поверхности уровня, давление в точках которой равно атмосферному (рис. 6.2). Так, при определении давления в точке 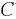формула (6.4) примет вид
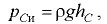
где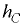 
— расстояние от точки 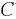до пьезометрической плоскости.
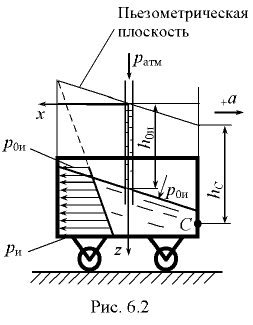
В формуле (6.4) величина есть глубина погружения по вертикали от пьезометрической плоскости до точки, в которой определяется давление.
Если сосуд движется равномерно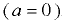 
, уравнение (6.1) примет вид
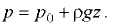
Силы давления жидкости на плоские стенки в рассматриваемом случае равновесия, благодаря однородности поля массовых сил, определяются зависимостями, которые используются в случае равновесия жидкости в неподвижном сосуде [2]. Координаты центра давления действующих сил зависят от величины и направления ускорения а и определяются по формулам, приведенным в [2].
- Жидкость находится в сосуде, который движется прямолинейно с углом наклона к горизонту а и с постоянным ускорением 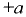(рис. 6.3, а) или с постоянным замедлением 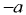(рис. 6.3, б).
Давление в любой точке жидкости определяется по формуле
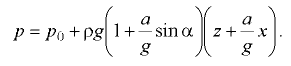
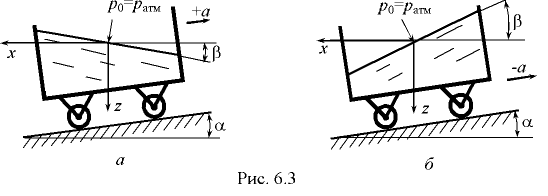
В формуле (6.5) величина
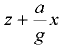
есть глубина погружения по вертикали от пьезометрической плоскости до точки, в которой определяется давление, а угол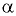 
принимается со знаком «плюс» при движении сосуда на подъёме и со знаком «минус» на спуске.
Если сосуд движется вертикально вверх (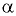 = 90°), то уравнение (6.5) принимает вид
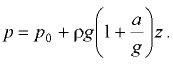
Если сосуд движется вертикально вниз (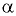 = -90°), то
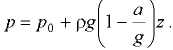
В выражениях (6.1)-(67) ускорение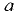 
принимается с учетом знака.
Изложенные выше замечания к формуле (6.4) справедливы и для формул (6.5)-(6.7). Также справедливы в данном случае и замечания по определению сил давления жидкости на плоские стенки и координат центра давления.
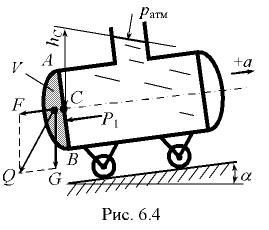
Силу давления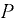 
на криволинейную стенку можно определить также из условия относительного равновесия жидкости объемом 
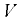, заключенной между криволинейной стенкой и плоским сечением, проведенным через граничный контур стенки (рис. 6.4):
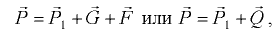
где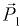 
— сила давления на плоское сечение 
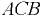, проведенное через граничный контур
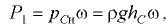
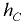— расстояние по вертикали от пьезометрической плоскости до центра тяжести сечения 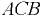(точка ); 
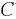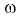— площадь сечения 
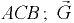— вес жидкости объемом ,
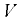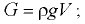
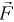— сила инерции жидкости, заключенной в объеме ,
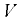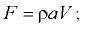
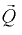— суммарная массовая сила,
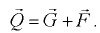
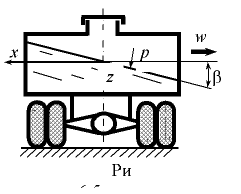
- Жидкость находится в сосуде, который движется но горизонтальному закруглению с постоянной скоростью (рис. 6.5). В данном случае на жидкость действуют поверхностные силы, массовые силы тяжести и инерции. Поверхность равного давления является наклонной плоскостью. Давление в любой точке жидкости определяется по формуле
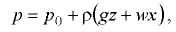
где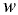 
— центробежное ускорение; при условии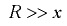 
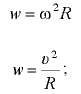
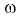— угловая скорость движения сосуда: 
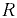— радиус закругления; 
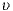— линейная скорость движения сосуда.
Для свободной поверхности жидкости, когда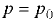 
, уравнение (6.13) принимает вид
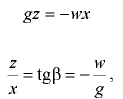
где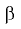 
— угол наклона свободной поверхности жидкости к горизонту.
При условии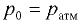 
избыточное давление в любой точке жидкости определяется по формуле
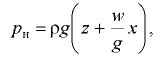
где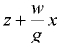 
— глубина погружения по вертикали от пьезометрической плоскости до точки, в которой определяется давление 
.
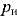Формула (6.18) применима и для сосудов с избыточным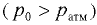 
или вакуумметрическим давлением 
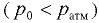над жидкостью, если отсчитывать координаты 
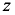и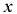 
от пьезометрической плоскости, т.е. от поверхности уровня, давление в точках которого равно атмосферному.
- Жидкость находится в сосуде, равномерно вращающемся относительно вертикальной оси. В этом случае жидкость подвержена воздействию поверхностных сил, массовых сил тяжести и инерции. Причем поле центробежных сил инерции неоднородно, так как центробежные силы, действующие на жидкость, зависят от центробежного ускорения
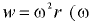— угловая скорость сосуда), а ускорение зависит от радиуса 
.
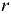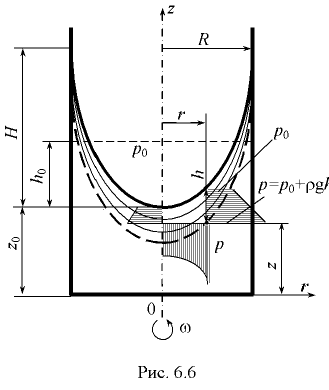
Поверхность уровня представляет собой параболоид вращения, ось которого совпадает с осью вращения сосуда (рис. 6.6).
Уравнение поверхности уровня во вращающихся вместе с сосудом цилиндрических координатах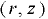 
имеет вид
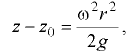
где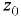 
— вертикальная координата вершины параболоиды поверхности уровня; 
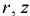— координаты любой точки поверхности уровня.
Высота параболоида
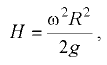
где 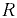— радиус сосуда. Закон распределения давления в жидкости выражается уравнением
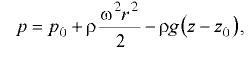
где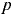 
— давление в произвольной точке жидкости с координатами 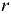и 
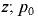— давление в точках параболоида поверхности уровня, вертикальная координата вершины которого равна .
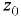Из уравнения следует, что в любой точке на глубине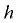 
от поверхности уровня с давлением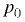 
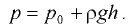
Избыточное давление в точках на глубине 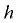под параболоидом пьезометрической поверхности (в открытом сосуде — под параболоидом свободной поверхности)
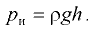
Из уравнения (6.20) следует параболический закон распределения давления по радиусу (рис. 6.6).
Если обозначить расстояние между первоначальным уровнем жидкости (до вращения сосуда) и вершиной параболоида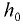 
(рис. 6.6), то 
.
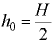Положение свободной поверхности жидкости в сосуде определяется объемом находящейся в нем жидкости. При этом объем параболоида вращения
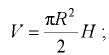
объем жидкости во вращающемся цилиндрическом сосуде в случае, когда свободная поверхность жидкости пересекает дно сосуда (рис. 6.7),
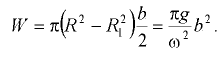
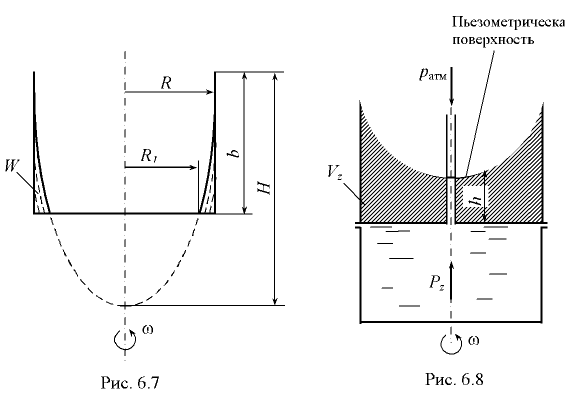
Когда свободная поверхность отсутствует, положение пьезометрической поверхности определяется из условия, что она проходит через точку жидкости, давление в которой равно атмосферному. На рис. 6.8 заштрихована площадь сечения тела давления на верхнюю крышку сосуда вертикальной плоскостью, проходящей через ось вращения. Сила давления жидкости на вертикальную крышку
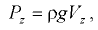
где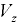 
— объем тела давления, построенного параллельно направлению 
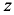, между стенкой и пьезометрической поверхностью.
- Жидкость находится в сосуде, равномерно вращающемся вокруг горизонтальной оси. В данном случае жидкость также подвержена воздействию массовых сил тяжести и центробежной силы. Поверхности равного давления представляют концентрически расположенные боковые поверхности цилиндров, оси которых горизонтальны и смещены относительно оси
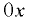на величину эксцентриситета 
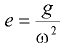(рис. 6.9, а).
Рассмотрим случай, когда центробежные силы велики по сравнению с силой тяжести жидкости и последней можно в расчетах пренебречь, т.е. при условии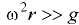 
.
При данном условии поверхности уровня представляют собой концентричные цилиндры с осями, совпадающими с осью вращения сосуда (рис. 6.9, б). Закон распределения давления для этог о случая имеет вид
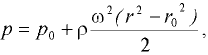
где 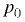— давление в точках цилиндрической поверхности радиусом 
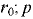— давление в точках цилиндрической поверхности радиусом 
.
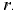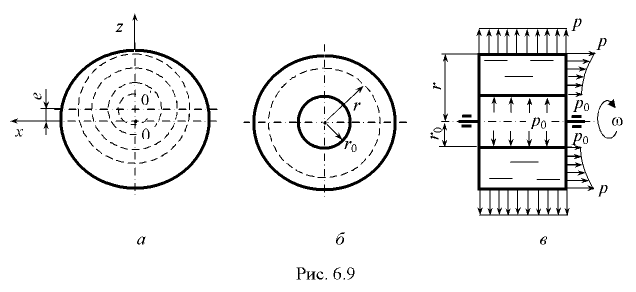
Закон распределения давления (6.26) по радиусу является параболическим. Эпюры давления представлены на рис. 6.9, в. Если сила тяжести мала по сравнению с центробежной, то формула (6.26) может применяться при любом расположении оси вращения сосуда.
Пример задачи №6.1.
Цистерна диаметром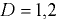 
м и длиной 
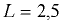м, наполненная нефтью (относительная плотность 
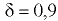) до высоты 
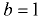м, движется горизонтально с постоянным ускорением 
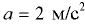(рис. 6.10). Определить силы давления на плоские торцовые крышк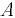и 
и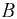 
цистерны. Ускорение свободного падения 
.
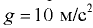Решение:
При горизонтальном движении сосуда с ускорением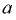 
свободная поверхность жидкости наклонится к горизонту под углом 
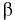, определяемым из условия
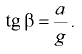
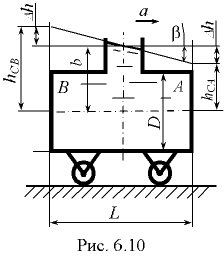
Вычислим величину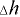 
, на которую опустится нефть у передней стенки 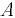и поднимется у задней стенки :
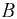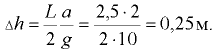
Сила давления нефти на крышку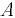
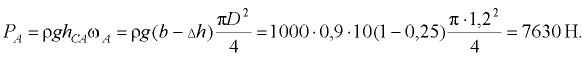
Сила давления нефти на крышку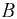
Режимы движения жидкости
Общие сведения:
Потоком жидкости называется движущаяся масса жидкости, ограниченная твердыми направляющими поверхностями, поверхностями раздела жидкостей и свободной поверхностью.
Все возможные виды движения жидкости подразделяют на две категории:
- безвихревое (потенциальное) — когда вращение элементарных частиц жидкости отсутствует;
- вихревое — когда присутствует вращение элементарных частиц жидкости и им пренебречь нельзя.
В зависимости от движения жидкости по времени различают:
- неустановившееся (нестационарное) движение — когда скорость
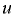в выбранной точке пространства зависит от координат 
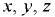и изменяется с течением времени 
:
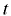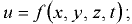
- установившееся (стационарное) движение — когда скорость 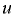не изменяется с течением времени и зависит только от координат выбранной точки
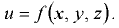
В зависимости от геометрической формы линий тока и характера изменения поля скоростей различают потоки:
- с равномерным движением, характеризующимся параллельностью и прямолинейностью линий тока;
- с неравномерным движением, когда линии тока не являются параллельными прямыми, а площади живых сечений и средние скорости -переменные по длине потока.
Также потоки могут иметь:
а) плавно изменяющееся движение (угол расхождения между линиями тока или их кривизна малы, живые сечения принимаются плоскими);
б) резко изменяющееся движение (угол расхождения между линиями тока или их кривизна велики, живые сечения криволинейны).
В зависимости от характера границ потоки делятся на:
- напорные — со всех боковых сторон ограничены твердыми стенками;
- безнапорные — частично ограничены твердыми стенками и частотно свободной поверхностью;
- гидравлические струи — ограничены только жидкостью или газовой средой, твердых границ не имеют.
Наряду с приведенными существуют и другие классификации потоков жидкости.
Траекторией называется линия, которую описывает частица жидкости при своем движении.
Линией тока называется кривая, в каждой точке которой в данный момент времени векторы скорости являются касательными к ней. В случае установившегося движения траектории и линии тока совпадают и неизменны во времени.
Трубкой тока называется совокупность линий тока, проведенных через каждую точку бесконечно малого контура.
Элементарной струйкой называется семейство (пучок) линий тока, проходящих через все точки бесконечно малой площадки с/со, которая перпендикулярна направлению движения (рис. 7.1). Элементарной струйкой также называется жидкость, движущаяся в трубке тока.
Поток жидкости в соответствии со струйчатой моделью движения жидкости представляет совокупность элементарных струек.
Живым сечением потока называется поверхность, в каждой точке которой вектор скорости направлен по нормали.
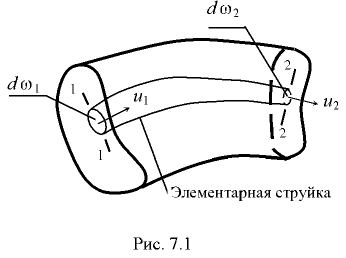
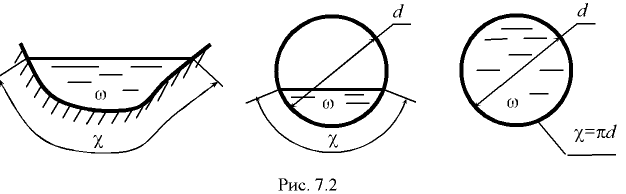
Живое сечение потока жидкости характеризуют гидравлические элементы (рис. 7.2):
площадь живого сечения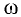 
. При решении инженерных задач потоки, как правило, бывают слабо искривленными и живое сечение в этих случаях приближенно можно принять плоским;
смоченный периметру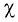 
. Это длина линии, по которой жидкость в живом сечении соприкасается с твердыми поверхностями, ограничивающими поток;
гидравлический радиус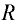 
. Это отношение площади живого сечения к смоченному периметру:
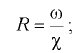
расход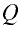 
. Это объем жидкости 
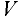, проходящий через живое сечение потока в единицу времени:
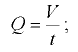
средняя по живому сечению скорость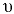 
. Это условная одинаковая во всех точках скорость, при которой расход потока будет такой же, как и при различных местных скоростях.
Расход и средняя по живому сечению скорость связаны между собой зависимостью
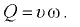
При установившемся движении форма элементарной струйки с течением времени не изменяется, отсутствует приток жидкости и ее отток через боковую поверхность трубки тока. Тогда элементарные расходы жидкости, проходящей через сечения 1-1 и 2-2 (рис. 7.1), одинаковы:
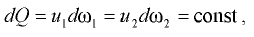
где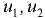 
— скорости движения частиц жидкости соответственно в сечениях 1-1 и 2-2; 
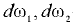— площади поперечного сечения элементарной струйки соответственно в сечениях 1-1 и 2-2.
Для установившегося движения потока жидкости (рис. 7.3), используя понятия средней скорости, имеем
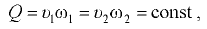
где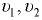 
— средние скорости течения жидкости соответственно в сечениях 1-1 и 2-2; 
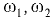— площади потока соответственно в сечениях 1-1 и 2-2.
Выражения (7.6) и (7.7) называют уравнениями постоянства расхода или уравнениями неразрывности соответственно для элементарной струйки и потока в целом.
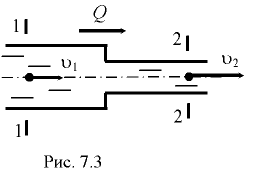
О. Рейнольдсом было установлено, что существуют два режима движения жидкости: ламинарный и турбулентный. При ламинарном режиме движения скорость частиц жидкости невелика и она движется слоями, без поперечного перемещения частиц и перемешивания жидкости. При турбулентном режиме движения частицы жидкости перемешиваются между собой и движутся беспорядочно. Потери энергии, возникающие при движении жидкости, зависят от режима движения.
Скорость потока, при которой происходит смена режимов движения жидкости, называется критической. При переходе ламинарного режима движения в турбулентный она называется верхней критической скоростью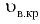 
, при переходе турбулентного режима движения в ламинарный — нижней критической скоростью 
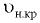. Верхняя критическая скорость больше нижней критической, колеблется в широком диапазоне и зависит от внешних условий (колебаний температуры, сотрясений трубопровода, гидравлических сопротивлений и т.д.). Нижняя критическая скорость остается практически неизменной.
Критерием для определения режима движения жидкости является безразмерное число Рейнольдса, которое для любого потока определяется через гидравлический радиус по формуле
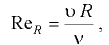
где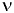 
— кинематический коэффициент вязкости жидкости; значения кинематического коэффициента вязкости некоторых смазочных масел в зависимости от температуры приведены в прил. 1.
Для напорных потоков в трубах круглого сечения число Рейнольдса выражают через внутренний диаметр трубопровода:
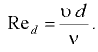
Смена режимов движения жидкости происходит при критическом значении числа Рейнольдса, которое при решении практических задач по гидравлическому радиусу принимают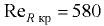 
, а по диаметру — 
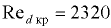. Если число Рейнольдса больше критического значения, то режим движения турбулентный, если меньше — ламинарный. Критическое значение числа Рейнольдса соответствует нижней критической скорости.
При ламинарном режиме движения напорного потока в цилиндрической трубе радиусом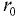 
распределение местных скоростей подчиняется параболическому закону. Максимальная скорость 
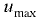имеет место на оси трубопровода. Местная скорость в слое жидкости, находящемся на расстояние 
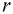от оси трубы,
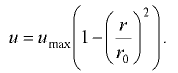
Средняя скорость
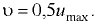
Максимальная скорость
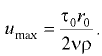
Касательные напряжения у стенки трубы
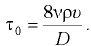
Касательные напряжения по сечению трубы распределяются по зависимости
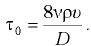
При турбулентном режиме движения напорного потока распределение осредненных скоростей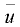 
по сечению трубы может быть приближенно принято по зависимости
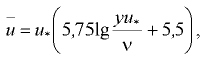
где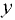 
— расстояние от стенки трубы до рассматриваемой точки (при определении значения 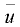у стенки трубы в формулу следует подставить достаточно малое конечное значение 
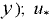— величина, имеющая размерность скорости, которая называется динамической скоростью и определяется по формуле
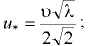
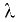— гидравлический коэффициент трения (подробнее см. разд. 9).
Зависимость между максимальной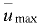 
и средней и в сечении скоростями движения имеет вид
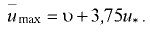
Пример задачи №7.1.
По трубе диаметром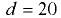 
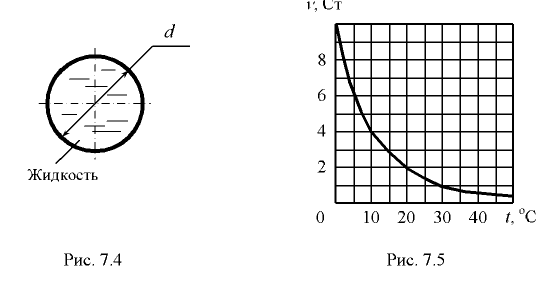
см под напором движется минеральное масло с температурой 
(рис. 7.4). Определить критическую скорость и расход, при котором происходит смена режимов движения жидкости. График зависимости кинематического коэффициента вязкости жидкости от температуры показан на рис. 7.5.
Решение:
Смена режимов произойдет при скорости, соответствующей критическому числу Рейнольдса. Для круглых напорных трубопроводов расчет выполняется по критическому числу Рейнольдса, приведенному к диаметру трубопровода,
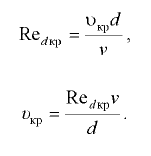
По графику (рис. 7.5) при температуре 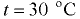находим вязкость масла 
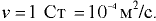Подставляя значения величин в основных единицах измерения системы СИ, получим
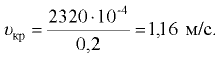
Расход определяем по формуле (7.5). Площадь живого сечения трубопровода
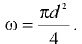
Тогда
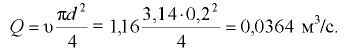
Уравнение Бернулли
Общие сведения:
При установившемся плавно изменяющемся движении реальной жидкости уравнение Бернулли для двух сечений потока 1-1 и 2-2 имеет вид
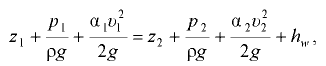
где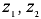 
— расстояния от плоскости сравнения до центра соответствующего сечения; 
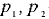— гидростатические давления соответственно в сечении 1-1 и 2-2;
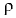— плотность жидкости; 
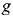— ускорение свободного падения; 
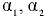— коэффициенты кинетической энергии (коэффициенты Кориолиса) соответственно в сечении 1-1 и 2-2: при ламинарном режиме движения жидкости 
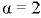. турбулентном 
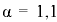, в случае, когда 
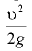мало по сравнению с потерями 
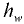или при менее точных практических расчетах, принимают 
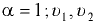— средние по живому сечению скорости соответственно в сечениях 1-1 и 2-2; 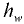— потери напора на участке между сечениями 1-1 и 2-2.
Все слагаемые уравнения Бернулли имеют линейную размерность и могут быть представлены геометрически (рис. 8.1): координата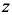 
— геометрический напор; величина 
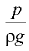пьезометрическая высота; 
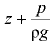— пьезометрический напор.
Линия, проходящая через свободную поверхность жидкости в пьезометрических трубках, называется пьезометрической линией. Она может понижаться или повышаться вдоль потока, возможно и горизонтальное ее положение. Линия, проходящая через свободную поверхность жидкости в скоростных трубках, называется напорной линией. Она находится выше пьезометрической на величину скоростного напора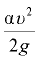 
.
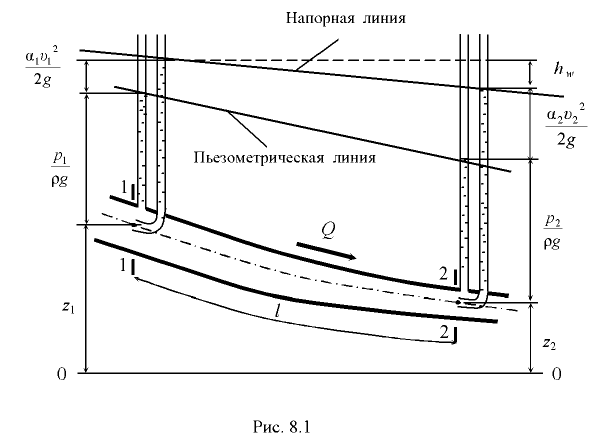
Сумма пьезометрического и скоростного напоров называется гидродинамическим напором:
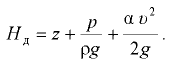
Гидродинамический напор в первом сечении больше гидродинамического напора во втором сечении на величин)’ потерь 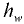. Напорная линия для потока реальной (вязкой) жидкости понижается в направлении ее движения, т.е. имеет положительный уклон.
Гидравлическим уклоном называют отношение потерь напора к длине участка, на котором ути потери происходят. Гидравлический уклон определяется но формуле
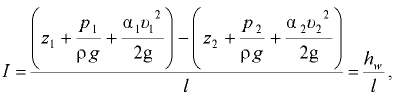
где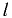 
— длина участка между сечениями 1-1 и 2-2.
Гидравлический уклон I всегда положителен, так как потери напора 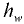>0.
Пьезометрическая линия также имеет уклон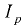 
, который называется пьезометрическим уклоном и определяется по формуле
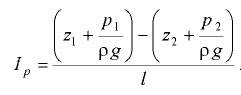
Пьезометрический уклон может быть положительным, равным нулю и отрицательным.
Пьезометрическая линия при равномерном безнапорном движении жидкости совпадает со свободной поверхностью, а напорная линия находится выше на величину скоростного напора.
С энергетической точки зрения уравнение Бернулли выражает закон сохранения энергии в потоке движущейся жидкости, а каждый член уравнения является удельной энергией, т.е. энергией, отнесенной к единице веса жидкости:
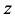— удельная потенциальная энергия положения;
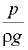— удельная потенциальная энергия давления;
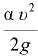— удельная кинетическая энергия.
Горизонтальную плоскость сравнения при составлении уравнения Бернулли целесообразно проводить через ось потока, свободную поверхность жидкости в нижнем резервуаре или ниже всего потока жидкости. Расчетные поперечные сечения выбираются и нумеруются по течению жидкости. При их выборе следует стремиться к тому, чтобы в уравнение Бернулли входили неизвестные величины и как можно больше известных. В большинстве случаев при расчете движения жидкости с разными скоростями в живых сечениях потока наряду с уравнением Бернулли используется и уравнение неразрывности (7.7).
Пример задачи №8.1.
По горизонтальному трубопроводу переменного сечения движется жидкость (рис. 8.2), плотность которой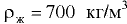 
. Диаметр в сечении 1-1 трубопровода 
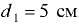, а в сечении 2-2 
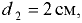разность уровней в дифференциальном манометре, заполненном глицерином плотностью 
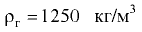, составляет 
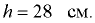. Определить скорость движения жидкости в сечении 2-2 трубопровода. Потери напора не учитывать.
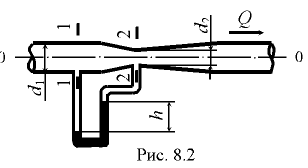
Решение:
Составим уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0. За плоскость сравнения целесообразно выбрать горизонтальную плоскость, совпадающую с осью трубопровода, а сечения назначить в широкой и узкой частях трубопровода в местах присоединения дифференциального манометра. Тогда
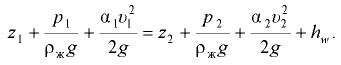
По условию задачи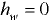 
, для горизонтального трубопровода 
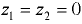. С достаточной степенью точности можно принять 
.
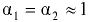Разность давлений в сечениях с учетом разных жидкостей и их плотности в дифференциальном манометре
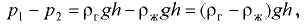
где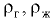 
— плотность соответственно глицерина и жидкости в дифференциальном манометре.
Из уравнения неразрывности потока
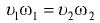
выразим
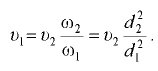
Тогда уравнение Бернулли принимает вид
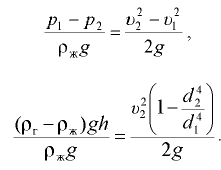
Отсюда
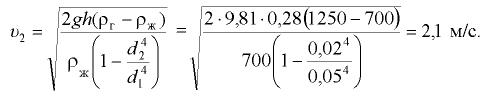
Гидравлические сопротивления
Общие сведения:
При движении реальной жидкости необходимо учитывать потери энергии на преодоление сопротивления движению жидкости. Различают два вида основных сопротивлений:
- сопротивления, проявляющиеся по длине потока, обусловленные силами трения частиц жидкости друг о друга и о стенки, ограничивающие поток. Им соответствуют потери напора на трение по длине потока
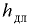; - сопротивления, обусловленные препятствиями на отдельных ограниченных участках потока, где наблюдается изменение направления или величины скорости (расширение или сужение потока, поворот потока, наличие задвижек, кранов, вентилей и т.д.). Им соответствуют потери напора на преодоление местных сопротивлений
.
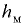Общие потери напора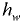 
складываются из суммы потерь напора на трение по длине и суммы местных потерь напора на рассматриваемом участке пути потока:
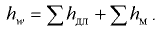
Потери напора на трение по длине в круглой трубе в общем случае определяются по формуле Дарси:
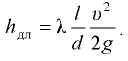
Коэффициент гидравлического трения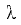 
определяется в зависимости от режима движения жидкости и зоны (области) гидравлических сопротивлений, в которой работает трубопровод.
Для ламинарного режима
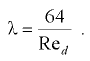
При турбулентном режиме различают три зоны (области) гидравлических сопротивлений.
При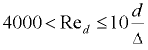 
(зона гидравлически гладких труб, 
— абсолютная шероховатость стенок трубопровода)
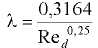
формула Блазиуса.
При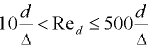 
(переходная зона от гидравлически гладких труб к гидравлически шероховатым)
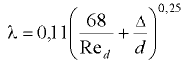
формула Альтшуля.
При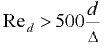 
(зона гидравлически шероховатых труб, или квадратичная зона сопротивлении
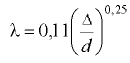
формула Шифринсона.
Существуют также и другие зависимости [7-9]. Для расчета сопротивлений при движении нефти по трубам используются зависимости, приведенные в [10]. Коэффициент гидравлического трения 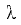можно определить по графику при л. 6.
Потери напора для квадратичной зоны сопротивлений можно определить через удельное сопротивление трубопровода или расходную характеристику по формуле
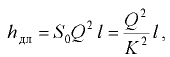
где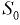 
— удельное сопротивление трубопровода.
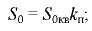
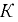— расходная характеристика,
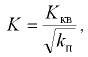
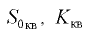— удельное сопротивление и расходная характеристика для квадратичной зоны сопротивления; 
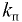— поправочный коэффициент, определяемый в зависимости от скорости
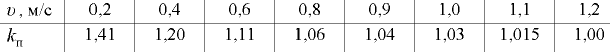
В квадратичной области сопротивления (при скоростях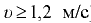 
) значения 
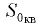для бывших в эксплуатации стальных груб приведены в прил. 7 [11,12).
Значения абсолютной шероховатости трубопроводов приведены в табл. 9.1.
Потери напора в местных сопротивлениях определяются по формуле Вейебаха
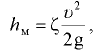
где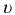 
— средняя по живому сечению скорость (обычно в сечении трубопровода за местным сопротивлением).
Значения коэффициентов местных сопротивлений зависят от вида местного сопротивления и в некоторых случаях от числа Рейнольдса. В большинстве случаев определяются экспериментально и лишь для некоторых видов сопротивлений их можно определить теоретически. Значения коэффициентов местных сопротивлений в квадратичной зоне гидравлических сопротивлений приведены в [7] и другой справочной и учебной литературе.
Внезапное расширение трубопровода. Коэффициент местного сопротивления при внезапном расширении трубопровода (рис. 9.1), отнесенный к скорости за сопротивлением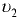 
, определяется но формуле
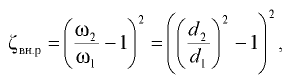
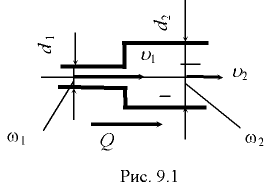
отнесенный к скорости до сопротивления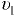 
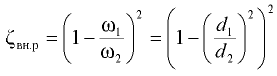
где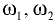 
— площади живого сечения трубопровода соответственно перед и за сопротивлением.
Значения коэффициента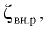 
, рассчитанные по формуле (9.10), приведены в табл. 9.2.
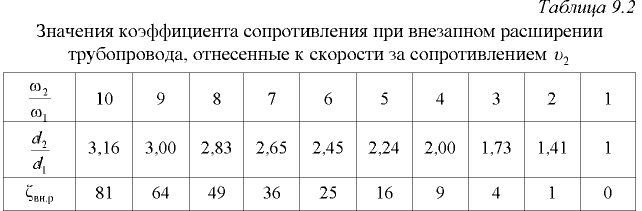
Внезапное сужение трубопровода. Коэффициент местного сопротивления при внезапном сужении трубопровода, отнесенный к скорости 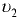(рис. 9.2), определяется по формуле
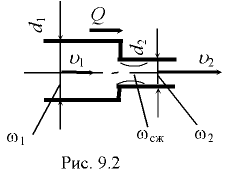
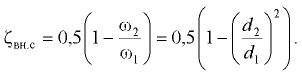
Коэффициент сжатия можно определить по формуле, приведенной в [7]. Значения коэффициента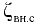 
, рассчитанные по формуле (9.12), приведены в табл. 9.3.
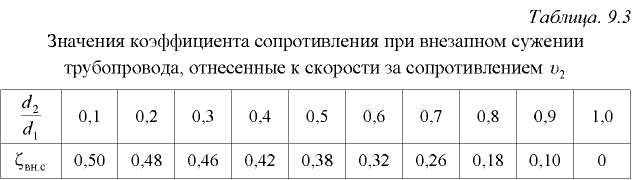
Диафрагма на цилиндрическом трубопроводе. Для уменьшения расхода жидкости на участке трубопровода служит диафрагма (рис. 9.3). Диафрагма представляет собой пластинку с отверстием в центре, диаметр которого меньше диаметра трубопровода. Коэффициент сопротивления диафрагмы
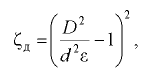
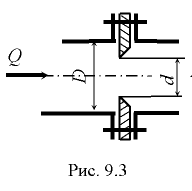
где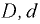 
— диаметры соответственно трубопровода и отверстия в диафрагме; 
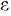— коэффициент сжатия струи, определяется по формуле А.Д. Альтшуля [7]
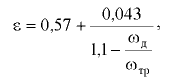
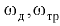— площади живого сечения соответственно диафрагмы и трубопровода.
Значения коэффициента сопротивления диафрагмы, рассчитанные по формуле (9.13), приведены в табл. 9.4.
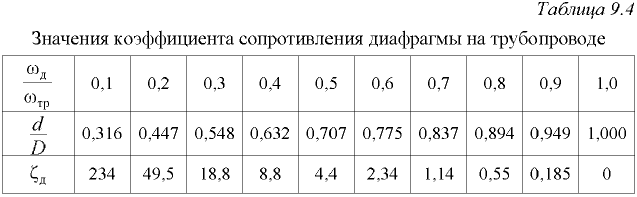
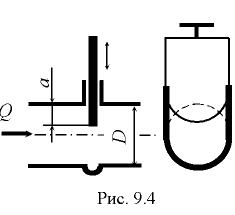
Задвижка и а трубопроводе. Для регулирования расхода на трубопроводах устанавливают задвижки (рис. 9.4). Коэффициент сопротивления задвижки зависит от степени ее закрытия 
. Значения коэффициента (но экспериментальным данным) приведены в табл. 9.5.
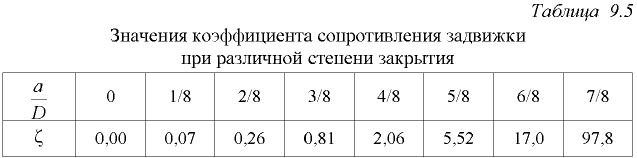
Экспериментальные значения коэффициентов местных сопротивлений наиболее часто встречающихся сопротивлений приведены в табл. 9.6.
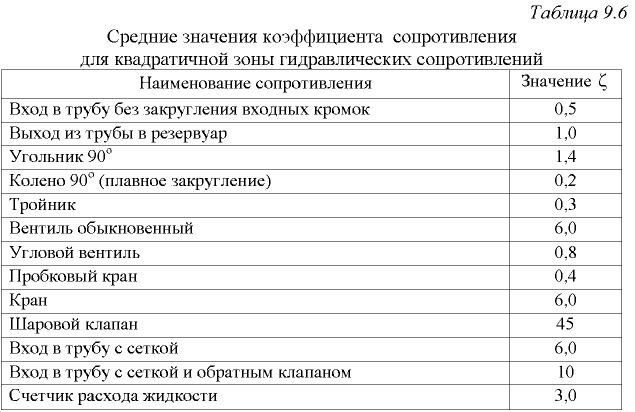
Примечание. Значения коэффициента сопротивления для вентилей и кранов приведены для положения «открыто».
Пример задачи №9.1.
Из напорного бака, в котором поддерживается постоянный уровень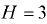 
м, по наклонному трубопроводу переменного сечения (рис. 9.5) движется вода. Диаметры участков трубопровода 
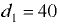мм,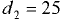 
мм, длины соответственно 
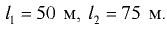. Начало трубопровода расположено выше его конца на величину 
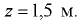Определить расход воды в трубопроводе, если коэффициент гидравлического трения 
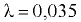для обоих участков трубопровода. Местными потерями напора пренебречь.
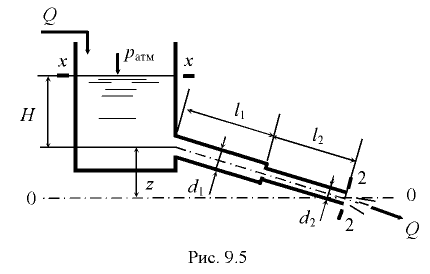
Решение:
Составим уравнение Бернулли для сечений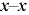 
и 2-2 относительно горизонтальной плоскости сравнения 0-0. Плоскость сравнения целесообразно провести через конец трубопровода. Сечение 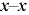назначаем по уровню в напорном баке, а сечение 2-2 на выходе из трубопровода. Тогда
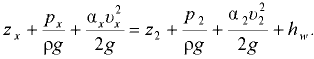
Здесь
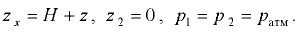
С достаточной степенью точности можно принять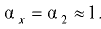 
Скорость 
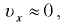так как площадь в сечении 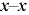существенно больше площадей живого сечения в трубопроводе. Потери напора по длине равняются сумме потерь на первом и втором участках трубопровода и определяются но формуле
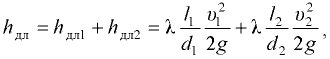
где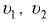 
— средние по живому сечению скорости соответственно на участках трубопровода длиной 
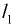и 
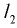, диаметром 
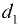и 
.
И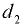з уравнения неразрывности потока
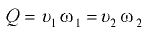
выразим скорости
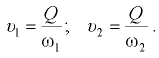
Произведя подстановку в исходное уравнение Бернулли, получаем
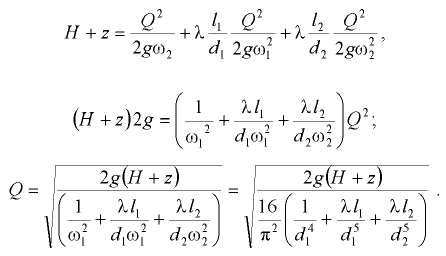
После подстановки численных значений получаем
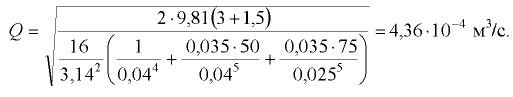
Теория из учебников и готовые задачи на продажу тут.
Истечение жидкости через отверстия и насадки
Общие сведения:
Законы истечения жидкости через отверстия применяются при решении многих технических задач: измерении расхода жидкости, создании мощной дальнобойной струи для размьюа грунта, расчете распространения струи в массе жидкости, обеспечении заданного времени опорожнения резервуаров, конструировании сопел, форсунок и в других случаях.
Различают отверстия малые и большие. Если напор превышает 10 наибольших вертикальных размеров отверстия, то отверстие — малое, в противном случае — большое. Отверстие считается в тонкой стенке в случае, если толщина стенки не влияет на условия истечения, т. е. вытекающая жидкость касается только кромки отверстия. Это обеспечивается либо срезом кромок под острым углом, либо при толщине стенки меньше 0,2 диаметра отверстия. Рассмотрим истечение жидкости через малое отверстие в тонкой стенке (рис. 10.1).
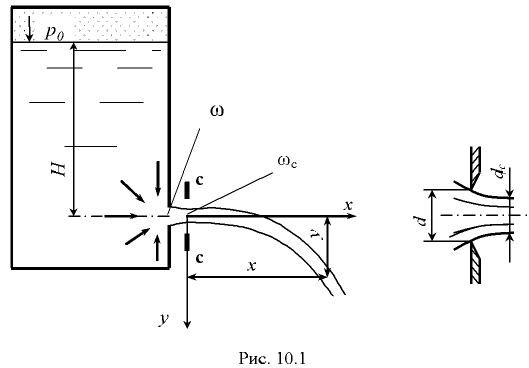
При истечении жидкости из отверстия струя сжимается до сечения 
. Сжатие струи обусловлено инерцией частиц жидкости, движущихся по криволинейным траекториям, и характеризуется коэффициентом сжатия
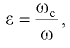
где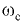 
— площадь струи в сжатом сечении; 
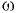— площадь отверстия.
Если отверстие круглое, то расстояние от внутренней поверхности стенки до сжатого сечения приблизительно равно (0,5… 1 Д)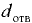
.
Сжатие струи может быгъ полным и неполным. Полное сжатие происходит со всех сторон, когда отверстие удалено от боковых стенок или дна резервуара (рис. 10.2, а). Неполное сжатие наблюдается, когда отверстие примыкает к боковой стенке или дну резервуара, т.е. сжатие струи с одной стороны (рис. 10.2, б, в) или нескольких сторон (рис. 10.2, г) отсутствует.
При истечении жидкости через отверстие, примыкающее к вертикальной стенке, частицы жидкости, двигаясь вдоль стенки по инерции стремятся двигаться по вертикали. В результате наблюдается сжатие струи сверху и сбоку.
При истечении жидкости через отверстие, примыкающее к дну сосуда, частицы жидкости, двигаясь вдоль донной стенки, продолжают двигаться в том же направлении, не вызывая сжатия струи с нижней части.
Если отверстие примыкает к боковой стенке и дну сосуда одновременно, то сжатие струи будет отсутствовать с двух сторон.
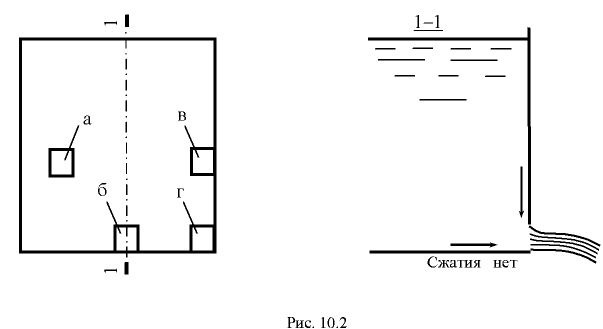
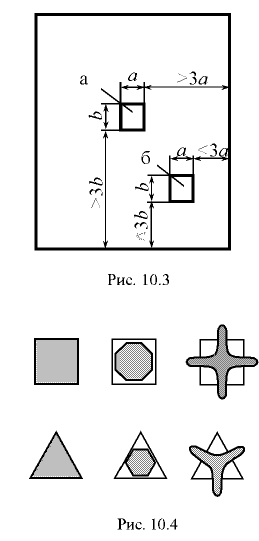
Полное сжатие может быть совершенным и несовершенным. При совершенном сжатии стенки и дно резервуара не оказывают влияния на степень сжатия струи. Такое сжатие получается, когда отверстие удалено от боковой стенки и дна резервуара более чем на три поперечных размера отверстия (рис. 10.3, а). При несовершенном сжатии стенки и дно резервуара влияют на степень сжатия струи. В этом случае отверстие удалено от боковой стенки или дна резервуара менее чем на три попереч-ных размера (рис. 10.3, б).
При истечении форма поперечного сечения струи изменяется. Изменение формы поперечного сечения струи вдоль течения называется инверсией струи. Примеры изменения формы поперечного сечения струи для квадратного и треугольного отверстий показаны на рис. 10.4. Тонкими линиями показаны контуры отверстий, штриховкой — поперечное сечение струи в различных сечениях вдоль течения, при постоянном напоре. Истечение жидкости при постоянном напоре. Скорость струи в сжатом сечении при истечении через отверстие в общем случае определяется по формуле
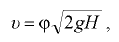
где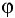 
— коэффициент скорости; 
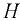— напор истечения.
В случае истечения из закрытого резервуара в газообразную среду (см. рис. 10.1) напор истечения равен разности пьезометрических напоров со стороны истекаемой жидкости и среды, в которую происходит истечение,
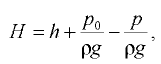
где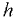 
— глубина погружения центра тяжести выходного отверстия от свободной поверхности истекаемой жидкости: 
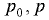— давление соответственно на поверхности жидкости и в среде, в которую происходит истечение.
При истечении в атмосферу из открытого резервуара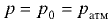 
и 
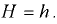
Коэффициент скорости
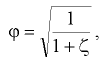
где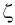 
— коэффициент сопротивления.
Расход жидкости при истечении через отверстия
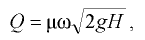
где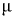 
— коэффициент расхода,
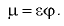
Траекторией струи называют ось струи жидкости, свободно падающей после истечения через отверстие. Координаты оси струи 
и 
связаны между собой соотношениями
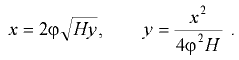
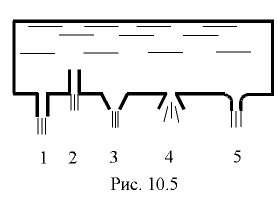
Если к отверстию присоединить (насадить) короткую трубу того же диаметра, что и отверстие, то характер истечения существенным образом изменится. Такие трубы называют насадками, они имеют длину, равную (3,,.6)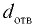
. На рис. 10.5 показаны основные типы насадков: 1 — цилиндрический внешний; 2 — цилиндрический внутренний; 3 — конический сходящийся; 4 — конический расходящийся; 5 — коноидальный. Присоединение насадка к отверстию изменяет расход жидкости, следовательно, изменяет время опорожнения резервуара, дальность полета струи и другие параметры.
Для расчета параметров истечения жидкости через насадки используются приведенные выше зависимости, при определении расхода принимается площадь на выходе насадка. Коэффициенты сжатия, скорости, расхода и сопротивления для отверстий и насадков (квадратичная зона истечения) приведены в прил. 8.
Значения коэффициентов истечения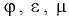 
круглого малого отверстия зависят от формы его кромок, условий подтока жидкости к отверстию и числа Рейнольдса, определяемого как
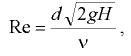
где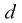 
— диаметр отверстия.
При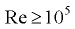 
число Рейнольдса практически не влияет на коэффициенты истечения (квадратичная зона истечения).
Более подробно вопросы истечения жидкости через отверстия и насадки рассмотрены в работах [14, 15].
Коэффициенты истечения 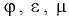для цилиндрических насадков в прил. 8 приведены при безотрывном режиме истечения. В этом случае диаметр струи на выходе из насадка равен диаметру отверстия. При критическом напоре истечения для внешнего цилиндрического насадка струя после сжатия уже не расширяется, а сохраняет цилиндрическую форму и перемещается внутри насадка, не соприкасаясь с его стенками. Истечение становится точно таким же, как и из отверстия в тонкой стенке, с теми же значениями коэффициентов.
При безотрывном истечении жидкости через цилиндрический насадок внутри насадка образуется сжатое сечение и вакуум. При этом напор истечения
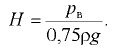
Из формулы (10.9) следует, что с увеличением напора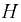 
возрастает и величина вакуума, которая связана с давлением в сжатом сечении 
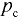, т.е. 
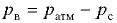. Критический напор истечения при понижении давления в сжатом сечении до давления насыщенных паров жидкости
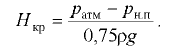
Для холодной воды давление насыщенных паров близко к нулю и критический напор
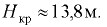
При истечении под уровень [11]
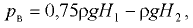
где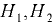 
— гидростатический напор соответственно со стороны истечения и со стороны подтопления.
Истечение жидкости при переменном напоре. При истечении жидкости при переменном напоре (рис. 10.6) часто требуется определить время наполнения или опорожнения резервуара.
В общем случае, когда резервуар имеет произвольные очертания, время опорожнения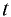 
части резервуара через отверстие может быть определено методами численного интегрирования выражения
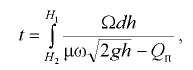
где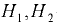 
— уровни жидкости в резервуаре соответственно в начальный и конечный моменты времени; 
— площадь горизонтального сечения резервуара (площадь поверхности жидкости в резервуаре);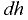 
— изменение уровня жидкости в резервуаре за время 
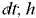— текущее значение уровня жидкости в резервуаре; 
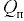— расход жидкости, поступающей в резервуар.
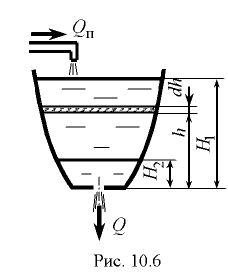
В том случае, когда сосуд имеет правильную геометрическую форму (параллелепипед, цилиндр, шар), при известной величине притока жидкости интеграл (10.12) имеет решения.
В случае отсутствия притока (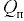 = 0) для резервуаров с постоянной площадью зеркала жидкости (призматические и вертикальные цилиндрические) время частичного опорожнения через отверстие
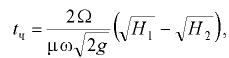
а время полного опорожнения
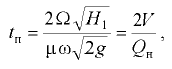
где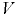 
— объем жидкости в резервуаре в начальный момент времени; 
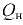— расход жидкости в начальный момент времени.
Для горизонтального цилиндрического резервуара
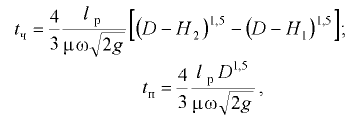
где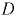 
— диаметр резервуара; 
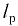— длина образующей цилиндрического резервуара.
Для сферического резервуара
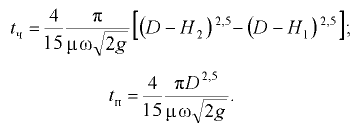
В работах [16-19] приведены задачи по истечению жидкости при несовершенном, неполном, сжатии, а также через большие отверстия. Рассмотрен ряд примеров решения.
Пример задачи №10.1.
Вода вытекает из закрытого резервуара в атмосферу через отверстие диаметром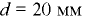 
(рис. 10.7). Глубина погружения центра отверстия 
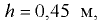избыточное давление на поверхности жидкости 
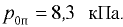. Определить расход жидкости, а также необходимое избыточное давление для пропуска того же расхода, если к отверстию присоединить цилиндрический внешний насадок длиной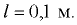 
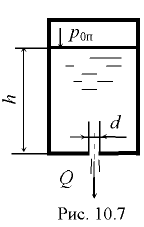
Решение:
Расход при истечении жидкости через отверстие определяется по формуле (10.5). В случае истечения жидкости из закрытого резервуара в атмосферу формула принимает вид
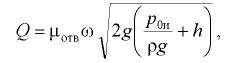
где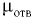 
— коэффициент расхода, для круглого отверстия 
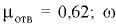— площадь отверстия,
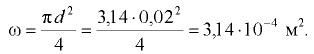
После подстановки численных значений получаем
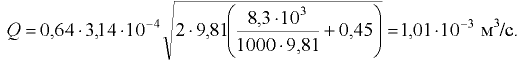
Если к отверстию в дне резервуара присоединить цилиндрический внешний насадок того же диаметра, то формула (10.5) принимает вид
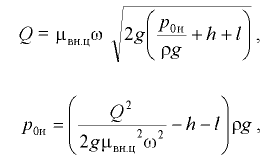
где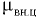 
— коэффициент расхода, для внешнего цилиндрического насадка, 
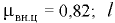— длина насадка.
После подстановки численных значений имеем
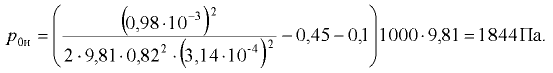
Эти страницы вам могут помочь:
