Оглавление:
Правило Лопиталя
Теорема 8.1. Пусть
1) функции 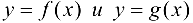 определены и непрерывны в проколотой окрестности
определены и непрерывны в проколотой окрестности 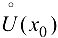 ;
;
2) существуют конечные производные 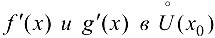 ;
;
3) 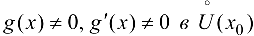 ;
;
4) 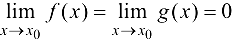 .
.
Тогда если существует 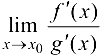 . то существует
. то существует 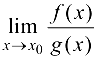 и имеет место равенство
и имеет место равенство
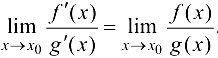
Доказательство.
Доопределим функции 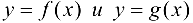 в точке
в точке 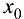 , полагая
, полагая 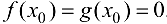 .
.
Тогда функции 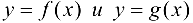 непрерывны в точке
непрерывны в точке 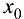 . Используя теорему Коши (теорема 7.3), получим
. Используя теорему Коши (теорема 7.3), получим
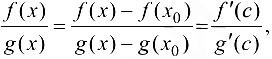
где точка с будет удовлетворять условиям 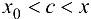 или
или 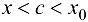 .
.
Если 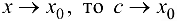 , поэтому, согласно условию теоремы,
, поэтому, согласно условию теоремы,
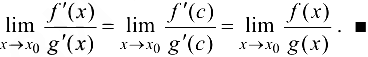
Теорема 8.1 формулирует правило раскрытия неопределенности типа 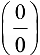 .
.
Замечание 8.1. Если производные 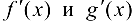 удовлетворяют тем же требованиям, что и сами функции
удовлетворяют тем же требованиям, что и сами функции 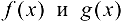 , то правило Лопиталя можно применять повторно. При этом получаем
, то правило Лопиталя можно применять повторно. При этом получаем
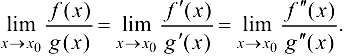
Пример 8.1.
Найти предел 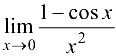 .
.
Решение:
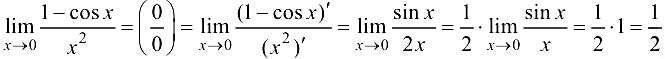
Ответ: 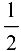 .
.
Пример 8.2.
Найти предел 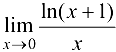 .
.
Решение:
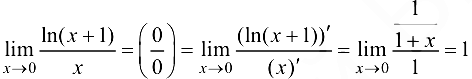
Ответ: 1.
Пример 8.3.
Найти предел 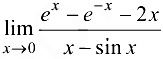 ;
;
Решение:
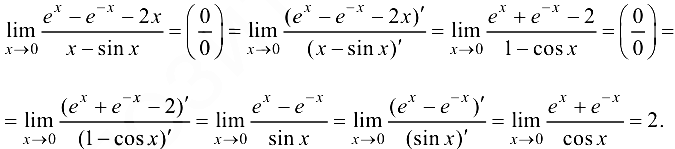
Ответ: 2.
Теорема 8.2*. Пусть
1) функции 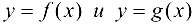 определены и непрерывны в проколотой окрестности
определены и непрерывны в проколотой окрестности 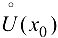 ;
;
2) существуют конечные производные 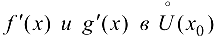 ;
;
3) 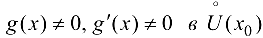 ;
;
4) 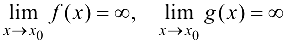
Тогда, если существует 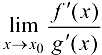 , то существует
, то существует 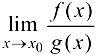 и имеет место равенство
и имеет место равенство
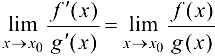
Теорема 8.2 формулирует правило раскрытия неопределенности типа 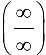
Замечание 8.2. Правило Лопиталя справедливо и в случаях 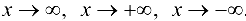 .
.
Пример 8.4.
Найти предел 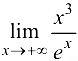 .
.
Решение:
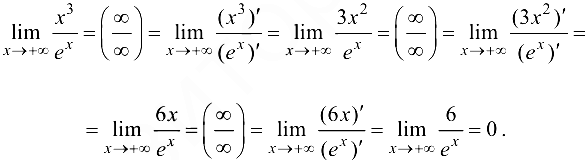
Ответ: 0.
Пример 8.5.
Найти предел 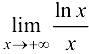 .
.
Решение:
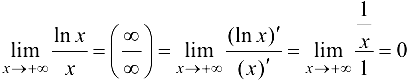
Ответ: 0.
Пример 8.6.
Найти предел 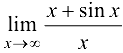 .
.
Решение:
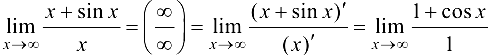
Полученный предел не существует, так как при 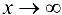 функция
функция 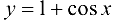 не стремится ни к какому предельному значению, а колеблется между 0 и 2. Правило Лопиталя не дает результатов.
не стремится ни к какому предельному значению, а колеблется между 0 и 2. Правило Лопиталя не дает результатов.
Рассмотрим другой подход к вычислению предела.
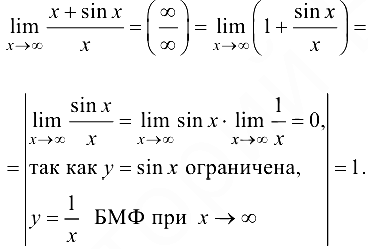
Ответ: 1.
Заметим, что правило Лопиталя дает также возможность раскрыть неопределенности типа 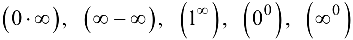 предварительно приведя их к виду
предварительно приведя их к виду 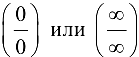 .
.
Пример 8.7.
Найти предел 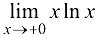 .
.
Решение:
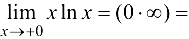
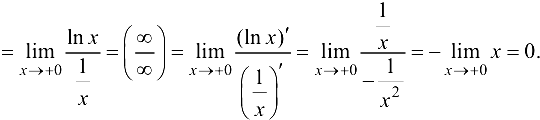
Ответ: 0.
Пример 8.8.
Найти предел 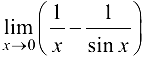
Решение:
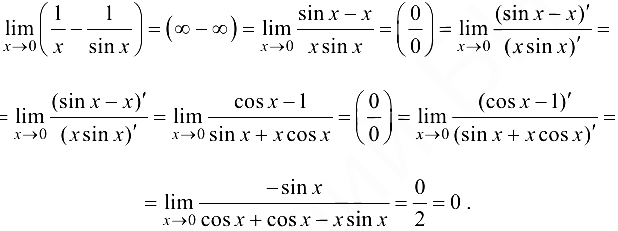
Ответ: 0.
Пример 8.9.
Найти предел 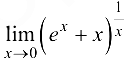 .
.
Решение:
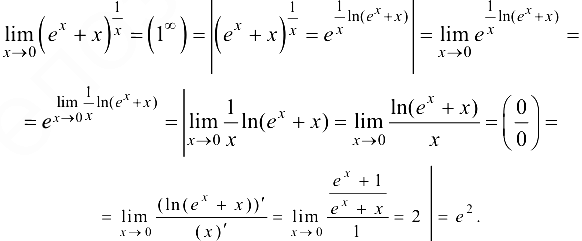
Ответ: 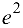 .
.
Пример 8.10.
Найти предел 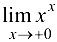 .
.
Решение:
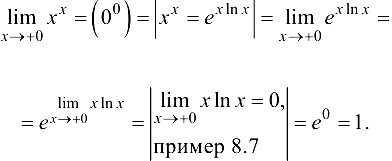
Ответ: 1.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:

