Соответствие 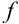 , которое каждой паре значений переменных
, которое каждой паре значений переменных  и
и  , принадлежащей некоторому множеству пар
, принадлежащей некоторому множеству пар  , сопоставляет единственное число
, сопоставляет единственное число 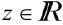 , называется функцией двух переменных, определенной на множестве
, называется функцией двух переменных, определенной на множестве  со значениями в
со значениями в 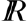 .
.
Символически функция двух переменных обозначается следующим образом:  . При этом хну называются независимыми переменными (аргументами), a
. При этом хну называются независимыми переменными (аргументами), a 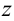 — зависимой переменной (функцией).
— зависимой переменной (функцией).
Множество  пар значений, которые могут принимать независимые переменные
пар значений, которые могут принимать независимые переменные  и
и  (значение функции при этом является числом), называется областью определения функции двух переменных.
(значение функции при этом является числом), называется областью определения функции двух переменных.
Для различных функций двух переменных область определения имеет разный вид. Она может представлять собой конечную или бесконечную часть плоскости, ограниченную одной или несколькими непрерывными линиями — границами области. Возможен случай, когда какая — то из границ превращается в одну точку. Так, областью определения функции 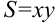 из задачи 1 с учетом ее геометрического смысла является множество точек плоскости первой координатой четверти за исключением точек осей координат:
из задачи 1 с учетом ее геометрического смысла является множество точек плоскости первой координатой четверти за исключением точек осей координат:
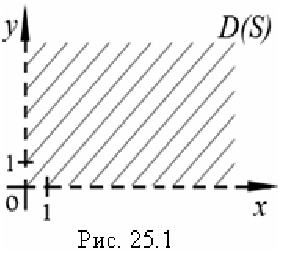
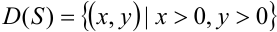 (рис. 25.1).
(рис. 25.1).
Множество всех значений, принимаемых  в области ее определения, называется областью значений функции
в области ее определения, называется областью значений функции  и обозначается
и обозначается 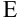 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Несобственные интегралы II рода. |
| Задачи, приводящие к понятию функции нескольких переменных. |
| Способы задания функции двух действительных переменных. |
| Предел функции двух действительных переменных. |
