Положение плоскости относительно плоскостей проекций.
Плоскости общего положения и плоскости частного положения
Относительно плоскостей проекций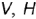 
и 
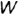плоскости в пространстве могут занимать семь различных положений — общее и шесть частных — и имеют соответствующие названия и характерные признаки проекций на чертежах. Следовательно, по заданным проекциям плоскости можно представить ее положение в пространстве, т.е. «прочитать» чертеж плоскости.
Плоскость, не перпендикулярная ни одной из плоскостей проекций (см. рис. 4.21-4.24), называется ПЛОСКОСТЬЮ ОБЩЕГО ПОЛОЖЕНИЯ.
!!.’Запомните характерные признаки плоскости общего положения на чертеже — ни одна ее проекция не вырождается в линию и каждая проекция искажает величину той формы, плоскость которой задана на чертеже.
Плоскости частного положения, перпендикулярные одной плоскости проекций, называются ПРОЕЦИРУЮЩИМИ ПЛОСКОСТЯМИ
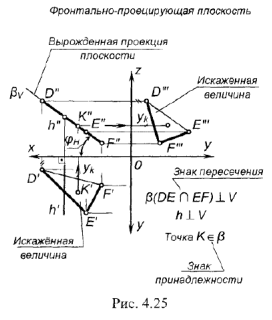
ФРОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬ перпендикулярна фронтальной плоскости проекций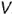 
. На рис. 4.25 плоскость задана двумя пересекающимися прямыми 
и 
; горизонталь плоскости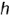 
преобразуется здесь во фронтально-проецирующую прямую 
.
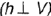!!Запомните характерные признаки фронтально-проецирующей плоскости на чертеже — ее фронтальная проекция представляет собой прямую (вырожденная проекция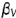 
) наклоненную к оси проекций 
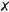, и определяет угол наклона плоскости к плоскости проекций 
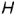. Горизонтальная и профильная проекции плоскости представляют собой искаженную по величине форму, которой эта плоскость задана на чертеже.
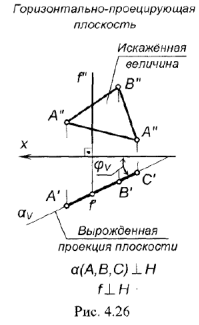
ГОРИЗОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬ перпендикулярна горизонтальной плоскости проекций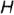 
. На рис. 4.26 плоскость задана треугольником 
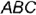; фронталь плоскости 
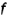преобразуется в горизонтально-проецирующую прямую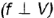 
!!! Запомните характерные признаки горизонтально-проецирующей плоскости на чертеже — ее горизонтальная проекция представляет собой прямую (вырожденная проекция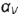 
), наклоненную к оси проекций 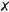, и определяет угол наклона плоскости к плоскости проекций 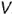. Фронтальная и профильная (не показана) проекции плоскости представляют собой искаженную по величине форму, которой эта плоскость задана па чертеже.
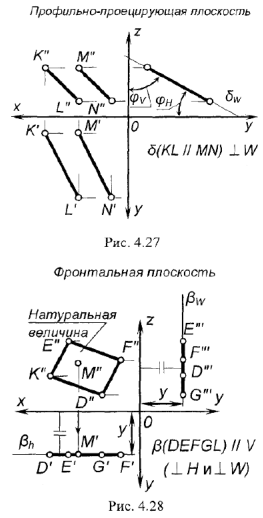
ПРОФИЛЬНО-ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬ перпендикулярна профильной плоскости проекций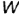 
. На рис. 4.27 плоскость задана двумя параллельными прямыми 
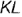и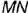 
; фронталь и горизонталь плоскости преобразуются в профильно-проецирующие прямые.
!!! Запомните характерные признаки профильно-проецирующей плоскости на чертеже — ее профильная проекция представляет собой прямую (вырожденная проекция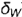 
), наклоненную к осям проекци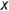й 
и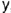 
, и определяет углы па-клона плоскости к плоскостям проекци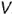й и 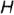. Фронтальная и горизонтальная проекции этой плоскости представляют собой искаженную по величине форму, которой эта плоскость задана на чертеже.
I Плоскости частного положения, перпендикулярные двум плоскостям проекций и параллельные третьей плоскости проекций, называются ПЛОСКОСТЯМИ УРОВНЯ.
ФРОНТАЛЬНАЯ ПЛОСКОСТЬ УРОВНЯ параллельна фронтальной плоскости проекций 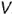и перпендикулярна плоскостям проекци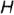й и 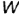. На рис. 4.28 фронтальная плоскость уровня задана параллелограммом 
; фронтальная проекция этой плоскости является ее натуральной величиной.
!!! Запомните характерные признаки фронтальной плоскости на чертеже -ее горизонтальная и профильная проекции проецируются в прямые (вырожденные проекци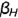и 
и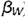 
), параллельные соответственно осям проекци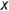й и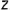 
.
ГОРИЗОНТАЛЬНАЯ ПЛОСКОСТЬ УРОВНЯ параллельна горизонтальной плоскости проекций 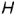и перпендикулярна плоскостям проекци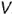й и .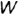
На рис. 4.29 горизонтальная плоскость уровня задана треугольником : горизонтальная проекция этой плоскости является ее натуральной величиной.
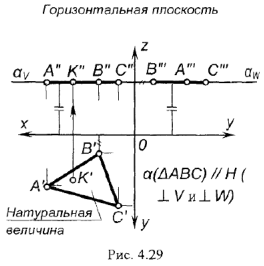
!!! Запомните характерные признаки горизонтальной плоскости на чертеже — ее фронтальная и профильная проекции проецируются в прямые (вырожденные проекци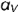и 
и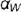 
), параллельные соответственно осям проекци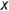й и .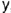
ПРОФИЛЬНАЯ ПЛОСКОСТЬ УРОВНЯ параллельна плоскости проекций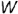 
и перпендикулярна плоскостям проекци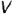й 
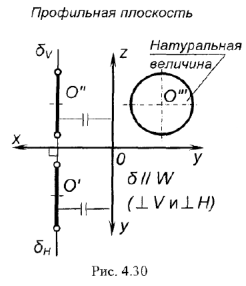
и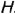 
. На рис. 4.30 плоскость задана кругом с центром в точке 
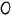и ее профильная проекция имеет натуральную величину этого круга.
!!! Запомните характерные признаки профильной плоскости на чертеже — ее фронтальная и горизонтальная проекции представляют собой прямые (вырожденные проекци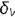и 
и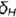 
), перпендикулярные оси проекций 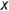и параллельные осям 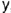и .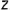
Эта теория взята со страницы задач по начертательной геометрии:
Возможно эти страницы вам будут полезны:
