Полином Тейлора. Формулы Тейлора и Маклорена
Пусть функция 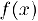 определена и n + 1 раз дифференцируема в некотором интервале, содержащем точку ®q. Найдем полином степени n, который вместе со своими производными до n-ой включительно, совпадает с соответствующими значениями функции и се производных в точке
определена и n + 1 раз дифференцируема в некотором интервале, содержащем точку ®q. Найдем полином степени n, который вместе со своими производными до n-ой включительно, совпадает с соответствующими значениями функции и се производных в точке 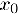 (полином Тейлора в точке
(полином Тейлора в точке 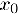 ). Этот полином нам удобно искать в виде:
). Этот полином нам удобно искать в виде:
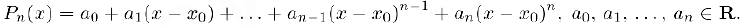
Вычислим коэффициенты полинома Тейлора. С одной стороны, 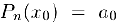 . с другой
. с другой 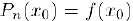 , поэтому
, поэтому 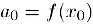 . Далее будем последовательно дифференцировать полином
. Далее будем последовательно дифференцировать полином 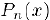 и приравнивать его производные в точке
и приравнивать его производные в точке 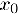 соответствующим производным функции
соответствующим производным функции 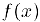
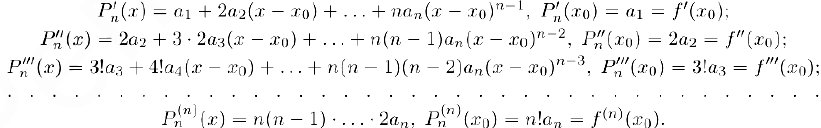
Таким образом,
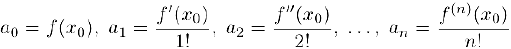
и, следовательно,
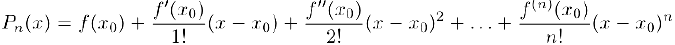
— полипам Тейлора а точке 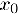 .
.
Найдем разность 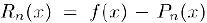 , т. е. величину ошибки, которую мы совершаем, заменив функцию ее полиномом Тейлора. Рассмотрим функции
, т. е. величину ошибки, которую мы совершаем, заменив функцию ее полиномом Тейлора. Рассмотрим функции
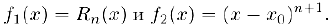
Заметим, прежде всего, что дня них
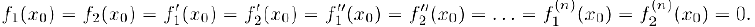
Применим последовательно теорему Коши (§3) к функциям 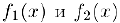 и их производным до т—ой включительно на соответствующих отрезках:
и их производным до т—ой включительно на соответствующих отрезках:
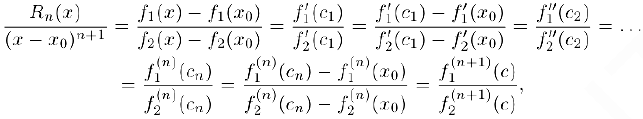
где 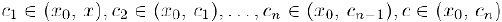 Отсюда, учитывая, что
Отсюда, учитывая, что
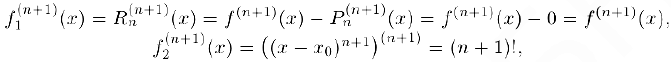
получим:
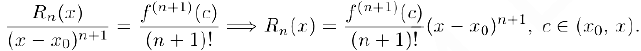
Таким образом.
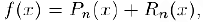
т. e. данная n + 1 раз дифференцируемая в интервале, содержащем точку 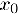 , функция
, функция 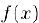 представляется в этом интервале в виде суммы своего полинома Тейлора
представляется в этом интервале в виде суммы своего полинома Тейлора 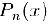 и погрешности
и погрешности 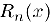 :
:
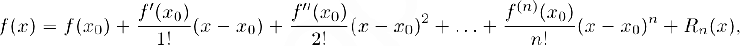
где
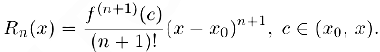
Найденное представление называется формулой Тейлора. порядка n для функции 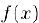 в точке
в точке 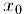 с остатком
с остатком 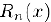 в форме Лагранжа. В частном случае при
в форме Лагранжа. В частном случае при 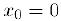 из (1) следует формула Маклорена:
из (1) следует формула Маклорена:
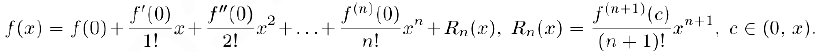
Если потребовать, чтобы функция 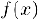 была
была  раз дифференцируема в некотором интервале, содержащем точку
раз дифференцируема в некотором интервале, содержащем точку 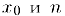 раз дифференцируема в точке
раз дифференцируема в точке 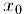 , то для этой функции имеет место формула Тейлора с остатком в форме Пеано:
, то для этой функции имеет место формула Тейлора с остатком в форме Пеано:
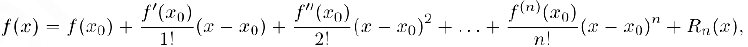
в которой
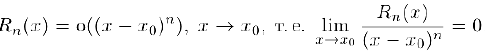
Замечание 1. Из определения полинома Тейлора следует, что он для функции находится однозначно и полином Тейлора для суммы (разности) функций равен сумме (разности) их полиномов Тейлора.
Замечание 2. Подстановка 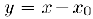 сводит задачу разложения функции
сводит задачу разложения функции 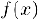 по формуле Тейлора к задаче представления функции
по формуле Тейлора к задаче представления функции 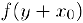 с помощью формулы Маклорена.
с помощью формулы Маклорена.
Так как величина 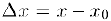 представляет собой приращение аргумента в точке
представляет собой приращение аргумента в точке 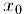 , то мы можем переписать формулу Тейлора (3) в дифференциалах (§2, пункт 3):
, то мы можем переписать формулу Тейлора (3) в дифференциалах (§2, пункт 3):
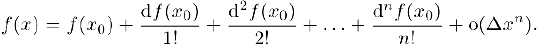
Из многочисленных приложений формулы Тейлора отметим здесь возможность приближенного вычисления значений функции с любой точностью. Действительно, если задана точность вычисления 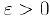 . то в качестве приближенного значения функции мы можем взять значение ее полинома Тейлора, подобрав n таким, чтобы остаток формулы Тейлора был меньше по абсолютной величине, чем точность
. то в качестве приближенного значения функции мы можем взять значение ее полинома Тейлора, подобрав n таким, чтобы остаток формулы Тейлора был меньше по абсолютной величине, чем точность 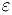 . Более удобной в этом отношении является формула (1), так как мы можем оценить величину’ се остатка.
. Более удобной в этом отношении является формула (1), так как мы можем оценить величину’ се остатка.
Эта лекция взята со страницы онлайн помощи по математическому анализу:
Математический анализ онлайн помощь
Возможно эти страницы вам будут полезны:

