Перпендикулярность прямой и плоскости

Перпендикулярность прямой и плоскости

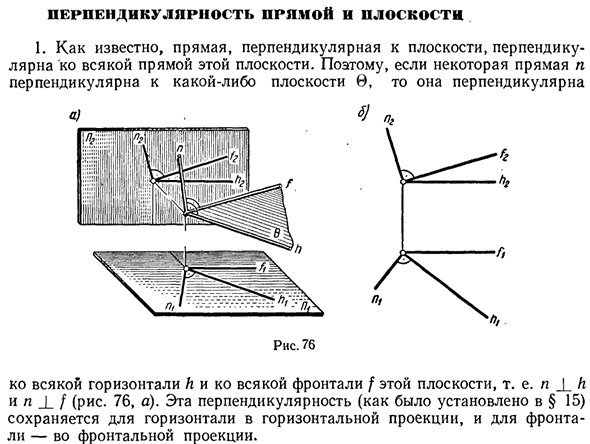
• Прямолинейность и плоскостность 1. Как вы знаете, линия, перпендикулярная плоскости, перпендикулярна любой линии в этой плоскости. Таким образом, если прямая l перпендикулярна какой-либо плоскости, она перпендикулярна. Рис. 76 Любая горизонтальная плоскость и любой фронт f в этой плоскости, т. Е. ЛL h и J J / (рис. 76, а).

• Эта вертикальность (установленная в §15) остается горизонтальной в горизонтальной проекции и фронтальной в передней проекции. Следовательно, проекции n {и n2 на плоскость n должны быть перпендикулярны плоскости в и удовлетворять следующему условию: «I -1_ n2 ± f2.

Где ht и / 2 — соответствующие проекции любого горизонтального h и фронта / плоскости © (рис. 76, б). Людмила Фирмаль

Обратное также верно: если горизонтальная проекция n линии n перпендикулярна горизонтальной проекции A горизонтальной h в конкретной плоскости, а фронтальная проекция n2 линии n перпендикулярна передней проекции плоскости / плоскости b / 2 Линия n и плоскость 0 перпендикулярны друг другу. На самом деле, из условия и n2_ | _ / 2, n ± h и Означает, что прямая n перпендикулярна двум прямым в плоскости 0.

В общем случае горизонталь h и фронт f любой плоскости являются пересекающимися прямыми. Следовательно, прямая линия l, перпендикулярная двум пересекающимся прямым линиям в плоскости 0, перпендикулярна самой плоскости. Исключением является плоскость проекции профиля, в которой горизонтальная и передняя грани параллельны друг другу. Линия, перпендикулярная такой плоскости, является линией профиля.

В этом случае перпендикулярность между линией и плоскостью определяется перпендикулярностью проекции профиля. Аналогично, прямые линии, которые перпендикулярны горизонтальной или передней плоскости проекции, являются горизонтальными или передней, соответственно, и вертикальность линии и плоскости задается в соответствии с вертикальностью горизонтальной или передней проекции.

Вот так Линия общего положения и плоскость перпендикулярны друг другу, только если проекция линии перпендикулярна одной и той же проекции соответствующей плоской линии уровня. То есть прямая горизонтальная проекция перпендикулярна горизонтальной горизонтальной проекции, а прямая фронтальная проекция перпендикулярна передней проекции.

• Если плоскость проецируется, линия, перпендикулярная ей, становится горизонтальной, и взаимная перпендикулярность между вырожденной проекцией плоскости и соответствующей проекцией линии сохраняется. 2. Рассмотрим пример создания прямой линии, перпендикулярной плоскости, и плоскости, перпендикулярной прямой. Пример 1.

Сначала настройте любой горизонтальный h и любой фронт / в плоскости, затем через проекцию точек A и A2 и через проекцию hi и / 2 вертикальную проекцию n tii, необходимую для плоскости 0 И нарисуйте n2 соответственно.

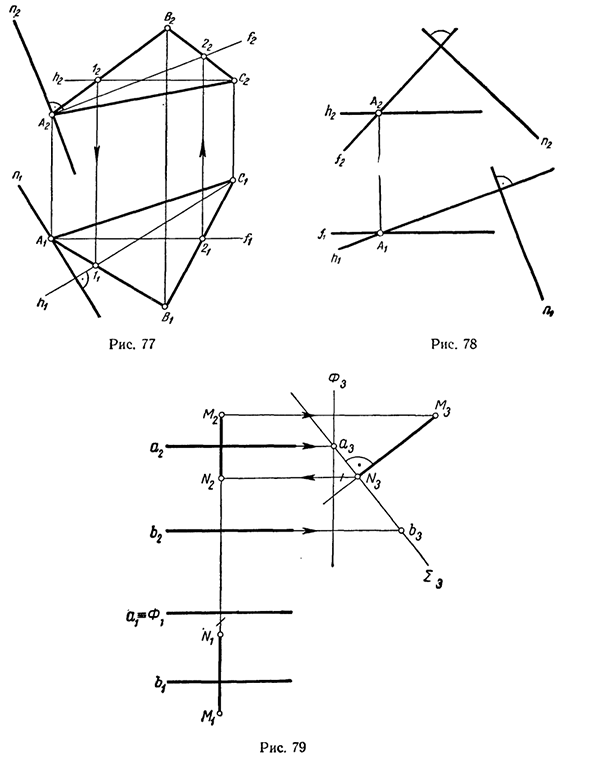
Нарисуйте прямую n перпендикулярно плоскости через точку A (A, B, C) на плоскости 0 (рисунок 77). Людмила Фирмаль

Если точка, которая рисует нормаль n на плоскости, находится вне плоскости, построение нормали выполняется в соответствии с условиями: ni ±, hl и я2 ] _ / 2. Кроме того, чтобы определить начало этого перпендикуляра на плоскости 0, необходимо создать пересечение линии n и плоскости 0. Пример 2. Нарисуйте плоскость ©, перпендикулярную указанной линии n через точку A (Рисунок 78).

Чтобы нарисовать горизонтальную точку h через точку A и фронт / вертикаль заданной линии n, вертикальное условие также должно включать f2 ± n2. Желаемая плоскость определяется двумя пересекающимися прямыми линиями: горизонтальной h и передней /. Пример 3. Естественный размер перпендикуляра, созданного из заданной точки M в плоскость проекции профиля 2 (a || b) (рис. 79).

В этом случае можно использовать сохранение перпендикулярности между вырожденной проекцией плоскости и соответствующей интересующей вертикальной проекцией. Уменьшенная проекция плоскости проекции профиля является проекцией профиля. Поэтому необходимо построить профильные проекции M3 и 2s для заданной точки M.ch на заданной плоскости 2. Связь.

Поскольку мы опустили вертикальную MZNZ от проекции M3 до проекции 23, мы можем видеть естественный размер вертикальной MN. Возвращаясь к системе проекционных плоскостей P и P2, вы получаете проекции MtNi и M2N2 нужного перпендикуляра.

Смотрите также:

Примеры решения задач по начертательной геометрии

Ортогональная проекция прямого угла	Взаимная перпендикулярность плоскостей
Прямые наибольшего уклона плоскости	Взаимная перпендикулярность прямых общего положения