Дифференциальным называется уравнение, связывающее независимую переменную 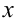 , неизвестную функцию
, неизвестную функцию 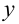 и производные неизвестной функции
и производные неизвестной функции 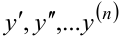 .
.
Общий вид дифференциального уравнения:

Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. Например, 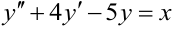 — это уравнение второго порядка;
— это уравнение второго порядка; 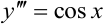 — уравнение третьего порядка.
— уравнение третьего порядка.
Решением дифференциального уравнения называется функция 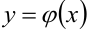 , которая, будучи подставлена в уравнение, обращает его в тождество. Например, если
, которая, будучи подставлена в уравнение, обращает его в тождество. Например, если 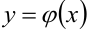 — решение уравнения (9.1), то
— решение уравнения (9.1), то
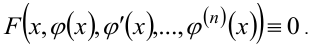
Если решение дифференциального уравнения содержит произвольные постоянные, оно называется общим решением. Частное решение дифференциального уравнения не содержит произвольных постоянных.
Методы исследования решений дифференциальных уравнений применяются при исследовании моделей реальных систем, зависящих от времени, например систем управления.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Градиент и его свойства |
| Экстремум функции двух переменных. Необходимые и достаточные условия экстремума |
| Дифференциальные уравнения первого порядка |
| Уравнения с разделяющимися переменными |
