Оглавление:
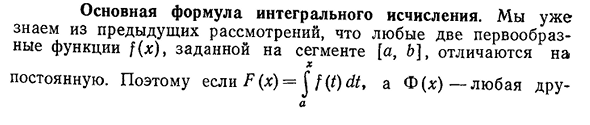


Основная формула интегрального исчисления.
- Основная формула для расчета интеграла. Из предыдущих соображений мы уже знаем, что две основные функции f (x), заданные сегменту[a,&], различны в X Это навсегда. (x)=J f (t) dt, а f (x) — это что-то
другое- Но integrals360CH. 9. Очистить Интеграл Римана Gaia-примитив непрерывной функции f (x), где f (x) — F (x)= Икс =C=const, т. е. f (x)=J f(t) dt+C (см. теорему 9.5). Положить в последнем
выражении первое х, тогда Х=Б.- Но В частности (см. пункт 1 предыдущего пункта), Людмила Фирмаль
любое J/(t) dt=Q Но Поскольку это функция, которая принимает конечное значение в точке a, b f (a)=C, f (B)=j/(x) dx+C. — Джей?(х)dх=Ф(б) — ф(а), Но Затем получается основное уравнение интегрального
исчисления. Сформулируем его в виде теоремы. Это позволяет повысить производительность вашего приложения. Чтобы вычислить определенный интеграл для отрезка непрерывной
- функции f (x) [a, 6], необходимо вычислить значение любого примитива в точках b и A и вычесть второе из первого. Теперь у нас есть правило для вычисления некоторого интеграла от интегрируемых функций широкого класса. Задача вычисления
определенного интеграла сводится к задаче получения примитивной непрерывной функции. Естественно, найти примитивные функции всех функций непросто. Мы уже неоднократно отмечали
функции, примитивы которых не представлены с точки зрения базовых функций (например, см. пункт 1 в этом пункте). В этом случае, Людмила Фирмаль
конечно, возникает вопрос о приближенном вычислении того или иного интеграла, о котором пойдет речь ниже. Основная формула Интеграла задается в виде p (x) yx=f (x)|®. Но Во многих случаях спецификация write F (x)|*=f(6) — f(a).
Смотрите также:

