Оглавление:
Определение непрерывности функции в точке и на отрезке
Пусть функция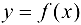 
определена на некотором множестве X.
Определение 4.1. Функция 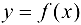называется непрерывной в точке 
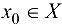, если она определена в некоторой окрестности точки 
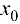и существует конечный предел
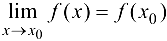
Пример 4.1.
Функция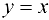 
непрерывна на всей числовой прямой.
Функция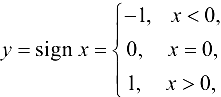 
, имеет разрыв в точке 
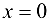, так как не существует 
.
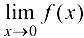Функция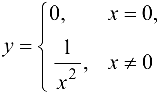 
имеет разрыв в точке 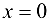, так как
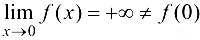
Определение 4.2 (по Коши). Функция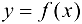 
называется непрерывной в точке 
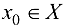, если она определена в некоторой окрестности точки 
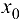и
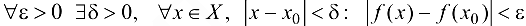
Определение 4.3 (по Гейне). Функция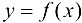 
называется непрерывной в точке 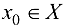, если она определена в некоторой окрестности точки 
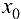и для любой последовательности 
, 
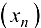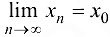, соответствующая последовательность значений функции сходится к числу 
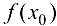, т. е. 
.
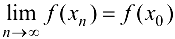Рассмотрим определение 4.1, согласно которому выполнено
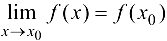
Тогда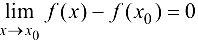 
. Внесем 
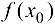под знак предела и учитывая, что 
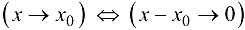, получим
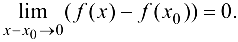
Разность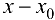 
называется приращением аргумента в точке 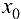и обозначается 
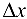, разность 
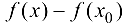называется приращением функции в точке 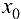, соответствующим приращению аргумента 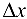, обозначается 
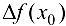или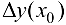 
. Тогда (4.1) можно представить в виде
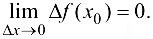
Определение 4.4. Функция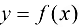 
называется непрерывной в точке 
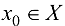, если она определена в некоторой окрестности точки 
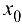и ее приращение в этой точке является бесконечно малой функцией при 
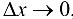, т. е. выполнено (4.2).
Определение 4.5. Функция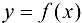 
называется непрерывной на отрезке 
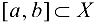, если она непрерывна во внутренних точках отрезка, а в граничных точках существуют односторонние пределы.
Заметим, что множество функций, непрерывных на отрезке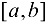 
принято обозначать 
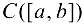, поэтому, если функция 
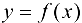непрерывна на отрезке 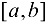, это можно показать следующим образом: 
.
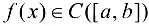Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
