Функция 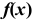 называется непрерывной в точке
называется непрерывной в точке 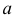 , если при
, если при 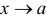 предел функции существует и равен ее частному значению в этой точке, т.е. если
предел функции существует и равен ее частному значению в этой точке, т.е. если
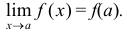
Этому определению равносильно следующее:
Функция 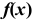 называется непрерывной в точке
называется непрерывной в точке 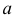 , если в этой точке бесконечно малому приращению аргумента
, если в этой точке бесконечно малому приращению аргумента 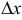 соответствует бесконечно малое приращение функции
соответствует бесконечно малое приращение функции 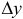 , т.е. если
, т.е. если 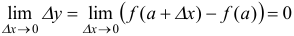 .
.
Функция 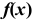 разрывна в точке
разрывна в точке 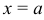 : 1) если не существует
: 1) если не существует 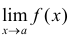 , или 2) функция
, или 2) функция 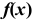 не определена в точке
не определена в точке 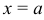 , или 3) существует
, или 3) существует 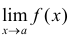 , но он не равен значению функции в этой точке, т.е.
, но он не равен значению функции в этой точке, т.е. 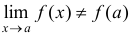 .
.
Для того чтобы функция 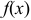 была непрерывной в точке
была непрерывной в точке 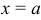 , необходимо и достаточно, чтобы выполнялись условия:
, необходимо и достаточно, чтобы выполнялись условия:
функция должна быть определена в некоторой 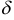 — окрестности точки
— окрестности точки 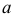 и в самой точке
и в самой точке 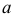 ;
;
функция должна иметь одинаковые односторонние пределы, т.е.
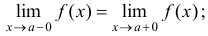
односторонние пределы должны быть равны 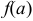 .
.
Если существует конечный 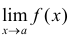 , но
, но 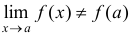 , то точка
, то точка 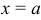 называется точкой устранимого разрыва функции.
называется точкой устранимого разрыва функции.
Точка 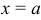 называется точкой разрыва 1-го рода для
называется точкой разрыва 1-го рода для 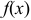 , если существуют конечные односторонние пределы функции
, если существуют конечные односторонние пределы функции 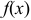 в точке
в точке 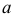 и
и
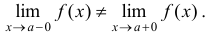
В противном случае имеем точку разрыва 2-го рода.
Скачком функции 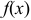 в точке а называется разность ее односторонних пределов
в точке а называется разность ее односторонних пределов 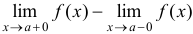 , если они различны.
, если они различны.
В случае 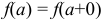 функция
функция 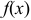 непрерывна справа в точке
непрерывна справа в точке 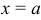 .
.
В случае 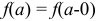 функция
функция 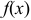 непрерывна слева в точке
непрерывна слева в точке 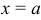 .
.
Функция 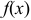 непрерывна в точке
непрерывна в точке 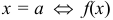 непрерывна в этой точке слева и справа.
непрерывна в этой точке слева и справа.
Если 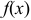 и
и 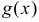 непрерывны в точке
непрерывны в точке 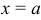 , то
, то 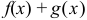 и
и 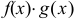 непрерывны в этой точке;
непрерывны в этой точке; 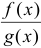 непрерывна в точке
непрерывна в точке 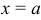 , если
, если 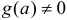 .
.
Функция называется непрерывной в интервале, если она непрерывна во всех точках этого интервала.
Любая элементарная функция непрерывна в области определения.
Пример:
Задана функция 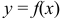 . Найти точки разрыва функции, если они существуют. Сделать чертеж.
. Найти точки разрыва функции, если они существуют. Сделать чертеж.
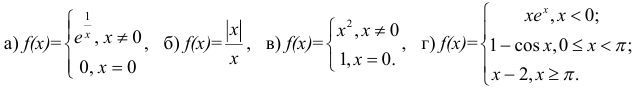
Решение:
а) При 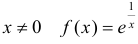 непрерывна при
непрерывна при 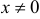 . Рассмотрим т.
. Рассмотрим т. 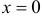 . Вычислим
. Вычислим 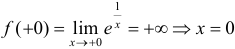 — точка разрыва 2-го рода.
— точка разрыва 2-го рода. 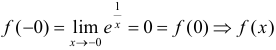 непрерывна слева в точке
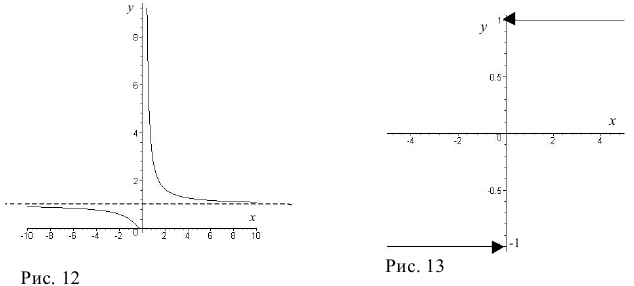
непрерывна слева в точке 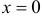 . График функции
. График функции 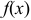 изображен на рис. 12.
изображен на рис. 12.
б) Функция 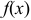 определена при всех значениях
определена при всех значениях 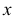 , кроме
, кроме 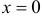
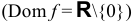 . Следовательно,
. Следовательно, 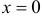 — точка разрыва. Исследуем ее характер.
— точка разрыва. Исследуем ее характер.
Вычислим
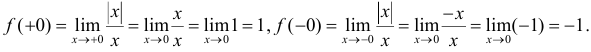
Так как 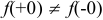 , но
, но 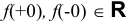 , то
, то 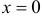 — точка неустранимого разрыва 1 -го рода. При
— точка неустранимого разрыва 1 -го рода. При 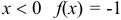 , при
, при 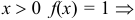 при
при 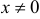
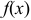 непрерывна. График функции
непрерывна. График функции 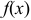 изображен на рис. 13.
изображен на рис. 13.
в) При 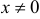
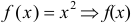 непрерывна в т.
непрерывна в т. 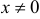 .
.
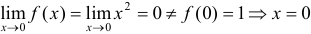 — точка устранимого разрыва.
— точка устранимого разрыва.
Рассмотрев 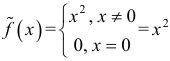 , т.е. изменив значение
, т.е. изменив значение 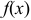 в точке
в точке
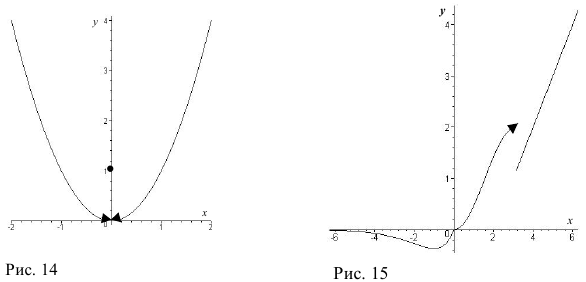
разрыва, получаем непрерывную функцию. График функции 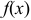 изображен на рис. 14.
изображен на рис. 14.
г) Поскольку элементарные функции 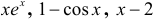 непрерывны на
непрерывны на 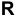 , то точками разрыва могут быть лишь
, то точками разрыва могут быть лишь 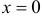 и
и 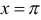 . Имеем
. Имеем
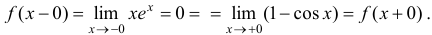
Значит, в точке 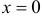 функция
функция 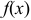 непрерывна. Аналогично,
непрерывна. Аналогично, 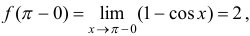
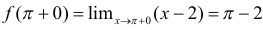 . Тогда в точке
. Тогда в точке 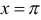 функция имеет разрыв первого рода с величиной скачка
функция имеет разрыв первого рода с величиной скачка 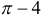 . График функции
. График функции 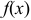 изображен на рис 15 .
изображен на рис 15 .
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:

